prof. dr hab. Feliks Wysocki

katedra finansów i rachunkowości,

pokój 506.

Literatura przedmiotu.

1. Wprowadzenie do ekonometrii w przykładach i zadaniach, 1996, 2004, red. nauk. K. Kukuła, wydawnictwo naukowe PWN, Warszawa,

2. Badania operacyjne w przykładach i zadaniach, 2004, red. nauk. K. Kukuła, wydawnictwo naukowe PWN, Warszawa 1996,

3. Guzik B., Jurek W., 1997, Ćwiczenia z ekonometrii, wyd. Akademii Ekonomicznej w Poznaniu, Poznań,

4. Guzik B., Jurek W., 1996, Ekonometria z zadaniami, wyd. Akademii Ekonomicznej w Poznaniu, Poznań,

5. Borkowski B., Dudek H., Szczęsny W., 2003, Ekonometria wybrane zagadnienia, wydawnictwo naukowe PWN, Warszawa,

6. Dorosiewicz i in., 1996, Ekonometria, Wydawnictwo Szkoły Głównej Handlowej, Warszawa,

7. Welfe A., 2003, Ekonometria. Metody i zastosowanie, PWE, Warszawa,

8. Maddala G. S., 2006, Ekonometria, wydawnictwo naukowe PWN, Warszawa.

Plan wykładów i ćwiczeń (program nauczania).

1. Ogólna definicja Ekonometrii,

2. Pojęcie modelu ekonomiczno - matematycznego,

3. Dwie klasy modeli ekonomiczno - matematycznych:

- modele ekonometryczne

- modele optymalizacyjne (decyzyjne lub programowania matematycznego),

4. Podstawowe obszary badawcze ekonometrii,

5. Przykłady oszacowanych modeli ekonomiczno - matematycznych według poszczególnych obszarów badawczych ekonometrii,

6. Klasyfikacja modeli ekonometrycznych według różnych kryteriów,

7. Etapy budowy modelu ekonometrycznego:

- sformułowanie ogólnej postaci modelu,

- zgromadzenie danych empirycznych (statystycznych), wykorzystanych do oszacowania parametrów modelu (strukturalnych i struktury stochastycznej),

- ustalenie analitycznej postaci modelu,

- estymacja parametrów strukturalnych modelu,

- weryfikacja merytoryczna i statystyczna modelu,

- praktyczne wykorzystanie modelu,

8. Zasady budowy wybranych typów modeli ekonometrycznych liniowych i nieliniowych,

9. Zastosowanie metod ekonometrycznych do modelowania procesów ekonomicznych (analizy procesów produkcyjnych i popytu konsumpcyjnego),

10. Zasady budowy modeli wielorównaniowych,

11. Zasady konstrukcji modeli optymalizacyjnych (modele liniowe),

12. Zagadnienie rozwiązywania modeli programowania liniowego,

13. Dualność w programowaniu liniowym, reguły tworzenia programów dualnych,

14. Zagadnienie transportowe i metody jego rozwiązywania,

15. Niektóre nieliniowe zagadnienia optymalizacyjne.

1. Ogólna definicja ekonometrii.

Ekonometria zajmuje się ogólną weryfikacją empiryczną praw ekonomicznych, czyli szacowaniem związków ilościowych występujących pomiędzy badanymi zjawiskami na podstawie dostępnych danych statystycznych nie eksperymentalnych.

Charakterystyka danych empirycznych.

Dane nie eksperymentalne.

Pochodzą z życia gospodarczego. Źródłem tych danych są roczniki statystyczne, dane sprawozdawcze firm, raporty, dane z wyników badań ankietowych itd. Uzyskiwane są tylko raz. Posługujemy się nimi w naukach ekonomicznych i humanistycznych.

Dane eksperymentalne.

Pochodzą ze świata przyrody. Źródłem tych danych są doświadczenia i eksperymenty przyrodnicze prowadzone w laboratoriach i na poletkach doświadczalnych. Mogą być uzyskiwane wielokrotnie. Posługujemy się nimi w naukach przyrodniczych.

Ekonometria jest:

1. Nauką stosowania metod matematycznych i statystycznych do mierzenia relacji ekonomicznych,

2. Narzędziem empirycznej weryfikacji praw ekonomicznych formułowanych na gruncie ekonomii -

mikro i makroekonomii,

3. Prawa, które formułuje się na gruncie mikro i makroekonomii:

- popyt na dany produkt zależy od dochodów gospodarstw domowych i ceny,

- wielkość produkcji zależy od nakładów czynników produkcji (kapitału i pracy),

- koszty jednostkowe zależą od skali produkcji,

- wraz ze wzrostem dochodów gospodarstw domowych udział dochodów przeznaczonych na zakup artykułów żywnościowych (żywność) ulega zmniejszeniu (prawo Engla).

2. Pojęcie modelu ekonomiczno - matematycznego.

Związki ilościowe, które zachodzą między zjawiskami gospodarczymi ujmuje się w postaci tak zwanego modelu ekonomiczno - matematycznego.

Model ekonomiczno - matematyczny jest to uproszczone odwzorowanie za pomocą formuł matematycznych (równań i nierówności liniowych i nieliniowych), związków ilościowych zachodzących między zjawiskami gospodarczymi w badanym fragmencie rzeczywistości gospodarczej.

Ekonometria zajmuje się tworzeniem i weryfikacją modeli ekonomiczno - matematycznych.

Klasy modeli matematyczno - ekonomicznych.

Modele ekonometryczne (ekonomiczno - matematyczne):

1. Modele ekonometrii klasycznej:

- jednorównaniowe (liniowe, nieliniowe),

- wielorównaniowe.

2. Modele optymalizacyjne (decyzyjne), programowania matematycznego:

- modele badań operacyjnych.

Co to jest model ekonometryczny ?

Jest to równanie, bądź układ równań i służy do opisu zasad i relacji związków ilościowych. Występuje pomiędzy zjawiskami gospodarczymi w badanym momencie rzeczywistości gospodarczej.

Model ekonometryczny jest konstruowany na podstawie danych statystycznych nie eksperymentalnych. Zbudowane modele ekonometryczne mogą być wykorzystane w następujących obszarach:

1. Do diagnozowania sytuacji gospodarczej,

2. Prognozowanie przyszłego stanu zjawisk gospodarczych,

3. Przeprowadzanie rachunków symulacyjnych.

Diagnostyka jest to analiza związków ilościowych zachodzących między zjawiskami gospodarczymi w przeszłości.

Prognozowanie to przewidywanie przyszłego stanu zjawisk gospodarczych. Co będzie ?

Przeprowadzanie rachunków symulacyjnych. Symulacja to wykonywanie zabiegów, które ma na celu dać odpowiedź na pytanie jak zachowałby się obiekt (przedsiębiorstwo, gospodarstwo domowe, jednostka administracyjna, człowiek na stanowisku pracy) opisany danym modelem ekonometrycznym w określonych założeniach. Co byłoby gdyby ?

Modele optymalizacyjne w sensie naturalnym to są układy równań liniowych i nieliniowych i służą do planowania działalności gospodarczej. Co powinno być ?

Planowanie to ustalenie celów gospodarczych i znajdowanie najlepszych rozwiązań ekonomicznych lub gospodarczych, które prowadzą do osiągnięcia postawionych celów gospodarczych.

Produktem planowania jest plan gospodarczy czyli program działań, który należy wprowadzić w życie, aby osiągnąć dany cel gospodarczy. Są to szczególnie klasy modeli optymalizacyjnych, które są stosowane przy podejmowaniu decyzji w przedsiębiorstwie. np. planowanie dotyczące zapasów, harmonogramu.

Model ekonometryczny (ekonometrii klasycznej) - konstrukcja formalna, która za pomocą równania lub układu równań przedstawia zasadnicze powiązania, związki ilościowe występujące pomiędzy zjawiskami gospodarczymi w badanym fragmencie rzeczywistości gospodarczej na podstawie dostępnych danych nie eksperymentalnych.

Ogólna postać modelu ekonometrycznego w zapisie formalnym:

y = f(X1, X2,…,Xk,β0,β1,…,βk,e)

Model ekonometryczny jest oparty na związkach przyczynowo - skutkowych, skutkach zjawisk gospodarczych.

Zmienne y to zmienne skutek, zmienne objaśniane lub zmienne zależne.

Zmienne występują po lewej stronie równania i wyrażają zjawiska ekonomiczne wyjaśniane przez model. np. wielkość produkcji, udział wydatków.

f(X1, X2,…,Xk) te zmienne wyrażają zjawiska ekonomiczne wpływające na zjawiska objaśniane na zmienną y. I zmienne te określamy mianem zmiennych objaśniających lub zmienne niezależne

Popyt - ceny i dochody gospodarstw domowych,

Koszty produkcji jednostkowej - skala produkcji,

Nakłady czynników produkcji.

β1,…,βk to parametry strukturalne modelu, niewiadome. Po zbudowaniu modelu uzyskujemy ich oceny, które wyrażają siłę i kierunek oddziaływania zmiennych objaśniających na zmienną objaśnianą.

β1 określa siłę i kierunek oddziaływania zmiennej X1 na zmienną X2.

β0 jest szczególnym parametrem strukturalnym, i stałą równania modelu.

e to składnik losowy modelu. Wyraża łączny efekt oddziaływania na zmienną objaśnianą tych wszystkich czynników ubocznych i przypadkowych, które nie zostały uwzględnione w modelu jako przyczyny główne postaci zmiennych.

f określa typ zależności pomiędzy zmienną y oraz X1, X2,…Xk i jest to typ zależności funkcyjnej.

np. funkcje liniowe, kwadratowe, potęgowe, wykładnicze, logistyczne, logitowe, hiperboliczne.

Założenia, które przyjmuje się przy budowie modelu:

1. Zjawiska ekonomiczne wyrażone w postaci zmiennej objaśnianej i objaśniających muszą być kwantyfikowalne (można je wyrazić w postaci ilościowej za pomocą wartości liczbowych).

2. Wartości liczbowe zmiennych objaśniających i objaśnianej dla badanych obiektów muszą być dostępne.

3. Wartości parametrów strukturalnych β0,β1,…,βk szacuje się na podstawie danych nie eksperymentalnych dotyczących kształtowania się zmiennej objaśnianej i zmiennych objaśniających w przeszłości dla badanych obiektów - jednostek czasowych lub przestrzennych.

W wyniku oszacowania modelu uzyskujemy wartości parametrów strukturalnych, które noszą nazwę ocen. Oznaczamy je odpowiednio b0, b1,…,bk. W wyniku oszacowania modelu uzyskujemy również wartości składnika losowego i określamy je mianem resztami modelu i oznaczmy
, n czyli tyle ile występuje w modelu badanym.

Postać ogólna modelu ekonometrycznego w ujęciu macierzowym:

Ogólną postać modelu ekonometrycznego w ujęciu macierzowym można przedstawić następująco:

y = f(X, β, e)

gdzie:

y - wektor zaobserwowanych wartości zmiennej objaśnianej, przedstawia dane statystyczne pochodzące z n jednostek statystycznych dotyczące kształtowania się wartości zmiennej objaśnianej w przeszłości.

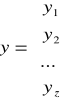
Obiekty - jednostki gospodarcze np. gospodarstwa domowe, jednostki przestrzenne - gminy, powiaty, jednostki czasowe.

y₁ - zaobserwowana wartość zmiennej objaśnianej w obiekcie o numerze pierwszym.

Wektor zaobserwowanej wartości zmiennej objaśnianej musi mieć wartości znane.

X - macierz zaobserwowanych wartości zmiennych objaśniających, przedstawia dane statystyczne dotyczące zaobserwowanych wartości zmiennych objaśniających X₁,X₂,…,X_k w n jednostkach statystycznych.

zmienne objaśniające

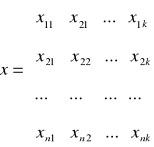
jednostki statystyczne

β - wektor niewiadomych parametrów strukturalnych.

β =

e - wektor wartości składnika losowego.

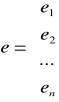
Parametr β - w wyniku oszacowania modelu uzyskujemy wartości parametrów strukturalnych modelu, które oznaczają odpowiednio β₁, β_2, β_k. Są to oceny i są wartościami nieznanymi. Po oszacowaniu uzyskujemy wartości liczbowe.

Parametr β₁ - przy parametrze występuje zmienna objaśniająca, której wartość tożsamościowa równa się jeden.

Parametr e - określa wpływ zmiennych, które nie zostały w modelu potraktowane jako czynniki dodatkowe, poboczne, przypadkowe. Parametrów e jest tyle ile jest obiektów.

W wyniku oszacowania modelu ekonometrycznego uzyskujemy oszacowane wartości składnika losowego, które określamy mianem reszt modelu (n).

Ekonometria jako nauka interdyscyplinarna (nauki wspomagające ekonometrię).

- ekonomia,

- matematyka,

- statystyka opisowa i matematyczna,

- informatyka.

Ekonomia dostarcza informacji na temat badanych zjawisk i od tego zjawiska czynników odkształceń.

Matematyka. Matematykę wykorzystuje się do konstrukcji modelu. Z metod matematycznych korzystamy w etapie konstrukcji modelu.

Statystyka opisowa i matematyczna służy przede wszystkim do weryfikacji modelu, czyli sprawdzenia poprawności i estymacji jakości modelu.

Informatyka - metody informatyczne wykorzystuje się do gromadzenia danych na elektronicznych nośnikach informatycznych i rozwiązywania modeli ekonometrycznych.

Przykłady zapisu ogólnego modelu ekonometrycznego:

Model opisujący kształtowanie się popytu na masło w 10 gospodarstwach domowych w zależności od poziomu dochodów gospodarstw domowych i przeciętnej liczby osób w rodzinie - gospodarstwie domowym.

W zapisie formalnym model przyjmuje postać ogólną:

y = f(D, LO, β₀, β₁,β₂, e)

W modelu ogólnym przyjęto zmienne:

y - przeciętny miesięczny wydatek na masło przypadający na jedną osobę w gospodarstwie domowym (w zł/m-c/os) lub przeciętne miesięczne spożycie masła przypadające na jedną osobę w gospodarstwie domowym (w kg/m-c/os).

D - przeciętny miesięczny dochód rozporządzalny przypadający na jedną osobę w gospodarstwie domowym (w zł/m-c/os).

LO - liczba osób ekwiwalentnych w gospodarstwie domowym (w jednostkach przeliczeniowych - ekwiwalentnych).

β₁,β₂ - parametry strukturalne modelu, które określają siłę i kierunek oddziaływania zmiennych objaśniających na zmienną objaśnianą.

β₀ - stała równia modelu.

e - pozostałe zjawiska - czynniki, które mogą wywierać wpływ na zmienną objaśnianą y, a które nie zostały w modelu uwzględnione jako przyczyny główne.

W zapisie macierzowym model przyjmuje postać ogólną:

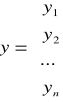
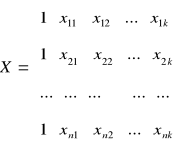
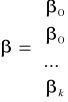
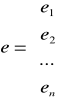
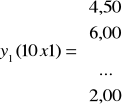
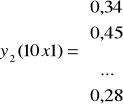
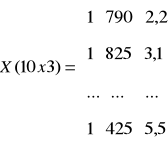
4,50 - wydatki na masło (na os/m-c),

0,34 - oszacowane spożycie masła na osobę (w m-c/na os),

Kolumna 1 - wyraz wolny, stała równania modelu,

X₁, 790 - przeciętne dochody (na os/na m-c),

2,2 - średnia przeciętna liczba osób w rodzinie.

W wyniku budowy modelu uzyskujemy dane parametry strukturalne modelu, które wpływ dochodów gospodarstwa domowego oraz wpływ liczby osób w rodzinie na kształtowanie się popytu na masło.

Podstawowe obszary badawcze ekonometrii:

1. Wykrywanie ilościowych prawidłowości zachodzących pomiędzy zjawiskami gospodarczymi i symulacja zachowań obiektów gospodarczych za pomocą zbudowanych modeli ekonometrycznych.

2. Wykrywanie tendencji rozwojowych zjawisk gospodarczych, czyli opis kształtowania się zjawisk gospodarczych w czasie.

3. Prognozowanie, czyli przewidywanie przyszłego stanu zjawisk gospodarczych na podstawie zbudowanych modeli ekonometrycznych przyczynowo - skutkowych i modeli tendencji rozwojowych.

4. Optymalizacja decyzji gospodarczych, czyli poszukiwanie optymalnych planów produkcji w skali mikroekonomicznej, mezoekonomicznej i makroekonomicznej.

1. Wykrywanie ilościowych prawidłowości zachodzących pomiędzy zjawiskami gospodarczymi oraz symulacja zachowań obiektów gospodarczych.

Przykład 1.

Model ekonometryczny liniowy z dwiema zmiennymi objaśniającymi.

Model ekonometryczny opisujący kształtowanie się kosztów ogólnych produkcji nasion ozdobnych

(w tys. zł.) w zależności od produkcji nasion (w setkach ton) oraz od wielkości zatrudnienia

(w osobach) w przedsiębiorstwie „Siewca” oszacowany na podstawie danych sprawozdawczych pochodzących z 10 lat.

Etap 1.

Definiujemy zmienną objaśnianą i zmienne objaśniające i definiujemy obiekty gospodarcze

(jednostki czasowe).

y zmienna objaśniana - koszty ogólne produkcji nasion ozdobnych (w tys. zł).

Potencjalne zmienne objaśniające:

X1 - wielkość produkcji nasion (w setkach ton).

X2 - wielkość zatrudnienia w osobach.

Definiujemy obiekty badane - 10, (n = 10).

Stawiamy problem badawczy.

Celem badawczym jest określenie siły i kierunku oddziaływania wielkości produkcji i zatrudnienia w przedsiębiorstwie „Siewca” na kształtowanie się kosztów produkcji w przedsiębiorstwie.

Etap 2.

Gromadzi się dane statystyczne, które będą stanowiły podstawę oszacowania parametrów strukturalnych i parametrów struktury stochastycznej (są to parametry służące do oceny stopnia dopasowania modelu do danych empirycznych).

Dane zapisujemy w postaci macierzowej, w postaci wektora zaobserwowanych wartości y - zmiennej objaśnianej i w postaci macierzy zaobserwowanych wartości.

Koszty produkcji w tys. zł (Y), wielkość produkcji w setkach ton (X1), oraz wielkość zatrudnienia w osobach (X2) w przedsiębiorstwie „Siewca”.

Lata	Koszty produkcji w tys. zł. Y1	Wielkość produkcji (setki ton) X1	Zatrudnienie (osoby) X2
1	34911	10	60
2	35123	11	72
3	35642	11	83
4	35015	9	85
5	36395	12	91
6	36521	11	102
7	36314	12	111
8	37692	13	123
9	37612	14	125
10	37158	13	127

Estymacja parametrów strukturalnych modelu, która służy do oszacowania modelu liniowego w taki sposób aby suma najniższych kwadratów odchyleń wartości empirycznych zmiennej objaśnianej była minimalna.

Oszacowany model przyjął następującą postać:

(R²) = 94%

Symulacja zachowań przedsiębiorstwa „Siewca” za pomocą zbudowanego modelu ekonometrycznego.

Wykorzystując zbudowany model określić wielkość produkcji przy założeniu, że:

- koszty produkcji wyniosą 37 mln zł,

- liczba osób zatrudnionych wyniesie 120.

Mamy:

37000 = 30177,44 + 309,38 ∙ X₁ + 25,26 ∙ 120

3791,4 = 309,38 X₁

X₁ = 1225 ton

Konkluzje.

Ocena parametru b1. Pierwszy parametr występujący przy zmiennej X1informuje, że przy założeniu stałej liczby osób zatrudnionych w przedsiębiorstwie (X2 jest Konstans) wzrost wielkości produkcji nasion o 100 t powodował wzrost kosztów ogólnych produkcji nasion przeciętnie o 309,4 tys. zł.

Ocena parametru b2. Parametr występujący przy zmiennej objaśnianej (X2) informuje, że przy założeniu stałej wielkości produkcji (X1) wzrost liczby pracowników w przedsiębiorstwie o jedną osobę powodował wzrost kosztów produkcji o 25 260 zł w ciągu roku.

Jest to teoretyczna wartość zmiennej objaśnianej (koszty produkcji) przy założeniu, że X1 i X2 równają się zero.

R² to współczynnik determinacji. Określa, w jakim stopniu zmienność całkowita zmiennej objaśnianej została wyjaśniona przez model. Przyjmuje wartości od 0 do 100 %.

Wykorzystanie modelu służy do wykonywania rachunków symulacyjnych. Co by było gdyby ?

Przykład 2.

Model potęgowy z wieloma zmiennymi objaśniającymi.

Model ekonometryczny opisujący kształtowanie się produkcji globalnej w tys. zł/ gospodarstwo w zależności od nakładów czynników produkcji w zbiorowości 204 gospodarstw z makroregionu środkowo - zachodniego. W wyniku estymacji uzyskano następujący model ekonometryczny:

nakziem^0,229 nakprac^0,131 nakobrot^0,469 amort^0,103obw^0,199

gdzie:

zmienna objaśniana:

prodglob - produkcja globalna z gospodarstwa w tys. zł,

zmienne objaśniające:

nakziem - nakłady ziemi w tys. zł na gospodarstwo,

nakprac - nakłady pracy w tys. zł na gospodarstwo,

nakobrot - nakłady środków obrotowych w tys. zł na gospodarstwo,

amort - amortyzacja (część wartości środków trwałych przeniesiona na wytwarzane produkty) w tys. zł na gospodarstwo,

obw - obrót wewnętrzny w tys. zł na gospodarstwo (zużycie produktów wyprodukowanych w gospodarstwie na potrzeby produkcyjne gospodarstw).

Oszacowane oceny parametrów strukturalnych modelu, które w modelu potęgowym noszą nazwę współczynników elastyczności produkcji względem czynników produkcji.

Współczynnik elastyczności pokazuje o ile procent zmieni się wartość zmiennej objaśnianej, jeżeli wartość zmiennej objaśniającej wzrasta o 1%. Współczynnik elastyczności przy zmiennej objaśnianej β₃ = 0,469 pokazuje, że wzrost nakładów środków obrotowych o 1% przyczyniał się do wzrostu produkcji globalnej zbiorowości 204 gospodarstw rolnych przeciętnie o 0,47%.

Produkcja globalna najsilniej reagowała na zmiany nakładów środków obrotowych.

Suma ocen parametrów strukturalnych (współczynników elastyczności) w modelu potęgowym, który jest funkcją produkcji określa stopień proporcjonalności wzrostu produkcji względem wzrostu nakładów.

Badanie ocen sumy parametrów strukturalnych (współczynników elastyczności).

Mogą zachodzić trzy sytuacje:

- jeżeli
, to produkcja wzrastała w badanym okresie w tempie szybszym, aniżeli nakłady ponoszone na produkcję - przypadek rosnącej wydajności produkcji,

- jeżeli
, to produkcja wzrastała w mniejszym tempie niż nakłady - przypadek malejącej wydajności produkcji.

0,229 + 0,131 + 0,469 + 0,101 + 0,199 = 1,129 > 1

Wnioski:

Produkcja globalna w badanych gospodarstwach rosła więcej niż proporcjonalnie w stosunku do nakładów ponoszonych na tę produkcję. Zatem świadczy to o rosnącej wydajności produkcji zbiorowości 204 gospodarstw indywidualnych.

K - liczba zmiennych objaśnianych w modelu,

y - liczba zmiennych objaśniających.

Wykrywanie tendencji rozwojowych zjawisk gospodarczych.

Postać ogólna modelu tendencji rozwojowej, czyli trendu:

y = f(t, e)

gdzie:

y - zjawisko wyjaśniane przez model, którego rozwój w czasie jest analizowany za pomocą modelu ekonometrycznego,

t - zmienna objaśniająca - czasowa, która w kolejnych latach lub momentach czasowych przyjmuje wartości:

t = 1, w I okresie,

t = 2, w II okresie,

… , …,

t = n, w n - tym okresie.

e - składnik losowy modelu, który przedstawia tę część zmienności całkowitej zmiennej objaśnianej, która nie została wyjaśniona przez model, czyli wprowadzoną do modelu zmienną czasową.

f - oznacza określony typ zależności występujący pomiędzy zmienną objaśnianą a zmienną objaśniającą.

W typowaniu dynamiki zjawisk (tendencji rozwojowych) stosuje się następujące typy modeli:

- model liniowy, model wykładniczy, model logistyczny, model wielomianowy stopnia drugiego, nie stosuje się modelu potęgowego.

Przykład 3.

Dwa modele opisujące tendencje rozwojowe liczby indywidualnych gospodarstw (tys. gosp.) w dwóch grupach obszarowych.

1⁰ 10 - 15 ha UR,

2⁰ pow. 15 ha UR.

W Polsce w latach 1986 - 1998.

Uzyskano dwa modele tendencji rozwojowej o następującej postaci:

lig 10 - 15

lig 15 i więcej

Określają liczby gospodarstw indywidualnych w Polsce (w tys.) w grupach obszarowych odpowiednio 10 - 15 ha i powyżej 15 ha użytków rolnych w latach 1986 - 1998.

t - zmienna objaśniająca czasowa, która w kolejnych latach przyjmuje wartości:

1986 = 1

1987 = 2

…

1998 = 13.

Oceny b₁ mogą posłużyć do obliczenia średniorocznego tempa zmian wartości zmiennej objaśnianej w analizowanym okresie. Średnioroczne tempo zmian:

r = (b₁ - 1) 100%

wynosi:

r₁₀ - ₁₅ = (0,9756 - 1) 100% = - 2,44 %

r₁₅ = (1,0259 - 1) 100% = 2,59 %

Z obliczeń wynika, że w latach 1986 - 1998 liczba gospodarstw powyżej 15 ha wzrastała średniorocznie o 2,59% natomiast w tym okresie malała liczba gospodarstw obszarowo mniejszych (z grupy obszarowej 10 - 15 ha) przeciętnie o 2,44%.

Prognozowanie zjawisk gospodarczych na podstawie oszacowanych modeli ekonometrycznych.

Prognozowanie czyli przewidywanie przyszłego stanu zjawisk gospodarczych.

Przykład 4.

W odniesieniu do poprzedniego zadania.

Sporządzić prognozę liczby gospodarstw o powierzchni powyżej 15 ha UR na rok 1999 (t = 14).

- realizacja zmiennej y w roku 1999.

Błąd prognozy expost:

tys. gosp.

Względny błąd prognozy (WBP _expost).

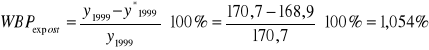
Modele ekonometrii klasycznej można dzielić z punktu widzenia różnych kryteriów typologicznych.

Walory poznawcze modelu:

- modele przyczynowo - skutkowe,

- modele tendencji rozwojowej.

Rola czynnika czasu w modelu:

- dynamiczne (powiązania między zmienną występującą w różnych okresach, jak również występuje zmienna czasowa), są szacowane na podstawie szeregów dynamicznych albo danych przekrojowo - czasowych pochodzących przynajmniej z dwóch okresów,

- statystyczne.

Postać analityczna równania modelu:

- liniowa

- potęgowa

- wykładnicza

- potęgowa - wykładnicza

- wielomianowa stopnia drugiego

Liczba zmiennych objaśniających w modelu:

- modele jednorównaniowe (niewiadoma stoi po lewej stronie równania),

- modele wielorównaniowe o równaniach współzależnych (układy równań), zbudowane dla jednej zmiennej objaśnianej, dana zmienna objaśniana może pełnić rolę zmiennej objaśniającej w innym równaniu.

Etapy budowy modelu ekonometrycznego.

Budowa modelu ekonometrycznego jest procesem wieloetapowym, złożonym w, którym można wyróżnić 6 podstawowych etapów.

1. Merytoryczna analiza zjawiska i stosownie do tego zdefiniowanie zmiennej objaśnianej, zmiennych objaśniających oraz jednostek statystycznych.

2. Zebranie danych statystycznych dotyczących kształtowania się zmiennej objaśnianej i zmiennych objaśniających w przeszłości.

3. Ustalenie postaci analitycznej równania modelu czyli typu zależności występujących pomiędzy zmienną objaśnianą a zmiennymi objaśniającymi.

4. Dokonanie estymacji parametrów strukturalnych modelu, najczęściej metodą najmniejszych kwadratów.

5. Badanie jakości modelu:

- weryfikacja merytoryczna, polegająca na interpretacji ekonomicznej ocen parametrów strukturalnych,

- weryfikacja statystyczna za pomocą analizy wariancji zmiennej objaśnianej i analizy ocen parametrów struktury stochastycznej modelu.

6. Wykorzystanie modelu do analizy zależności występujących pomiędzy badanymi zjawiskami w przeszłości, do prognozowania, czyli przewidywania przyszłego stanu zjawisk gospodarczych oraz analiz symulacyjnych.

Etap 1.

Sprecyzowanie zmierzenia (problemu) badawczego, wybór potencjalnych zmiennych objaśniających w oparciu o:

- posiadane doświadczenie tzn. intuicję badawczą,

- znajomości procesów gospodarczych w badanej dziedzinie zjawisk.

Zdefiniowanie jednostek statystycznych, którymi w zależności od celu badania mogą być jednostki (obiekty):

- gospodarcze,

- przestrzenne,

- czasowe,

- mieszane (gospodarczo - czasowe, przestrzenno - czasowe).

Etap 2.

Zgromadzenie danych ekonomiczno - empirycznych, które zostaną wykorzystane do estymacji i weryfikacji modelu.

Wykorzystane dane można klasyfikować według dwóch kryteriów:

1. Źródła pochodzenia danych:

a) dane pierwotne,

b) dane wtórne.

2. Czasu:

a) dane przekrojowe,

b) dane dynamiczne,

c) dane mieszane (przekrojowo - dynamiczne).

Dane przekrojowe - pochodzą z jednego zbioru jednostek statystycznych rozpatrywanych w danym momencie lub okresie.

Dane dynamiczne - pochodzą z jednego obiektu gospodarczego, rozpatrywane w kolejnych jednostkach czasowych.

Dane przekrojowo - dynamiczne - dane przekrojowe, które pochodzą z kilku, ale przynajmniej dwóch okresów.

Zapisujemy w postaci macierzowej, czyli w postaci wektora zaobserwowanej wartości zmiennej objaśniającej y, w postaci macierzy X zaobserwowanych wartości zmiennych objaśnianych.

Etap 3.

Ustalenie postaci analitycznej równania modelu, czyli typu zależności występującej pomiędzy zmienną objaśnianą a zmiennymi objaśniającymi.

W zależności od badanej sytuacji możliwe są trzy podejścia:

1. Oparte na ocenie wzrokowej rozrzutu punktów empirycznych (Xi, Yi), j = 1,2,…n na wykresie korelacyjnym.

2. Oparte na wykorzystaniu apriorycznej wiedzy o kształtowaniu się zależności między badanymi zjawiskami.

3. Heurystyczne, czyli oparte na metodzie prób i błędów.

Ocena jaką w modelu zastosowano odbywa się za pomocą analitycznych wskaźników odpowiadającym wynikom obserwacji zmiennej objaśniającej i zmiennych objaśnianych przedstawionych na płaszczyźnie w postaci układu współrzędnych. Wyniki obserwacji na zmiennej objaśniającej i zmiennych objaśnianych, które tworzą ciąg par liczbowych.

1 para obserwacji (X₁, Y₁)

2 para obserwacji (Y_x1, Y₂)

3 para obserwacji (X_n, Y_n)

Ciąg n par przedstawionych graficznie za pomocą punktów empirycznych na płaszczyźnie (ciąg n punktów na płaszczyźnie).

Wartości zmiennej objaśniającej przyjmujemy za odciętą a zmiennych objaśniających (y) przyjmujemy za rzędną.

Po naniesieniu punktów analizujemy rozrzut tych punktów na płaszczyźnie. Podejmujemy decyzję jaki jest typ zależności pomiędzy zmienną objaśniającą a zmienną objaśnianą.

Przykładowe rozrzuty punktów empirycznych (Xi, Yi) na płaszczyźnie w układzie współrzędnych i odpowiadające im typy zależności funkcyjnymi pomiędzy zmienną objaśniającą a zmienną objaśnianą.

Przebieg zmienności podstawowych funkcji stosowanych przy modelowaniu związków między zmienną objaśniającą (y) a zmienną objaśniającą (x).

Funkcja liniowa.

Równanie funkcji liniowej y = b₀ + b₁x, b₁ - ocena parametru b₁ odpowiadająca na pytanie jakie jest przeciętny przyrost wartości zmiennej objaśnianej (y) na jednostkę bezwzględną przyrostu wartości zmiennej objaśniającej (x).

y ∆ = b₀ + b₁ (x + 1)

y₁ = b₀ b₁x ₊ b₁ → ( b₀ + b₁x = y )

y ∆ = y + b₁

b₀ - jest to wartość zmiennej objaśnianej (y) przy założeniu, że x = 0 (przy zerowym poziomie wartości zmiennej objaśniającej). Przebieg zmienności funkcji linowej zależy od wartości parametru b₁ jeżeli b₁ > 0, to nachylenie prostej względem osi odciętych jest dodatnia. Gdy b₁ ≠ 0, to prosta równoległa y = b₁ do osi odciętych jest nachylona względem prostej b₁ < 0.

b₁ ∙ tg α

Funkcja potęgowa.

y = b₀ ∙ x^b1

b₀ > 0

Funkcja wykładnicza.

y = b₀ ∙ b₁^x

b₀ > 0

b₁ > 0

y = b₀ ∙ b₁^t

Obliczamy stopę wzrostu według wzory r = (b₁ - 1) ∙ 100%. Obliczona stopa wzrostu pokazuje jaki jest procentowy wzrost zmiennej objaśnianej (y) czyli badanego zjawiska w czasie, gdy wartość zmiennej objaśniającej (t) rośnie o jeden, czyli w szczególnym przypadku o jedną jednostkę czasową.

Funkcja wielomianowa stopnia drugiego.

y = b₀ + b₁x + b₂x²

1. b₁ < 0 ; b₂ > 0 parabola jest skierowana ramionami do góry i ma tylko jedno minimum.

2. b₁ > 0 ; b₂ < 0 parabola jest skierowana ramionami do dołu i ma tylko jedno maksimum.

y = b₀ + b₁x + b₂x²

y ` = b₁ + 2b₂x = 0

2b₂x = - b₁ → Xopt = -

yopt = b₀ + b₁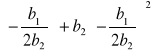

yopt = b₀ -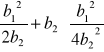

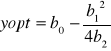
(max albo min)

Funkcja logistyczna.

b₀ > 0

b₂ > 1

b₂ > 0

Asymptota - prosta o równaniu y = b₀, która oznacza poziom nasycenia badanego wzrostu w czasie zjawiska.

Wykres funkcji logistycznej wychodzi z punktu o współrzędnych (0 ;
), b₁ > 1 , gwarantuje, że krzywa logistyczna ma punkt przegięcia.

Istota metody najmniejszych kwadratów.

Polega na oszacowaniu parametrów strukturalnych modelu postaci yi = β₀ + βα xi = β₀ + β₁ xi + e gdzie yi , β₀ , β₁ parametry strukturalne modelu, xi - wartość empiryczna zmiennej objaśniającej, ei - nieznane wartości składnika losowego, w taki sposób aby suma kwadratów odchyleń wartości empirycznych zmiennej objaśnianej od jej wartości teoretycznych wyznaczonych na podstawie równania modelu była minimalna.

SSE (b) =

SSE (b) - suma kwadratów reszt (dla błędu)

yi - wartości empiryczne zmiennej objaśnianej

- wartość teoretyczne zmiennej objaśnianej

Szacowanie parametrów strukturalnych modelu liniowego z jedną zmienną objaśnianą.

yi = β₀ + βα xi + ei

Zastosowanie MNK polegać będzie na rozwiązaniu zagadnienia optymalizacyjnego o postaci:

SSE (b₀, b₁) = Σ (yi
Σ (yi - b₀ - b₁xi) ² = min

Pochodna względem b₀ :

2 ∙ Σ (yi - b₀ - b₁xi) (- 1) = 0

Pochodna względem b₁ :

2 ∙ Σ (yi - b₀ - b₁xi) (- xi) = 0

Obliczamy pochodną cząstkową względem b₀ (xi yi) czyli zaobserwowanych wartości zmiennej objaśnianej i zmiennych objaśniających.

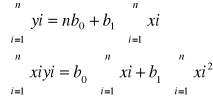
Jest to układ równań normalnych.

b₁ =

b₀ =

SSx = Σ (xi -
= Σ xi ² -
(Σ xi) ²

SSxy = Σ (xi -
) (yi -
) = Σ xiyi -
( Σxi) (Σyi)

W tym układzie sumy są wielkościami stałymi. Współczynniki występują przy niewiadomych b₀ i b₁.

Rozwiązaniem tego układu są wartości ocen parametrów strukturalnych b₀ i b₁.

Ilustracja graficzna metody najmniejszych kwadratów.

Warunki stosowalności metody najmniejszych kwadratów:

1) Warunek pierwszy wymaga, aby szacowane równanie modelu ekonometrycznego było liniowe względem zmiennych objaśniających, parametrów strukturalnych oraz składnika losowego, czyli postać takiego równania jest następująca:

yi = β₀ + β₁ xi₁ + β₂ xi₂ + … + β_k xi_k + e₁

2) Warunek drugi głosi, że liczba zaobserwowanych wartości zmiennych występujących w modelu n musi być większa od liczby szacowanych parametrów strukturalnych (k + 1).

n > k + 1

3) Trzeci warunek głosi, że kolumny macierzy X (k + 1 - kolumn) muszą być liniowo niezależne. Oznacza to, że każda zmienna objaśniająca powinna wnosić do modelu nową informację, odmienną od funkcji wnoszonych przez pozostałe zmienne objaśniające.

Wówczas r (X^T X) = k + 1 oraz det (X^T X) = 0

Własności modelu liniowego oszacowanego metodą najmniejszych kwadratów.

1) Suma wartości teoretycznych zmiennej objaśnianej
( i = 1,2,…,n) jest równa sumie wartości empirycznych tej zmiennej (yi) co zapisujemy następująco:

2) Suma reszt
jest równa zero.

natomiast suma kwadratów reszt:

3) Reszty
są nieskorelowane z wartościami poszczególnych zmiennych objaśniających, czyli nieskorelowane z wartościami xij (i = 1,2,…,n) (j = 0,1,2,…,k) .

(j = 0,1,2,…,k)

4) Reszty
są nieskorelowane z wartościami zmiennej objaśniającej.

Etap 5.

Weryfikacja modelu ekonometrycznego.

Wyróżniamy dwa podstawowe rodzaje weryfikacji modelu:

- weryfikacje merytoryczną

- weryfikację statystyczną

Weryfikacja merytoryczna polega na sprawdzeniu sensowności znaków ocen parametrów strukturalnych modelu. Przykład weryfikacji merytorycznej modelu:

Zweryfikować merytorycznie model ekonometryczny opisujący kształtowanie się konsumpcji w zależności od dochodów osobistych w Polsce w latach 1960 - 1990 na podstawie danych rocznych dla gospodarki polskiej.

2086,9 + 0,723 doch

konsump - oznacza wydatki na dobra materialne z dochodów osobistych w mld zł wyrażone w cenach stałych z 1990 roku.

doch - realne dochody osobiste ludności w mln zł wyrażone w cenach stałych z 1990 roku.

Weryfikacja statystyczna polega na sprawdzeniu czy model z dostateczną dokładnością odzwierciedla badany fragment rzeczywistości gospodarczej, czyli czy model jest dostatecznie dobrze dopasowany do danych empirycznych. Przeprowadza się ją przy wykorzystaniu dwóch podstawowych analiz:

- analizy wariancji zmiennej objaśnianej

- analizy ocen parametrów struktury stochastycznej modelu

W tych analizach wykorzystuje się następujące mierniki:

1) Odchylenie standardowe składnika losowego Se

2) Współczynnik zmienności składnika losowego (współczynnik wyrazistości) Ve

3) Błędy średnie szacunku ocen parametrów strukturalnych modelu D(b₁) = 0,1,2,..,k

4) Współczynnik determinacji R² i współczynnik zbieżności (jest odwrotnością współczynnika determinacji)

5) Wartość empiryczne statystyki T- Studenta, które oblicza się w stosunku do poszczególnych ocen parametrów strukturalnych - służą do badania statystycznej istotności ocen parametrów strukturalnych modelu (t_j emp = 0,1,2,…k )

6) Wartość empiryczna statystyki F - Snedecora-Fishera, którą stosuje się w odniesieniu do całego modelu i służy do sprawdzenia hipotezy statystycznej, czy zachodzi istotna statystycznie zależność między zmienną objaśnianą a którąkolwiek ze zmiennych objaśniających.

1) Odchylenie standardowe składnika losowego.

Przeciętna różnica pomiędzy wartościami empirycznymi (rzeczywistymi) zmiennej objaśnianej a jej wartościami teoretycznymi obliczonymi na podstawie oszacowanego modelu liniowego
.

2) Współczynnik zmienności składnika losowego określa, jaką część średniej wartości zmiennej objaśnianej stanowi jej odchylenie standardowe. W praktyce im mniejsza jest ta wartość tym model jest lepiej dopasowany do danych empirycznych

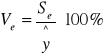
3) Współczynnik determinacji określa on jaka część całkowitej zmienności zmiennej objaśnianej została wyjaśniona przez model, jest więc miarą stopnia, w jakim model wyjaśnia kształtowanie się zmiennej objaśnianej. Współczynnik ten wyrażany jest zazwyczaj w procentach.

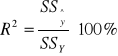
Przedziały wartości R² dla oceny jakości modelu:

a) jeżeli R² ≥ 80 % to mówimy, że model w bardzo wysokim stopniu wyjaśnił kształtowanie się zmiennej objaśnianej

b) jeżeli 60% ≤ R² < 80 % to mówimy, że model w stopniu zadowalającym wyjaśnił kształtowanie się zmiennej objaśnianej

c) jeżeli 50% ≤ R² < 60 % to mówimy, że model w stopniu dostatecznym wyjaśnił kształtowanie się zmiennej objaśnianej

d) ) jeżeli R² < 50 % model jest słabej jakości i nie wyjaśnia w stopniu dostatecznym kształtowanie się zmiennej objaśnianej

4) Błędy średnie szacunku parametrów strukturalnych modelu.

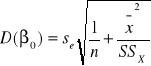
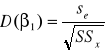
Wyznaczone błędy informują nas o rzędzie dokładności oszacowania parametrów strukturalnych. W ekonometrii przyjmuje się, że błąd nie powinien przekraczać 50% wartości szacowanego parametru. Jeżeli przekroczy 50% to zmienną objaśniającą, która występuje przy takiej ocenie obciążonej dużym błędem należy usunąć z równania modelu i model należy oszacować ponownie bez tej zmiennej.

5) Wartość empiryczne statystyki T- Studenta, które oblicza się w stosunku do poszczególnych ocen parametrów strukturalnych służą do badania statystycznej istotności poszczególnych ocen parametrów strukturalnych modelu.

Zastosowanie testu t - Studenta do badania statystycznej istotności poszczególnych parametrów strukturalnych modelu.

H₀ - parametr występujący przy j - tej zmiennej objaśniającej jest statystycznie nieistotnie różni się od zera.

H₁ - parametr występujący przy - tej zmiennej objaśniającej statystycznie istotnie różni się od zera.

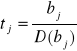
| tj | > t α; n - k - 1

tj < - t α; n - k - 1 tj < 0

tj > t α; n - k - 1 tj > 0

Jeżeli to oznacza, że wartość empiryczna statystyki t - Studenta znalazła się w obszarze krytycznym i istnieje podstawa do odrzucenia hipotezy zerowej na korzyść alternatywnej. Zatem ocena β_j istotnie różni się od zera a to oznacza, że zmienna objaśniająca przy, której występuje ta ocena ma istotny wpływ na kształtowanie się zmiennej objaśnianej.

| tj | < t α; n - k - 1

tj > - t α; n - k - 1 tj < 0

tj < t α; n - k - 1 tj > 0

Jeżeli to nie ma podstaw do odrzucenia hipotezy zerowej tzn. że β_j nie różni się istotnie od zera. Zatem zmienna występująca przy takiej ocenie nie ma istotnego wpływu na kształtowanie się zmiennej objaśnianej. Jeżeli okaże, się że kilka parametrów nieistotnie różni się od zera, należy uznać odpowiadające im zmienne za statystycznie nieistotne. Dlatego też należy te zmienne wyeliminować ze zbioru zmiennych objaśniających i model oszacować ponownie. Następnie należy poddać go weryfikacji dla mniejszej liczby zmiennych objaśniających.

Estymacja parametrów strukturalnych modeli nieliniowych.

1. Podstawowe typy modeli nieliniowych.

Modele liniowe względem parametrów, ale nieliniowe względem zmiennych objaśniających są sprowadzane do liniowych poprzez wprowadzenie dodatkowych zmiennych objaśniających; można stosować MNK.

2. Modele nieliniowe zarówno względem parametrów strukturalnych jak i względem zmiennych objaśniających sprowadzane są do modeli liniowych za pomocą tzw. transformacji liniowej zmiennych występujących w modelu (zmiennej objaśnianej i zmiennych objaśniających; można stosować MNK (potęgowe i wykładnicze)

3. Modele nieliniowe, które nie dają się transformować do modeli liniowych względem parametrów i zmiennych są to tzw. modele istotnie nieliniowe. Do szacowania ich parametrów strukturalnych można stosować metodę literacyjną np. Gausa Newtona, metodę największej wiarygodności.

Przykłady modeli poszczególnych typów modeli nieliniowych.

Typ I Model wielomianowy stopnia drugiego.

Typ II Modele potęgowe i wykładnicze

Model wykładniczy

Model potęgowy

Typ III Model CES - funkcja produkcji o stałej elastyczności substytucji nakładów czynników produkcji.

Q - zmienna wielkości produkcji w ujęciu wartościowym

pk ^{- α} - nakłady kapitału

β - nakłady siły roboczej

Estymacja parametrów strukturalnych modeli nieliniowych typu III:

I etap - linearyzacja modelu liniowego

II etap - wyznaczenie ocen parametrów strukturalnych liniowego modelu pomocniczego - przekształcony model

Model wykładniczy (nieliniowy) - oryginalny

III etap wyznaczenie wartości ocen parametrów strukturalnych modelu oryginalnego

IV etap - weryfikacja statystyczna modelu pomocniczego i oryginalnego. Zasada: jeżeli model pomocniczy dobrze dopasowany do danych empirycznych to możemy zakładać, że model oryginalny jest dobrej jakości.

Postępowanie linearyzacyjne.

a) Model potęgowy.

Krok 1 - linearyzacja modelu potęgowego. Możemy oba logarytmy zastosować.

Wprowadzenie zmiennych i parametrów pomocniczych.

Stąd:

model pomocniczy liniowy

Krok 2 - szacowanie parametrów strukturalnych modelu pomocniczego (β₀^*, β₁, β₂, … , β_k ) metodą MNK na podstawie danych przekształconych.

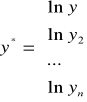
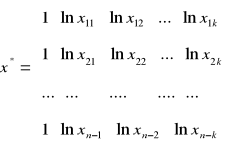
n - liczba badanych okresów

Na podstawie danych przekształconych wyznaczenie ocen parametrów strukturalnych modelu pomocniczego b₀^*, b₁, b₂, … , b_k

Krok 3 - obliczanie ocen parametrów strukturalnych modelu oryginalnego:

, natomiast oceny b₁, b₂, … , b_k w modelu oryginalnym są takie same jak w modelu pomocniczym.

b) Model wykładniczy.

Krok 1 - linearyzacja modelu wykładniczego

Nie przekształcamy wartości zmiennych objaśniających stąd:

Krok 2 - szacowanie parametrów strukturalnych modelu pomocniczego (β₀^*, β₁^*, β₂^*, … , β_k^* ), MNK na podstawie danych przekształconych

Na podstawie danych przekształconych wyznaczanie ocen parametrów strukturalnych modelu pomocniczego b₀^*, b₁^*, b₂^*, … , b_k^*

Krok 3 - obliczanie ocen parametrów strukturalnych modelu oryginalnego

c) Model logistyczny.

Krok 1 - linearyzacja

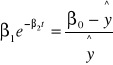
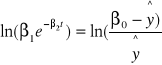
Wprowadzenie zmian i parametrów pomocniczych:

stąd:

Natomiast b₀ wyznacza się ze wzoru:

y₁ - oznacza wartość zmiennej objaśnianej w okresie początkowym t₁

y_n - oznacza wartość zmiennej objaśnianej w okresie końcowy t_n

y_s - oznacza wartość zmiennej objaśnianej w okresie środkowym t_s , przy czym t_s wyznaczamy ze wzoru:

t_s = (t₁ + t_n) / 2

- jeżeli t_s , jest wielkością całkowitą to wartość y₀ odczytujemy bezpośrednio z badanego szeregu czasowego

- jeżeli t_s , jest liczbą niecałkowitą, wtedy poszukiwaną wartość t_s znajdujemy według interpolacji liniowej za pomocą następującego wzoru:

Przy:

t_s-1 < t_s < t_s+1

Krok 2 - oszacowanie parametrów strukturalnych modelu pomocniczego na podstawie danych.

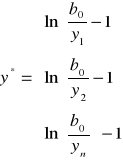
Ocena parametru β₁^* i β₂^* :

b₁^* i b₂^* - uzyskujemy oceny parametrów strukturalnych modelu pomocniczego

b₀ - ocena oryginalna wyznaczona poza modelem

Krok 3 - obliczenie ocen parametrów strukturalnych modelu oryginalnego.

b₁ = e^b1* i b₂ (b₀ to ocena oryginalna).

Konstrukcja modelu optymalizacyjnego.

Modele optymalizacyjne służą do planowania działalności gospodarczej przy wykorzystaniu modeli optymalizacyjnych. Planowanie to ustalanie celów gospodarczych i znajdowanie najlepszych rozwiązań ekonomicznych prowadzących do ich osiągnięcia. Modele optymalizacyjne prowadzą do opracowania optymalnych planów produkcji.

Plan - program działania, dyrektywa.

Model optymalizacyjny - jest układem logicznie powiązanych zależności w postaci równań lub nierówności, Mogą być liniowe i nieliniowe opisujące warunki i sposób funkcjonowania badanej jednostki gospodarczej, w której mogą być jednostki w skali mikro, mezo i makroekonomicznej.

Model optymalizacyjny liniowy o postaci standardowej - zapis ogólny:

FC: c^Tx = max

WC: Ax ≤ b

WB: x ≥ 0

Model optymalizacyjny składa się z trzech części:

- FC - funkcji celu

- WO - warunków ograniczających

- WB - warunków brzegowych

Funkcja celu (FC) jest to równanie stanowiące miernik stopnia osiągnięcia celu, do którego zmierza decydent.

Warunki ograniczające (WO) - odzwierciedlają za pomocą równań i nierówności liniowych warunki i sposób funkcjonowania badanego układu gospodarczego.

WO :

- nie przekraczanie limitów

- opracowanie związane z pracą i kapitałem, ich zasoby, surowce itp.

- sposób funkcjonowania jednostki gospodarczej - są to stosowane w procesie produkcji techniki, technologie wytwórcze

- ograniczenie możliwości zbytu wytwórczej produkcji

Warunki brzegowe (WB) - wyrażają żądanie, aby występujące w modelu zmienne decyzyjne przedstawione w postaci wektora x, reprezentujące działalności produkcyjne przyjmowały wyłącznie wartości nieujemne.

Elementy, z których zbudowany jest model optymalizacyjny (dwie grupy elementów):

- zmienne decyzyjne

- parametry

W modelu występują wielkości zmienne, które zwane są parametrami i wielkości, które należy ustalić, zwane zmiennymi decyzyjnymi.

Zmienne decyzyjne określają, w modelu działalności produkcyjne brane pod uwagę przy organizowaniu produkcji, w modelu są niewiadomymi. W wyniku rozwiązania modelu uzyskujemy ich wartości liczbowe, które tworzą optymalny plan produkcji.

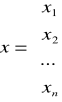
Plan produkcji może być:

- optymalny

- dopuszczalny

- niedopuszczalny

Optymalny plan produkcyjny to plan, zbiór wartości liczbowych, zmiennych decyzyjnych, który spełnia jednocześnie wszystkie WO, WB i funkcja celu osiąga wartość maksymalna lub minimalną.

Dopuszczalny plan produkcyjny to zbiór wartości, zmiennych decyzyjnych, który spełnia tylko WO i WB. Funkcja celu nie osiąga wartości optymalnej.

Niedopuszczalny plan produkcyjny - plan, taki układ zmiennych decyzyjnych, które nie spełniają choćby jednego WO lub jednego WB.

W modelu występują trzy rodzaje parametrów:

- parametry funkcji celu

- parametry techniczno - ekonomiczne

- wyrazy wolne

Planujemy n działalności gospodarczej.

Parametry funkcji celu wyrażają jednostkowe wartości przyjętego kryterium celu w odniesieniu do poszczególnych działalności produkcyjnych uwzględnionych w modelu.

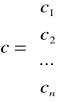
max - oznacza maksymalną wartość funkcji celu.

Parametry techniczno - ekonomiczne w modelu optymalizacyjnym wyrażają zużycie środków limitowanych - zasobów na jednostkę działalności produkcyjnej lub zużycie jednostek pewnej działalności produkcyjnej na jednostkę innej działalności produkcyjnej.

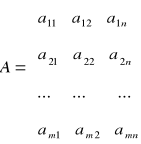
warunki ograniczające

Zmienne decyzyjne:

m - liczba warunków ograniczających występujących w modelu.

n - liczba zmiennych decyzyjnych występujących w modelu.

Wielkości występujące po prawej stronie warunków ograniczających wyrażają m.in. wielkości zasobów i środków limitowanych znajdujących się w dyspozycji jednostki gospodarczej.

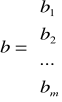
Wektor składający się z zer:

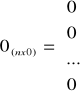
Główne cechy charakterystyczne modeli ekonometrycznych optymalizacyjnych - porównanie struktury obydwu klas modeli.

Modele ekonometryczne	Modele optymalizacyjne
1. Przeznaczenie
- służy do opisu zależności między zjawiskami gospodarczymi - czyli do diagnozowania stanu istniejącego w badanym fragmencie rzeczywistości działalności gospodarczej, - wykorzystuje się do prognozowania zjawisk gospodarczych, czyli przewidywania przyszłego ich stanu oraz symulacji zachowań obiektów gospodarczych.	- służą do planowania działalności gospodarczej oraz symulacji zachowań obiektów gospodarczych.
2. Parametry modelu
- parametry strukturalne i parametry struktury stochastycznej są wielkościami nieznanymi	- parametry funkcji celu, techniczno - ekonomiczne, wyrazy wolne są wielkościami znanymi, nie są celem poszukiwań

3. Zmienne
- zmienna objaśniana i zmienne objaśniające, ich wartości są dane	- zmienne decyzyjne, ich wartości są niewiadomymi w modelu. W wyniku rozwiązywania modelu uzyskuje się zbiór wartości liczbowych zmiennych decyzyjnych, który tworzy optymalny plan produkcji
4. Konstrukcja w sensie matematycznym
- równanie lub układ równań (liniowe lub nieliniowe), na przykład: model liniowy y = β0 + β1 x1 +…+ βk xβk + e model potęgowy y = β0 + β1^β1∙…∙ xk^βe ∙ e model wykładniczy y = β0 ∙ β1^x1∙…∙ βk^xk∙ e	- układ równań i nierówności liniowych bądź nieliniowych: C^T x = max Ax ≤ b x ≥ 0

Optymalizacja decyzji gospodarczych, czyli poszukiwanie optymalnych planów produkcji.

Przykład 5.

Przedsiębiorstwo produkuje dwa wyroby W₁ i W₂. Wiadomo, że w procesie produkcji tych wyrobów zużywa się wiele środków produkcji, spośród których tylko dwa (A i B) są limitowane w tym przedsiębiorstwie. Znane są te limity, które wynoszą odpowiednio A - 96000 jednostek, B - 80000 jednostek. Znane są również nakłady środków limitowanych na wyprodukowanie jednostki wyrobów W₁ i W₂ , które kształtują się następująco:

Środki limitowane	Wyroby		Limit środków produkcji
		W1		W2
A	16	24	96000
B	16	10	80000

Ponadto wiadomo, że zdolności produkcyjne jednego z wydziałów przedsiębiorstwa są takie, że nie pozwalają wyprodukować więcej niż 3000 sztuk wyrobu W₁ i 4000 sztuk wyrobu W₂. Działająca w przedsiębiorstwie komórka marketingowa ustaliła właściwe proporcje produkcji, które kształtują się jak 3 / 2 (na 3 jednostki wyrobu W₁ powinny przypadać 2 jednostki wyrobu W₂). Ceny sprzedaży jednostki wyrobu wynoszą W₁ = 30 zł, W₂ = 40 zł.

Na tej podstawie należy ustalić optymalne rozmiary produkcji wyrobów W₁ i W₂ w sztukach fizycznych przy założeniu, że uzyskany przychód ze sprzedaży będzie maksymalny.

Warunki ograniczające:

1. Bilans zużycia środka produkcji A:

16 x₁ + 24 x₂ ≤ 96000 jednostki środka produkcji A

2. Bilans zużycia środka produkcji B:

16 x₁ + 20 x₂ ≤ 80000 jednostki środka produkcji B

3. Proporcje między wielkością produkcji wyrobu W₁ i W₂ :

(sztuk), proporcje produkcji: na 3 jednostki wyrobu W₁ , powinny przypadać 2 jednostki wyrobu W₂.

4. x₁ ≤ 3000 (sztuki fizyczne)

5. x₂ ≤ 4000 (sztuki fizyczne)

Funkcja celu: 30 x₁ + 40 x₂ = max

Warunki ograniczające:

16 x₁ + 24 x₂ ≤ 96000

16 x₁ + 10 x₂ ≤ 80000

x₁ ≤ 3000

x₂ ≤ 4000

Warunki brzegowe: x₁ ≥ 0, x₂ ≥ 0

---