UNIWERSYTET TECHNOLOGICZNO - PRZYRODNICZY W BYDGOSZCZY

WYDZIAŁ BUDOWNICTWA I INŻYNIERII ŚRODOWISKA

Ćwiczenie projektowe z przedmiotu

TEORIA SPRĘŻYSTOŚCI I PLASTYCZNOŚCI

„Stateczność pręta prostego.”

Stateczność - właściwość układu do powracania do warunków równowagi statycznej, w przypadku gdy został z tych warunków wytrącony.

Jeśli układ po wytrąceniu z warunków równowagi statycznej w dalszym ciągu się od nich oddala - nazywany jest niestatecznym.

Utrata statecznosci konstrukcji jest zagadnieniem niezwykle ważnym i skomplikowanym.

Zajmę sie teraz podaniem analitycznych warunków zapewnienia równowagi statecznej dla bardzo prostej konstrukcji, jaka jest osiowo sciskany pret pryzmatyczny, wykonany z materiału o własnosciach fizycznych okreslonych prawem Hooke'a.

Zacznę najepierw jednak od prostego „ideowego” objaśnienia trzech postaci równowagi w jakich konstrukcja może sie znajdować.

Jeżeli po dowolnie małym wychyleniu z pierwotnego położenia równowagi ruch ciała jest taki, że wychylenia jego punktów nie są większe od tych początkowych to taką równowagę nazywamy stateczną (trwała).

W przeciwnym przypadku równowaga jest niestateczna (nietrwała, chwiejna).

Można jeszcze wyróżnić szczególne położenie równowagi zwane równowagą obojetną w której punkty ciała pozostają w położeniu po wychyleniu. Opisaną sytuację można zobrazować traktując konstrukcję jako ciężka kulkę w różnych warunkach podparcia znajdująca sie w potencjalnym polu sił.

Równowadze statecznej I odpowiada minimum energii potencjalnej układu, a w równowadze chwiejnej III maksimum. W stanie równowagi obojętnej II wartość energii potencjalnej przy dowolnie małym wychyleniu pozostaje stała.

Z utratą stateczności mamy do czynienia, gdy niewielka zmiana przyczyny powoduje bardzo dużą zmianę skutku. Idealnie sprężysty pręt przy pewnej wartości siły ściskającej zmienia w sposób nagły swą prostoliniową postać i przyjmuje położenie wygięte. W środku rozpiętości pręta będzie występował moment jako skutek działania siły ściskającej na pewnym mimośrodzie, na ramieniu równym wartości ugięcia tego pręta w.

W teorii I-go rzędu rozpatrujemy konstrukcje w stanie nieodkształconym (stosujemy zasadę zesztywnienia). Jeżeli siły osiowe są znaczne a pręt wiotki należy odrzucić zasadę zesztywnienia i uwzględnić wpływ sił osiowych na powstawanie momentów. Stosujemy teorię II-go rzędu.

Rozważmy, ściskany osiowo siłą P pręt przegubowo podparty na obu końcach, wykonany z materiału liniowo sprężystego o module Younga E i nadajmy mu jakimś impulsem poprzecznym dowolnie małe początkowe ugięcie w płaszczyźnie najmniejszej sztywności zginania. Jeżeli po usunięciu przyczyny ugięcia powróci on do swej początkowej prostoliniowej postaci, oznacza to, że znajduje sie w równowadze statecznej.

Powtarzając rozumowanie wraz ze zwiększaniem wartości siły P dojdziemy do sytuacji, w której pręt po usunięciu przyczyny początkowego ugięcia pozostanie krzywoliniowy (nie powróci do swej pierwotnej prostoliniowej formy). Oznacza to, że tymrazem pręt znajduje się w stanie równowagi obojętnej, a siłę, przy której to nastąpiło nazywać będziemy siła krytyczna P_kr. Tak wiec:

SIŁA KRYTYCZNA - to siła, przy której osiowo ściskany pręt znajduje się w stanie równowagi obojętnej.

Gdy siła osiągnie wartość krytyczną P_kr pręt traci stateczność (ulega wyboczeniu), a jego ugięcia mogą być dowolnie duże. Wyboczenie jest to zatem utrata przez ściskany pręt stanu równowagi statecznej na rzecz równowagi obojętnej lub niestatecznej.

Wyboczenie może mieć jedną z trzech postaci:

• Giętną - pręt ulega wygięciu w płaszczyźnie najmniejszej jego sztywności

• Skrętną - pręt skręca się wokół osi podłużnej

• Giętno - skrętną - następuje wygięcie pręta z równoczesnym jego skręceniem

Niestateczność ogólna elementów zginanych to zwichrzenie. Występuje, gdy moment zginający osiągnie wartość krytyczną (M_cr). Jest inicjowane wyboczeniem pasa ściskanego z płaszczyzny zginania i natychmiast przechodzi w skręcanie (jest zbliżone do wyboczenia giętno-skrętnego).

Możliwość utraty stateczności pręta zależy od jego smukłości. W miarę wzrostu długości wyboczeniowej pręta l_w, rośnie jego wrażliwość na utratę stateczności ogólnej.

Długość wyboczeniowa związana jest ze współczynnikiem wyboczeniowym α.

l_w = α · l

Wartości współczynnika długości wyboczeniowej α zależnego od warunków podparcia podano na rysunku poniżej:

Naprężenia krytyczne

Zakres ważności wzoru Eulera na siłę krytyczną jest ograniczony własnościami fizycznymi materiału ściskanego pręta. Ponieważ materiał analizowanego pręta był z założenia materiałem liniowo sprężystym to naprężenia normalne w pręcie nie mogą przekraczać R_H - granicy stosowalności prawa Hooke`a (granicy proporcjonalności)

Wyniki analiz prętów pozwalają napisać jednolity wzór na siłę krytyczną, nazywaną siłą krytyczną Eulera w postaci:

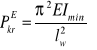
W celu wyznaczenia zakresu stosowalności wzoru Eulera dokonamy jego przekształcenia. Wpierw podzielimy obustronnie przez pole przekroju poprzecznego A:

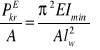
Następnie definiujemy pojęcie naprężenia krytycznego:

Smukłość λ jest liczbą charakteryzującą pręt. Zależy ona od właściwości przekroju, długości wyboczeniowej pręta (więc od warunków podparcia) i od własności materiału pręta. Smukłość pręta definiujemy w nastęujący sposób:

Gdzie: minimalnym promieniem bezwładności przekroju poprzecznego:

Znając E dla materiału pręta oraz dopuszczalne naprężenie możemy wyznaczyć jego (dopuszczalną) właściwą smukłość.

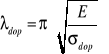
Możemy otrzymać zależność:

Powyższy zapis oznacza naprężenie krytyczne Eulera

Na wykresie zależności σ_kr od λ, wykresem funkcji
jest hiperbola, której zakres ważności jest ograniczony od góry, na osi rzędnych, wartością R_H.

Podsumowując:

Tak długo, jak P < Pkr pręt zachowuje się w sposób „stateczny”, tzn. znajduje się w stanie

początkowej równowagi prostoliniowej. Wówczas, gdy siła osiągnie wartość krytyczną P_kr pręt traci stateczność (ulega wyboczeniu), a jego ugięcia mogą być dowolnie duże.

Wyboczenie jest to zatem utrata przez ściskany pręt stanu równowagi statecznej na rzecz równowagi obojętnej lub niestatecznej.

---