SPEKTROSKOPIA ELEKTRONOWEGO REZONANSU PARAMAGNETYCZNEGO

Materiały magnetyczne.

Diamagnetyzm.

Podstawową wielkością, która charakteryzować nam będzie własności magnetyczne substancji jest podatność magnetyczna określona wzorem:

, (1)

gdzie: M jest to namagnesowanie zdefiniowane jako moment magnetyczny przypadający na jednostkę objętości, H jest makroskopowym natężeniem pola magnetycznego. W układzie jednostek CGS Gaussa χ jest bezwymiarowe, jednakże często podatność magnetyczna bywa zdefiniowana w odniesieniu do jednostki masy lub mola substancji i wtedy wyrażamy ją w cm³/g lub w cm³/mol. Substancje o małej, ujemnej wartości podatności magnetycznej nazywamy diamagnetykami. Substancje o niewielkiej ale dodatniej podatności nazywamy paramagnetykami natomiast dla ferromagnetyków podatność jest dodatnia i duża lub bardzo duża.

Atomy lub cząsteczki substancji diamagnetycznych nie posiadają momentów magnetycznych. Natomiast jeśli umieścimy diamagnetyk w zewnętrznym polu magnetycznym, wówczas ładunki elektryczne dążą do częściowego ekranowania wnętrza ciała przed przyłożonym polem magnetycznym. Zatem stosownie do znanego z elektrodynamiki prawa Lenza, następuje indukowanie się prądu ekranującego, który z kolei indukuje moment magnetyczny o zwrocie przeciwnym do przyłożonego zewnętrznego pola magnetycznego. Moment magnetyczny związany z tym prądem nosi nazwę momentu diamagnetycznego. Efektem oddziaływania zewnętrznego pola magnetycznego z wyindukowanym momentem diamagnetycznym jest wypychanie próbki diamagnetycznej z pola magnetycznego.

Podatność diamagnetyczna obliczona przez Langevina wyraża się wzorem:

, (2)

gdzie: Z - liczba atomowa, e - ładunek elektronu, N - liczba atomów przypadająca na jednostkę objętości, m - masa elektronu, c- prędkość światła, r_śr - średnia odległość elektronu od jądra.

Typowe wartości wyznaczone doświadczalnie dla gazów szlachetnych przedstawiono w tabeli 1.

Tabela 1

	He	Ne	Ar	Kr	Xe
χM 10^-6 cm^3/mol	-1.9	-7.2	-19.4	-28	-43

W przypadku wielu układów cząsteczkowych cząsteczek podatność diamagnetyczna zawiera dodatkowy człon, który związany jest z tzw. paramagnetyzmem van Vlecka. Układ taki może być zarówno dia- jak para- magnetykiem, w zależności od tego, który człon jest większy.

Idealny diamagnetyzm zaobserwowano w nadprzewodnikach. Okazuje się, że poniżej temperatury przejścia w stan nadprzewodzący w nadprzewodniku obserwujemy tzw. efekt Meissnera, który polega na wyindukowaniu tak silnego momentu diamagnetycznego, który redukuje pole magnetyczne w nadprzewodniku do zera.

Paramagnetyzm.

Paramagnetyzm związany jest z momentami magnetycznymi elektronów w atomach i cząsteczkach. Na ogół w na skutek wzbudzeń termicznych całkowite namagnesowanie paramagnetyków jest równe zero. Dopiero umieszczenie paramagnetyka w zewnętrznym polu magnetycznym powoduje porządkowanie jego momentów magnetycznych.

Paramagnetyzm można zaobserwować w następujących układach:

1. w atomach, cząsteczkach i defektach sieciowych, mających nieparzystą liczbę elektronów. Przykłady: swobodne atomy sodu, gazowy tlenek azotu (NO), wolne rodniki organiczne, jak np. trójfenylometyl (C(C₆H₅)₃), centra fluoru w halogenkach alkalicznych,

2. w swobodnych atomach i jonach z częściowo wypełnioną powłoką wewnętrzną: pierwiastki grupy przejściowej, pierwiastki ziem rzadkich i aktynowce. Przykłady: Mn²⁺, Gd³⁺, U⁴⁺. Wiele z tych jonów wykazuje własności paramagnetyczne nawet po wbudowaniu w ciało stałe, jakkolwiek nie zawsze,

3. w kilku związkach o parzystej liczbie elektronów, jak np. cząsteczkowy tlen i podwójne rodniki organiczne,

4. w metalach.

Podatność paramagnetyków otrzymana przez Langevina wyraża się wzorem:

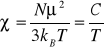
, (3)

gdzie: N - ilość atomów na jednostkę objętości, μ - moment magnetyczny pojedynczego atomu,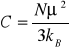
- stała Curie. Wzór (2) nosi nazwę prawa Curie.

Ferromagnetyzm.

Ferromagnetyk to substancja posiadająca spontaniczny, występujący nawet w nieobecności zewnętrznego pola magnetycznego, moment magnetyczny. Istnienie spontanicznego momentu magnetycznego wskazuje na to, że spiny i momenty magnetyczne elektronów ustawione są w pewien regularny sposób. Zakłada się, że za porządek ferromagnetyczny odpowiedzialne jest pole wymiany (pole Weissa). Pole wymiany traktowane jest jak pole magnetyczne o indukcji B_E, która może osiągać wartości rzędu
. W przybliżeniu średniego pola zakłada się, że na każdy atom o niezerowym momencie magnetycznym oddziałuje pole o indukcji proporcjonalnej do namagnesowania M.

(4)

gdzie λ oznacza stałą niezależną od temperatury. Zgodnie z powyższym wzorem każdy spin „widzi ” średnie namagnesowanie pochodzące od wszystkich pozostałych spinów. W rzeczywistości może on „widzieć” tylko swoich najbliższych sąsiadów, jednak przyjęte uproszczenie jest wystarczające do opisu zagadnienia w pierwszym przybliżeniu.

Porządkującemu oddziaływaniu pola wymiany przeciwstawiają się drgania termiczne - powyżej temperatury Curie T_C uporządkowanie spinów zostaje zniszczone, czego skutkiem jest zanikanie spontanicznego namagnesowania. Temperatura Curie oddziela obszar występowania nieuporządkowanej fazy paramagnetycznej, w T > T_C, od obszaru występowania uporządkowanej fazy ferromagnetycznej w temperaturze T < T_C. Temperaturę Curie możemy wyrazić za pośrednictwem stałej λ. W fazie paramagnetycznej zewnętrzne pole magnetyczne pojawienie się pewnego skończonego namagnesowania, która z kolei powoduje pojawienie się skończonego pola wymiany B_E. Jeżeli ^χ_P oznacza podatność paramagnetyczną, to:

(5)

Namagnesowanie jest więc równe iloczynowi stałej podatności i natężenia pola tylko wtedy, gdy stopień uporządkowania układu jest mały, ma to miejsce, gdy dana substancja jest w stanie paramagnetycznym.

Podatność paramagnetyczną określa prawo Curie:

(6)

gdzie C oznacza stałą Curie. Wykorzystując poprzednie zależności można zapisać związek (z którego wynika prawo Curie-Weissa):

(7)

Równanie (4) posiada osobliwość w T=T_C=Cλ (T_C- temperatura Curie). W tej temperaturze (i poniżej) występuje spontaniczne namagnesowanie próbki, ponieważ gdy χ jest nieskończone M może osiągnąć skończoną wartość dla B_a=0.

Domeny magnetyczne.

W temperaturach znacznie niższych od temperatury Curie momenty magnetyczne w skali mikroskopowej są równoległe do siebie. Jednakże, rozpatrując próbkę jako całość stwierdzamy, ze jej wypadkowe namagnesowanie jest dużo mniejsze od namagnesowania wynikającego z istnienia pola Weissa.

Próbki składają się z małych obszarów zwanych domenami. W każdej domenie lokalne namagnesowanie odpowiada stanowi nasycenia. Jednak kierunki namagnesowania różnych domen nie są równoległe do siebie.

Wzrost wypadkowego namagnesowania ferromagnetyka pod wpływem zewnętrznego pola magnetycznego jest związany z dwoma niezależnymi procesami:

• w słabych zewnętrznych polach magnetycznych objętość domen, których namagnesowanie skierowane jest wzdłuż kierunku przyłożonego pola, zwiększa się kosztem objętości domen zorientowanych w innych kierunkach

• w silnych polach namagnesowanie domen obraca się w kierunku zewnętrznego pola

Bezpośrednim dowodem na istnienia struktury domenowej są fotografie granic domen otrzymane metodą obrazów proszkowych.

Ścianą Blocha w krysztale nazywamy warstwę przejściową, która rozdziela sąsiadujące ze sobą domeny namagnesowane w różnych kierunkach. Całkowita zmiana kierunku spinu między domenami nie ma charakteru nieciągłego skoku w obszarze jednej płaszczyzny atomowej, lecz następuje w sposób stopniowy na przestrzeni wielu płaszczyzn atomowych. Energia wymiany jest mniejsza, gdy zmiana kierunku spinu rozkłada się na wiele spinów.

Landau i Lifszyc wykazali, że występowanie struktury domenowej jest konsekwencją istnienia różnych wkładów do energii całkowitej ferromagnetyka: energii wymiany, energii anizotropii i energii magnetycznej.

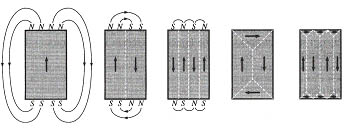
Rys.1.Schemat powstawania struktury domenowej w ferromagnetyku.

Przyczyną powstawanie struktury domenowej jest dążenie układu do osiągnięcia stanu o najniżej energii. Rysunek nr 1 obrazuje jak w wyniku powstawania domen w pewnym obszarze ferromagnetyka bieguny poszczególnych domen kompensują się nawzajem, co prowadzi do obniżenia energii układu. Dany obszar podzielony na dwie domeny posiada prawie o połowę mniejszą energię niż jego jednodomenowy odpowiednik, przy podziale na cztery domeny energia obniża się do ¼ stanu początkowego.

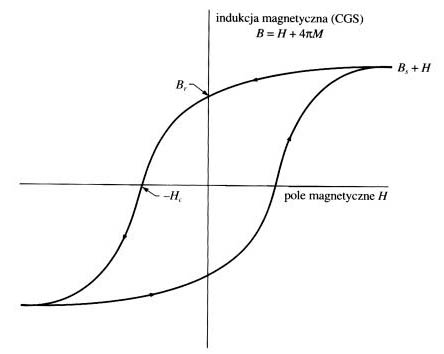
Rys.2.Pętla histerezy ferromagnetyka.

Pole koercji
- pole, jakie należy przyłożyć, aby zredukować indukcję B do zera (jest to najczulszy parametr charakteryzujący własności materiału ferromagnetycznego, który można kontrolować).

Indukcja pola remanencji
-odpowiada wartości B dla H=0. Dla dużych wartości pola
.

Anizotropia magneto-krystaliczna.

Za anizotropie magnetokrystaliczną kryształu ferromagnetycznego odpowiedzialna jest energia, która powoduje, że magnesuje się on łatwiej wzdłuż pewnych wyróżnionych kierunków krystalograficznych, nazywanych kierunkiem łatwego magnesowania. Energię tę nazywamy energią magnetokrystaliczną lub energią anizotropii. Jej pochodzenia nie można wyjaśnić rozpatrując tylko izotropowe oddziaływania wymiany.

Jednym ze źródeł anizotropii magnetokrystalicznej jest asymetria w przekrywaniu się rozkładów elektronów sąsiednich jonów (ze względu na oddziaływanie spin-orbita rozkład ma kształt elipsoidalny a nie kulisty). Asymetria jest związana z kierunkiem spinu, obrót spinu względem osi kryształu zmienia energię wymiany, a także zmienia energię oddziaływania elektrostatycznego pomiędzy rozkładami ładunku par atomów.

Żelazo krystalizuje w strukturze regularnej, a krawędzie sześciennej komórki elementarnej są kierunkami łatwego magnesowania (Rys.3).

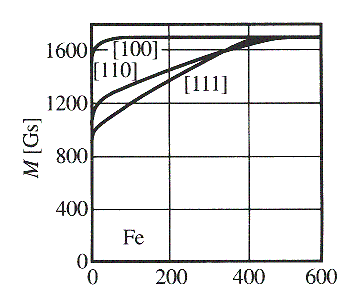
Rys.3.Wykres namagnesowania w funkcji zewnętrznego pola magnetycznego dla różnych kierunków krystalograficznych w monokrysztale Fe.

Wyrażenie na energię anizotropii:

(8)

gdzie:
-kosinusy kierunkowe pomiędzy kierunkiem namagnesowania a krawędziami sześcianu.

- stałe anizotropii

Dla żelaza w temperaturze pokojowej:

Klasyczny opis zjawiska elektronowego rezonansu paramagnetycznego (EPR). Precesja momentu paramagnetycznego w zewnętrznym polu magnetycznym.

W zewnętrznym stałym polu magnetycznym
na moment magnetyczny

(9)

-moment pędu, γ-czynnik żyromagnetyczny

który nie jest do niego równoległy działa skręcający moment siły.

(10)

Pod jego działaniem moment magnetyczny
zaczyna doznawać precesji.

Z drugiej strony pochodna momentu pędu względem czasu jest również równa momentowi sił zewnętrznych:

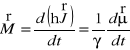
(11)

Porównując ze sobą oba wyrażenia otrzymujemy znane równanie ruchu precesyjnego momentu
po pobocznicy stożka precesji o stałym kącie rozwarcia:

(12)

Częstość precesji nosi nazwę częstości Larmoura i wynosi:

(13)

Rys.4. Precesja momentu magnetycznego
w polu magnetycznym o indukcji
.

Warunek rezonansu.

Jeżeli doznający precesji moment magnetyczny zostanie skierowana fala elektromagnetyczna (zwykle o częstotliwości mikrofalowej), której składowa magnetyczna
jest prostopadła do stałego pola
, oraz jej amplituda
, mogą zaistnieć warunki sprzyjające rezonansowej absorpcji energii prze układ stałe pole magnetyczne - moment magnetyczny. Składowa magnetyczną fali elektromagnetycznej
można rozłożyć na dwie składowe spolaryzowane kołowo, lecz o przeciwnych obiegach. Tylko składowa o obiegu zgodnym z obiegiem precesji daje ciągle działający moment skręcający w kierunku zwiększenia kąta precesji. Składowa o obiegu przeciwnym nigdy nie jest w fazie z precesja. Jeżeli częstość mikrofal
jest znacznie różni się od częstości precesji momentu magnetycznego
, to wpływ pola zmiennego
jest znikomo mały. Natomiast, jeśli wartość
jest bliska
, to pole zmienne
silnie działa na moment
powodując szybką zmianę w kierunku zwiększenia energii momentu
w polu
. Jest to efekt rezonansowego pochłaniania energii (Rys.5.b).Warunek rezonansu ma postać:

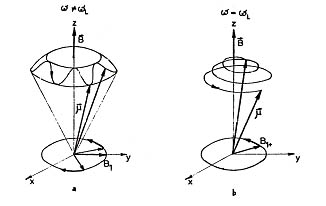
Rys.5. Precesja momentu magnetycznego
w polu magnetycznym o indukcji
i pod wpływem prostopadłej do niej składowej magnetycznej mikrofal
:

a)
, b)

Rozwiązanie równania ruchu. Kształt linii rezonansowej.

Na skutek oddziaływania momentów magnetycznych z siecią krystaliczną (zwykle między sobą oraz z najbliższym otoczeniem), energia będzie wyrównywać się w układzie spinów oraz będzie odpływać do sieci w ciągu skończonego czasu. Możemy wyróżnić:

-podłużny czas relaksacji
: są za niego odpowiedzialne ruchy termiczne cząsteczek lub atomów (czas relaksacji spin-sieć)

-poprzeczny czas relaksacji
: wynika z oddziaływania spinów między sobą (czas relaksacji spin-spin), jest mały i niezależny od temperatury

Procesy relaksacyjne powodują, że wektor
nie osiągnie płaszczyzny horyzontalnej, lecz jego położenie równowagowe ustali się w nowym kierunku, o większym rozwarciu stożka niż przed rezonansem. Wtedy tyle energii, ile układ pobierze w jednostce czasu, tyle samo straci na procesy relaksacyjne.

Uwzględnienie procesów relaksacyjnych w równaniu ruchu momentu magnetycznego w sumarycznym polu
dokonuje się przez dodanie tzw. wyrazu tłumiącego:

(14)

W wyniku rozwiązania równań ruchu po uwzględnieniu procesów relaksacyjnych otrzymujemy warunek rezonansu i kształt krzywej rezonansowej, tzn. zależność dynamicznej podatności magnetycznej od częstości mikrofal lub od pola

(15)

gdzie:

-
składowa dyspersyjna

-
składowa absorpcyjna

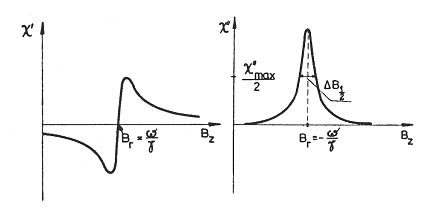
Rys.6. Zależność składowych dyspersyjnej
i absorpcyjnej
dynamicznej podatności od pola magnetycznego.

Tylko składowa absorpcyjna ma kształt rezonansowy, tak więc moc absorbowana przez próbkę z pola mikrofalowego jest proporcjonalna do

Kształt linii rezonansowej możemy wyrazić przez szerokość połówkową linii
, zdefiniowaną jak na Rys.6.

Spektrometr mikrofalowy mierzy nie krzywą absorpcyjną, lecz jej pierwszą pochodną (jak pokazuje Rys.7.), co spowodowane jest tzw. detekcją fazoczułą.

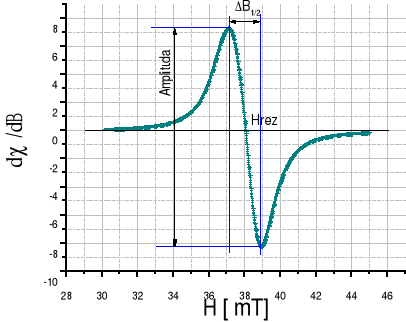
Rys.7. Krzywa rezonansowa - wykres zależności pochodnej składowej absorpcyjnej od przyłożonego pola magnetycznego.

Rezonans Ferromagnetyczny.

Składowe energii swobodnej ferromagnetyka.

W ferromagnetyku momenty magnetyczne są silnie sprzężone ze sobą. Z tego względu w równaniu ruchu uwzględniamy precesję nie oddzielnych momentów magnetycznych
, lecz wektora namagnesowania.

(16)

Pole magnetyczne występujące w równaniu ruchu jest całkowitym polem efektywnie działającym na moment magnetyczny, czyli pochodzi nie tylko od pola zewnętrznego
, ale także od tzw. pola wewnętrznego. Dlatego efektywne pole
w monokrystalicznym ferromagnetyku ma inny kierunek i wartość niż pole zewnętrzne.

Zgodnie z tym, co powiedziano wcześniej równanie ruchu ma postać:

(17)

i można wyrazić je jako zależność od całkowitej energii swobodnej ferromagnetyka, gdyż ma wtedy postać ogólniejszą. Musimy uwzględnić wszystkie przyczynki do energii swobodnej F, które zależą od kierunku wektora

(18)

gdzie:

- energia zeemanowska

-energia pola odmagnesowującego, zależy od kształtu próbki

-energia anizotropii magnetokrystalicznej

-energia wymienna

-energia ścian domenowych

-energia magnetoelastyczna

Zwykle uwzględnia się tylko pierwsze trzy wyrazy w wyrażeniu na energię, ponieważ
jest proporcjonalne do namagnesowania i nie zależy od kąta (jest izotropowe), gdy założymy, że nie występują kątowe niejednorodności przestrzenne namagnesowania,
jest zwykle zaniedbywanie mała, a
nie występuje, gdyż eksperyment prowadzimy zwykle w polach nasycających, w których nie ma struktury domenowej.

Warunek rezonansu dla monokryształu ferromagnetyka wzdłuż jego głównych osi krystalograficznych.

Energię swobodną uwzględnianą w równaniu ruchu możemy zapisać w formie:

(19)

gdzie:

;
- tensor czynnika odmagnesowania

-pole anizotropii w tzw. formie Kittela

- tensor czynników anizotropii

Wtedy:
(20)

Wstawiając odpowiednie wyrażenia na składowe namagnesowania oraz zakładając, że pole
skierowane jest np. wzdłuż osi y oraz zakładając, że jest ono na tyle silne, iż wektor
podąża za kierunkiem pola
otrzymujemy warunek rezonansu w formie:

(21)

gdzie:

-składowe tensora odmagnesowania

-składowe tensora czynników anizotropii

Zależność pola efektywnego od kształtu próbki.

Gdy założymy, że anizotropia krystaliczna jest mała w porównaniu z anizotropią kształtu, to:

1. Dla próbki kulistej:
   

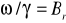
2. Dla dysku lub płaskiej płytki

-gdy pole B leży w płaszczyźnie próbki:

-gdy pole B przyłożymy prostopadle do płaszczyzny próbki:

3. Dla długiego walca

-pole równoległe do osi walca:

-pole prostopadłe do osi walca:

Rozwiązanie równań ruchu dla namagnesowania z uwzględnieniem tłumienia.

Kształt linii rezonansowej.

W rezonansie FMR najczęściej stosowany jest wyraz tłumiący zaproponowany przez Landaua i Lifszica. Równanie ruchu przyjmuje wtedy formę:

(22)

gdzie:
- bezwymiarowy parametr tłumienia

Kształt linii jest lorentzowski:

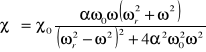
(23)

gdzie:

Szerokość linii wynosi:

Próbki metaliczne

Ze względu na efekt naskórkowy (wnikanie mikrofal w metal ma ograniczony zasięg), amplituda mikrofal maleje eksponencjalnie z odległością od powierzchni próbki, a głębokość wnikania δ dana jest wzorem:

(24)

gdzie:

-przenikalność magnetyczne próżni

σ-przewodnictwo właściwe próbki

Równanie ruchu magnetyzacji zawiera wtedy dodatkowy składnik - tzw. efektywne pole wymiany, dające dodatkowy moment skręcający w postaci:

(25)

gdzie:

- stała wymiany

- zmiana wektora
z odległością i jest duży, gdy głębokość wnikania jest mała.

Nierezonansowa absorpcja w diamagnetykach.

Absorpcja mikrofal ma również duże zastosowanie poza obszarem absorpcji rezonansowej - mówimy wtedy o absorpcji nierezonansowej. Klasycznym przykładem zastosowania tego zjawiska jest absorpcja w nadprzewodnikach poniżej temperatury krytycznej. Wówczas nadprzewodnik jest w stanie diamagnetycznym.

Typowe krzywe absorpcji nierezonansowej dla nadprzewodnika YbaCuO przedstawia rysunek xx.

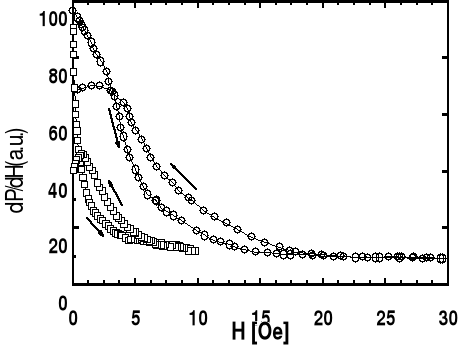
Bardzo interesujące są pomiary absorpcji mikrofalowej w cienkich warstw magnetycznych. Warstwy magnetyczne są które ze względu na ich zastosowanie, głównie jako nośniki pamięci. Anizotropia magnetyczna powoduje zmianę pola rezonansowego w bardzo szerokim zakresie (Rysunek.xx).

Struktura subtelna i nadsubtelna w ERP.

Źródłem rozszczepienia i tym samym absorpcji fal elektromagnetycznych może być również pole krystaliczne, które zachodzi nawet w zerowym polu magnetycznym. Tego typu rozszczepienie jest źródłem tzw. subtelnej struktury widm EPR. Pole krystaliczne oddziałuje na centrum paramagnetyczne o spinie S, który to spin oddziałuje również z momentem orbitalnym. Jako przykład podamy oddziaływanie pola krystalicznego ze spinem S=3/2 jonu chromu Cr³⁺. Zgodnie z regułą wyboru Δm_S=1, widmo struktury subtelnej będzie się składać z trzech linii (-1/2, 1/2, 3/2). Z tego widma można wyznaczyć parametr struktury subtelnej D,

który informuje o sile sprzężenia L-S w następujący sposób:

Struktura nadsubtelna widma EPR powstaje wówczas, gdy uwzględniamy dodatkowo oddziaływanie spinu elektronowego S ze spinem jądrowym I. Jako przykład można przytoczyć rozszczepienie jądrowego spinu I=3/2 izotopu chromu ⁵⁵Cr³⁺. Stan I=3/2 rozszcepia się na 2I+1 poziomów czyli na cztery podpoziomy, przy czym dla każdej lini struktury subtelnej mamy po cztery linie struktury nadsubtelnej, gdzyż obowiązuje reguła wyboru Δm_I=0.

EPR w substancjach napromienionych.

W badaniach EPR używa się często wnęki rezonansowej z przednią ścianką wyposażoną w szczeliny, co umożliwia naświetlanie próbki in situ bez zakłócania promieniowania mikrofalowego. W badaniach tych mamy na ogół do czynienia z fotolizą czyli z rozkładem cząsteczek związków chemicznych pod wpływem promieniowania ultrafioletowego oraz radiolizą, która zachodzi pod wpływem promieniowania o większej częstotliwości (jonizującego). Widma absorpcyjne pochodzą najczęściej od powstałych rodników lub od substancji, które powstawały w wyniku reakcji z tymi rodnikami. Foroliza i radioliza mają duże znaczenie w badaniach układów biologicznych.

W przypadku badania małych, wyizolowanych cząsteczek ważne znaczenia ma napromienianie falami X lub γ. Do związków będących często obiektami badań są m. in. aminokwasy, cukry, estry fosforanowe itp. Próbki przygotowywane są w postaci monokryształów, proszków, oraz rozcieńczonych roztworów ciekłych i stałych.

Budowa i zasada działania spektrometru mikrofalowego

Spektrometr składa się z trzech zasadniczych części:

• bloku mikrofalowego

• bloku pola magnetycznego

• bloku detekcji

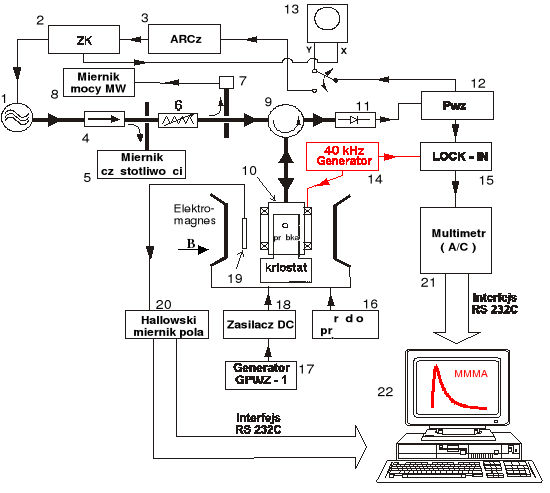
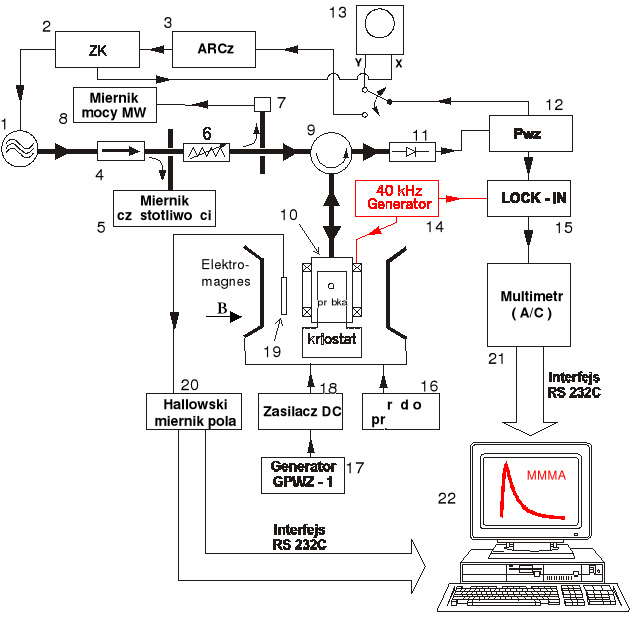
Rys.8. Schemat blokowy spektrometru mikrofalowego:

1 - klistron odbiciowy, 2 - zasilacz klistronu, 3 - układ automatycznej regulacji częstotliwości, 4 - izolator ferrytowy, 5 - cyfrowy miernik częstotliwości mikrofal, 6 - tłumik regulowany, 7 - termoelektryczna sonda mocy , 8 - cyfrowy miernik mocy, 9 - cyrkulator ferrytowy, 10 - cylindryczna wnęka mikrofalowa, 11 - głowica detekcyjna, 12 - przedwzmacniacz, 13 - oscyloskop, 14 - modulator 40 kHz zewnętrznego pola magnetycznego cewek modulujących do pomiaru MMMA, 15 - selektywny nanowoltomierz fazoczuły, 16 - zasilacz uzwojeń głównych elektromagnesu, 17 - generator linowych przebiegów wolnozmiennych, 18 - zasilacz cewek korekcyjnych elektromagnesu, 19 - głowica hallowska, 20 - cyfrowy miernik pola HTM11, 21 - multimetr cyfrowy METEX , 22 - komputer klasy AT 386.

Spektrometr pracuje w paśmie X mikrofal, czyli, tzn. od 8,0 GHz do 12 GHz, przy czym częstotliwość pracy wynosi zwykle ok. 9,5 GHz. Spektrometr jest typu odbiciowego, czyli mierzy się moc mikrofal odbitych od wnęki rezonansowej.

Blok mikrofalowy: generuje mikrofale, mierzy ich częstotliwość, reguluje moc, rozdziela mikrofale najpierw na próbkę do wnęki rezonansowej, a potem do diody detekcyjnej, przeprowadza detekcję mikrofal odbitych od wnęki, umożliwia obserwację modów generacji klistronu na oscyloskopie (w celu precyzyjnego zestrojenia wnęki z klistronem na jedną wybraną częstotliwość), oraz automatycznie dostraja częstotliwość klistronu do aktualnej częstotliwości wnęki za pomocą układu automatycznej regulacji częstotliwości (Arcz).

Blok pola magnetycznego: służy do wytworzenia pola magnetycznego
, które narasta automatycznie dzięki tzw. układowi przemiatania pola. W skład tego bloku wchodzi również hallowski miernik pola oraz układ modulacji stałego pola elektromagnesu przez sinusoidalnie zmienne pole magnetyczne, który jest potrzebny jako sygnał odniesienia do fazoczułej detekcji linii w bloku detekcji.

Układ modulacji pola magnetycznego składa się z modulatora oraz cewek modulacyjnych (zaprojektowanych w układzie Helmholtza), obejmujących z obu stron ścianki wnęki rezonansowej. Modulację stosuje się w celu zwiększenia stosunku sygnał/szum, zaś jej częstotliwość wynosi 40 kHz. Modulacja stałego pola powoduje modulację sygnału mikrofalowego odbitego od wnęki. Ponieważ dioda mierzy tylko obwiednię, otrzymujemy pierwszą pochodną krzywej absorpcji.

Blok detekcji służy do wykrycia, wzmocnienia i zmierzenia sygnału z diody mikrofalowej. Z uwagi na fakt, że sygnał EPR-owski jest dużo słabszy od różnego rodzaju zakłóceń korzystamy z techniki detekcji fazoczułej (technika LOCK-IN). Detekcja fazoczuła jest jedną z metod pomiarowych, która znajduje zastosowanie tam, gdzie dokonujemy pomiaru słabych sygnałów w obecności szumu. Aby rozróżnić użyteczny sygnał od wszelkich zakłóceń i wyodrębnić go, dokonujemy najpierw modulacji sygnału z określoną częstością: polega to na modulowaniu (przerywaniu) wzbudzenia lub modulowaniu parametrów pomiarowych.

Jeżeli założymy, że sygnał z generatora modulacji (sygnał odniesienia) ma zadaną częstość ω_mod i fazę q_ref, to obserwowany sygnał również będzie zawierał składową zmodulowaną o tej samej częstości, choć może o innej fazie: V_sigsin(ω_modt+q_sig). Układ detektora fazoczułego wykonuje matematyczną operację mnożenia sygnału przez sygnał odniesienia:

V_det = V_refsin(ω_modt+q_ref) · V_sigsin(ω_modt+q_sig).

Wykorzystując związek trygonometryczny sina · sinb = ½ cos (a+b) - ½ cos (a-b) dostajemy, że sygnał po przemnożeniu ma postać:

V_det = ½V_ref V_sig cos[q_sig - q_ref] - ½V_ref V_sig cos[2ω_mod t + q_sig + q_ref]

i zawiera składową stałą. Wystarczy zatem przepuścić ten sygnał przez filtr odcinający składowe zmienne i otrzymamy wyłącznie pierwszy wyraz, który jest proporcjonalny do wielkości mierzonego sygnału. Proszę zwrócić uwagę, że jedynie sygnał o częstości dokładnie równej częstości modulacji da nam wkład do V_det, szumy o wszystkich innych częstościach, różnych od częstości modulacji zostaną odcięte przez filtr i to nawet, gdy ich amplituda jest znacznie większa od amplitudy szukanego sygnału. Sygnał wyjściowy zależy od różnicy fazy między modulacją a rejestrowanym sygnałem, stąd nazwa detekcji fazoczułej.

Regulując układ detektora fazoczułego musimy dokonać nastawy parametrów: czułości, stałej czasowej i fazy. Czułość detektora to po prostu stopień wzmocnienia sygnału. Stała czasowa określa jak dobry jest filtr odcinający składowe zmienne; im dłuższa stała czasowa, tym mniej szumów, ale cały układ wolniej reaguje — należy zatem przeprowadzać pomiary bardzo wolno. Faza wreszcie ustala wartość (q_sig - q_ref), a co za tym idzie wielkość (i znak) sygnału wyjściowego.

Przygotowanie próbek.

Próbki substancji przeznaczone do badań w spektrometrach EPR mogą być ciekłe lub stałe - te ostatnie w postacji szkliw, proszków mikrokrystalicznych lub kryształów (monokryształów). Objętość próbki powinna być rzędu 0.2 cm³ lub rzędu od kilkudziesięciu do kilkuset mg. Zbyt duże próbki mogą obniżać czułość pomiaru, szczególnie w przypadku próbek będących roztworami wodnymi, które najlepiej badać w kapilarach lub tubkach o specjalnej konstrukcji, gdzie roztwór we wnęce rezonansowej stanowi cienką, płaską warstwę. Stężenie rodników w roztworach powinno być mniejsze niż 10^-4 mol/dm³, aby zapobiec poszerzeniom linii w wyniku oddziaływań spin-spin (tzw. poszerzenie wymienne). Aby unikać nakładania blisko leżących linii, należy usuwać rozpuszczony tlen, który, jako paramagnetyczny może również przyczyniać się do poszerzenia linii absorpcyjnej. W przypadku roztworów zamrożonych może następować rozdzielenie faz, szczególnie częste w układach wodnych, uniemożliwiające badania EPR. Za poszerzenie linii absorpcji może być odpowiedzialne również tworzenie się agregatów centrów paramagnetycznych.

Widma czystych, stałych substancji paramagnetycznych dają często szerokie, pojedyncze linie. Dzieje się tak dlatego, że niesparowane elektrony są blisko siebie i zachodzi wymiana spinów.

Przy badaniu monokryształów najłatwiej jest otrzymać precyzyjne wartości czynnika g ponieważ inne oddziaływania na ogół uśredniają się do zera.

W przypadku substancji ferromagnetycznych przygotowuje się próbki najczęściej w postaci cienkich prostopadłościanów lub też w postaci kulistej, przygotowywanych na specjalnych młynkach.

Interpretacja linii widmowych.

W większości spektrometrów otrzymujemy widma, które są pierwszą pochodną krzywej absorpcji, z której natychmiast otrzymujemy szerokość połówkową oraz pole rezonansowe z przecięcia widma z linią bazową. W przypadku małej rozdzielczości widma korzystnie jest rejestrować lub obliczyć drugą pochodną sygnału absorpcji, ponieważ składowe widma mogą wystąpić wyraźniej. Czasami stosuje się metodę wprowadzania śladowych ilości substancji wzorcowej do badanej próbki i prowadzi się jednoczesną rejestrację widma substancji badanej i wzorcowej. Często substancją wzorcową jest dwufenylopikrylohydrazyl (DPPH). Pole powierzchni pod krzywą rezonansową jest proporcjonalne do całkowitej liczby niesparowanych elektronów. W celu obliczania pól powierzchni wykorzystuje się programy komputerowe jak np. Origin. Jeśli występuje duży szum w rejestrowanych widmach, to konieczna jest wstępna jego obróbka mająca na celu ograniczenie szumów (tzw. smoothing). Przy analizowaniu krzywych Lorentza należy postępować ostrożnie, aby nie obciąć ich długich bocznych skrzydeł.

Pomiary EPR dają szerokie możliwości badawcze własności mikroskopowych jak również badań komplementarnych.

Z pomiarów EPR można wyznaczyć wartości główne czynnika Landego g oraz tensorów struktury subtelnej (oddziaływania pola krystalicznego ze spinem) oraz struktury nadsubtelnej (odziaływania spinu elektronowego ze spinem jądrowym).

Poprzez badanie zależności czasów relaksacji podłużnej i poprzecznej (T₁ i T₂) od temperatury i szerokości linii i tensora oddziaływania nadsubtelnego od temperatury i ciśnienia wnioskuje się o ruchach molekularnych wewnątrz sieci krystalicznych.

Bardzo duża czułość pomiarów EPR wykorzystuje się w wykrywaniu sadowych domieszek (centrów) paramagnetycznych w matyrycy niemagnetycznej. Badania te są użyteczne do analizy chemicznej i badania kinetyki reakcji chemicznych.

10

---