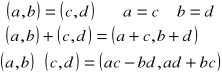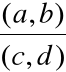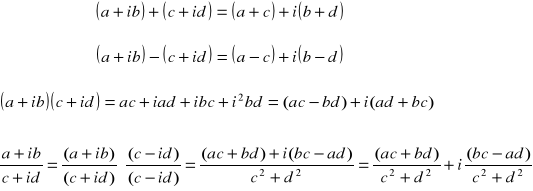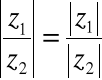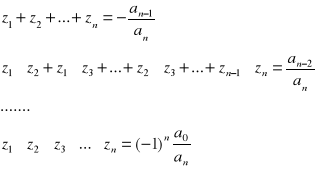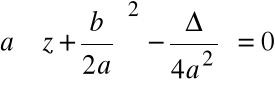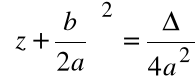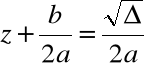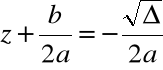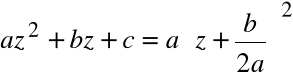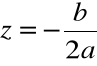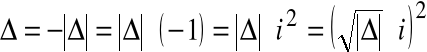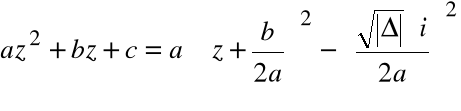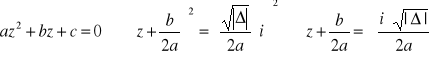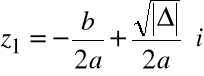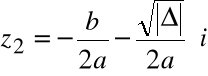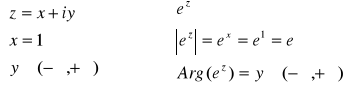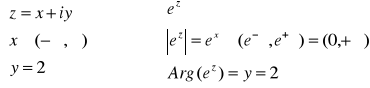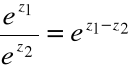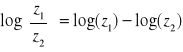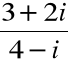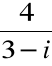WYKŁAD 2 |
LICZBY ZESPOLONE |
Niech a, b, c, d, ... będą elementami zbioru liczb rzeczywistych R. Wprowadzimy obecnie pewne
uogólnienie liczby rzeczywistej
Będzie nim uporządkowana para liczb rzeczywistych spełniająca pewne definicje i nazwana liczbą zespoloną.
Definicja
Liczbami zespolonymi nazywamy uporządkowane pary liczb rzeczywistych, np. (a, b), (c, d)…, dla których określamy równość, dodawanie i mnożenie
w sposób następujący:
|
Wynikiem dodawania i mnożenia liczb zespolonych są liczby zespolone, a więc są to działania wewnętrzne.
Przykład
Obliczyć sumę i iloczyn liczb zespolonych (2,-1) i (3,7)
(2, -1) + (3, 7) = (2 + 3, -1 + 7) = (5, 6)
(2, -1)(3, 7) =![]()
= (13, 11)
Zbiór liczb zespolonych oznaczymy literą C;
jest to początkowa litera łacińskiego słowa complexus
Zbiór liczb zespolonych jest ciałem liczbowym.
Definicja
Odejmowaniem liczb zespolonych
nazywamy działanie odwrotne do dodawania.
Wynik odejmowania liczb zespolonych nazywamy
różnicą liczb zespolonych.
(x,y) = (a,b) - (c,d) |
Z definicji dodawania i równości liczb zespolonych wynika, że wtedy x + c = a i y +d = b, czyli :
(a, b) - (c, d) = (a - c, b - d) |
Zatem odjęcie od siebie dwóch liczb zespolonych polega na odjęciu wartości odpowiednich współrzędnych.
Przykład
(2,-1) - (3,7) = (2 - 3, -1 - 7) = (-1,-8).
Definicja
Dzieleniem liczb zespolonych
nazywamy działanie odwrotne do mnożenia.
Wynik dzielenia liczb zespolonych nazywamy
ilorazem liczb zespolonych.
(x, y) =
|
Z definicji mnożenia i równości liczb zespolonych wynika, że wtedy: 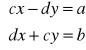
Mnożąc pierwsze równanie przez d a drugie przez c oraz odejmując pierwsze równanie od drugiego otrzymamy
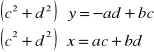
Układ ten jest zatem jednoznacznie rozwiązalny, gdy wartość ![]()
jest różna od zera, czyli gdy liczba zespolona (c, d)≠(0,0). Stąd:
|
Przykład
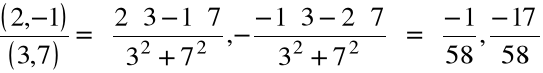
W zbiorze liczb zespolonych wyodrębniamy
zbiór elementów postaci: (a,0)
gdzie a jest dowolną liczbą rzeczywistą.
Zbiór ten utożsamiamy ze zbiorem liczb rzeczywistych.
Możemy tak zrobić dlatego, że działania na elementach (a,0) są analogiczne do działań na liczbach rzeczywistych:
|
(poprzedniki dodajemy i mnożymy jak liczby typu real )
W dalszym ciągu będziemy utożsamiali liczbę zespoloną (a,0) z liczbą rzeczywistą a, w szczególności liczba (0,0) będzie utożsamiana z zerem rzeczywistym.
|
|
Reprezentacje liczb zespolonych w postaci a+bi
Jedynka urojona
Liczby (0, b) różnej od zera zespolonego, nie można
w analogiczny sposób utożsamić z żadną liczbą rzeczywistą.
Definicja
Liczbę (0,1) będziemy oznaczać symbolem i :
i = (0,1)
Liczbę tę nazywamy jedynką urojoną
Urojona, dlatego że ![]()
= (-1,0) ≡ -1
gdyż ogólnie: ![]()
a w szczególności: ![]()
(0, 1)∙(0, 1)=(-1, 0)= -1
Zatem liczbę ![]()
utożsamiamy z liczbą -1
|
Pamiętamy że nie istnieje liczba rzeczywista,
której kwadrat byłby liczbą ujemną.
Ponieważ:
|
możemy liczbę zespolona (a,b) utożsamiać z wyrażeniem: a+bi zwanym
postacią kanoniczną Gaussa liczby zespolonej (a,b)
W wyrażeniu a+bi wprowadzamy nazwy:
![]()
- część rzeczywista ![]()
- część urojona
a = Re(a + bi), Re - realis - rzeczywisty (łac.)
b = Im(a + bi), Im - imaginarius - urojony (łac.)
Liczba zespolona ib, gdy ![]()
- liczba urojona.
Liczbę zespoloną będziemy dalej nazywać krótko liczbą i oznaczać także jedną litera, np. z, gdzie z = a + bi.
Działania na liczbach zespolonych w postaci kanonicznej
|
Definicja
Modułem liczby zespolonej z = a + bi, oznaczanym przez ![]()
, nazywamy rzeczywistą liczbę nieujemną, będącą pierwiastkiem sumy kwadratów części rzeczywistej i części urojonej tej liczby
![]()
Przykład
![]()
Stwierdzenie
Liczba zespolona jest wtedy i tylko wtedy zerem,
gdy jej moduł jest równy zeru z=0![]()
![]()
=0
Definicja
Liczbą sprzężoną z liczbą ![]()
nazywamy liczbę postaci ![]()
Definicja
Dwie liczby, z których jedna jest sprzężona z drugą, nazywamy liczbami sprzężonymi.
Stwierdzenie
|
|
Wzór (ii) można napisać w postaci
|
Wniosek
W zbiorze liczb zespolonych sumę kwadratów można rozłożyć na iloczyn czynników pierwszego stopnia.
Przykład
![]()
Stwierdzenie
Liczba odwrotna do liczby zespolonej ma postać
![]()
dla ![]()
Iloraz liczb zespolonych ma postać
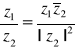
dla ![]()
Przykład
Z pierwszej równości ostatniego stwierdzenia
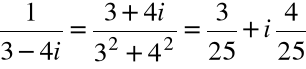
Z drugiej równości ostatniego stwierdzenia
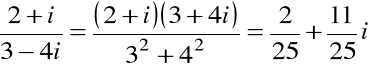
Przykład
Rozwiązanie równania kwadratowego dla ![]()
![]()
![]()
![]()
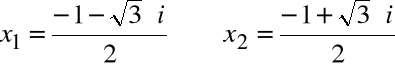
INTERPRETACJA GEOMETRYCZNA LICZB ZESPOLONYCH
Diagram Arganda
Interpretacje liczby zespolonej:
![]()
punkt P(x, y) - diagram Arganda
Liczbę zespoloną z = x + yi możemy interpretować jako:
punkt P(x,y) na płaszczyźnie
wektor [x,y] o początku w punkcie P(0,0)
i o końcu w punkcie P(x,y)
Płaszczyznę zespoloną oznaczymy symbolem C.
Y
X
Oś rzeczywista =Re(z)
Geometryczna interpretacja działań
dla liczb zespolonych
Dodawanie liczb zespolonych = dodawanie wektorów
![]()
Odejmowanie liczb zespolonych =odejmowanie wektorów
![]()
Imz
z1-z2 z1 z1+z2
z2
Rez
- z2
Definicja
Argumentem liczby ![]()
, oznaczanym przez Arg (z), nazywamy każdą liczbę rzeczywistą ![]()
, spełniającą dwa warunki:
|
|
Uwaga: Argument liczby 0 nie jest określony.
Definicja
Argument główny liczby z - argument liczby z,
który należy do przedziału ![]()
.
Oznaczenie: Arg(z)
Stąd ![]()
< Arg(z) ![]()
oraz arg(z) = Arg(z) + ![]()
, ![]()
±1,...
Przykład
Arg(1) = 0, arg(1) =![]()
, Arg(i) =![]()
/2, arg(i) = ![]()
/2 +![]()
Moduł liczby zespolonej -długość wektora wodzącego punktu odpowiadającego tej liczbie
Argument liczby zespolonej - miara względna kąta,
jaki tworzy wektor wodzący punktu z z osią rzeczywistą
Im(z)
z=x+yi
r=|z|
Re(z)
0
Z rysunku wynika, że liczbę zespoloną z możemy utożsamiać z parą ![]()
, gdzie φ jest argumentem głównym z.
Takie przedstawienie nazywa się często przedstawieniem we współrzędnych biegunowych
Kąt φ jest kątem skierowanym:
Dodatnim w kierunku przeciwnym do wskazówek zegara,
Ujemnym w kierunku zgodnym ze wskazówkami zegara,
Postać trygonometryczna liczby zespolonej
|
r - moduł liczby zespolonej
|
Przykład
Zapisać w postaci trygonometrycznej liczbę ![]()
posługując się jej głównym argumentem.
![]()
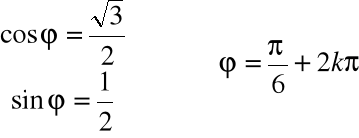
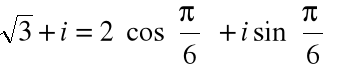
Im(z)
z=
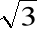
+i
r=2
ϕ=π/6
![]()
Re(z)
Definicja
Równość dwóch liczb zespolonych w postaci trygonometrycznej

i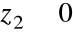

![]()
Uwaga
Zapis arg z![]()
arg z![]()
(mod 2![]()
)oznacza, że argumenty liczb
z![]()
i z![]()
są równe modulo 2![]()
tzn. argz![]()
argz![]()
+k2![]()
Mnożenie liczb zespolonych w postaci trygonometrycznej
![]()
, ![]()
![]()
![]()
=
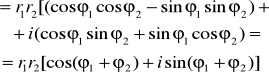
Dzielenie liczb zespolonych w postaci trygonometrycznej
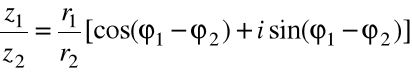
Wnioski
1 |
Moduł iloczynu dwóch liczb zespolonych jest równy iloczynowi ich modułów
|
2 |
Argument iloczynu dwóch liczb zespolonych jest równy sumie ich argumentów
|
3 |
Moduł ilorazu liczb zespolonych jest równy ilorazowi ich modułów
|
4 |
Argument ilorazu dwóch liczb zespolonych jest równy różnicy ich argumentów
|
Twierdzenie ( de Moivre'a)
|
Potęgowanie liczb zespolonych
Dla każdej liczby zespolonej ![]()
oraz dla liczby naturalnej ![]()
zachodzi:
|
Powyższe twierdzenie zachodzi również dla liczb całkowitych ujemnych:
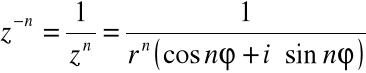
=
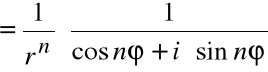
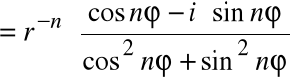
![]()
W szczególności, dla: ![]()
![]()
PIERWIASTKOWANIE LICZB ZESPOLONYCH
Funkcja: pierwiastek stopnia n
Definicja
Rozwiązania równania: ![]()
gdzie ![]()
oraz ![]()
;
nazwiemy pierwiastkami stopnia n z liczby ![]()
.
Twierdzenie
Pierwiastków stopnia n z liczby zp jest n |
Wniosek
Zapis
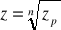
dla liczby z nie jest jednoznaczny.
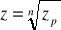
nie jest funkcją jednoznaczną
Rozwiązanie równania: ![]()
dla trygonometrycznej postaci liczb zespolonych:
![]()
![]()
Z twierdzenia de Moivre'a:
![]()
otrzymujemy:
(1) ![]()
![]()
![]()
(2) ![]()
(3) ![]()
Układ równań (2),(3) ma rozwiązanie postaci:
![]()
czyli ![]()
gdzie ![]()
Stąd:
|
|
Łatwo zauważyć że jeśli ![]()
.
Zatem otrzymujemy n różnych wartości ![]()
,
numerowanych przez liczby ![]()
.
Pierwszy pierwiastek ( dla liczby k=0 )
|
nazywamy pierwiastkiem głównym
Przykład
![]()
dwa pierwiastki stopnia 2 z liczby ![]()
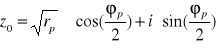
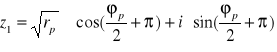
Można udowodnić że ![]()
Interpretacja geometryczna pierwiastków
![]()
Pierwiastki stopnia n są położone w wierzchołkach
n-kąta foremnego wpisanego w okrąg o środku (0, 0).
i promieniu ![]()
Zastosowanie Liczb Zespolonych.
Liczby zespolone wykorzystuje się w matematyce,fizyce, elektrotechnice (obwody prądu zmiennego).
FUNKCJE ZMIENNEJ ZESPOLONEJ |
Wielomiany :
![]()
Własności wielomianów
Dwa wielomiany możemy podzielić przez siebie z resztą lub bez reszty.
Twierdzenie o podzielności wielomianów
Dla każdej pary wielomianów W(z) i P(z) gdzie stopień P(z)>0, istnieją wielomiany Q(z) i R(z) takie, że:
|
stopień R(z) < stopień P(z) |
Powyższe przedstawienie jest jednoznaczne.
Wielomian Q(z) nosi nazwę ilorazu, a R(z) jest resztą.
Jeżeli R(z) = 0 dla każdego ![]()
to mówimy, że wielomian W jest podzielny przez wielomian P.
Przykład
Niech: ![]()
Wówczas: ![]()
Dzielenie wielomianu polega na sukcesywnym eliminowaniu najwyższych potęg wielomianu W(z).
W powyższym przykładzie ![]()
eliminuje
(po odjęciu) wyraz ![]()
wielomianu W(z)
![]()
Iloczyn ![]()
eliminuje wyraz ![]()
w reszcie.
Mamy zatem: ![]()
Ponieważ wynik odejmowania jest wielomianem stopnia 0, wzór daje wynik dzielenia W(z) przez P(z).
Ważny przypadek dzielenia wielomianów występuje gdy P(z) jest wielomianem st. 1, tzn. P(z) = z-a
Prawdziwe jest wówczas twierdzenie Bezout.
Twierdzenie Bezout
Resztą z dzielenia W(z) przez (z-a) jest W(a)
|
Liczba a jest pierwiastkiem wielomianu W(z)
wtedy i tylko wtedy gdy
|
|
Twierdzenie
Jeśli wielomian
![]()
jest wielomianem zmiennej zespolonej, to ![]()
możemy zapisać w postaci:
![]()
gdzie ![]()
i ![]()
są wielomianami o współczynnikach rzeczywistych od zmiennych x i y.
Dowód
Z równości : ![]()
, ![]()
, ![]()
, ![]()
,...
oraz z definicji dodawania i mnożenia.
Przykład
![]()
![]()
![]()
![]()
![]()
Wniosek
Ponieważ:
![]()
![]()
![]()
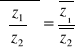
to dla wielomianu o współczynnikach rzeczywistych zachodzi: ![]()
czyli ogólnie: ![]()
Twierdzenie
Jeśli
o wspólczynnikach rzeczywistych to liczba sprzężona
|
Krócej: |
Dowód
Dla ![]()
mamy:
![]()
oraz ![]()
Stąd: ![]()
![]()
Przykład
Znaleźć wszystkie pierwiastki wielomianu
![]()
wiedząc, że jednym z nich jest ![]()
.
Rozwiązanie:
Ponieważ ![]()
jest pierwiastkiem równania również liczba do niego sprzężona 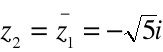
jest jego pierwiastkiem.
Z twierdzenia Bezout wynika, że wielomian w(z)
jest podzielny przez:
![]()
Iloraz z dzielenia wielomianu w(z) przez ![]()
wynosi
![]()
Wystarczy zatem rozwiązać równanie:
![]()
aby otrzymać ostatnie pierwiastki wielomianu w(z):
![]()
Uwaga
Z poprzednich twierdzeń wynika, że wielomian stopnia nieparzystego ma zawsze pierwiastek rzeczywisty.
Tak jest w istocie, ponieważ z faktu, że sprzężenie pierwiastka jest pierwiastkiem wynika, że liczba pierwiastków zespolonych jest parzysta.
Twierdzenie (zasadnicze twierdzenie algebry)
Każdy wielomian stopnia naturalnego n o współczynnikach zespolonych ma n pierwiastków w dziedzinie zespolonej |
W jego postaci iloczynowej występują tylko czynniki liniowe.
![]()
Generalnie nie wszystkie pierwiastki są różne i wtedy krotność niektórych pierwiastków jest większa od 1.
![]()
gdzie ![]()
to krotności poszczególnych pierwiastków spełniające równanie:
![]()
Opierając się na postaci iloczynowej wielomianu można pokazać że spełnione są wzory Viete'a:
|
Uwaga:
W dziedzinie rzeczywistej ogólna postać iloczynowa może zawierać oprócz czynników liniowych również czynniki kwadratowe nierozkładalne w R czyli czynniki postaci :
![]()
W praktyce zachodzi potrzeba badania krotności pierwiastków wielomianu. Można przy tym wykorzystywać twierdzenie Bezout'a lub wykorzystać własności różniczkowania wielomianu.
Liczba z0 jest k-krotnym pierwiastkiem wielomianu
W(z0) = 0, W'(z0) = 0, W''(z0) = 0, … W(k-1)( z0) = 0 i W(k)(z0) ≠ 0
|
gdzie W(k)(z0) oznacza pochodną rzędu k wielomianu W dla z0.
Twierdzenie
Każdy wielomian kwadratowy o współczynnikach rzeczywistych postaci:
W(z) = ![]()
ma w zbiorze C liczb zespolonych dwa pierwiastki
z1, z2 przy czym ma miejsce trychotomia:
|
Dowód
Postać kanoniczna wielomianu
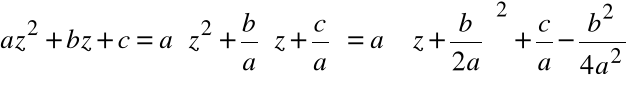
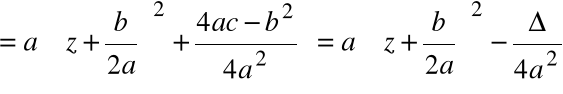
gdzie ![]()
1.
|
2.
|
3.
W zbiorze liczb zespolonych zachodzi:
Zatem:
Dwa pierwiastki zespolone
|
Przykład Rozwiązać równanie: ![]()
Ponieważ ![]()
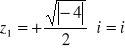
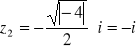
Uogólnienie powyższego twierdzenia jest następujące:
Każdy wielomian kwadratowy o współczynnikach zespolonych postaci: W(z) = ma w zbiorze C liczb zespolonych dwa pierwiastki z1, z2 :
a
W tym przypadku w ogólności bo współczynniki są zespolone a nie rzeczywiste. Jeżeli współczynniki będą rzeczywiste (bez części urojonej)
to oczywiście zachodzi:
|
♦Rozkład funkcji wymiernej właściwej na ułamki
proste w dziedzinie zespolonej.
Funkcja wymierna to funkcja będąca ilorazem dwóch wielomianów:
![]()
określona dla wszystkich liczb zespolonych nie będących pierwiastkami wielomianu P(z).
Jeżeli stopień W(z) >= stopień P(z) wtedy funkcję wymierną nazywamy niewłaściwą.
Jeżeli stopień W(z) < stopień P(z) wtedy funkcję wymierną nazywamy właściwą
Jeżeli stopień wielomianu W(z) jest wyższy od stopnia wielomianu P(z) to wówczas możemy wykonać dzielenie wielomianów i uzyskujemy postać:
![]()
gdzie :
R(z) jest tożsamościowo równy zero, albo
stopień R(z) < stopień P(z)
Wówczas funkcja R(z)/P(z) jest funkcją wymierną właściwą, którą można przedstawić jako sumę ułamków prostych.
Postać tych ułamków można wypisać po przedstawieniu P(z) w postaci iloczynowej:
![]()
Czynnikowi ![]()
odpowiada suma
ułamków prostych pierwszego rodzaju postaci:
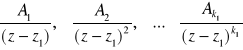
..........
Czynnikowi ![]()
odpowiada suma ułamków prostych I rodzaju postaci
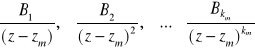
Przykład:
Rozłożyć na ułamki proste funkcję wymierną:
![]()
Funkcja podana jest już funkcją wymierną właściwą zatem nie wykonujemy dzielenia wielomianów lecz od razu wypisujemy ułamki proste zgodnie z ogólną teorią:
![]()
Dodając ułamki po prawej stronie i sprowadzając do mianownika takiego jak po lewej stronie możemy porównać liczniki:
![]()
Porównanie daje wartości stałych A, B, C, D:
A = -2, B = -i, C = 2, D = 3i
♦Rozkład funkcji wymiernej właściwej na ułamki
proste w dziedzinie rzeczywistej
Dla niektórych wielomianów uzyskamy rozkład na czynniki liniowe i wówczas postępujemy podobnie
jak dla dziedziny zespolonej.
Jednakże dla niektórych wielomianów w postaci iloczynowej mogą wystąpić czynniki kwadratowe nierozkładalne w dziedzinie rzeczywistej:
![]()
Z takimi czynnikami związane są ułamki proste II rodzaju postaci:
![]()
Zatem w rozkładzie wystąpią:
ułamki proste I rodzaju związane z czynnikami liniowymi
ułamki proste II rodzaju związane z czynnikami kwadratowymi nierozkładalnymi w dziedzinie rzeczywistej.
Przykład:
Rozłożyć na ułamki proste funkcję wymierną:
![]()
Zauważamy że jest to funkcja wymierna właściwa i przedstawiamy jej mianownik w postaci iloczynowej:
![]()
W postaci iloczynowej występuje:
czynnik liniowy (x+3)
czynnik kwadratowy
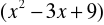
nierozkładalny w R (delta<0)
zatem wystąpią ułamki proste I i II rodzaju:
![]()
Sprowadzając do wspólnego mianownika i porównując ułamki dostajemy:
A = -1, B = 1, C = 4
FUNKCJA LINIOWA
f : C → C
![]()
gdzie:
![]()
= ![]()
![]()
![]()
Zobaczmy jaki jest wynik iloczynu :

![]()
Zatem iloczyn odpowiada wydłużeniu ![]()
oraz obrotowi o kąt (![]()
)
Zobaczmy jaki jest wynik dodawania:
![]()
![]()
Zatem dodawanie odpowiada translacji o wektor [c,d]Interpretacja geometryczna
(złożenie trzech przekształceń w płaszczyźnie )
(i) Wydłużenie(skrócenie) w stosunku ![]()
(ii) Obrót o kąt ![]()
(iii) Przesunięcie o wektor odpowiadający ![]()
Y
[c,d]
![]()
![]()
(rx,ry)
![]()
(x,y)
0 X
Przykład:
Znaleźć obraz prostokąta o wierzchołkach ![]()
w przekształceniu liniowym ![]()
Ponieważ ![]()
więc z ogólnej teorii wynika że przekształcenie to składa się z trzech przekształceń elementarnych:
wydłużenia w skali
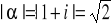
obrotu o kąt
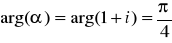
przesunięcia o wektor
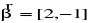
A zatem obrazem prostokąta jest prostokąt. Żeby precyzyjnie wyznaczyć jego
położenie na płaszczyźnie zespolonej można analitycznie okreslić
wierzchołki prostokąta po przekształceniu:
![]()
![]()
![]()
![]()
FUNKCJA WYKŁADNICZA: f(z) = ez
Definicja
Dla z = x + iy, przyjmiemy (wzory Eulera)
|
|
Stąd:
|
|
Zaobserwujmy interpretację geometryczną przekształcenia f(z) = ez.
Prześledzimy jak zmienia się w tym przekształceniu kwadrat na płaszczyźnie zespolonej:
![]()
Kwadrat ten jest częścią wspólną pasa nieskończonego ograniczonego prostymi x = 1 i x = 2 oraz pasa nieskończonego ograniczonego prostymi y = 2 i y = 3.
Zobaczmy najpierw jak przekształca się prosta x = 1.
|
A zatem obrazem prostej x = 1 jest okrąg o promieniu e.
Obrazem prostej x = 2 jest okrąg o promieniu e².
Wobec tego pas nieskończony zawarty między x = 1 i x = 2 przechodzi w pierścień kołowy o promieniach e i e².
Zobaczmy teraz jak przekształca się prosta y = 2.
|
Zatem obrazem prostej y = 2 jest półprosta o początku w punkcie (0,0) bez tego początku i nachyleniu 2 rad(1 rad≈57º).
Obrazem prostej y = 3 jest półprosta o początku w punkcie (0,0)
bez tego początku i nachyleniu 3 rad (1 rad≈57º).
Wobec tego pas nieskończony zawarty między y = 2 i y = 3 przechodzi w obszar zawarty między ramionami kąta o nachyleniu
2 rad i 3 rad.
Podsumowując kwadrat D= [1,2]x[2,3] przechodzi w przekształceniu
f(z)=ez w wycinek pierścienia kołowego D' o promieniach e i e² zawarty miedzy promieniami o nachyleniu 2 rad i 3 rad.
Własności funkcji f(z) = ez
Funkcja ez jest funkcją okresową tzn.:
|
Funkcja wykładnicza a pierwiastki stopnia n
Pamiętamy że pierwiastkowanie w dziedzinie zespolonej
nie jest jednoznaczne - istnieje n pierwiastków stopnia n:
![]()
numerowanych przez liczby ![]()
.
Wzór na k-ty pierwiastek:
![]()
Jeżeli k-ty pierwiastek przedstawimy w postaci wykładniczej korzystając ze wzoru Eulera i z własności funkcji wykładniczej to:
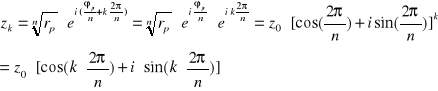
A więc k-ty pierwiastek możemy wygenerować z pierwiastka głównego poprzez pomnożenie go przez k-tą potęgę liczby:
![]()
Punktem startowym do generacji kolejnych pierwiastków
nie musi być pierwiastek główny, bowiem zachodzi również:
![]()
Wzór ten jest szczególnie użyteczny gdy chcemy przedstawić pierwiastki stopnia n w postaci kanonicznej.
Przykład:
Wyznaczyć ![]()
Zauważamy że jednym z pierwiastków jest liczba
![]()
Zatem następny pierwiastek da się obliczyć jako:
![]()
a następny czyli ostatni:
![]()
FUNKCJA LOGARYTMICZNA: f(z) = log(z) = ln(z)
Definicja
|
Uwaga: log(z) nie jest funkcją jednoznaczną ponieważ
dla ![]()
otrzymujemy:
![]()
Funkcja log(z) ma nieskończenie wiele gałęzi:
każdej ustalonej wartości k odpowiada jedna gałąź logarytmu będąca funkcją w dotychczasowym naszym rozumieniu tego terminu.
Gałąź główna: |
Zaobserwujmy jak funkcja log(z) przekształca wycinek pierścienia kołowego o promieniach e i e² zawartego między promieniami o nachyleniach 2 rad i 3 rad.
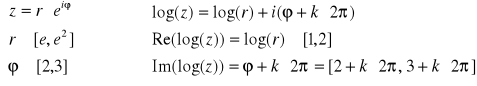
Tak więc obrazem wycinka pierścienia kołowego o promieniach e i e² zawartego między promieniami o nachyleniach 2 rad i 3 rad jest nieskończenie wiele kwadratów [1,2]x[2,3] przesuniętych
wzdłuż osi OY o wielokrotność 2π.
Własności funkcji log(z)
|
Możemy też zdefiniować w zbiorze C dowolną potęgę liczby :
|
Dowód:
Dla ![]()
, ![]()
mamy:
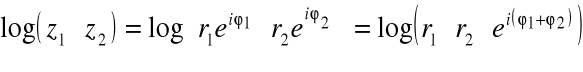
![]()
![]()
![]()
Ponadto:
![]()
.
Zadania
1. Obliczyć
a)
b)
c)
d)
|
2. Niech liczba
a liczba
Czy wynik jest zgodny z wynikiem b)
|
3. Korzystając z przedstawienia geometrycznego liczb zespolonych, uzasadnij kiedy
|
4. Rozwiąż równanie w dziedzinie zespolonej:
|
Poszukiwanie miejsc zerowych wielomianów
- algorytmy pierwiastnikowe
Algorytm Ferro, Tartaglii - wielomiany stopnia 3
|
Algorytm Ferrari - wielomiany stopnia 4
|
Twierdzenie Nielsa Abela i Evarista Galois Dla wielomianów stopnia ≥ 5 nie istnieje algorytm pierwiastnikowy
|
Algorytm poszukiwania zer wielomianu stopnia 3
![]()
Założenie: ![]()
,
jeśli nie - dzielimy obie strony równania przez ![]()
. 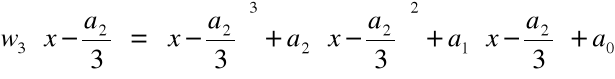
= 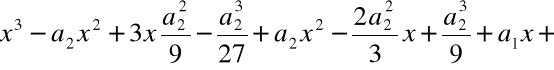
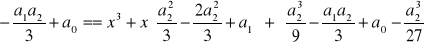
Założenie: ![]()
Krok 1. Szukamy zera wielomianu w postaci:
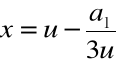
dla pewnego u![]()
Stąd 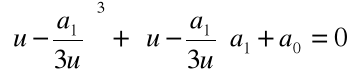
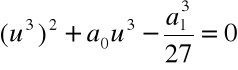
Krok 2. Przyjmujemy ![]()
i rozwiązujemy równanie
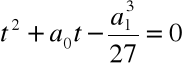
Rozwiązanie równania:
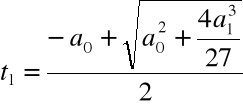
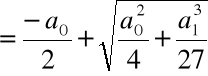
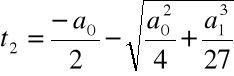
Krok 3. Wyliczamy
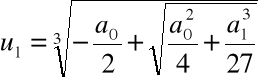
, 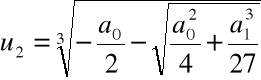
Krok 4. Wyliczamy 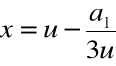
.
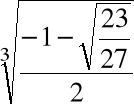
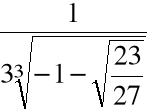
Przykład
Obliczyć pierwiastki wielomianu ![]()
= x3 -x+1
za pomocą algorytmu pierwiastkowego
Krok 1. Szukamy zer wielomianu w postaci:
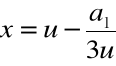
dla pewnego u![]()
a1= -1 zatem: 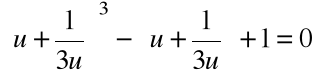
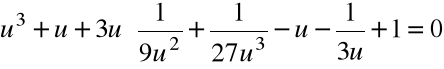
Po redukcji: 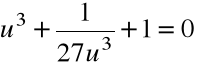
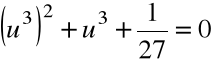
Krok 2. Przyjmujemy ![]()
i rozwiązujemy równanie:
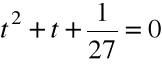
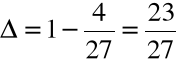
, 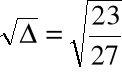
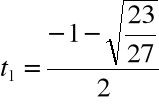
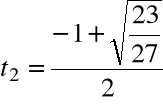
Krok 3. Wyliczamy
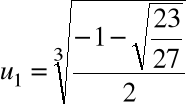
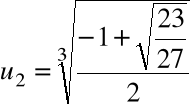
Krok 4. Wyliczamy 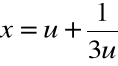
.
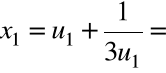
+
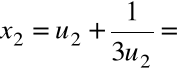
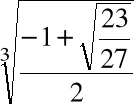
+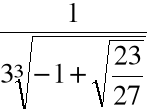
Algebra Liniowa z Geometrią
47
z=x+yi
P(x,y)
[x,y]
1
0
i
1
Oś urojona =Im(z)
Wyszukiwarka