POLITECHNIKA LUBELSKA

Katedra Sieci Elektrycznych i Zabezpieczeń

LABORATORIUM

SYSTEMÓW KOMPUTEROWYCH

TEMAT ĆWICZENIA:

OBLICZENIA ZWARCIOWE W PROGRAMIE SCC.

Skład grupy: Data wykonania

Sierota Krzysztof ED 8.5 2006.05.20

Misztal Małgorzata ED 8.5

1. Cel ćwiczenia.

Wykonanie 10 praktycznych ćwiczeń w modelu sieci elektroenergetycznej. Zadaniem pierwszych dziewięciu ćwiczeń było sprawdzenie umiejętności posługiwania się programem oraz znajomości teorii dotyczącej obliczeń zwarciowych. Natomiast dziesiąte ćwiczenie było zadaniem projektowym dotyczącym problemów rozwiązywanych w codziennej praktyce projektowania systemu elektroenergetycznego. Zadany węzeł URS 212, zadana linia LIN12.

2. Schemat badanego systemu energetycznego.

3. Ćwiczenie 1

Warunki zwarciowe w sieci są ciężkie ponieważ wszystkie punkty gwiazdowe transformatorów są uziemione, w wyniku czego prąd zwarcia doziemnego będzie miał duże wartości. Ponadto w układzie występuje dość dużo połączeń, które przy „zwinięciu” schematu można uznać za połączenie równoległe, a co za tym idzie impedancja zwarciowa maleje.

4. Ćwiczenie 2

Oznaczenia symboli:

S_zw - moc zwarciowa podana w MVA;

I_3F - prąd zwarcia trójfazowego podany w A;

I_2F - prąd zwarcia dwufazowego podany w A;

I_1F - prąd zwarcia jednofazowego podany w A;

3I0 - trzykrotna wartość prądu składowej zerowej podana w A;

Z₁ - impedancja zwarciowa dla składowej zgodnej podana w Ω;

Z₀ − impedancja zwarciowa dla składowej zerowej podana w Ω.

W nawiasach oznaczenia wg. IEC.

U _N = 220 kV; Z₁ = 49,75 Ω, Z₀ = 32,52 Ω, Z₀/Z₁ = 0,065

I _3F (I _K3”) =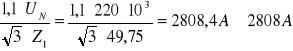

I _2F (I _K2”) =

I _1F (I _K1”) =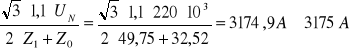

3 · I ₀ = I _1F = 3175 A

S _ZW­ (S _KQ”) =

Tabela porównawcza

Wielkość wyznaczana	Jednostka	Wyniki uzyskane w programie SCC	Wyniki obliczeń na podstawie wzorów
I 3F	[A]	2808	2808
I 2F	[A]	2432	2432
I 1F	[A]	3175	3175
3 I 0	[A]	3175	3175
S ZW	[MVA]	1070	1070

Na podstawie wykonanych obliczeń stwierdzam, że wyniki uzyskane na podstawie obliczeń po zaokrągleniu do części całkowitych jednostek, w jakich są podawane wyniki w programie SCC pokrywają się z wynikami uzyskanymi za pomocą tego programu. Program SCC zaokrągla wyniki obliczeń zwarciowych do wartości całkowitych.

5. Ćwiczenie 3

• Zwarcie trójfazowe

• Zwarcie dwufazowe faz B i C

• Zwarcie dwufazowe z ziemią faz B i C

• Jednofazowe zwarcie z ziemią fazy A

• Uwagi:

Wyniki dla zwarcia dwufazowego z ziemią uzyskane za pomocą opcji:

Obliczenia → Obrazy fazowe prądów → Na szynach rozdzielni

6. Ćwiczenie 4

Węzły, w których spełniona jest relacja I _1F > I _3F oraz I _2F > I _3F to: BRZ211, BUJ111, KUL212, LAG111, LAG211, UJA212, URS212, URZ211, URZ111, WOL111.

Są to węzły, do których poprzez transformatory z uziemionym punktem neutralnym przyłączone są generatory. Jedynym wyjątkiem jest węzeł WOL111,w którym znajduję się transformator 110 kV/SN i który jest przyłączony poprzez linię LIN27 o długości 8,75 km do węzła URZ111. W węźle ZLP111 jest spełniony warunek I _2F > I _3F, węzeł ten łączy się przez linię LIN24 o długości 8,75 km z węzłem LAG111.

Wynika z tego, że nierówności I _1F > I _3F lub I _2F > I _3F mogą być spełnione tylko w węzłach, w których poprzez transformator z uziemionym punktem neutralnym jest przyłączony generator oraz ewentualnie w węzłach przyłączonych do takiego węzła za pomocą względnie krótkiego odcinka linii. W pozostałych węzłach prąd I _3F jest największy, przy czym w większości z nich stosunki między prądami układają się następująco I _3F > I _2FG > I _1F > I _2F.

Jedynymi wyjątkami są węzły ZAL212 i NAR211, w których stosunki między prądami są następujące I _3F > I _2FG > I _2F > I _1F, są to linie pracujące na napięciu 220 kV, połączone z innymi węzłami za pomocą linii o długości ponad 130 km.

7. Ćwiczenie 5

• Zwarcie trójfazowe w węźle URS212 I _3F = 2808 A.

− udział od węzła BOR212 1344 A;

− udział od transformatora URS - T1 1465 A;

− razem 2809 A.

Różnica wyników równa 1 A wynika z zaokrągleń arytmetyki zmiennopozycyjnej komputera.

• Zwarcie dwufazowe w węźle URS212 I _2F = 2432 A.

− udział od węzła BOR212 1164 A;

− udział od transformatora URS - T1 1268 A;

− razem 2432 A.

• Zwarcie jednofazowe w węźle URS212 I _1F = 3175 A.

− udział od węzła BOR212 1170 A;

− udział od transformatora URS - T1 2005 A;

− razem 3175 A.

• Moc zwarciowa w węźle URS212 S _ZW = 1070 MVA.

− udział od węzła BOR212 512 MVA;

− udział od transformatora URS - T1 558 MVA;

− razem 1070 MVA.

• Impedancja dla składowej zgodnej przy zwarciu w węźle URS212 Z ₁ = 49,75 Ω.

− impedancja „widziana” od strony linii LIN12 103,9 Ω;

− impedancja „widziana” od strony transformatora URS - T1 95,4 Ω;

− razem 103,9 || 95,4 = 49,73 Ω.

Różnica wyników równa 0,02 Ω wynika z zaokrągleń arytmetyki zmiennopozycyjnej komputera.

Symbol || oznacza równoległe połączenie impedancji.

• Impedancja dla składowej zerowej w węźle URS212 Z ₀ = 32,5 Ω.

− impedancja „widziana” od strony linii LIN12 218,4 Ω;

− impedancja „widziana” od strony transformatora URS - T1 38,2 Ω;

− razem 218,4 || 38,2 =32,5 Ω.

• Wnioski:

Różnice pomiędzy wynikami otrzymanymi z programu SCC a wynikami obliczonymi są nieznaczne i wynikają z zaokrągleń arytmetyki zmiennopozycyjnej komputera. W przypadku naszego węzła URS212 są one nieznaczne a wpływ na większe rozbieżności ma ilość przyłączonych elementów do węzła. W naszym przypadku było ich tylko 2. Im więcej przyłączonych elementów tym większe wyjdą rozbieżności.

8. Ćwiczenie 6

• Dane z programu SCC

Zwarcie w węźle : URS212 Un = 220.00 kV; uziemiony punkt neutralny

NWE	NWP	Szw	3F	2F	1F	3I0	Z1	Z0	Z0/Z1
Jednostki		[MVA]	[A]	[A]	[A]	[A]	[Ω]	[Ω]	[-]
	URS212	1070	2808	2432	3175	3175	49,75	32,52	0,65
LIN12	BOR212	512	1344	1164	1170	473	103,92	218,42
URS-T1	URS512	558	1465	1268	2005	2705	95,39	38,17

• Obliczenia

3I0 = 2705A

I_1F = 2005A

I_OY =

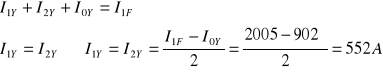
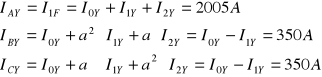
ZAŁOŻENIA: Transformator Yd11 ;
= 242kV/13,8kV = 17,5

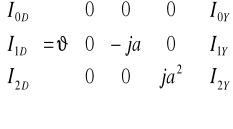
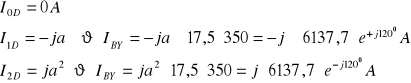
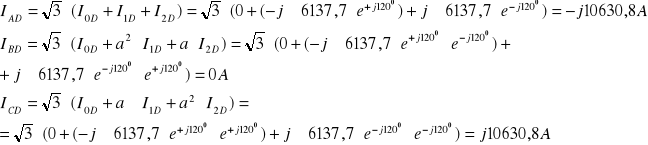
• Schemat poglądowy:

• Rozpływ otrzymany w programie SCC:

9. Ćwiczenie 7

• Dane z programu SCC

Zwarcie w węźle : URS212 Un = 220.00 kV; izolowany punkt neutralny

NWE	NWP	Szw	3F	2F	1F	3I0	Z1	Z0	Z0/Z1
Jednostki		[MVA]	[A]	[A]	[A]	[A]	[Ω]	[Ω]	[-]
	URS212	1070	2808	2432	1320	1320	49,75	218,37	4,39
LIN12	BOR212	512	1344	1164	861	1320	103,92	218,42
URS-T1	URS512	558	1465	1268	459	0	95,39	1000,0

• Obliczenia

3I0 = 0A

I_1F = 459A

I_OY = 0A

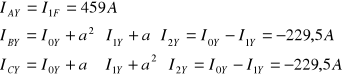
ZAŁOŻENIA: Transformator Yd11 ;
= 242kV/13,8kV = 17,5

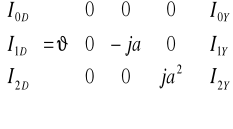
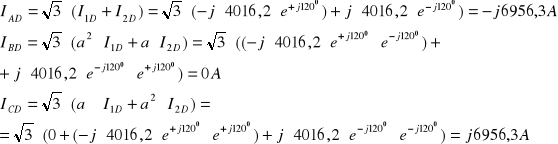
• Schemat poglądowy:

W układzie transformatora z izolowanym punktem neutralnym prąd płynący w fazie zwartej znacząco zmniejszył swoją wartość, natomiast prądy płynące w fazach zdrowych zmniejszyły się nieznacznie i zmieniły kierunek przepływu. Prądy płynące w uzwojeniu połączonym w trójkąt zmniejszyły swe wartości. W przypadku zwarcia doziemnego po stronie gwiazdy większe wartości prądów płynące od generatora mogą być dla niego niebezpieczne. Z tego powodu, a także dla tego, że 65% zwarć to zwarcia jednofazowe transformatory blokowe przy pomocy, których jest dołączony generator do systemu powinny pracować z uziemionym punktem neutralnym.

10. Ćwiczenie 8 i 9

• Dane z programu SCC

Miejsce zwarcia : linia LIN12 Un = 220.00 kV

NWE	NWP	Szw	3F	2F	1F	3I0	IW	Z2P	Z1P
Jednostki		[MVA]	[A]	[A]	[A]	[A]	[A]	[Ω]	[Ω]
W Ę Z Ł Y K R A Ń C O W E : BOR212 - URS212
	URS212	512	1344	1164	1170	473	350	59,8	60,0
	URS512	465	1220	1062	187	0	187	77,2	747,1
z tyłu	BOR212	-343	-901	-780	-833	-930	0	0,0	0,0
Jednostki		[MVA]	[A]	[A]	[A]	[A]	[A]	[Ω]	[Ω]
W Ę Z Ł Y K R A Ń C O W E : URS212 - BOR212
	BOR212	343	901	780	833	930	0	59,8	60,2
LIN12	ZAL212	122	319	276	214	182	0	342,8	403,0
URS-T1	KUL512	249	652	565	603	238	161	118,9	117,8
z tyłu	URS212	-512	-1344	-1164	-1170	-473	-350	0,0	0,0

Oznaczenia symboli:

S_zw - moc zwarciowa podana w MVA;

I_3F - prąd zwarcia trójfazowego podany w A;

I_2F - prąd zwarcia dwufazowego podany w A;

I_1F - prąd zwarcia jednofazowego podany w A;

3I0 - trzykrotna wartość prądu składowej zerowej podana w A;

I_W - prąd własny podany w A;

Z2P - impedancja zwarciowa dla zwarcia dwufazowego podana w Ω;

Z1P − impedancja zwarciowa dla zwarcia jednofazowego podana w Ω.

Węzły wybierane są na zasadzie wszystkich sąsiednich węzłów dla węzłów określających granice danej linii. W naszym przypadku „patrząc” z jednej strony linii L12 dla węzła BOR212 były to: URS212, ZAL212, KUL212. Natomiast z drugiej strony dla węzła URS212 były to węzły: URS512 i BOR212.

Wartości impedancji dla zwarć dwufazowego i jednofazowego są znaczne w porównaniu z wartościami w węzłach URS212 i BOR212.

Parametry linii.

Linia	R	X
−	Ω	Ω
LIN10	10,7	90,0
LIN11	3,5	30,8
LIN12	6,0	59,5

11. Ćwiczenie 10

W ćwiczeniu tym zgodnie z zaleceniami dodaliśmy 3 nowe zespoły wytwórcze, nową linię LIN30 łączącą węzły KUL212 - ZAL212 i system zastępczy w węźle ZAL212. Parametry poszczególnych modernizacji były zgodne z zaleceniami instrukcji.

Spośród zespołów wytwórczych zainstalowanych w węźle KUL212 co najmniej 2 transformatory blokowe muszą pracować z izolowanym punktem neutralnym ażeby był spełniony warunek :

Liczba transformatorów blokowych pracujących z uziemionym punktem neutralnym	0	1	2	3	4
X0/X1	7,8	1,7	0,9	0,7	0,5

Minimalny poziom wytrzymałości zwarciowej wyłączników zainstalowanych w stacjach KUL212 i ZAL212 dobierałem wg. następujących zależności:

I _dyn
i _p, I _zalN
i _p, I _Nw
I _b

Założenia: χ = 1,8; m = 0; n = 1; μ = 1

Tabela pomiarowa.

NWE	NWP	Szw	3F	2F	1F	3I0
Jednostki		[MVA]	[A]	[A]	[A]	[A]
ZWARCIE W WĘŹLE : KUL212 Un = 220kV
KUL2-02	Generator	1348	3537	3063	2400	0
KUL2-03	Generator	1348	3537	3063	2400	0
KUL2-04	Generator	1348	3537	3063	5351	8855
KUL-G1	Generator	1348	3537	3063	5351	8855
LIN11	BOR212	565	1483	1284	1255	750
LIN30	ZAL212	1169	3067	2656	2494	1238
LIN7	LAG211	450	1181	1023	975	522
Jednostki		[MVA]	[A]	[A]	[A]	[A]
ZWARCIE W WĘŹLE : ZAL212 Un = 220kV
LIN10	BOR212	370	970	840	690	438
LIN2	URZ211	543	1425	1234	1166	1101
LIN30	KUL212	1001	2628	2276	2026	1650
LIN6	LAG211	419	1099	952	808	575
ZAL2-01	Udział	14926	39169	33922	33482	34427

Wzory:

i _p = χ ·
· I _max

I _b = μ · I _max

I _th = I _max ·

Uzyskane wyniki:

Obiekt	i p	I b	I th	I dyn	I załN	I Nw
−	A	A	A	A	A	A
Zwarcie w węźle KUL212
KUL−G02	9168	3537	3537
KUL−G03	9178	3537	3537
KUL−G04	13870	5351	5351
KUL−G1	13870	5351	5351
LIN11	3844	1483	1483
LIN30	7950	3067	3067
LIN7	3061	1181	1181
Zwarcie w węźle ZAL212
LIN10	2514	970	970
LIN2	3694	1425	1425
LIN30	6812	2628	2628
LIN6	2849	1099	1099
ZAL2-01	101526	39169	39169

Określenie prądu doziemnego branego pod uwagę w przypadku zagrożenia porażeniowego w stacji KUL212.

Założenie: współczynniki redukcji linii k _r = 0,5.

12. WNIOSKI KOŃCOWE:

15

---