POLITECHNIKA RZESZOWSKA
im. Ignacego Łukasiewicza
KATEDRA INFORMATYKI I AUTOMATYKI
STEROWANIE WIELOWYMIAROWE
PROJEKT
Bartłomiej Haraszczuk
IV EDA L01
Rzeszów 2007
Treść zadania (Zad. 12.)
Na układ dwóch mas przedstawiony na rysunku działa siła, która powoduje przesunięcie.
Należy zaprojektować regulator metodą lokacji biegunów.
Dane:
x, y [m] - przesunięcie
m1, m2 [kg] - masa
F [N] - siła
k1 [Ns/m] - współczynnik tarcia lepkiego
k2 [N/m] - stała sprężyny
Dane liczbowe: m1 = 1, m2 = 2, k1 =0.2, k2 = 1
Równania dynamiki:
![]()
![]()
![]()
Przyjmując y jako wyjście oraz
![]()
, ![]()
, ![]()
, ![]()
, ![]()
, otrzymujemy

, 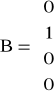
, ![]()
, ![]()
Rozwiązanie:
Zadanie zostało wykonane przy użyciu pakietu MATLAB/SIMULINK.
1. Wyznaczenie odpowiedzi skokowej układu otwartego
Macierze równania stanu
>>A=[0 1 0 0; -1 -0.2 1 0.2; 0 0 0 1; 0.5 0.1 -0.5 -0.1]
A =
0 1 0 0
-1 -0.2 1 0.2
0 0 0 1
0.5 0.1 -0.5 -0.1
>>B=[0;1;0;0]
B =
0
1
0
0
>>C=[0 0 1 0]
C =
0 0 1 0
>>D=[0]
D =
0
Transmitancja układu otwartego
>>[L,M]=ss2tf(A,B,C,D)
L =
0 3.8858e-016 6.6613e-016 0.1 0.5
M =
1 0.3 1.5 1.3617e-017 0
![]()
Zera i bieguny układu otwartego
>>[zo,po,k]=ss2zp(A,B,C,D,1)
zo =
-5.0000
po =
-0.1500 + 1.2155i
-0.1500 - 1.2155i
-0.0000
0
k =
0.1000
Uproszczenie par zer i biegunów
>>[Lm,Mm]=minreal(L,M)
0 pole-zero(s) cancelled
Lm =
0 3.8858e-016 6.6613e-016 0.1 0.5
Mm =
1 0.3 1.5 1.3617e-017 0
Odpowiedź skokowa układu otwartego
>>t=0:0.1:300
>>y=step(L,M,t)
>>plot(t,y);grid
Rys. 1.1. Odpowiedź skokowa układu otwartego
2. Sterowalność i obserwowalność modelu
Sterowalność pary (A,B)
>>Qs=ctrb(A,B)
Qs =
0 1 -0.2 -0.94
1 -0.2 -0.94 0.582
0 0 0.1 0.47
0 0.1 0.47 -0.291
>>RANK_Qs=rank(Qs)
RANK_Qs =
4
Obserwowalność pary (A,C)
>> Qo=obsv(A,C)
Qo =
0 0 1 0
0 0 0 1
0.5 0.1 -0.5 -0.1
-0.15 0.47 0.15 -0.47
>>RANK_Qo=rank(Qo)
RANK_Qo =
4
Korzystając z twierdzenia o sterowalności stwierdzam, iż model jest sterowalny, ponieważ rząd macierzy sterowalności Qs jest równy wymiarowi wektora stanu n.
W przykładzie para (AB) jest sterowalna, a więc układ (AB) jest sterowalny.Korzystając z twierdzenia o obserwowalności wnioskuje, iż model jest
obserwowalny, ponieważ rząd macierzy obserwowalności Qo jest równy
wymiarowi wektora stanu n.
3. Projektowanie liniowego regulatora stanu
Dobrze zaprojektowany układ sterowania powinien posiadać właściwości asymptotycznej stabilności, a ponadto przebiegi przejściowe powinny zanikać dostatecznie szybko i bez nadmiernych oscylacji.
W odniesieniu do systemów wysokiego rzędu (tak jak badanych układ), które nie dadzą się skutecznie aproksymować układami drugiego rzędu, można dokonać wyboru biegunów jak dla układów wzorcowych o transmitancji
![]()
Parametry transmitancji mogą być wyznaczone według kryterium minimum całki
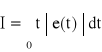
gdzie e(t) jest błędem w odpowiedzi na skok jednostkowy.
Powyższe kryterium określa się akronimem ITEA (Integral of Time multiplied by the Absolute value of Error).
Gdy nie jest pożądane przeregulowanie, proponuje się mianownik układu w formie wielomianu Bessela.
3.1. Wybór biegunów według ITAE
Dla badanego układu, który jest czwartego rzędu (n=4) dobieramy bieguny dodatkowo przemnożone przez współczynnik alfa. Następnie wyznaczymy odpowiedź skokową i impulsową dla dwóch wartości tego współczynnika pokazując w ten sposób jego wpływ na przeregulowanie pp i czas regulacji tr.
a) alfa=0.5
>>alfa=0.5;
>>p=alfa*[-0.424+1.263*i -0.424-1.263*i -0.626+0.4141*i
-0.626-0.4141*i];
>>K=place(A,B,p)
K =
-0.715 0.75 0.83999 -0.10001
>>Ac=A-B*K
Ac =
0 1 0 0
-0.285 -0.95 0.16 0.3
0 0 0 1
0.5 0.1 -0.5 -0.1
Transmitancja układu zamkniętego
>>[Lz,Mz]=ss2tf(Ac,B,C,D)
Lz =
0 -4.4409e-016 -1.5543e-015 0.1 0.5
Mz =
1 1.05 0.85 0.33749 0.062495
![]()
Uproszczenie par zer i biegunów
>> [Lz1,Mz1]=minreal(Lz(1,:),Mz)
0 pole-zero(s) cancelled
Lz1 =
0 -4.4409e-016 -1.5543e-015 0.1 0.5
Mz1 =
1 1.05 0.85 0.33749 0.062495
Odpowiedź skokowa układu zamkniętego
>>t1=0:0.1:40;
>> y1=step(Lz1,Mz1,t1);
>>plot(t1,y1);grid;
Rys. 3.1.1. Odpowiedź skokowa układu zamkniętego (alfa=0.5)
Przeregulowanie procentowe
>>pp = 100 * (max(y1) - y1(length(y1))) / y1(length(y1))
pp =
1.9548
Czas regulacji
>>trp = 0.1;
for i = 1:length(y1)
if abs((y1(i) - y1(length(y1))) / y1(length(y1))) * 100 > trp
tr = t1(i);
u=i;
end
end
>>tr
tr =
25.9
Odpowiedź impulsowa układu zamkniętego
>>t1=0:0.1:40;
>>u1=impulse(Lz,Mz,t1);
>>plot(t1,u1);grid
Rys. 3.1.2. Odpowiedź impulsowa układu zamkniętego (alfa=0.5)
Wyznaczanie macierzy korekcyjnej
>>L=[A B;C D]
L =
0 1 0 0 0
-1 -0.2 1 0.2 1
0 0 0 1 0
0.5 0.1 -0.5 -0.1 0
0 0 1 0 0
>>z=zeros(4,1)
z =
0
0
0
0
>>j=eye(1,1)
j =
1
>>P=[z;j]
p =
0
0
0
0
1
>>nn = L\P
nn =
1
0
1
0
0
>>Nx = nn(1:4, :)
Nx =
1
0
1
0
>>Nu = nn(5:5, :)
Nu =
0
>>N = Nu + K * Nx
N =
0.12499
Transmitancja układu zamkniętego z uwzględnieniem macierzy korekcyjnej
>>Ac=A-B*K;
Ac =
0 1 0 0
-0.285 -0.95 0.16 0.3
0 0 0 1
0.5 0.1 -0.5 -0.1
>>Bc=B*N
Bc =
0
0.12499
0
0
>>Cc=C-D*K
Cc =
0 0 1 0
>>Dc=D*N
Dc =
0
>>[Lc, Mc] = ss2tf(Ac, Bc, Cc, Dc)
Lc =
0 2.2204e-016 1.3323e-015 0.012499 0.062495
Mc =
1 1.05 0.85 0.33749 0.062495
![]()
>>[L1c, M1c] = minreal(Lc(1,:), Mc)
0 pole-zero(s) cancelled
L1c =
0 2.2204e-016 1.3323e-015 0.012499 0.062495
M1c =
1 1.05 0.85 0.33749 0.062495
Zera i bieguny układu zamkniętego z uwzględnieniem macierzy korekcyjnej
[zc pc] = ss2zp(Ac, Bc, Cc, Dc)
zc =
-5
pc =
-0.212 + 0.6315i
-0.212 - 0.6315i
-0.313 + 0.20705i
-0.313 - 0.20705i
Odpowiedz skokowa układu zamkniętego z uwzględniem macierzy korekcyjnej
>>t=0:0.01:30;
>>yy=step(L1c,M1c,t);
>>plot(t,yy),grid;
Rys. 3.1.3. Odpowiedź skokowa układu zamkniętego z uwzględnieniem N (alfa=0.5)
Przeregulowanie procentowe
>>pp = 100 * (max(y1) - y1(length(y1))) / y1(length(y1))
pp =
1.9069
Czas regulacji
>>trp = 0.1;
for i = 1:length(y1)
if abs((y1(i) - y1(length(y1))) / y1(length(y1))) * 100 > trp
tr = t1(i);
u=i;
end
end
>>tr
tr =
26.55
b) alfa=1
>>alfa=1;
>>p=alfa*[-0.424+1.263*i -0.424-1.263*i -0.626+0.4141*i
-0.626-0.4141*i];
>>K=place(A,B,p)
K =
1.4 1.8 0.59985 3.1999
>>Ac=A-B*K
Ac =
0 1 0 0
-2.4 -2 0.40 -2.99
0 0 0 1
0.5 0.1 -0.5 -0.1
Transmitancja układu zamkniętego
>>[Lz,Mz]=ss2tf(Ac,B,C,D)
Lz =
0 0 4.885e-015 0.1 0.5
Mz =
1 2.1 3.4 2.7 0.99992
![]()
Uproszczenie par zer i biegunów
>> [Lz1,Mz1]=minreal(Lz(1,:),Mz)
0 pole-zero(s) cancelled
Lz1 =
0 0 4.885e-015 0.1 0.5
Mz1 =
1 2.1 3.4 2.7 0.99992
Odpowiedź skokowa układu zamkniętego
>>t1=0:0.01:40;
>> y1=step(Lz1,Mz1,t1);
>>plot(t1,y1);grid;
Rys. 3.1.4. Odpowiedź skokowa układu zamkniętego (alfa=1)
Przeregulowanie procentowe
>>pp = 100 * (max(y1) - y1(length(y1))) / y1(length(y1))
pp =
2.1016
Czas regulacji
>>trp = 0.1;
for i = 1:length(y1)
if abs((y1(i) - y1(length(y1))) / y1(length(y1))) * 100 > trp
tr = t1(i);
u=i;
end
end
>>tr
tr =
12.8
Odpowiedź impulsowa układu zamkniętego
>>t1=0:0.1:40;
>>u1=impulse(Lz,Mz,t1);
>>plot(t1,u1);grid
Rys. 3.1.5. Odpowiedź impulsowa układu zamkniętego (alfa=1)
Wyznaczanie macierzy korekcyjnej
>>L=[A B;C D]
L =
0 1 0 0 0
-1 -0.2 1 0.2 1
0 0 0 1 0
0.5 0.1 -0.5 -0.1 0
0 0 1 0 0
>>z=zeros(4,1)
z =
0
0
0
0
>>j=eye(1,1)
j =
1
>>P=[z;j]
P =
0
0
0
0
1
>>nn = L\P
nn =
1
0
1
0
0
>>Nx = nn(1:4, :)
Nx =
1
0
1
0
>>Nu = nn(5:5, :)
Nu =
0
>>N = Nu + K * Nx
N =
1.9998
Transmitancja układu zamkniętego z uwzględnieniem macierzy korekcyjnej
>>Ac=A-B*K;
Ac =
0 1 0 0
-2.4 -2 0.4 -2.99
0 0 0 1
0.5 0.1 -0.5 -0.1
>>Bc=B*N
Bc =
0
1.9998
0
0
>>Cc=C-D*K
Cc =
0 0 1 0
>>Dc=D*N
Dc =
0
>>[Lc, Mc] = ss2tf(Ac, Bc, Cc, Dc)
Lc =
0 1.7764e-015 3.9968e-015 0.19998 0.99992
Mc =
1 2.1 3.4 2.7 0.99992
![]()
>>[L1c, M1c] = minreal(Lc(1,:), Mc)
0 pole-zero(s) cancelled
L1c =
0 1.7764e-015 3.9968e-015 0.19998 0.99992
M1c =
1 2.1 3.4 2.7 0.99992
Zera i bieguny układu zamkniętego z uwzględnieniem macierzy korekcyjnej
[zc pc] = ss2zp(Ac, Bc, Cc, Dc)
zc =
-5
pc =
-0.424 + 1.263i
-0.424 - 1.263i
-0.626 + 0.4141i
-0.626 - 0.4141i
Odpowiedz skokowa układu zamkniętego z uwzględniem macierzy korekcyjnej
>>t=0:0.01:30;
>>yy=step(L1c,M1c,t);
>>plot(t,yy),grid;
Rys. 3.1.6. Odpowiedź skokowa układu zamkniętego z uwzględnieniem N (alfa=1)
Przeregulowanie procentowe
>>pp = 100 * (max(y1) - y1(length(y1))) / y1(length(y1))
pp =
2.10
Czas regulacji
>>trp = 0.1;
for i = 1:length(y1)
if abs((y1(i) - y1(length(y1))) / y1(length(y1))) * 100 > trp
tr = t1(i);
u=i;
end
>>tr
tr =
12.8
3.2. Wybór biegunów filtru Bessela
Dla badanego układu, który jest czwartego rzędu (n=4) dobieramy bieguny dodatkowo przemnożone przez współczynnik beta. Następnie wyznaczymy odpowiedź skokową i impulsową dla dwóch wartości tego współczynnika pokazując w ten sposób jego wpływ na przeregulowanie pp i czas regulacji tr.
a) beta=0.5
beta=0.5;
p=beta*[-0.6573+0.8302*i -0.6573-0.8302*i -0.9047+0.2711*i -0.9047-0.2711*i]
K=place(A,B,p)
K =
-0.47956 1.262 0.60458 -0.48665
>>Ac=A-B*K
Ac =
0 1 0 0
-0.52 -1.462 0.39 0.68
0 0 0 1
0.5 0.1 -0.5 -0.1
Transmitancja układu zamkniętego
>>[Lz,Mz]=ss2tf(Ac,B,C,D)
Lz =
0 8.8818e-016 2.2204e-016 0.1 0.5
Mz =
1 1.562 1.098 0.40018 0.06251
![]()
Uproszczenie par zer i biegunów
>> [Lz1,Mz1]=minreal(Lz(1,:),Mz)
0 pole-zero(s) cancelled
Lz1 =
0 8.8818e-016 2.2204e-016 0.1 0.5
Mz1 =
1 1.562 1.098 0.40018 0.06251
Odpowiedź skokowa układu zamkniętego
>>t1=0:0.1:40;
>> y1=step(Lz1,Mz1,t1);
>>plot(t1,y1);grid;
Przeregulowanie procentowe
>>pp = 100 * (max(y1) - y1(length(y1))) / y1(length(y1))
pp =
0.83438
Czas regulacji
>>trp = 0.1;
for i = 1:length(y1)
if abs((y1(i) - y1(length(y1))) / y1(length(y1))) * 100 > trp
tr = t1(i);
u=i;
end
end
>>tr
tr =
17.03
Rys. 3.2.1. Odpowiedź skokowa układu zamkniętego (beta=0.5)
Odpowiedź impulsowa układu zamkniętego
>>t1=0:0.1:40;
>>u1=impulse(Lz,Mz,t1);
>>plot(t1,u1);grid
Rys. 3.2.2. Odpowiedź impulsowa układu zamkniętego (beta=0.5)
Wyznaczanie macierzy korekcyjnej
>>L=[A B;C D]
L =
0 1 0 0 0
-1 -0.2 1 0.2 1
0 0 0 1 0
0.5 0.1 -0.5 -0.1 0
0 0 1 0 0
>>z=zeros(4,1)
z =
0
0
0
0
>>j=eye(1,1)
j =
1
>>P=[z;j]
p =
0
0
0
0
1
>>nn = L\P
nn =
1
0
1
0
0
>>Nx = nn(1:4, :)
Nx =
1
0
1
0
>>Nu = nn(5:5, :)
Nu =
0
>>N = Nu + K * Nx
N =
0.12502
Transmitancja układu zamkniętego z uwzględnieniem macierzy korekcyjnej
>>Ac=A-B*K;
Ac =
0 1 0 0
-0.52 -1.462 0.395 0.68
0 0 0 1
0.5 0.1 -0.5 -0.1
>>Bc=B*N
Bc =
0
0.12502
0
0
>>Cc=C-D*K
Cc =
0 0 1 0
>>Dc=D*N
Dc =
0
>>[Lc, Mc] = ss2tf(Ac, Bc, Cc, Dc)
Lc =
0 -8.8818e-016 -8.8818e-016 0.012502 0.06251
Mc =
1 1.562 1.098 0.40018 0.06251
![]()
>>[L1c, M1c] = minreal(Lc(1,:), Mc)
0 pole-zero(s) cancelled
L1c =
0 -8.8818e-016 -8.8818e-016 0.012502 0.06251
M1c =
1 1.562 1.098 0.40018 0.06251
Zera i bieguny układu zamkniętego z uwzględnieniem macierzy korekcyjnej
[zc pc] = ss2zp(Ac, Bc, Cc, Dc)
zc =
-5
pc =
-0.32865 + 0.4151i
-0.32865 - 0.4151i
-0.45235 + 0.13555i
-0.45235 - 0.13555i
Odpowiedz skokowa układu zamkniętego z uwzględnieniem macierzy korekcyjnej
>>t=0:0.01:30;
>>yy=step(L1c,M1c,t);
>>plot(t,yy),grid;
Rys. 3.2.3. Odpowiedź skokowa układu zamkniętego z uwzględnieniem N (beta=0.5)
Przeregulowanie procentowe
>>pp = 100 * (max(y1) - y1(length(y1))) / y1(length(y1))
pp =
0.83438
Czas regulacji
>>trp = 0.1;
for i = 1:length(y1)
if abs((y1(i) - y1(length(y1))) / y1(length(y1))) * 100 > trp
tr = t1(i);
u=i;
end
end
>>tr
tr =
17.03
b) beta=1
beta=1;
p=beta*[-0.6573+0.8302*i -0.6573-0.8302*i -0.9047+0.2711*i -0.9047-0.2711*i]
K=place(A,B,p)
K =
2.2916 2.824 -0.29131 3.1788
>>Ac=A-B*K
Ac =
0 1 0 0
-3.2916 -3.024 1.2913 -2.9788
0 0 0 1
0.5 0.1 -0.5 -0.1
Transmitancja układu zamkniętego
>>[Lz,Mz]=ss2tf(Ac,B,C,D)
Lz =
0 -3.5527e-015 -4.4409e-015 0.1 0.5
Mz =
1 3.124 4.3919 3.2014 1.0002
![]()
Uproszczenie par zer i biegunów
>> [Lz1,Mz1]=minreal(Lz(1,:),Mz)
0 pole-zero(s) cancelled
Lz1 =
0 -3.5527e-015 -4.4409e-015 0.1 0.5
Mz1 =
1 3.124 4.3919 3.2014 1.0002
Odpowiedź skokowa układu zamkniętego
>>t1=0:0.1:40;
>> y1=step(Lz1,Mz1,t1);
>>plot(t1,y1);grid;
Rys. 3.2.4. Odpowiedź skokowa układu zamkniętego (beta=1)
Przeregulowanie procentowe
>>pp = 100 * (max(y1) - y1(length(y1))) / y1(length(y1))
pp =
0.87
Czas regulacji
>>trp = 0.1;
for i = 1:length(y1)
if abs((y1(i) - y1(length(y1))) / y1(length(y1))) * 100 > trp
tr = t1(i);
u=i;
end
>>tr
tr =
8.60
Odpowiedź impulsowa układu zamkniętego
>>u1=impulse(Lz,Mz,t1);
>>figure;
>>plot(t1,u1);grid
Rys. 3.2.5. Odpowiedź impulsowa układu zamkniętego (beta=1)
Wyznaczanie macierzy korekcyjnej
>>L=[A B;C D]
L =
0 1 0 0 0
-1 -0.2 1 0.2 1
0 0 0 1 0
0.5 0.1 -0.5 -0.1 0
0 0 1 0 0
>>z=zeros(4,1)
z =
0
0
0
0
>>j=eye(1,1)
j =
1
>>P=[z;j]
p =
0
0
0
0
1
>>nn = L\P
nn =
1
0
1
0
0
>>Nx = nn(1:4, :)
Nx =
1
0
1
0
>>Nu = nn(5:5, :)
Nu =
0
>>N = Nu + K * Nx
N =
2.0003
Transmitancja układu zamkniętego z uwzględnieniem macierzy korekcyjnej
>>Ac=A-B*K;
Ac =
0 1 0 0
-3.29 -3.024 1.29 -2.97
0 0 0 1
0.5 0.1 -0.5 -0.1
>>Bc=B*N
Bc =
0
2.0003
0
0
>>Cc=C-D*K
Cc =
0 0 1 0
>>Dc=D*N
Dc =
0
>>[Lc, Mc] = ss2tf(Ac, Bc, Cc, Dc)
Lc =
0 0 -7.1054e-015 0.20003 1.0002
Mc =
1 3.124 4.3919 3.2014 1.0002
![]()
>>[L1c, M1c] = minreal(Lc(1,:), Mc)
0 pole-zero(s) cancelled
L1c =
0 0 -7.1054e-015 0.20003 1.0002
M1c =
1 3.124 4.3919 3.2014 1.0002
Zera i bieguny układu zamkniętego z uwzględnieniem macierzy korekcyjnej
[zc pc] = ss2zp(Ac, Bc, Cc, Dc)
zc =
-5
pc =
-0.6573 + 0.8302i
-0.6573 - 0.8302i
-0.9047 + 0.2711i
-0.9047 - 0.2711i
Odpowiedz skokowa układu zamkniętego z uwzględniem macierzy korekcyjnej
>>t=0:0.01:30;
>>yy=step(L1c,M1c,t);
>>plot(t,yy),grid;
Rys. 3.2.6. Odpowiedź skokowa układu zamkniętego z uwzględnieniem N(beta=1)
Przeregulowanie procentowe
>>pp = 100 * (max(y1) - y1(length(y1))) / y1(length(y1))
pp =
0.86958
Czas regulacji
>>trp = 0.1;
for i = 1:length(y1)
if abs((y1(i) - y1(length(y1))) / y1(length(y1))) * 100 > trp
tr = t1(i);
u=i;
end
end
>>tr
tr =
8.43
4. Symulacja układu regulacji w SIMULINK-u.
Schemat układu regulacji
Rys. 4.1. Schemat badanego układu regulacji w SIMULINK-u
Parametry wpisane w poszczególnych bloczkach
Step
- step time: 0
- initial value: 0
- final value: 1
Stane-Space
Tutaj jako parametry wpisujemy macierze, które uprzednio zostały wprowadzone w linii poleceń MATLAB-a.
- A: A
- B: B
- C: eye[4,4]
- D: zeros[4,1]
Matrix Gain (K)
Parametrem jest wartość wzmocnienia K, wpisana w zależności od wyboru wartości parametrów alfa i beta.
- Gain matrix: K
Matrix Gain (C)
Parametrem jest macierz C.
- Gain matrix: C
Graph scope (u, y, wszystkie)
- time range 30
- y-min -2
- y-max 2
Gain (N)
- Gain: N
Saturation
- Lower output limit: -55
- Upper output limit: 55
Przebiegi
a) alfa=0.5
Rys. 4.2. Wymuszenie sterujące u(t) Rys. 4.3. Zmienna procesowa y(t)
b) alfa=1
Rys. 4.4. Wymuszenie sterujące u(t) Rys. 4.5. Zmienna procesowa y(t)
c) beta=0.5
Rys. 4.6. Wymuszenie sterujące u(t) Rys. 4.7. Zmienna procesowa y(t)
d) beta=1
Rys. 4.8. Wymuszenie sterujące u(t) Rys. 4.9. Zmienna procesowa y(t)
5. Wnioski
Jak wspomniano na początku, obiekt został przebadany w pakiecie MATLAB/SIMULINK. Bieguny zostały dobrane według kryterium ITAE oraz prototypowego filtru Bessela a następnie przemnożone przez współczynniki, odpowiednio alfa i beta. W obydwu przypadkach (ITAE, Bessel) przy wzroście współczynników maleje czas regulacji tr, kosztem spadku wzmocnienia k
i wzrostu przeregulowania p. Ma to swoje logiczne wytłumaczenie w momencie gdy postaramy się zobrazować sobie zachodzące zjawisko. Im większą siłą F (wzmocnienie) zadziałamy na badany obiekt tym szybciej spowodujemy jego przemieszczenie się (czas regulacji) przy jednoczesnym spadku stabilności przemieszczenia (przeregulowanie). W tym miejscu należy zaznaczyć, że przeregulowanie występuje tylko dla przebiegów oscylacyjnych, tłumionych „ITAE”, co oczywiście zgodne jest z założeniami teoretycznymi zamieszczonymi w literaturze,
o których możemy dowiedzieć się więcej choćby z pozycji [1]. Przebiegi otrzymane w trakcie symulacji układu SIMULINK-iem są prawie identyczne z wyznaczonymi w MATLAB-ie, co dodatkowo potwierdza poprawność wykonania doświadczenia.
Z powyższych rozważań wynika, że można tak dobrać bieguny, aby uzyskać określoną wartość przeregulowania (lub nawet jego brak) oraz czasu trwania regulacji, oczywiście
w racjonalnych granicach i zachowując pewien kompromis.
Na koniec chciałbym zaznaczyć, że obliczenia zostały wykonane w MATLAB-ie wersji 6.5, natomiast symulacja została przeprowadzona w SIMULINK-u wersji 4.0, ponieważ w wersji 6.5 SIMULINK-a przebiegi były generowane niewłaściwie i nie potrafiłem tego zniwelować.
6. Literatura
[1] Wysocki M., Sterowanie wielowymiarowe, Oficyna Wydawnicza PRz, Rzeszów 2004.
[2] Trybus L., Teoria sterowania, Oficyna Wydawnicza PRz, Rzeszów 2005.
[3] Kaczorek T., Teoria sterowania i systemów, PWN, Warszawa 1996.
[4] Brzózka J., Ćwiczenia z automatyki w MATLABIE i SIMULINKU, Mikon, Warszawa 1997.
Wysocki M., Sterowanie wielowymiarowe, Oficyna Wydawnicza PRz, Rzeszów 2004, str. 81
Wysocki M., Sterowanie wielowymiarowe, Oficyna Wydawnicza PRz, Rzeszów 2004, str. 94, 95
25
Wyszukiwarka