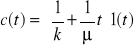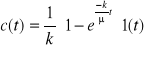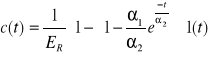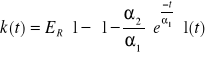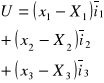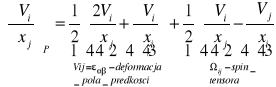RÓWNANIA NAVIERA STOCKESA (+ WARUNEK STOKES'A):
Dla płynów mamy równania:
a) rów. ciągłości: ![]()
b) rów. ruchu: ![]()
c) rów. konstytutywne Stokes'a: ![]()
warunek Stokes'a: ![]()
d) rów. energii:![]()
e) kinematyczne równanie stanu: p=p(ρ,T)
f) kaloryczne równanie stanu: ζ=ζ(ρ,T)
g) przewodność cieplna: ![]()
h) rów. przewodnictwa: ![]()
1) dla płynu ściśliwego:
![]()
2) dla płynu nieściśliwego: ![]()
Niewia |
σij |
Vi |
hi |
ρ |
T |
ξ |
Vij |
Liczba |
6 |
3 |
3 |
1 |
1 |
1 |
6 |
RÓWNANIA KONSTYTUTYWNE:
- łączą odkształcenia z naprężeniami dla liniowego zakresu ciała sprężystego
- wyrażają fizyczne (mech.) własności materiałowe
![]()
- liniowe ciało sprężyste stałe
![]()
- liniowy lepki płyn
Założenia:
- liniowa sprężystość - mała deformacja
Wtedy różnica pomiędzy opisem Lagrangea i Eulera jest pomijalna:
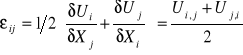
Uogólnione prawo Hooke'a ![]()
![]()
Tensor współczynników sprężystości Cijkm ma 34=81 współrzędnych. Symetryczność tensorów ![]()
i ![]()
pozwala zmniejszyć liczbę współrzędnych tensora ![]()
Zmiana zapisu na wygodniejszy:
![]()
; ![]()
; ![]()
; ![]()
![]()
; ![]()
analogicznie jest dla ![]()

Ciała izotropowe:
Tensor ![]()
musi być tensorem izotropowym czwartego rzędu. Każde odkształcenie ortogonalne tego tensora nie zmienia wartości jego współrzędnych. Można zapisać:
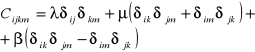
![]()
- skalary
z powodu symetrii mamy: ![]()
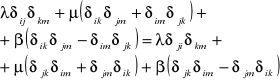
Po rozwiązaniu otrzymujemy: β = -β → β=0
![]()
; μ = G
otrzymujemy: ![]()
Wstawiamy własności delty Kronecker'a
![]()
Ciało izotropowe: ![]()
λ, μ - stałe Lamego

Zależność odwrotna, po przekształceniach matemat.:
![]()
Znana postać prawa Hooke'a
![]()
![]()
![]()
![]()
![]()
![]()
, gdzie:
E - moduł Younga ; ν - liczba Poissona
![]()
; ![]()
Moduł Kirchoffa: ![]()
; ![]()
Moduł sprężystości objętościowej: ![]()
Dla Ciała izotropowego i liniowo sprężystego główne kierunki naprężeń i odkształceń pokrywają się.

MODELE CIAŁ STAŁYCH:
Model Maxwela (lepko sprężysty):
|
F=k(u-u1) ;
|
Model Voighta (ciało stałe):
|
|
Standardowy model ciała (Kelwina):
|
α1, α2, ER - stałe materiałowe funkcje płynięcia
|
Funkcja płynięcia: Odpowiedz modeli na skokowy przyrost siły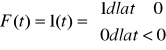
(odpowiedź przemieszczenie), siła jest skokiem jednostkowym
MAXWELL (pł) |
VOIGHT (pł) |
|
|
|
|
STANDARD (pł) |
STANDARD (RELAKSACJA) |
|
|
|
ER- relaksacyjny moduł sprężystości
|
Funkcja relaksacji: odpowiedź modeli na skokowy przyrost przemieszczenia (odpowiedzią jest siła), skok jednostkowy
MAXWELL (rel) |
VOIGHT (rel) |
|
|
|
|
PŁASKI STAN NAPRĘŻEŃ (dla ciał cienkich płaskich):
Założenia ![]()
Pozostają ![]()
![]()
i,j=1,2
1. równanie równowagi: ![]()
![]()
![]()
2. równanie deformacji: ![]()
![]()
![]()
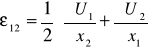
3. równania Hook'a (równ. wyjściowe):
![]()
![]()
![]()
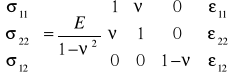
4. równanie zgodności
![]()
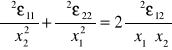
![]()
PŁASKI STAN DEFORMACJI (dla ciał cylindrycznych pryzmatycznych długich obciążonych poprzecznie):
X2 X1
X3 |
|
Założenia: ![]()
i ![]()
1. równ. równowagi: ![]()
2. równ. deformacji: ![]()
![]()
![]()
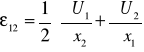
![]()
![]()
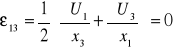
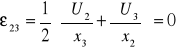
3. równ. Hooke'a:
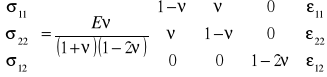
![]()
![]()
![]()
4. Podstawienia do równania równowagi (Navier'a-Stokes'a):
![]()
DEFORMACJA, ODKSZTAŁCENIA (Miary odkształceń):
|
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- tensor gradientu odkształceń ![]()
![]()
Zależności odwrotne:
![]()
![]()
Miary odkształcenia:
różnica kwadratów odległości punktów przed i po odkształceniu.
Zał. symbol Kronecker'a ![]()
![]()
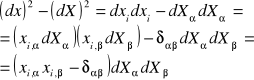
TENSORY:
a) tensor Greena:
![]()
![]()
![]()
Tensor odkszt. Greena: ![]()
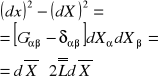
b) tensor Lagrange'a:
Tensor Lagrange'a odkszt. skończonych:![]()
![]()
Tensor odkszt. Lagrange'a: ![]()
![]()
- tensor jednostkowy zależności
zapis w Eulerze:
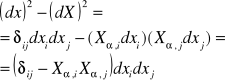
c) tensor Cauchy'ego:
![]()
![]()
![]()
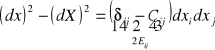
d) tensor odkształceń Eulera:
Tensor Eulera odkszt. skończonych: ![]()
![]()
- wszystkie tensory są symetryczne.
Linearyzacja:
Gdy odkształcenia są małe to można pominąć wielkości drugiego rzędu. Mamy do czynienia z tzw. infitezymalnym (nieskończenie małym) tensorem odkształceń: ![]()
![]()
; ![]()
; ![]()
Interpolacja geometryczna:
![]()
![]()
![]()
- współrzędna jednost wektora ![]()
w kierunku ![]()
![]()
po linearyzacji:
![]()
zakładamy że przemieszczenia są prostopadłe czyli ![]()
![]()
![]()
gdzie ![]()
-tensor Eulera
|
|
Odkształcenie liniowe jest niewielkie:
![]()
![]()
![]()
![]()
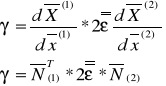
![]()
![]()
czyli:
![]()
![]()
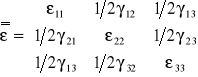
Odkształcenia płaskie:
1) wydłużenie w kierunku osi x1 x2
U1 dx2
dx1 x1 |
U2=0 |
2) skrócenie w kierunku osi x1 x2
U1 dx2 dx1 x1 |
|
3) czyste odkształcenie postaciowe x2
dx2
dx1 x1 |
|
x2 dx2
dx1 x1
|
brak odkształceń liniowych |
Pola prędkości:
dx
|
Rozkładamy gradient na część symetryczną i antysymetryczną: |
![]()
![]()
Składowa prędkości:
Wektor prędkości obrotowej ![]()
![]()
Gdy ![]()
znamy obrót z prędkością ![]()
jak ciała sztywnego
![]()
Równania zgodności:
Rozważamy płaski układ deformacji
![]()
![]()
![]()
![]()
![]()
dzielimy obustr. przez ![]()
![]()
dzielimy obustr. przez ![]()
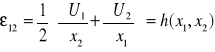
dzielimy obustr. przez ![]()
1) 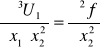
2) 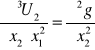
3) 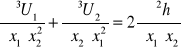
Warunki zgodności:
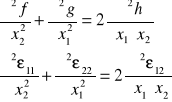
warunki dla płaskiego
Warunki równowagi dla ciała:
x1 |
|
Ciało o objętości V. Na element dV działają siły masowe ![]()
. Na element powierzchni ds. działają siły powierzchniowe ![]()
Pęd ciała w kierunku osi I: ![]()
, i=1, 2, 3
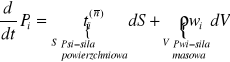
S - zamknięta powierzchnia ograniczająca
V - objętość
Z twierdzenia Gaussa:
![]()
przy czym: ![]()
![]()
Równanie ciągłości:
![]()
![]()
![]()
dla t=0, ![]()
, jeżeli m=const to ![]()
![]()
to ![]()
,
gdzie: ![]()
Jeżeli ciało nieściśliwe to w układzie materialnym w każdym punkcie ρ=const to ![]()
Pochodna materialna całki objętościowej:
![]()
→
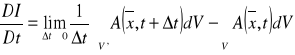
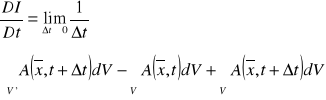
dla A=const ![]()
![]()
tw. Gaussa →
![]()
MES
Ciało o nieskończonej ilości punktów zamieniamy na skończoną liczbę Esów. Każdy element skończony zbudowany jest ze ścian, krawędzi i wierzchołków (więzów). Mamy skończoną liczbę elementów. Przemieszczenia nieskończonej ilości punktów uzależniamy od przemieszczeń skończonej liczby Esów które zależą od przemieszczeń swoich więzów.
![]()
- więzy mają swoja numerację
![]()
Procedura MES:
a) wybór równania przemieszczeń w celu wyznaczenia macierzy K,M
b) rozwiązanie układu równań liniowych - otrzymanie przemieszczenia węzłów
c) obliczenia deformacji i naprężeń
Zad.1
Wyznaczyć:
trajektorię cząstki X (1,2,1)
prędkość i przyspieszenie tej cząstki dla t=2s
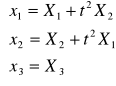
ad. A)
X (1,2,1)
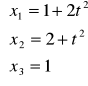
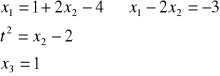
ad. B)
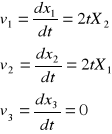
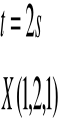
![]()
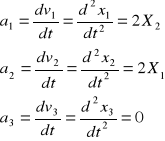
![]()
Zad. 2.
Odwrócić równania ruchu i obliczyć współrzędne prędkości i przyspieszenia dla ![]()
i t=2s
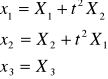
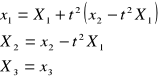
![]()
![]()
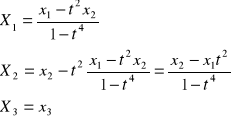
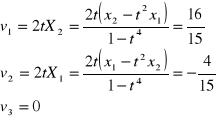
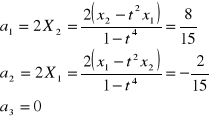
Zad. 3
Dany jest ruch w opisie Lagrenge'a. Przejść do Eulera.
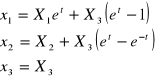
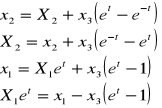
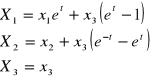
Zad. 4
Obliczyć prędk. i przyspiesz zadania 3 w zapisie Eulera.
Lagrange:
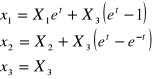
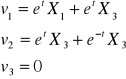
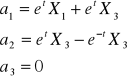
|
Eulera |
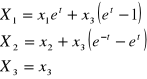
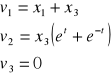
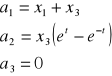
Zad. 5
Określ pole prędkości w układzie Eulera i pochodną substancjalną temperatury
![]()
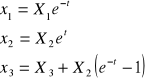
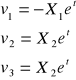
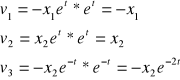
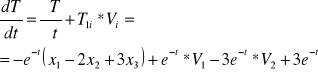
Wyszukiwarka