PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA

W PILE

SPRAWOZDANIE Z LABORATORIUM

Ćwiczenie nr 5 : Wyznaczenie siatki dyfrakcyjnej.

Data wykonania:

Wykonali:

1.Wstęp

Dyfrakcja

Zjawisko dyfrakcji (ugięcia) odkrył Grimaldi (XVII w). Polega ono na uginaniu się promieni świetlnych przechodzących w pobliżu przeszkody (np. brzeg szczeliny).

Wyjaśnienie dyfrakcji w oparciu o zasadę Huyghensa - Fresnel (przełom XVIII i XIX w). (W jego czasach wierzono, że fale świetlne są falami mechanicznymi w przenikającym wszechświat eterze. Dopiero Maxwell pokazał, że fale świetlne są falami elektromagnetycznymi, a Einstein odrzucił postulat konieczności istnienia eteru).

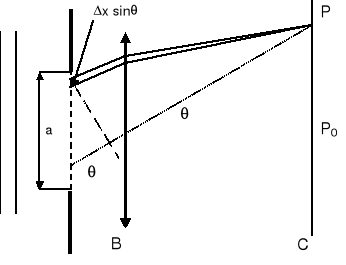
Rysunek (a) pokazuje ogólnie na czym polega dyfrakcja.

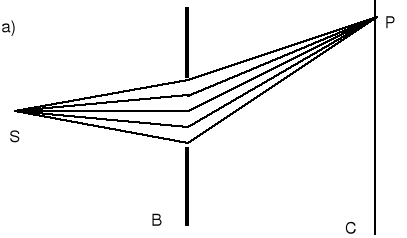
Fala ze źródła S pada na szczelinę B i przechodzące przez otwór pada na ekran C. Natężenie w punkcie P można obliczyć dodając do siebie wszystkie zaburzenia falowe (tj. wektory E). Te zaburzenia falowe mają różne amplitudy i fazy ponieważ:

• elementarne źródła Huyghensa (punkty w szczelinie) są w różnych odległościach od punktu P.

• światło opuszcza te punkty pod różnymi kątami.

Taka sytuacja gdy fale opuszczające otwór nie są płaskie (promienie nie są równoległe) pojawia się gdy źródło fal S i ekran (C), na którym powstaje obraz znajdują się w skończonej odległości od ekranu ze szczeliną (B). Taki przypadek nosi nazwę dyfrakcji Fresnela. Obliczenia natężeń światła są w tej sytuacji trudne.

Całość upraszcza się, gdy źródło S i ekran C odsuniemy na bardzo duże odległości od otworu uginającego. Ten graniczny przypadek nazywamy dyfrakcją Fraunhofera. Czoła fal padających jak i ugiętych są płaszczyznami (promienie są równoległe) tak jak to widać na rysunku (b).

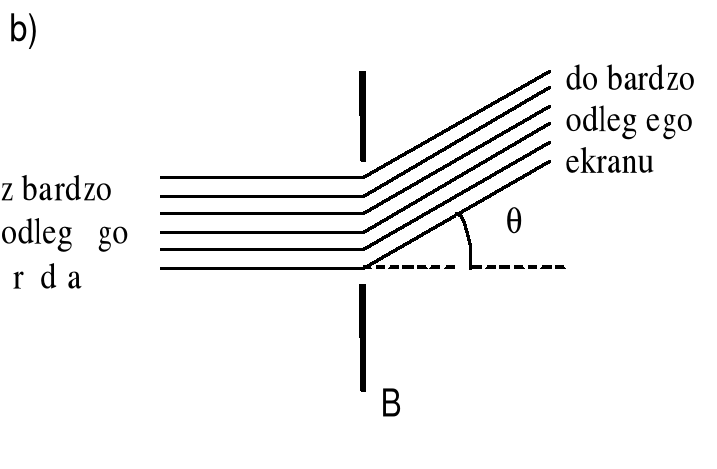
Warunki do wystąpienia dyfrakcji Fraunhofera można zrealizować w laboratorium za pomocą dwu soczewek (rysunek c).

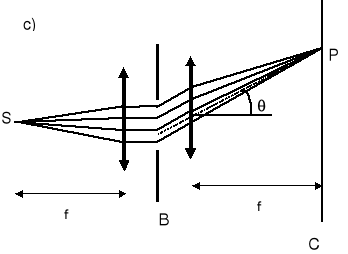
Pierwsza soczewka zmienia falę rozbieżną w równoległa, a druga skupia w punkcie P fale płaskie opuszczające otwór. Wszystkie promienie oświetlające punkt P opuszczają otwór równolegle do linii przerywanej (przechodzącej przez środek soczewki). Warunki dyfrakcji Fraunhofera były z założenia spełnione w doświadczeniu Younga.

Będziemy zajmować się tylko dyfrakcją Fraunhofera.

Pojedyncza szczelina

Rysunek pokazuje falę płaską padającą prostopadle na szczelinę o szerokości a. Interesuje nas punkt środkowy P₀ . Równoległe promienie przebywają do tego punktu te same drogi optyczne (różne geometryczne) tzn. promienie zawierają tę samą ilość długości fal (soczewki cienkie). Ponieważ w szczelinie promienie są zgodne w fazie to po przebyciu takich samych dróg optycznych nadal pozostają zgodne w fazie. Dlatego w środkowym punkcie P₀ będzie maksimum.

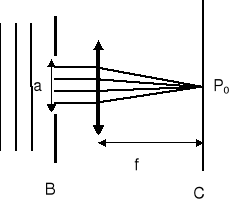
W innym przypadku (punkt P₁) promienie docierające do P₁ wychodzą ze szczeliny pod kątem θ. Jeden promień ma początek u góry szczeliny, a drugi w jej środku. (Promień xP₁ przechodzi przez środek soczewki więc nie jest odchylany).

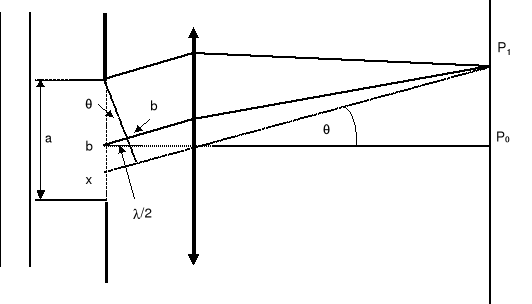
Jeżeli wybierzemy punkt P₁ tak, żeby różnica dróg bb' wynosiła λ/2 to promienie zgodne w fazie w szczelinie będą miały w punkcie P₁ fazy przeciwne i wygaszą się. Podobnie każdy inny promień wychodzący z górnej połowy szczeliny będzie się wygaszał z odpowiednim promieniem z dolnej połówki leżącym w odległości a/2 poniżej. Punkt P₁ będzie miał natężenie zerowe (pierwsze minimum dyfrakcyjne).

Warunek opisujący to minimum ma następującą postać

czyli

asinθ = λ

Uwaga: Gdyby szerokość szczeliny była równa λ wtedy pierwsze minimum pojawiłoby się dla θ = 90° czyli środkowe maksimum wypełniłoby cały ekran. W miarę rozszerzania szczeliny środkowe maksimum staje się węższe. (Podobnie było dla interferencji Younga w miarę zmiany odległości między szczelinami punktowymi). Podobne rozważania możemy powtórzyć dla wielu punktów szczeliny i otrzymamy ogólne wyrażenie dla minimów obrazu dyfrakcyjnego w postaci

asinθ = mλ, m = 1, 2, 3,...... (min.)

Mniej więcej w połowie między każdą parą sąsiednich minimów występują oczywiście maksima natężenia.

Pojedyncza szczelina, rozważania jakościowe

Wyrażenie na rozkład natężenia w całym obszarze dyfrakcyjnym w funkcji kąta θ. Wyobraźmy sobie, że szczelinę o szerokości a dzielimy na N pasków o małej szerokości Δx. Każdy pasek jest źródłem fal kulistych Huyghensa, które wytwarzają na ekranie określone zaburzenie falowe.

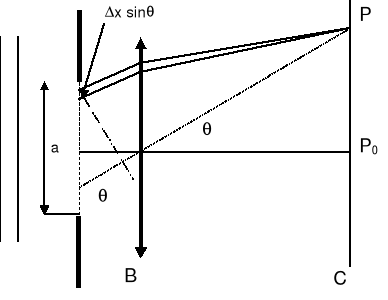
Różnica dróg między sąsiednimi paskami wynosi Δxsinθ stąd różnica faz Δϕ pomiędzy falami pochodzącymi z sąsiednich pasków wynosi

czyli

• Zakładamy, że paski są tak wąskie, że wszystkie punkty na danym pasku mają tę samą drogę optyczną do punktu P (całe światło ma tę samą fazę).

• Dla małych kątów θ amplitudy ΔE₀ zaburzeń falowych w punkcie P pochodzące od różnych pasków przyjmujemy za jednakowe.

Zatem w punkcie P dodaje się N wektorów (pól elektrycznych E) o tej samej amplitudzie ΔE₀, tej samej częstości i tej samej różnicy faz Δϕ między kolejnymi wektorami.

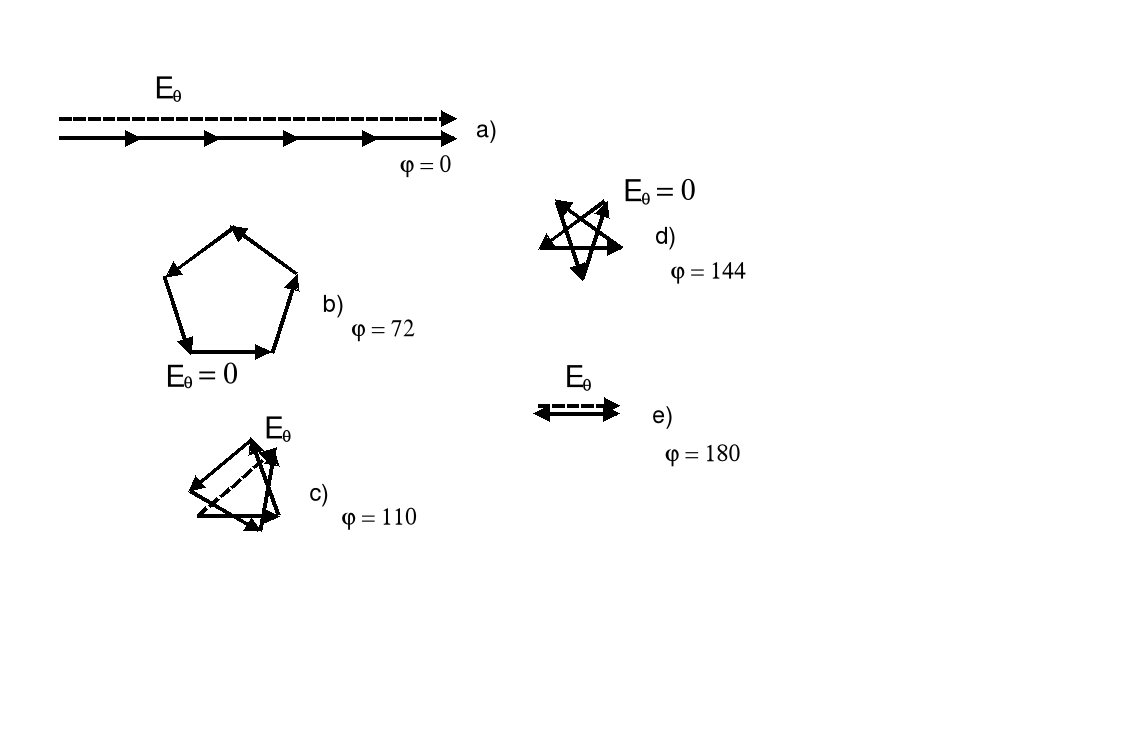
Zaburzenie wypadkowe dla różnych punktów P, tzn. dla różnych kątów θ, tzn. dla różnych Δϕ.Poniżej na rysunkach przedstawione jest zaburzenie wypadkowe dla kilku różnych miejsc na ekranie.

• Rysunek (a) przedstawia warunki dla maksimum środkowego (Δϕ=0°).

• Rysunek (b) przedstawia warunki dla kierunku nieco odmiennego od maksimum środkowego (Δϕ=5°).

• Rysunek (c) przedstawia warunki dla pierwszego minimum (Δϕ=30°).

• Rysunek (d) przedstawia warunki bliskie pierwszemu maksimum (poza środkowym) (Δϕ=42°).

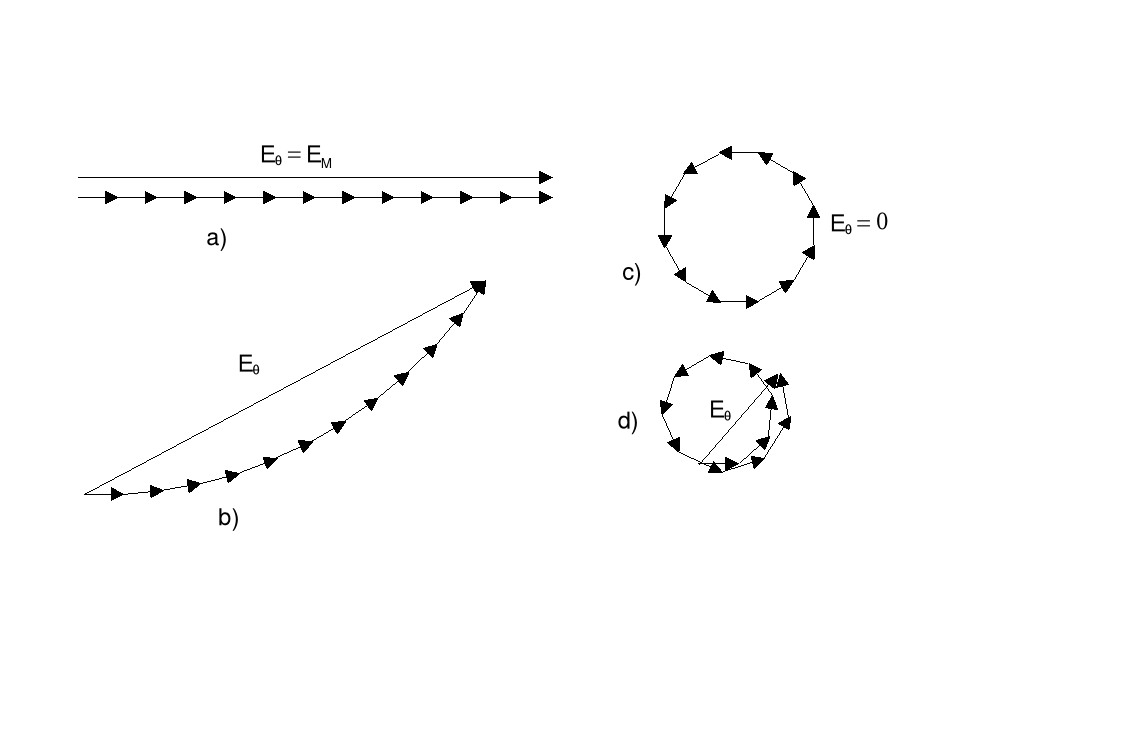
Zwróćmy uwagę, że długość łuku jest zawsze równa E_M ale amplituda E_θ jest różna. Wektory na rysunku odpowiadają amplitudom (a nie natężeniom). Żeby otrzymać natężenia trzeba je podnieść do kwadratu. W przeciwieństwie do obrazu interferencyjnego natężenia kolejnych maksimów nie są jednakowe.

Pojedyncza szczelina, rozważania ilościowe

Na rysunku poniżej jest przedstawiona konstrukcja służąca do obliczenia natężenia światła w przypadku dyfrakcji na jednej szczelinie. Sytuacja odpowiada tej pokazanej na poprzednim rysunku (b).

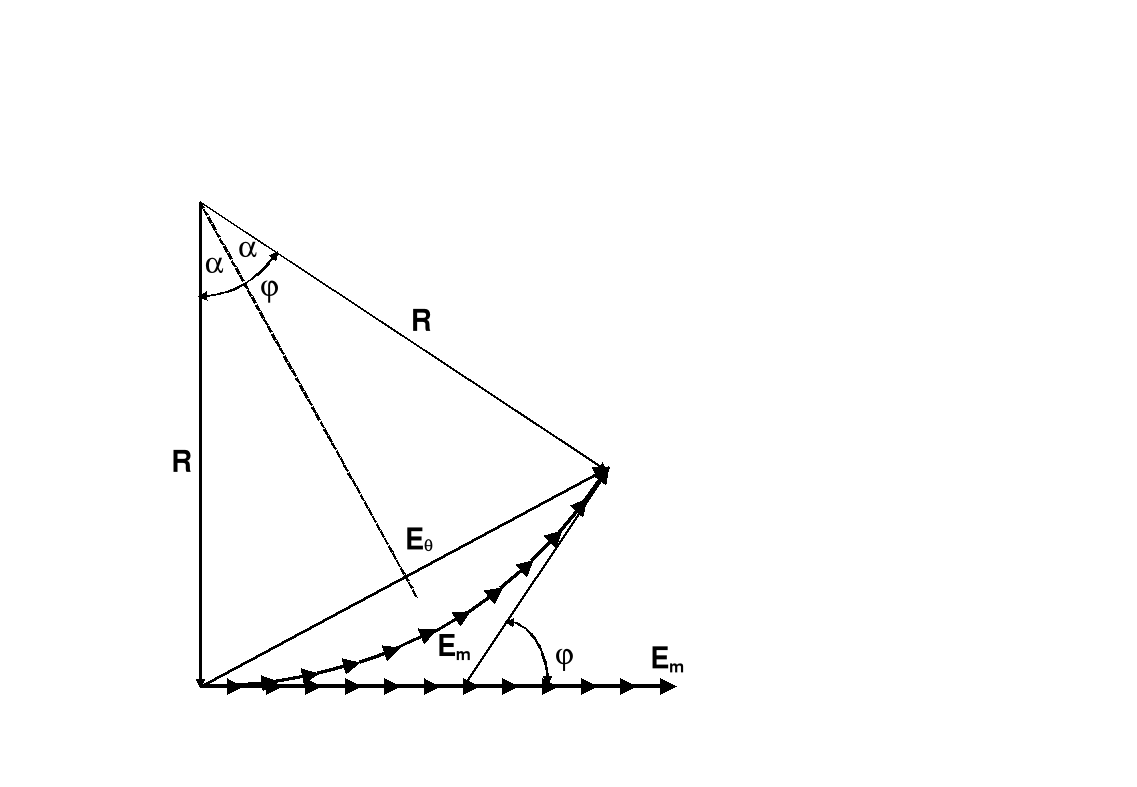
Jeżeli szczelinę podzielimy na nieskończenie wiele małych pasków o szerokości dx to łuk strzałek będzie łukiem koła o promieniu R. Długość łuku wynosi E_m czyli równa jest amplitudzie w środku obrazu dyfrakcyjnego (linia prosta strzałek).

Kąt ϕ w dolnej części rysunku przedstawia różnicę fazy między skrajnymi wektorami w łuku tzn. ϕ jest różnicą faz pomiędzy promieniami wychodzącymi z góry i dołu szczeliny.

Jak widać z rysunku

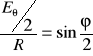
czyli

W mierze łukowej

Stąd

Podstawiając do równania otrzymamy

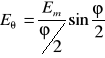
czyli

gdzie α = ϕ/2.

Przypomnijmy, że ϕ jest różnicą faz dla promieni wychodzących z krańców szczeliny.

Ponieważ różnica dróg dla tych promieni wynosi asinθ (a szerokość szczeliny) więc możemy posłużyć się znanym związkiem

różnica faz = różnica dróg 

otrzymując

lub

Teraz możemy już obliczyć natężenie światła dla dyfrakcji na pojedynczej szczelinie. Natężenie jest proporcjonalne do kwadratu amplitudy. Otrzymujemy więc

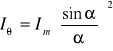
Wyrażenie na natężenie przyjmuje wartość minimalną dla

α = mπ, m = 1, 2, 3,....

Podstawiając do równania otrzymujemy

asinθ = mλ, m = 1, 2, 3, ..... (minimum)

Jest to wynik zgodny z uzyskanym poprzednio (rozważania jakościowe).

Obliczmy teraz względne natężenia kolejnych maksimów dyfrakcyjnych.

Maksima leżą w środku pomiędzy minimami, a więc w punktach, dla których

α = (m+1/2)π, m = 1, 2, 3,.......

Podstawiając to do równania na natężenie otrzymujemy

I_θ/I_m = 0.045, 0.016, 0.008 dla m = 1, 2, 3. Widać, że natężenia kolejnych maksimów bardzo szybko maleją.

Na rysunku poniżej przedstawiono krzywe I_θ dla różnych szerokości szczeliny (w stosunku do długości fali λ) w funkcji położenia na ekranie (kąta θ).

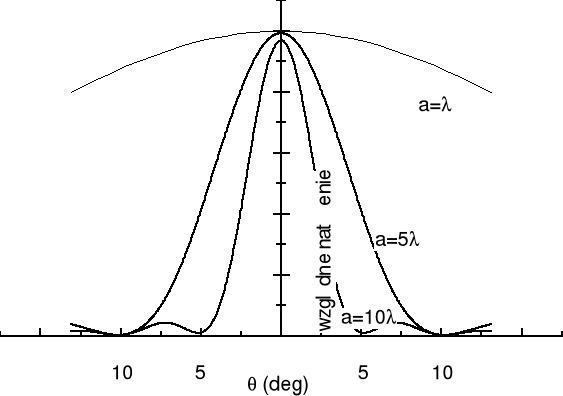
Równoczesna interferencja i dyfrakcja na dwóch szczelinach

W doświadczeniu Younga szczeliny były wąskie ( a << λ) tak, że każda ze szczelin oświetlała równomiernie ekran. Jeżeli takie fale (spójne) interferowały to otrzymywaliśmy prążki o jednakowym natężeniu.

Dla realnych szczelin trudno jest zrealizować warunek a << λ. Oznacza to, że pojedyncza szczelina będzie dawała obraz dyfrakcyjny i interferencja fal da teraz obraz, w którym natężenia prążków nie będą stałe (jak w doświadczeniu Younga) ale zależne od tego obrazu dyfrakcyjnego.

Odejście od założenia a << λ powoduje głównie zmianę natężenia prążków (ich położenia pozostają prawie nie zmienione).

Przypomnijmy, że obraz interferencyjny dla dwóch szczelin dany jest równaniem

gdzie

przy czym d jest odległością między szczelinami.

Natomiast natężenie fali ugiętej na szczelinie jest dane równaniem

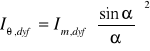
gdzie

przy czym a jest szerokością szczeliny.

Dlatego w równaniu dla interferencji stałą amplitudę (dla wąskich szczelin) zastępujemy realnym natężeniem dyfrakcyjnym. Otrzymujemy

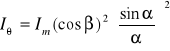
Ten wynik opisuje następujące fakty. W pewnym punkcie ekranu natężenie światła, z każdej szczeliny osobno, jest dane przez obraz dyfrakcyjny tej szczeliny.

Obrazy dyfrakcyjne dwóch szczelin rozpatrywanych oddzielnie nakładają się (fale interferują). Rysunek poniżej jest wykresem powyższego równania dla d = 50λ i trzech wartości stosunku a/λ.

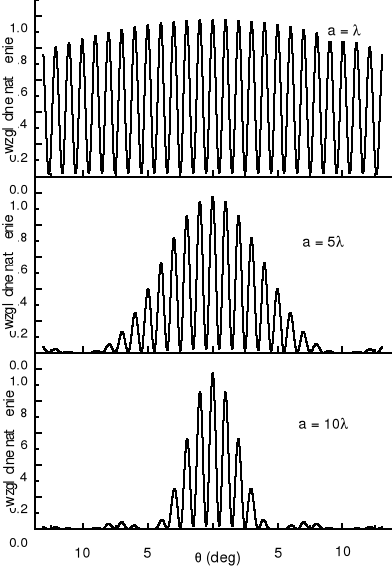
Obwiednie prążków interferencyjnych pokrywają się dokładnie z obrazem dyfrakcyjnym. Obraz jest więc iloczynem czynnika interferencyjnego i dyfrakcyjnego.

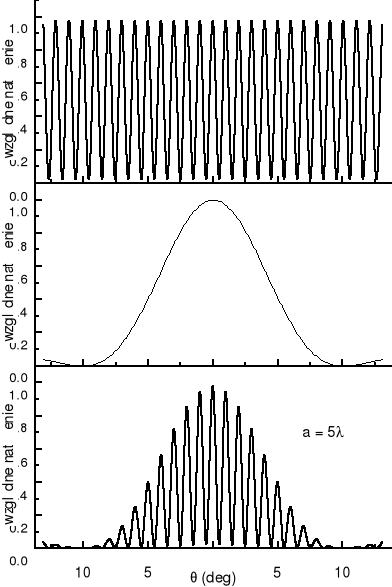
Czynnik interferencyjny (cos²β) jest pokazany na górnym wykresie, czynnik dyfrakcyjny (sinα/α)² na środkowym, a ich iloczyn na dolnym.

Siatki dyfrakcyjne

Układ zawierający zespół N równoległych szczelin nazywamy siatką dyfrakcyjną (szczelin może być b. dużo np. 10⁴/cm).

Na rysunku poniżej pokazany jest rozkład natężeń dla N = 5 szczelin.

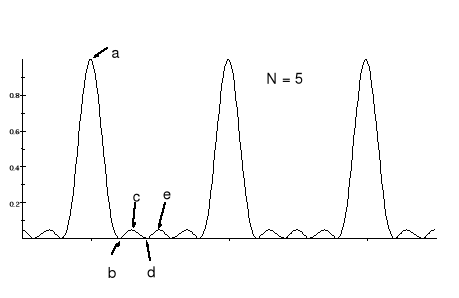
Z rysunku widać, że zwiększenie liczby szczelin

• nie zmienia odległości pomiędzy głównymi maksimami (przy stałych d i λ)

• nastąpiło natomiast ich zwężenie (wyostrzenie)

• pojawiły się wtórne maksima pomiędzy maksimami bocznymi

Maksima główne wystąpią gdy spełniony jest znany warunek

dsinθ = mλ, m = 0, 1, 2, (maks.)

gdzie m nazywamy rzędem widma, a d jest odległością między szczelinami (stała siatki dyfrakcyjnej).

Uwaga: Położenia maksimów głównych nie zależą od N.

Pochodzenia maksimów wtórnych można wyjaśnić za pomocą metody strzałek fazowych (wskazów).

Siatki dyfrakcyjne są często stosowane do pomiarów długości fali i do badań struktury i natężenia linii widmowych.

• Ponieważ stałą siatki dyfrakcyjnej można zmierzyć dokładnie pod mikroskopem to z warunku na występowanie głównych maksimów możemy wyznaczyć λ.

• Z tego samego warunku widać, że fale o różnych λ uginają się pod różnymi kątami jest więc szansa na ich rozseparowanie.

Dyspersją kątową siatki dyfrakcyjnej nazywamy wielkość
która informuje o odległości kątowej (rozdzieleniu) dwóch fal o mało różniących się długościach.

Natężenia linii siatki dyfrakcyjnej zależą od geometrii pojedynczej szczeliny. W idealnym przypadku zależą od szerokości szczeliny.

Tak samo natężenia wiązek rozproszonych na krysztale zależą od geometrii pojedynczej rozpraszającej komórki elementarnej.

2.Przebieg badania:

1. Przyrządy: -laser półprzewodnikowy (630-680 nm)

-siatka dyfrakcyjna

-miara

-ekran

2. Badanie:

Umieszczamy siatkę w pewnej odległości od ekranu,

uruchamiamy laser i mierzymy odległość między kolejnymi prążkami dyfrakcyjnymi (tzn. między prążkiem środkowym a kolejnymi). Pomiar wykonujemy

dla trzech różnych odległości.

3.Wzory :

1. długość fali

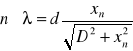
d - stała siatki

D - odległość ekranu

- odległość między prążkami

2. błąd statystyczny

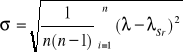
n - ilość pomiarów

- długość fali

3. błąd względny

- wartość średnia dł. fali podanej przez producenta

4. Zestawienie wyników pomiarów :

ODLEGŁOŚĆ OD EKRANU (m)	NUMER KOLEJNY PRĄŻKA	ODLEGŁOŚĆ MIĘDZY PRĄŻKAMI (m)	DŁUGOŚĆ FALI (nm)
1	1	0,064	639			-12	144
		2	0,129	640			-11	121
		3	0,198	647			-4	16
		4	0,268	647			-4	16
	1,3	1	0,085	652			1	1
		2	0,172	656			5	25
		3	0,258	649			-2	4
		4	0,352	654			3	9
	1,5	1	0,099	659			8	64
		2	0,199	658			7	49
		3	0,301	656			5	25
		4	0,403	649			-2	4

5. Obliczenie błędów :

1. błąd statystyczny

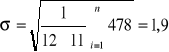
2. błąd względny

3. wartość długości fali

6. Wnioski :

Wartość długości fali nawet bez uwzględnienia błędów

pomiarowych i mimo nieprecyzyjnego przyrządu

mierniczego jakim jest metrówka mieszczą się w zakresie

podanym na obudowie lasera (630-680 nm). Pole tolerancji

o wielkości 0,000000050 m jest tak małe ,że praktycznie

trudno jest je sobie wyobrazić i zmieszczenie się z

prawidłowym wynikiem wykonując pomiary metrówką

i przy braku zaciemnienia można uznać za sukces.

Błąd 0,6 % o dużej dokładności wyniku.

Poniższy rysunek ilustruje graficznie nasz wynik :

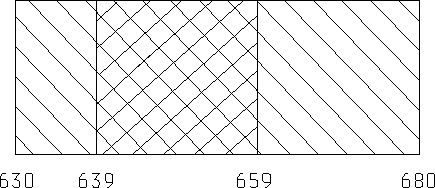
Podsumowując przebieg badania uważamy za udany

a uzyskane wyniki za zgodne z rzeczywistością.

1

---