![]()
Politechnika Lubelska
Laboratorium elektrotechniki
![]()
Temat ćwiczenia:
Obwody z elementami RLC.
Lublin 3 kwietnia 2002
Wykonał:
Łukasz Bąk
Piotr Biernacki
Piotr Chmiel
Jacek Dębowczyk
Grupa ED 2.6
Ocena :
....................
POLITECHNIKA LUBELSKA W LUBLINIE |
Laboratorium elektrotechniki |
||
|
Ćwiczenie nr 6 |
||
Nazwisko i Imię: Łukasz Bąk Piotr Biernacki Piotr Chmiel Jacek Dębowczyk |
Semestr:
II |
Grupa:
ED 2.6 |
Rok akademicki:
2001/2002 |
Temat ćwiczenia: Obwody z elementami RLC. |
Daty wykonania: 3 kwietnia 2002 |
Ocena: |
|
Cel ćwiczenia
Celem ćwiczenia jest doświadczalne potwierdzenie słuszności praw Kirchhoffa oraz sprawdzenie innych podstawowych zależności obowiązujących w obwodach prądu sinusoidalnie zmiennego.
Przyrządy pomiarowe:
autotransformator laboratoryjny EP43.3/1450
amperomierz elektromagnetyczny EP43.3/754
amperomierz elektromagnetyczny EP43.3/257
amperomierz elektromagnetyczny EP43.3/1638
amperomierz elektromagnetyczny E2/P3/80
amperomierz elektromagnetyczny EP43.3/1640
watomierz EP43.3/1761
woltomierz elektromagnetyczny 2212024/74
woltomierz elektromagnetyczny EP43.3./1761
woltomierz elektromagnetyczny EP43.3/327
rezystor suwakowy 60Ω; 0,63A; EP43.3/1565
rezystor suwakowy 46 Ω; 1,25A; EP43.3/1559
kondensator 10μF; EP1.436/179
kondensator 18μF;
cewka 0,628H; 121,5Ω
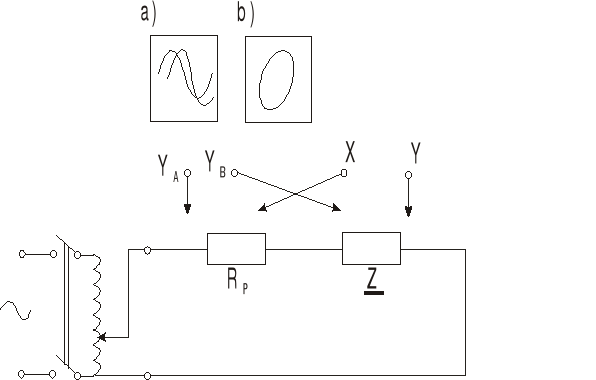
Wyznaczanie kąta fazowego impedancji:
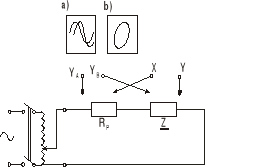
Rys 1. Schemat układu do wyznaczania kąta fazowego impedancji
kąt fazowy na oscyloskopie dwustrumieniowym wyznacza się na podstawie obserwacji wzajemnego przesunięcia przebiegu napięcia i prądu.
Rp=1,9 Ω 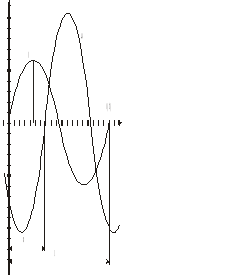
x = 1,3
l=3,8
![]()
![]()
![]()
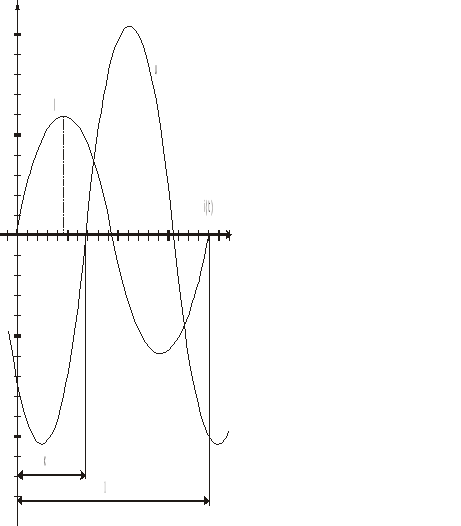
Rys. 2. Obraz z oscyloskopu dwustrumieniowego
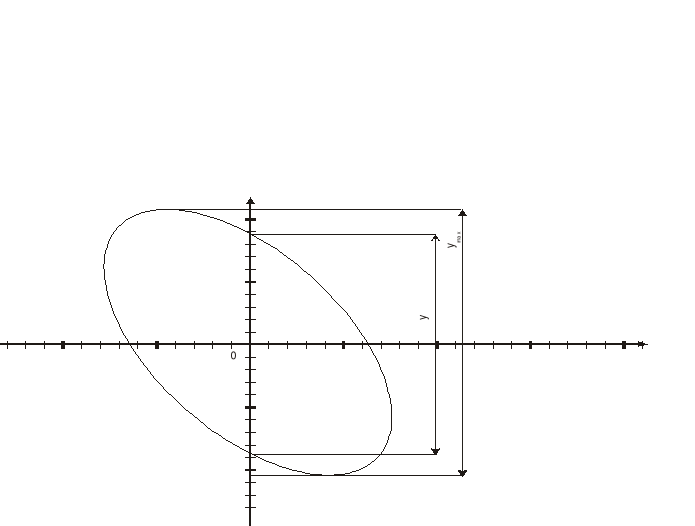
kąt fazowy na oscyloskopie z odchylaniem poziomym i pionowym wyznacza się na podstawie obrazu otrzymanego na jego ekranie
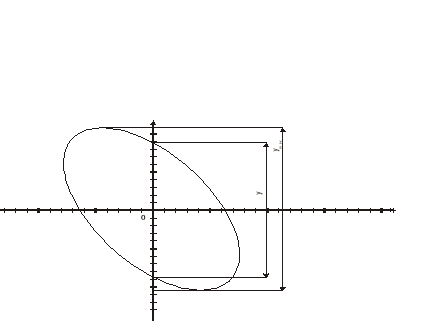
![]()
y = 3,8
![]()
ymax=4,4
![]()
![]()
![]()
Rys. 3. Obraz z oscyloskopu o odchyleniu pionowym i poziomym
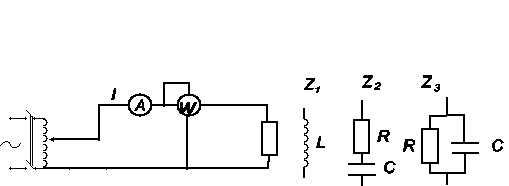
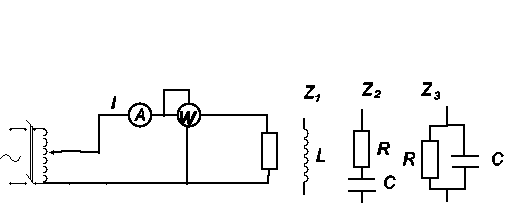
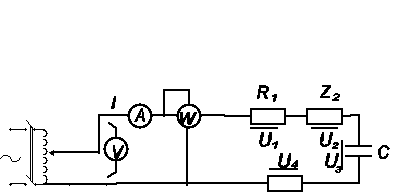
Wyznaczanie parametrów impedancji zastępczej:
impedancja ![]()
- cewka rzeczywista
![]()
- opornik i kondensator połączone szeregowo
![]()
- opornik i kondensator połączone równolegle
Rys. 4. Schemat pomiarowy układu do wyznaczania parametrów impedancji zastępczej (impedancje Z1 stanowi cewka rzeczywista).
Z |
Lp. |
Pomiary |
Obliczenia |
|||||||
|
|
U |
I |
φ |
cosφ |
Z |
R |
X |
P |
|
|
|
V |
A |
° |
--- |
Ω |
Ω |
Ω |
W |
|
Z1 |
1 |
58 118 182 |
0,25 0,50 0,75 |
59 62 58 |
0,517 0,458 0,527 |
232 236 243 |
119 124 128 |
199 208 206 |
7,5 33 72 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Średnie |
60 |
0,501 |
237 |
124 |
204 |
||||
Z2 |
1 |
10 21 32 |
0,25 0,50 0,75 |
-37 -18 0 |
0,800 0,952 1 |
40 42 43 |
32 40 43 |
24 13 0 |
2 10 24 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Średnie |
-18 |
0,917 |
42 |
38 |
12 |
||||
Z3 |
1 |
88 178 216 |
0,25 0,50 0,75 |
80 82 79 |
0,182 0,146 0,185 |
352 356 288 |
64 52 53 |
347 353 282 |
4 13 30 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Średnie |
80 |
0,171 |
332 |
56 |
327 |
||||
Cosinus kąta ϕ wyznaczamy na podstawie pomiaru mocy ze wzoru P=UI cosϕ.
ϕ = arccosϕ =59
![]()
![]()
![]()
Elementy rezystancyjne i pojemnościowe traktujemy jako idealne, jako odbiornika indukcyjnego używamy cewkę o kącie fazowym zmierzonym w punkcie 4.
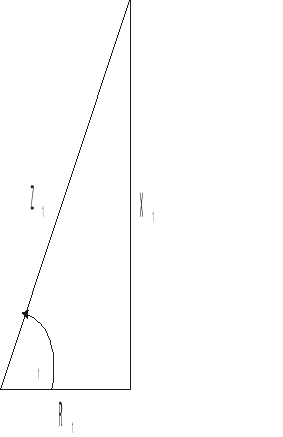
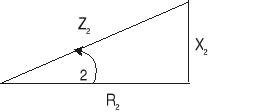
Trójkąty impedancji dla Z1, Z2, Z3:
Z1=237Ω Z2=42Ω Z3=332
R1=124Ω R2=38Ω R3=56
X1=204Ω X2=12Ω X3=327

φ1=580 φ2=170 φ3=800
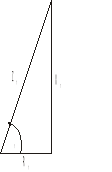
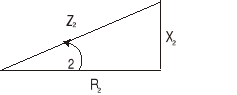
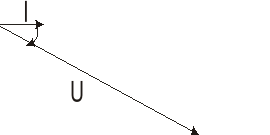
Rys 5. Trójkąty impedancji Z1, Z2, Z3

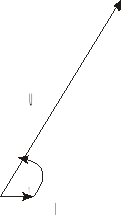
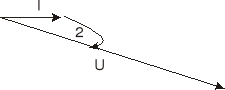
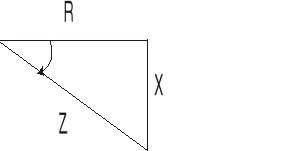
Rys. 6. Wykresy wskazowe impedancji Z1, Z2, Z3
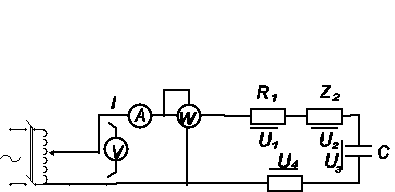
Szeregowe połączenie elementów RLC
Rys. 7. Schemat pomiarowy do badania układu szeregowego RLC
Lp. |
Pomiary |
||||||||
|
U |
I |
U1 |
U2 |
U3 |
U4 |
ϕ |
P |
|
|
V |
A |
V |
V |
V |
V |
° |
W |
|
1 2 3 |
69 140 147 |
0,2 0,3 0,4 |
8 11 15 |
42 62 83 |
59 89 118 |
30 44 58 |
-30 -50 -34 |
12 27 49 |
|
φśr |
-38 |
||||||||
Lp. |
Obliczenia |
|||||||||||
|
Z |
Z1 |
ϕ1 |
Z2 |
ϕ2 |
R2 |
X2 |
Z3 |
ϕ3 |
Z4 |
ϕ4 |
ZOBL |
|
Ω |
Ω |
° |
Ω |
° |
Ω |
Ω |
Ω |
° |
Ω |
° |
Ω |
1 2 3 |
345 467 368 |
40 37 38 |
0 0 0 |
210 207 208 |
58 58 58 |
111 110 110 |
178 175 176 |
295 297 295 |
90 90 90 |
150 147 145 |
0 0 0 |
319 |
Śr. |
393 |
39 |
0 |
208 |
58 |
110 |
176 |
296 |
90 |
147 |
0 |
|
![]()
![]()
Z1=R1 => cosφ1=1 => φ1=00
Z3=X3 => sinφ3=1 => φ3=900
Z4=R4 => cosφ4=1 => φ4=00
![]()
![]()
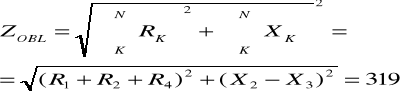
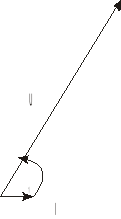
Z=393
R=R1+R2+R4=296
X=X2-X3= -120
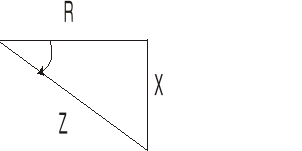
Rys. 8. Trójkąt impedancji układu RLC
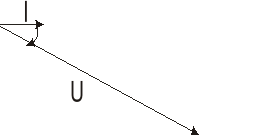
Rys. 9. Wykres wskazowy układu RLC
Wnioski
Kąt fazowy impedancji odczytany z oscyloskopu dwustrumieniowego nie zgadza się z odczytanym na oscyloskopie z odchyleniem poziomym i pionowym. Moim zdaniem wynika to prawdopodobnie z tego, iż wykres napięcia na oscyloskopie dwustrumieniowym powinien być przesunięty o π.
Badając impedancje zastępczą obserwujemy że cewka powoduje dodatnie przesunięcie fazowe, natomiast kondensator ujemne. Kondensator połączony szeregowo powoduje mniejsze przesunięcie niż połączony równolegle z rezystancją.
Ze względu na czytelność wykresy wskazowe impedancji Z1, Z2 Z3 nie są do końca proporcjonalne - wykres prądu jest wydłużony.
Wykresy wskazowe i trójkąty impedancji nie są narysowane we wspólnej skali - wynika to z stosunkowo dużych różnic wartości.
Badając szeregowe połączenie elementów RLCV licząc kąt φ z arctgφ z zależności cosφ=P/S nie jesteśmy w stanie określić czy kąt ma wartość dodatnią lub ujemną.
Obliczona impedancja układu szeregowego RLC jest niższa niż impedancja średnia Z - wynika to z przyjęcia zbyt małej dokładności obliczeń.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
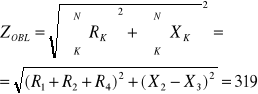

![]()
![]()
![]()
Wyszukiwarka