ELIPSOIDA obrotowa o odpowiednio dobranych parametrach jest znacznie lepszym przybliżeniem kształtu bryły ziemskiej niż kula. Elipsoidą odniesienia nazywamy elips. obrotową o odpowiednio dobranych parametr. i określonym usytuowaniu w bryle ziemskiej, na którą rzutowano punkty danej sieci geodezyjnej. W układzie współrzędnych prostokątnych XYZ umieszcza się elipsoidę obr. w taki sposób, że środek elips. pokrywa się z początkiem ukl. współ.; oś obrotu elipsoidy pokrywa się z osią Z ukl.współ.

Wsp. każdego pkt leżącego na pow. elipsoidy obrotowej spełniają równanie X²/a²+Y²/a²+Z²/b²=1 Kształt i wielkość elipsoidy obr. określają parametry: półosie a i b lub półoś a i spłaszczenie α [α=(a-b)/a] Zamiast α=(a-b)/a można posługiwać się mimośrodem elipsoidy e²=(a²-b²)/a²=α(2-α) II mimośród elips. e'²=(a²-b²)/b²,zależności między e² i α

e²=(a-b)(a+b)/ a²=(a-b)/a*(2-(a-b)/a)= α(2-α); także:b²/a²=(a²-(a²-b²)/a²=1- e²

wielkość II mimośrodu obliczamyze wzoru: e'²=(a²-b²)/b²= e'²=(a²-b²)/a²* a²/b²= e²/(1- e²)

równoleżnikiem punktu P jest ślad przecięcia pow. elipsoidy pł. przechodząca przez punkt P i równoległą do pł. równika. Ma kształt okręgu.

Południkiem punktu P jest ślad przecięcia elipsoidy pł. przechodzącą przez punkt P i oś obrotu elipsoidy.Ma kształt elipsy. Wpowadza się oś U i powstaje nowy, prostokątny układ UZ. Równanie połud. zawierającego pkt P w tym układzie to U²/a²+Z²/b²=1 Normalna n do elipsoidy leży w płaszcz. południka P.

Szerok. elipsoidalną B (sz.geodezyjna) punktu P jest kąt miedzy normalną n do powierzchni elipsoidy w punkcie P i płaszczyzną równika

Dł elipsoidalną L (dł.geodezyjna) punktu P jest kąt dwuścienny między płaszczyzną południka punktu P i pł. południka początkowego

Styczna do pow. elips. w pkt.P tworzy z dodatnim kierunkiem osi U kąt=90⁰+B co pozwala określić zależność pochodnej dZ/dU od szer.elipsoid. B.dZ/dU=tg(90⁰+B)= -ctgB po przekształc. i uwzględnieniu b²/a²=1-e² mamy U²=a²/1+(1-e²) tg²B Dla U≥0 mamy : U=(acosB) /√(1-e²sin²B), a promień równoleż nika pkt P r=U Współ. X i Y punktu P oblicz. X=UcosL; Y=UsinL, a współ. Z=[a(1-e²)sinB]/ √(1-e²sin²B)

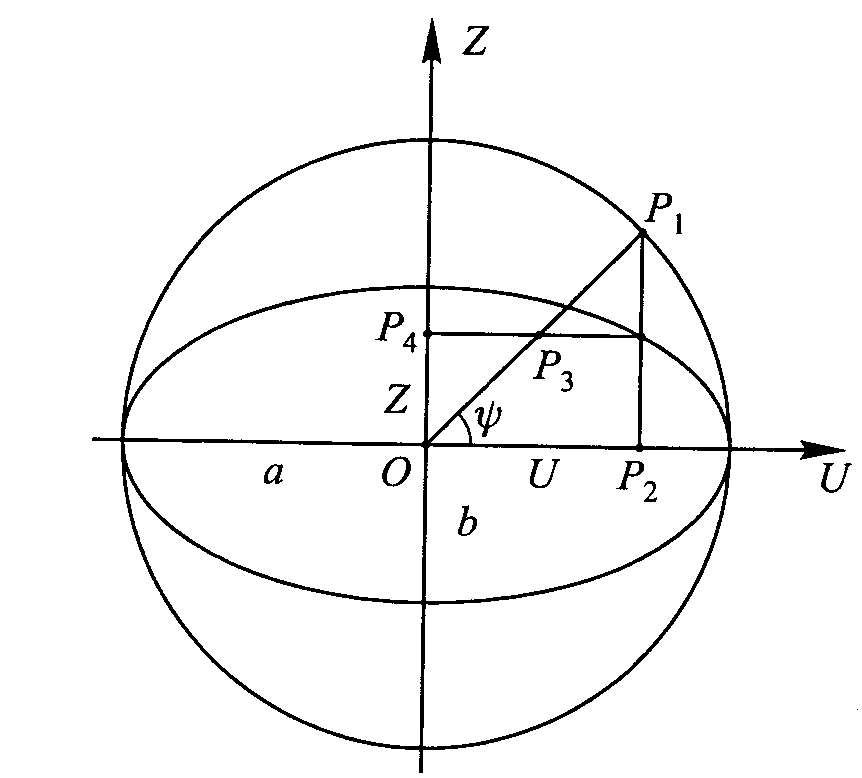
Szerokość zredukowana Przyjmujemy, że środek sfery pokrywa się ze środ. elips. obrot. Jeżeli przez pkt P leżący na elips. poprowadzimy prostą równoległą do osi obrotu Z, to punkt P₁ będzie rzutem punktu P na sferę. Kąt ψ zawarty między promieniem OP₁ a pł. równika będzie szerokością zredukowaną punktu P.

tgψ=[√(1a²)]×tgB

Przekroje normalne Przez punkt P leżący na danej, regularnej powierzchni można poprowadzić tylko jedną prostą prostopadłą do tej powierzchni zwaną normalną n. Wszystkie pł zawierające normalną n przecinają daną pow. wzdłuż krzywych zwanych przekrojami normalnymi w punkcie P. Krzywizny z reguły są zmienne. Spośród wszystkich przekrojów normalnych w danym punkcie wyróżniamy 2 przekroje główne. Jeden ma krzywiznę największą spośród krzywizn wszystkich przekrojów normalnych w danym punkcie, drugi zaś ma krzywiznę najmniejszą. Płaszczyzny przekrojów głównych przecinają się pod kątem prostym.

Jednym z przekrojów głównych elipsoidy obrotowej jest przekrój pł. południka, zwany przekrojem południkowym, a drugim - przekrój płaszczyzną prostopadłą do płaszcz. południka zwany przekrojem poprzecznym Długość promienia M krzywizny przekroju południkow

M=dS./dB,S-dł.południka,rożniczka dS zależy od dU i dZ czyli: dS.=√(dU²+dZ²),lub dS.=-dU√(1+(dZ/dU)²),znak minusa mówi o tym że ujemnemu przyrostowi dU odpowiada dodatni przyrost dS.,uwzględniając dZ/dU=-ctg B,to otrzymay: dS.=- dU√(1+ctg ²B)=-dU/sin B,zatem M=-dU/dB*1/sin B,

dU/dB=-a(1-e²)sin B/(1-e²sin ²B)^3/2,

Co ostatecznie daje nam wzór na M

M=[a(1-e²)]/(1-e²sin²B)^3/2.

Oba przekroje mają wspólną styczną w punkcie P, a płaszczyzny tych przekrojów tworzą kąt równy szerokości elipsoidalnej B, możemy zastosować tw. Meusniera : r=Ncos B,r to promień równoleżnika, zatemN=r/cosB, podst. r=U otrzymujemy długość promienia N krzywizny przekroju poprzecznego to N=a/(1-e²sin²B)^1/2 Zależność tę można wykorzystać do uproszczenia wzorów. określające wsp. prostokątne pkt leżącego na pow. elipsoidy: X=NcosBcosL; Y=NcosBsinL; Z=N(1-e²)sinB. Porównanie promieni M i N wskazuje, że pro. M jest najmniejszym a N największym promieniem krzywizny przekrojów normalnych w danym punkcie. Promień krzywizny dowolnego przekroju normalnego (wzór Eulera) 1/R_A=cos²A/M+sin²A/N. Średni promień krzywizny Q w danym punkcie elipsoidy definiujemy jako Q=1/2π₀∫^2πR_AdA. Obliczamy ze wzoru Q=√MN=(a√1-e²)/(1-e²sin²B)

Długość łuku południka Wzór wyjściowy dS=MdB S₁₂<60km z dok. 1mm S₁₂=M_s(B₂-B₁), M_s=M(B_Sr); Dla 60km<S₁₂<750km z dok. 1mm S₁₂=[(M₁+4M_s+M₂)*(B₂-B₁)]/6; Dla S₁₂>750km S₁₂=_B1∫^B2MdB=₀∫^B2MdB-₀∫^B1MdB

Pole powierzchni elipsoidy Elementarny czworobok krzywolinio. jest zawarty między dwoma południkami i równoleżnik. będącym wycinkiem powierzchni elipsoidy obrotowej.

Długości boków tego czworoboku są równe elementarnym długościom łuku południka (MdB) oraz równoleżnika (NcosBdL). Pole elementarnego czworoboku można obliczyć ze wzoru dP=MncosBdBdL. Pole czworoboku o wymiarach skończonych określa wzór P=_B1∫^B2_L1∫^L2MncosBdBdL. Pole całej powierzchni elipsoidy obrotowej to

P=a²(1-e²)4π[1+²/₃e²+³/₅e⁴+⁴/₇e⁶+...]

Odwzorowaniemjednej pow na drugą nazywamy każdą wzajemnie jednoznacz. odpowiedniość punktową między pow. nazywaną oryginałem a powierzchnią nazwaną obrazem Odwzorowanie nazywamy regularnym, gdy funkcje f i g spełniają warunki: a)każdej parze wartości parametrów u,v przyporządkowują jedną i tylko jedną parę wartości parametrów U,V b)są ciągłe i co najmniej 2-krotnie różniczkowalne c)są wzajemnie niezależne. W odwzorowaniu tym obrazem pkt jest pkt, krzywej - krzywa, kąta - kąt, obszaru - obszar. Jeżeli oryginałem jest cała pow.elipsoidy obrotowej lub jej część to rolę parametrów u,v odgrywają zwykle wsp.elipsoidalne B,L. Jeżeli rolę parametrów U,V odgrywają wsp. prostokątne x,y to f-cje odwzorowawcze mają postać x=x(B,L) y=y(B,L).Jeżeli położenie pkt. na pł. opisują wsp.biegunowe ρ,δ to f-cje odwzorow. mają postać δ=δ(B,L) ρ=ρ(B,L)

Skala główna mapy -zmniejszenie wszystkich elementów liniowych obrazu płaskiego w stałym stosunku m₀=1/m

Elementarna skala długości stosunek dł. ds nieskończenie małego łuku na obrazie do dł. ds odpowiadającemu mu łuku na oryginale m=ds/ds. Elementarna skala długości w danym odwzorowaniu zależy od współ. B,L określających położenie punktu, i od azymutu A elementu liniowego ds - m= m(B,L,A).Tylko w odwz. równokątnych zależy tylko od współ. punktu. Wartość skali długości mieści się w przedziale (0,∞).

Elementarny czworobok krzywoliniowy- jest zawarty między dwoma południkami i równoleż. będącym wycinkiem powierzchni elipsoidy obrotowej.

można traktować go jako figurę płaską leżącą w płaszczyźnie stycznej do elipsoidy w pkt.P₁ ponieważ różniczki dB i dL są nieskończenie małe. ds₁=MdB, ds₂=rdL=NcosBdL więc ds²=ds₁²+ds₂²=(MdB)²+(rdL)².

tg A=ds₂/ds₁=rdL/MdB

Kąt θ między południkiem a równoleżnikiem wynosi 90^o wzór na pole elementarnego czworoboku wynosi dP=ds₁ds₂=M*rdBdL

Obrazem elementu liniowego ds będzie element ds wyrażony wzorem ds²=dx²+dy² H²=EG-F² Posługując się wielkościami E,F,G gdzie E=(δx/δB)²+(δx/δ B)²F=(δx/δB*δx/δL)+ (δy/δB*δy/δL)G=(δx/δL)²+(δy/δL)² H= (δx/δB*δy/δL)-(δx/δl*δx/δB) Łatwo można spr.że H²=EG-F² Posługując się wielkościami E,F,G możemy obl. długość elementu liniowego ds²=Edb²+ 2FdbdL +GdL² Długość elementarnego łuku południka otrzymamy przyjmując w odwzorowaniu dL=0 to ds₁=(√E)dB a długość równoleżnika ds₂=(√G)dL. Skala dł. w kierunku południków m_B=ds₁/ds₁=(√E)/M. a w kierunku równoleż. m_L=ds₂/ds₂=(√G)/r Kątψ₁jest szczególnym przypadkiem kątaψ gdy dL=0 tgψ₁= (δy/δB)/(δx/δB) ψ₂ jest natomiast szczególnym przypadkiem ψ gdy dB=0 tgψ₂= (δy/δL)/(δx/δL) Wynika że kąt θ będący obrazem kąta θ=90⁰ równa się różnicy ψ₂-ψ₁ więc tgθ=tg(ψ₂-ψ₁)

Odwzorowanie jest równokątne, jeżeli w każdym punkcie odwzorowywanego obszaru dowolny azymut A odwzorowuje się bez zniekształcenia, tzn. A≡A. Warunki równokątności F=0 i jednocześnie (E/H) *(r/M)=1. ctgA=(m_BctgA/m_Lsinθ)+ctgθ

Po przekształceniach: odwz. jest równokątne jeżeli spełnione są jednocześnie dwa warunki: 1.obrazy południków przecinają się z obrazami równoleżników pod kątem prostym θ=90^o; 2.w każdym punkcie skala długości w kierunku południków jest równa skali długości w kierunku równoleżników m_B=m_L

Postacie różniczkowe warunku równokątności ∂x/∂L=-r∂y/M∂B; ∂y/∂L=+r∂x/M∂B

Wz na pole czworoboku elementarnego dP=ds₁ds₂sinθ i na skalę pól

P=(ds₁ds₂sinθ)/(ds₁ds₂).

Przy odwzorowaniach równokątnych skale dł. nie zależą od kierunku.

Warunek równopolowości Odwzorowanie jest równopolowe jeżeli w każdym pkt odwzorowywanego obszaru spełniony jest warunek p=1 czyli m_Bm_Lsinθ=1 lub H=Mr Gdy θ=90^o to m_Bm_L=1

Kierunki główne Na powierzchni elipsoidy są dwi krzywe k1 i k2,przecinają się pod kątem 90st. Na obrazie krzywe te przetną się pod kątem różnym od 90 zwiększając w sposób ciągły azymut A1 zauważamy, że przy pewnej wartości tego azymutu kąt między obrazami kierunków osiąga wartość minimalną <90st. I max >90.Oznacza to, że nastąpił taki moment w którym kąt ten =90. istnieją dwie wart. Azym. A_g czyli A_g1 i A_g2, azymuty te określają położenie K1 i K2 =90, na oryginale i obrazie.

I tw. Tissota W każdym odwzorow. regularnym, nie będącym odwzorow. równokątnym, istnieje na oryginale dokładnie jedna siatka ortogonalnych linii parametrycznych, której obrazem jest także siatka ortogonalna. Kierunki tej siatki nazywamy kierunkami głównymi. Nie są one określone gdy odwzorowanie jest równokątne. Gdy obrazy południków i równoleż. przecinają się pod kątem prostym (θ=90^o) wówczas kierunki główne pokrywają się z nimi. Wzory na azymuty w kierunkach głównych oryginału i obrazu tg2A_g=(2m_Bm_Lcosθ)/(m_B²-m_L²); Po przekształceniach tg2A_g=(m_L²sin2θ)/(m_B²+m_L²cos2θ)

Skala długości w kierunkach głównych.

Kwadrat skali długości można wyrazić wzorem:m²=ds²/ds²=(EdB²+2F dBdL+GdL²)/(M²dB²+r²dL²) , dzielimy licznik i mianownik przez dL² mamy: m²=E(dB/dL)²+2F(dB/dL)+G/M²(dB/dL)²+r² (#). Stosunek dB/dL zależny od azymutu A elementu ds obl.: dB/dL=r/M ctgA ,podstawiając to do wz.(#) mamy:

m²=[E*r²/M²ctg²A+2F*r/MctgA+G]/[r²ctg²A+r²] , ponieważ r²ctg²A+r²=r²(ctg²A+1)=r²/sin²A ostatecznie otrzymujemy :m²=E/M²cos²A+F/Mr sin2A+G/r²sin²A ,z wz.wynika że skala dł. m zależy od E,F,G i azym. A . Skala dł. w kierunku południków: m_B=√E /M E=(δx/δB)²+(δy/δB)², Skala dł. w kier. równoleżników: m_L=√G /r G=(δx/δL)²+(δy/δL)². Z powyższych wzorów otrzymujemy m²= m_B²cos²A+m_Bm_Lcosθsin2A+m_L²sin²A Skala długości jest funkcją okresową azymutu o okresie 180^o. W pełnym zakresie azymutów, od A=0^o do A=360^o, skala m będzie osiągała 2 razy tę samą wartość max i 2 razy tę samą wartość min

Ekstremalne skale długości występują w kierunkach głównych tg2A_e=(m_Bm_Lsinθ)/(m_B²-m_L²) e -ekstremalne wartości skali W odwz. równokątnych kierunki gł. nie są określone dlatego skala dł.w danym pkt. nie zależy od kierunku

Elipsa zniekształceń RYS 28,29

pamiętaj o jednostce do II Tissota

Rys.

(wskaźnica Tissota) II tw Tissota „Obrazem graficznym skal długości we wszystkich kierunkach wyprowadzonych z danego punktu jest elipsa o półosiach równych skalom długości w kierunkach głównych”.

Wskaźnica Tissota ma postać (x^'2/a²)+(y^'2/b²)=1Rys Określenie skali długości jako funkcji kąta B opisuje wzór m²=a²cos²B+b²sin²B Do równania elipsy podstawiamy wartości współ. x'=ds*cosB i y'=ds*sinB Uwzględniając ds/ds=m to otrzymujemy 1/m²=(cos²B/a²)+(sin²B/b²) Skale a,b otrzymujemy z zależności

a+b=√(m_B²+2m_Bm_L sinθ +m_L²);

a-b=√(m_B²-2m_Bm_Lsinθ+m_L²)

Wsp. izometryczne Zakładamy, że pow. opisana jest równaniami X=X(u,v); Y=Y(u,v); Z=Z(u,v) Długość elementarnego łuku ds na tej powierzchni można wyrazić wzorem(*)ds²=Edu²+2Fdudv+Gdv² Współ. krzywoliniowe u,v są współ. izometrycznymi jeżeli długość elementarnego łuku ds na danej powierzchni można wyrazić wzorem (**) ds²=μ(du²+dv²), gdzie μ jest dowolną, dodatnią funkcją u,v Gdy porównamy wzory (*)i(**) to stwierdzimy, że jeżeli współ. u,v są współ. izometrycznymi, to zachodzą zależności F=0; E=G=μ² Współ. krzywoliniowe u,v są współ. izometrycznymi jeżeli spełniają 2 warunki: 1.Siatka współ. u,v jest siatką ortogonalną 2.Przesunięcie ds wywołane zmianą współ. u o du=ε, jest równe przesunięciu ds wywołanemu zmianą współ. v o dv=ε, gdzie ε jest nieskończenie małą dowolnie obraną liczbą.

KLASYFIKACJA ODWZ. KARTOGRAFICZ:

1.Ze względu na charakter występujących zniekształceń odwzorow: równokątne, równopolowe, równoodległościowe w jednym z kierunków głównych, dowolne. 2.Ze wzgl. Na kształt siatki kartograficznej: azymutalne, walcowe, stożkowe. 3. Ze wzgl. na sposób przyłożenia pow.rzutowania: normalne, ukośne, poprzeczne.

Klasyfikacja odwzor. ze względu na kształt siatki kartogr. czyli kształt obrazu siatki geograficznej:Rys

1.Odwz.azymutalne.

Obrazami południków są półproste zbiegające się w obrazie bieguna ziemskiego. Kąty między obrazami południków nie ulegają zniekształceniu i są równe różnicom długości geograficznych południków.

λ=0⁰ P(δ,ρ)

Obrazem równoleż. są okręgi współśrodkowe, których środek jest na obrazie bieguna. Równania ogólne odwz. azymutalnych mają postać w ukł. wsp. biegunowych: ρ=ρ(φ), δ =λ. 2.Odwz.walcowe.

Obrazami południków są proste lub odcinki równoległe względem siebie i prostopadłe do prostoliniowego obrazu równika. Odległość między obrazami dwóch danych południków jest proporcjonalna do różnicy ich długości geograficznych. Obrazami równoleż. są odcinki równoległe do obrazu równika.

Równanie tych odwz. w ukł. wsp. prostokątnych x,y utworzonym przez obrazy południka początkowego i równika: X = x(φ), Y = Cλ.

3.Odwz. stożkowe.

Obrazami równoleż. są łuki okręgów współśrodkowych, obrazami południków są odcinki lub półproste prostopadłe do obrazów równoleżników. Kąty między obrazami połud. są proporcjonalne do różnicy długości geograficznych południków.

Równanie ogólne: ρ = ρ(φ), δ = Cλ.

4.Odwz. pseudoazymtal.

Obrazami równol. są okręgi współśrodkowe, których środkiem jest obraz bieguna ziemskiego. Obrazami połudn. są krzywe zbiegające się w obrazie bieguna, symetryczne wzgl. prostoliniowego obrazu wybranego południka. Równanie ogólne: ρ = ρ(φ), δ = δ(λ,φ).

5.Odwz.pseudowalcowe

Obrazem równika i wybranego południka środkowego są wzajemnie prostopadłe odcinki linii prostych. Obrazami równoleż. są odcinki linii prostych, równoległe do obrazu równika. Obrazami połudn. są odcinki krzywych tworzące obraz symetryczny względem obrazu południka środkowego. Obrazem bieguna jest punkt lub odcinek. Równanie ogólne: x = x(φ), y = y(φ,λ).

6.Odwz.pseudostożkowe

Obrazami połudn. są krzywe symetryczne wzgl. prostoliniowego obrazu połudn. środkowego, zbiegające się w obrazie bieguna. Obrazami równol. są łuki okręgów współśrodkowych, których środek leży na tej prostej, na której leży obraz połudn. środkowego.

Równanie ogólne: q = const, ρ = ρ(φ), δ = δ(φ,λ). Mogą być traktowane jako szczególne przypadki odwz. pseudostożkowych, występujących wtedy, gdy pkt. W znajduje się w obrazie bieguna Pn.

7.Odwz.wielostożkowe.

Obrazami równol. są łuki okręgów niewspółśrodkowych. Środki tych okręgów leżą na prostej przechodzącej przez odcinek będący obrazem południka środkowego. Obrazem połudn. są łuki krzywych tworzące obraz symetryczny względem obrazu połudn. środkowego. Równanie ogólne: q = q(φ), ρ = ρ(φ), δ = δ(φ,λ).

8.Odwz.koliste.

Stosowane do przedst. w postaci koła obrazu całej powierzchni kuli ziemskiej lub obrazu powierzchni wybranej półkuli. Obrazem równika i południka środkowego są wzajemnie prostopadłe odcinki linii prostych. Obrazami południków są łuki okręgów tworzące obraz symetryczny względem obrazu obrazu południka środkowego. Obrazami równol. są łuki okręgów tworzące obraz symetryczny wzgl. obrazu równika. Środki okręgów znajdują się na tych prostych, na których leżą obrazy południka środkowego i równika. Równanie ogólne: ρ_x = ρ_x(φ), q_x = q_x(φ), ρ_y = ρ_y(λ), q_y = q_y(λ).

---