6.Dźwigar

6.1.Dźwigar główny środkowy

6.1.1.Zestawienie obciążeń

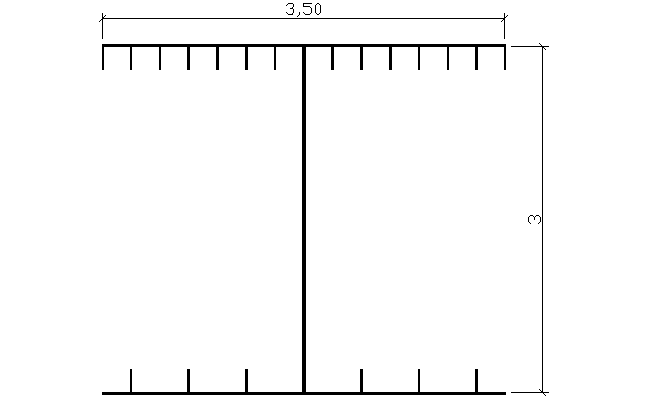
---------------- REGIONS ----------------

Area: 0.2672

Perimeter: 28.0480

Bounding box: X: -1.7500 -- 1.7500

Y: -1.6247 -- 1.4193

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia: X: 0.4982

Y: 0.2172

Product of inertia: XY: 0.0000

Radii of gyration: X: 1.3655

Y: 0.9016

Principal moments and X-Y directions about centroid:

I: 0.2172 along [0.0000 -1.0000]

J: 0.4982 along [1.0000 0.0000]

• Obciążenia stałe

• ciężar własny

charakterystyczne

q_dK = 78,5kN/m³ * 0,2672m² = 20,975 kN/m

obliczeniowe

max q_dO = q_bK*1,2 = 25,17 kN/m

min q_dO = q_bK*0,9 = 18,877 kN/m

• ciężar poprzecznic i wspornika bez płyty

patrz pkt.4.5.5. =>A=0,009m²,dł.L=2*3,5m+2*3,36m=13,72m,rozstaw a = 2m

charakterystyczne

q_PK = 78,5kN/m³ *0,009m² /2m= 0,353 kN/m²

obliczeniowe

max q_PO = q_PK*1,5 = 0,53 kN/m²

min q_PO = q_PK*0,9 = 0,32 kN/m²

• ciężar żeber usztywniających środnik

przyjęto 3000x300x20 => V = 0,018 m³ , rozstaw a = 2m

charakterystyczne

q_ŻK = 78,5kN/m³ *2* 0,018m³/2m= 1,413 kN/m

obliczeniowe

max q_ŻO = q_ŻK*1,5 = 2,119 kN/m

min q_ŻO = q_ŻK*0,9 = 1,272 kN/m

• ciężar nawierzchni

charakterystyczne

q_bK = 20kN/m³ * 0,09m = 1,8 kN/m²

obliczeniowe

max q_bO = q_bK*1,5 = 2,7 kN/m²

min q_bO = q_bK*0,9 = 1,62 kN/m²

• ciężar izolacji

charakterystyczne

q_iK = 14kN/m³ * 0,01m = 0,14kN/m²

obliczeniowe

max q_iO = q_bK*1,5 = 0,21kN/m²

min q_iO = q_bK*0,9 = 0,126kN/m²

• ciężar kapy chodnikowej na wsporniku

charakterystyczne

q_kK = 20kN/m³ * 0,22m = 4,4kN/m²

obliczeniowe

max q_kO = q_kK*1,5 = 6,6kN/m²

min q_kO = q_kK*0,9 = 3,96kN/m²

• ciężar bariery i poręczy

charakterystyczne

q_BK = 4kN/m

obliczeniowe

max q_Bo = q_BK *1,5 = 6kN/m

min q_Bo = q_BK *0,9 = 3,6kN/m

• ciężar gzymsu

charakterystyczny

q_GK = 20kN/m³*0,5m*0,2m=2,0kN/m

obliczeniowy

max q_GO = q_GK *1,5 = 3,0 kN/m

min q_GO = q_GK *0,9 = 1,8 kN/m

Sumy obciążeń stałych

• Obciążenie dociążające dźwigar

ciężary max obl. : 2*poprzecznic+nawierzchni+izolacji

q_DO = (2*0,53+2,7+0,21)kN/m² = 3,97 kN/m²

• Obciążenie odciążające dźwigar

ciężary min obl : wspornika +izolacji+ kapy chodnikowej

q_OD = (0,32+0,126+3,96)kN/m² = 4,406 kN/m²

ciężary min obl : bariery , poręczy , gzymsu

q_b = 3,6 kN/m

q_p = 3,6 kN/m

qg =1,8 kN/m

• Obciążenie własne dźwigara

ciężary max obl. : dźwigara + żeber

Q = (25,17+2,119)kN/m = 27,289 kN/m

• Obciążenia normowe dynamiczne

• równomiernie rozłożone

charakterystyczne

q_K = 4kN/m²

obliczeniowe

q_O = 4kN/m²*1,5 = 6 kN/m²

• pojazd K

charakterystyczne

K = 800 kN rozpiętość przęsła L =60m

 = 1,35 - 0,005L = 1,05

K_k = 800 kN * 1,05 = 840 kN

obliczeniowe

max K_o = 840 kN * 1,5 = 1260 kN

na koło

P_c = K_o/8 = 1260 kN / 8 = 157,5 kN

6.1.2.Rozdział poprzeczny obciążenia metodą sztywnej

poprzecznicy

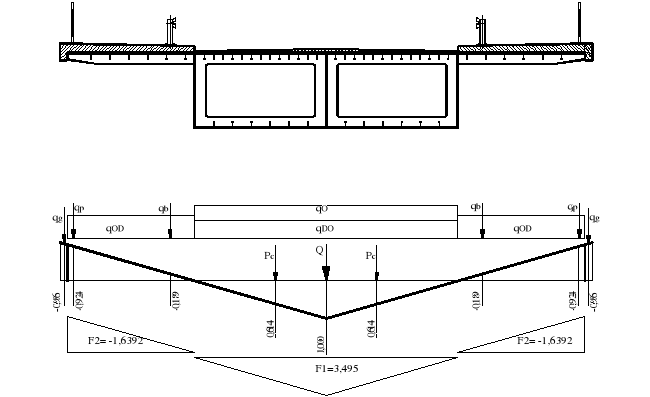
6.1.3.Max obciążenie dźwigara środkowego

Obciążenie stałe rozłożone na całej długości przęsła

q = (q_O+q_DO)*F1 - q_OD*2*F2 - 2*q_p*0,924 - 2*q_g*0,996 - 2*q_b*0,189 + Q*1 =

(6+3,97)kN/m²*3,495m - 4,406 kN/m²*2*1,6392m - 2*3,6kN/m*0,924-

2*1,8kN/m*0,996 - 2*3,6kN/m*0,189 + 27,289kN/m = 36,09 kN/m

Obciążenie ruchome od pojazdu K na oś

P = 2* P_c * 0,614 = 2*157,5kN*0,614 = 193,41 kN

6.1.4.Moment max

Linia wpływu momentu przęsłowego

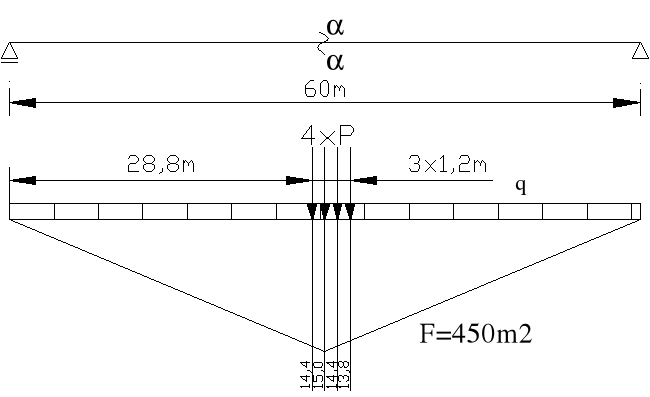
M_max = q*F + P* = 36,09 kN/m * 450m² + 193,41 kN*(15+2*14,4+13,8) = 27381 kNm

6.1.5.Sprawdzenie naprężeń normalnych

Przyjęcie długości współpracującej płyty

b/L = 3,5 m/60m = 0,06

F_z/bg = 0,116m²/(3,5m*0,044m) = 0,75

odczytano poprzez interpolacje  = 0,72

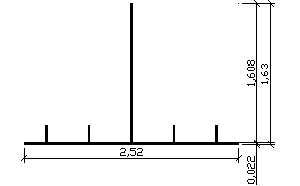
b₀ = b *  = 3,5m * 0,72 = 2,52m

Przekrój skorygowany nośny

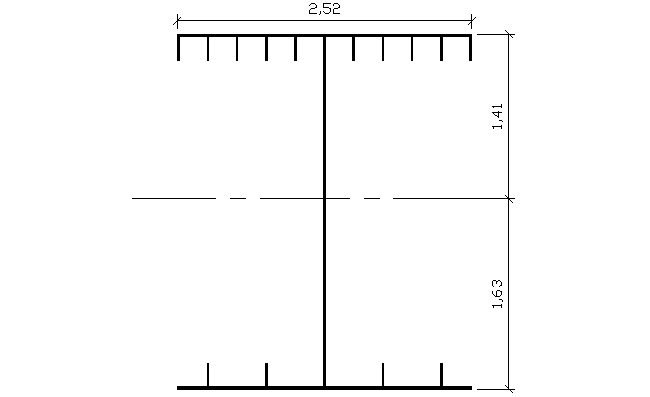
---------------- REGIONS ----------------

Area: 0.2101

Perimeter: 21.7280

Bounding box: X: -1.2600 -- 1.2600

Y: -1.6340 -- 1.4100

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia: X: 0.3725

Y: 0.0849

Product of inertia: XY: 0.0000

Radii of gyration: X: 1.3316

Y: 0.6358

Principal moments and X-Y directions about centroid:

I: 0.0849 along [0.0000 -1.0000]

J: 0.3725 along [1.0000 0.0000]

Wx = Jx/z = 0,3725m⁴/1,63m = 0,22853m³

Sprawdzenie naprężeń

σ = M_max/Wx = 27,381 MNm/0,22853m³ = 119,81 Mpa < R = 195 Mpa

Warunek spełniony

6.1.6.Max siła tnąca

Linia wpływu siły tnącej przy podporze

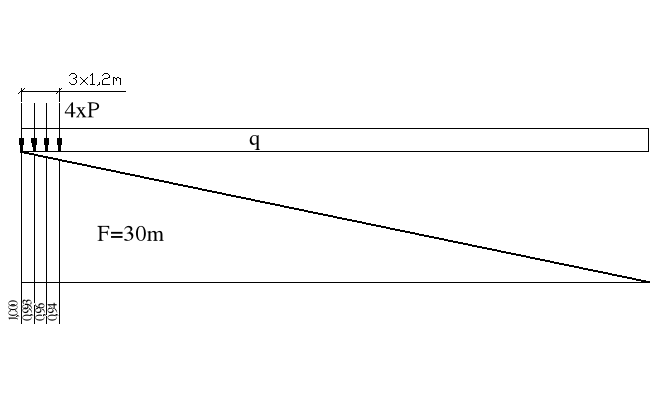
T_max = q*F+P* = 36,09 kN/m*30m+193,41 kN*(1+0,993+0,96+0,94)= 1835,645 kN

6.1.7.Sprawdzenie napręrzeń stycznych w środniku

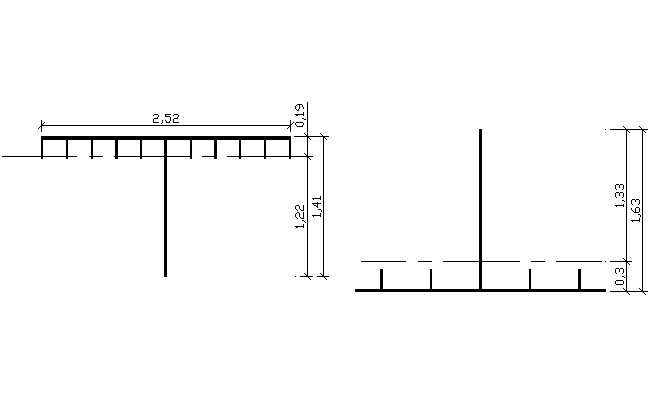
---------------- REGIONS ---------------- ---------------- REGIONS ----------------

Area: 0.1112 Area: 0.0989

S₁=A*z₁= 0,1112m²*1,22m = 0,13566m³

S₂=A*z₂= 0,0989m²*1,33m = 0,13154m³

 = T_max*S₁/(Jx*t_ś)=1835,645kN*0,13566m³/(0,3725m⁴*0,02m)= 33,43 Mpa < R_t = 115 MPa

6.1.7.Sprawdzenie stateczności lokalnej środnika przy ścinaniu

b = 3m t = 0,02m

 = b/t = 3/0,02 = 150

e = 2m

 = e/b = 2m/3m = 0,667 < 1 => 1/ = 1,5 =>  = e/t = 2m/0,02m = 100 => K_t = 1660

_p = K_t/(R)^1/2 = 118,875

/_p = 100/118,875 = 0,841 => interpolacja m_st = 1,111

 = 33,43 MPa < R_t/m_st = 156/1,111 = 140,41 MPa

Warunek spełniony

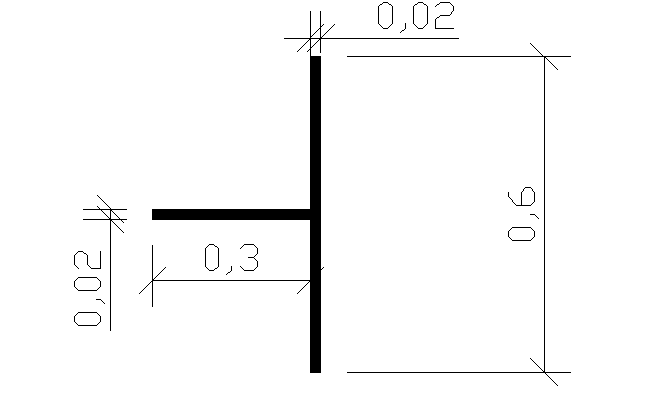
6.1.8.Sprawdzenie żeber nad podporą

Jz >= 3b_tg³ = 3*3m*0,02m³ = 0,072*10^-3m⁴

b_ż >= b_t/30+0,04m = 3m/30+0,04m = 0,14m

g_ż >= b_ż/15 = 0,3m/15 = 0,02m

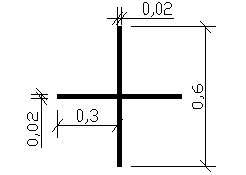
---------------- REGIONS ----------------

Area: 0.0240

Perimeter: 2.4400

Bounding box: X: -0.3100 -- 0.3100

Y: -0.3000 -- 0.3000

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia:X: 0.0004

Y: 0.0004

Product of inertia: XY: 0.0000

Radii of gyration: X: 0.1225

Y: 0.1287

Principal moments and X-Y directions about centroid:

I: 0.0004 along [1.0000 0.0000]

J: 0.0004 along [0.0000 1.0000]

l_w= 3m , i_x = (Jx / A)^1/2 = (0,0004m⁴/0,024m²)^1/2 = 0,1291m

=l_w/i_x = 3m/0,1291m = 23,24

_p= 118(200/R)^1/2 = 118(200/195)^1/2 = 119,5

 _p = 23,24/119,5 = 0,195 => interpolacja m_w = 1,05

T_max = 1835,645 kN

F_ż = 0,024m²

σ_c = T_max*m_w/F_ż = 1835,645 kN*1,05 / 0,024m² = 80,31 MPa < R = 195 MPa

Warunek spełniony

6.1.9.Dobranie spoin pionowych żeber

T_max = 1835,645 kN

_II = T_max/al. < sR => a > T_max/(sR*l ) = 1,835645 MN / (0,8*195MPa*4*2,9m)

= 0,001m

przyjęto spoinę pachwinową na wysokości środnika 2,9m o a = 4mm

6.1.10.Sprawdzenie żeber na docisk powierzchniowy

powierzchnia dociskowa żeber A_żd = (0,25m*0,02m)*2 = 0,01m²

σ_c = T_max/A_żd = 1,835645 MN/0,01m² = 183,56 MPa < R = 195 MPa

6.1.11.Dobranie spoin łączących pasy dźwigara ze środnikiem

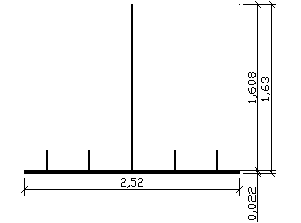
Sx = (0,022*2,52+4*0,02*0,2)m²*1,608m

= 0,11488 m³

 = T_max*Sx/(Jx*2*a) < R_t => a > T_max*Sx/(Jx*2* R_t)

a > 1,835645 MN*0,11488m³/(0,3725m⁴*2*115MPa)

a > 0,0025m

Przyjęto spoinę pasa dolnego i górnego o a = 4 mm

6.1.12.Sprawdzenie spoin montażowych środnika

M_max = 27,381 MNm

wymiary środnika

h = 3m , t = 0,02m

charakterystyki

Jx = 0,3725m⁴

z = 1,608m => Wx = Jx/z = 0,3725m⁴/1,608m = 0,23165m³

σ = M_max/Wx = 27,381 MNm/0,23165m³ = 118,2 MPa < sR = 0,85*195MPa = 165,75 MPa

Warunek spełniony

Przyjęto spoinę czołową w V o g = 20 mm

6.2.Dźwigar główny skrajny

6.2.1.zestawienie obciążeń

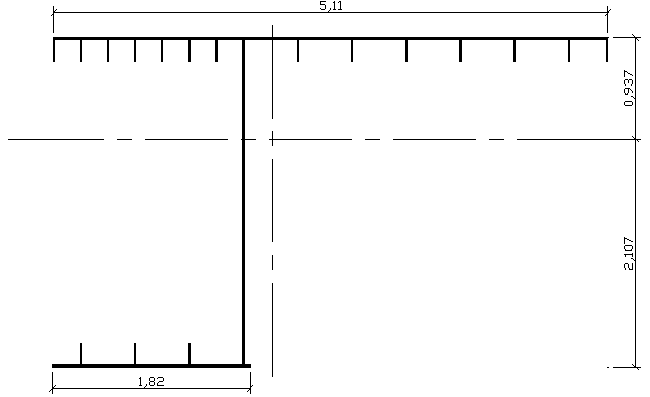
---------------- REGIONS ----------------

Area: 0.2587

Perimeter: 26.7080

Bounding box: X: -2.0295 -- 3.0905

Y: -2.1040 -- 0.9400

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia: X: 0.3962

Y: 0.4639

Product of inertia: XY: 0.1897

Radii of gyration: X: 1.2376

Y: 1.3391

Principal moments and X-Y directions about centroid:

I: 0.2374 along [0.7667 0.6420]

J: 0.6227 along [-0.6420 0.7667]

• Obciążenia stałe

• ciężar własny

charakterystyczne

q_dK = 78,5kN/m³ * 0,2587m² = 20,308 kN/m

obliczeniowe

max q_dO = q_bK*1,2 = 24,37 kN/m

min q_dO = q_bK*0,9 = 18,277 kN/m

• ciężar żeber usztywniających środnik

przyjęto 3000x300x20 => V = 0,018 m³ , rozstaw a = 2m

charakterystyczne

q_ŻK = 78,5kN/m³ * 0,018m³/2m= 0,707 kN/m

obliczeniowe

max q_ŻO = q_ŻK*1,5 = 1,06 kN/m

min q_ŻO = q_ŻK*0,9 = 0,636 kN/m

• obciążenia jak w pkt. 6.1.1.

Sumy obciążeń

Q = max q_dO + max q_ŻO =(24,37+1,06)kN/m = 25,43 kN/m

q_do = 2*max q_PO+ max q_bO+ max q_iO+ q_O = 2*0,53kN/m²+

2,7 kN/m²+0,21 kN/m²+6 kN/m² = 9,97 kN/m²

q_od = 2*min q_PO+ min q_bO+ min q_iO = 2*0,32 kN/m²+

1,62 kN/m²+0,126 kN/m² = 2,386 kN/m²

max q_ka = max q_PO+ max q_iO+ max q_kO = 0,53 kN/m²+

0,21 kN/m²+6,6 kN/m² = 7,34 kN/m²

min q_ka = min q_PO+ min q_iO+ min q_kO = 0,32 kN/m² + 0,126 kN/m²+

3,96 kN/m² = 4,406 kN/m²

q_tO = 2,5kN/m²*1,3 = 3,25 kN/m²

max q_b = max q_p = 6 kN/m²

min q_b = min q_p = 3,6 kN/m²

max q_g = 3 kN/m²

min q_g = 1,8 kN/m²

P_c = 157,5 kN

6.2.2.Rozdział poprzeczny obciążenia metodą sztywnej

poprzecznicy

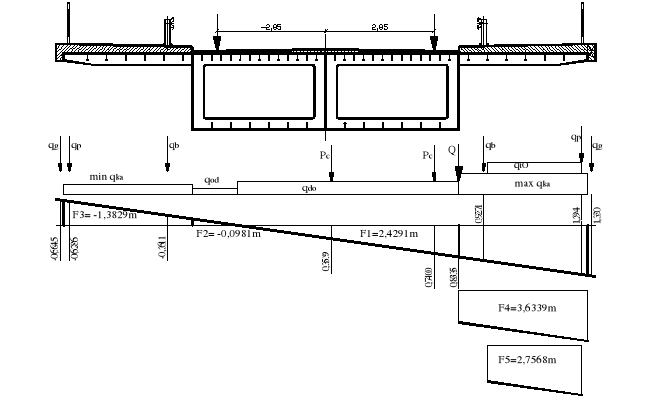
q = q_do*F1+max q_ka*F4+q_tO*F5+Q*0,8335+max q_g*1,33+max q_p*1,294+max q_b*0,9271 -

min q_od*F2 - min q_ka*F3 - min q_b*0,2611 - min q_p*0,6286 - min q_g*0,6645 =

9,97 kN/m²*2,4291m+7,34kN/m²* 3,6339m+3,25kN/m²*2,7568m+25,43kN/m

*0,8335 + 3kN/m*1,33+6kN/m*(1,294+0,9271) - 2,386kN/m*0,0981 - 4,406kN/m*

1,3829 - 3,6kN/m*(0,2611+0,6286) - 1,8kN/m*0,6645 = 68,637 kN/m

P = P_c*(0,3539+0,74) = 157,5kN*1,0939 = 172,29 kN

6.2.3.Max moment

Linia wpływu momentu przęsłowego

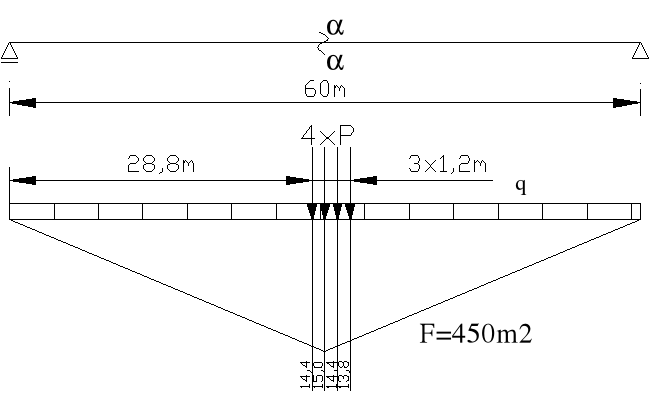
M_max= q*F + P* = 68,637kN/m*450m²+172,29 kN*(15+2*14,4+13,8)m= 40810,554 kN

6.2.4.Sprawdzenie naprężeń normalnych

Przyjęcie długości współpracującej płyty

b_L = 1,75m b_P = 3,36m

b_L/L = 1,75 m/60m = 0,03 b_P/L = 3,36 m/60m = 0,056

F_z/bg = 0,1062m²/(5,11m*0,022m) = 0,94

odczytano poprzez interpolacje _L = 0,85 _P = 0,732

b_0L = 1,75m*0,85 = 1,488m

b_0P = 3,36m*0,85*0,732 = 2,09m => b₀ = 3,578m

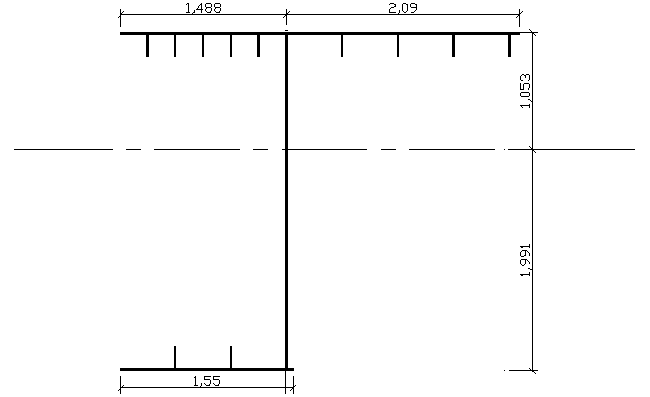
---------------- REGIONS ----------------

Area: 0.2036

Perimeter: 20.7000

Bounding box: X: -1.4815 -- 2.0965

Y: -1.9883 -- 1.0557

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia: X: 0.3187

Y: 0.1494

Product of inertia: XY: 0.0839

Radii of gyration: X: 1.2512

Y: 0.8566

Principal moments and X-Y directions about centroid:

I: 0.1148 along [0.3807 0.9247]

J: 0.3532 along [-0.9247 0.3807]

Wx = Jx/z = 0,3187m⁴/1,991m = 0,1601m³

σ = M_max/Wx = 40,81 MNm/0,1601m³ = 254,9 Mpa > R = 195 MPa

Warunek niespełniony

Zmiana przekroju nośnego , zamontowano chodnik służbowy aby można było korzystać z włazów konserwatorskich.

6.2.5.Przyjęcie przekroju z chodnikiem służbowym

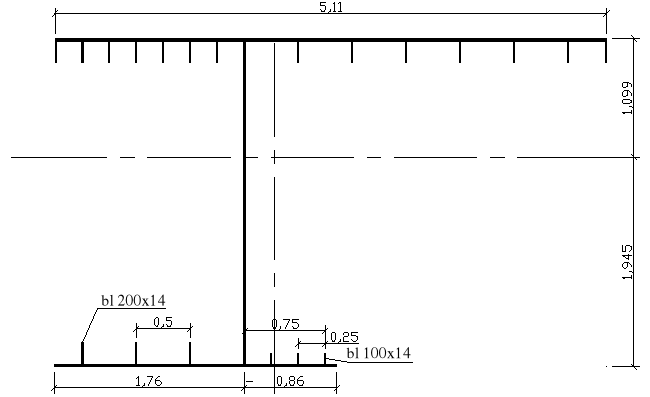
---------------- REGIONS ----------------

Area: 0.2805

Perimeter: 28.9080

Bounding box: X: -2.0449 -- 3.0751

Y: -1.9422 -- 1.1018

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia: X: 0.4833

Y: 0.4658

Product of inertia: XY: 0.1814

Radii of gyration: X: 1.3127

Y: 1.2887

Principal moments and X-Y directions about centroid:

I: 0.2929 along [0.6898 0.7240]

J: 0.6561 along [-0.7240 0.6898]

Dodatkowe obciążenia

Wyposażenie chodnika :

• nawierzchnia

charakterystyczne

q_hk= 20 kN/m³*0,15m = 3 kN/m²

obliczeniowe

max q_hO = q_hk*1,5 = 4,5 kN/m²

min q_hO = q_hk*0,9 = 2,7 kN/m²

• ciężar własny

charakterystyczne

q_dK = 78,5kN/m³ * 0,2805m² = 22,02 kN/m

obliczeniowe

max q_dO = q_bK*1,2 = 26,424 kN/m

min q_dO = q_bK*0,9 = 19,82 kN/m

• bariera na chodniku

max q_b = 6 kN/m²

min q_b = 3,6 kN/m²

6.2.6.Korekta obciążeń na rozdział poprzeczny obciążenia

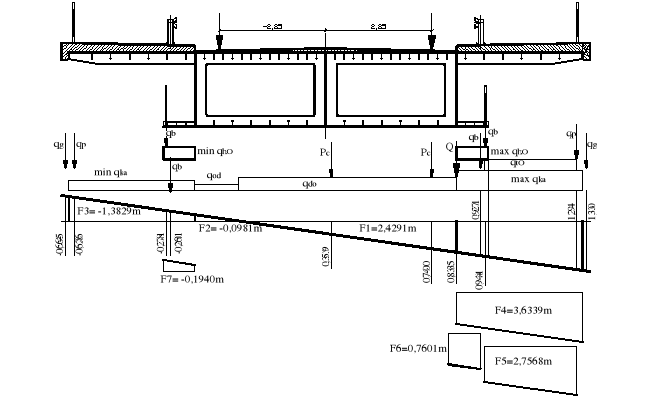
q = q_do*F1+max q_ka*F4+q_tO*F5+Q*0,8335+max q_g*1,33+max q_p*1,294+max q_b*0,9271+

max q_hO*F6 + max q_b* 0,9441- min q_hO*F7 - min q_b *0,2781 - min q_od*F2 - min q_ka*F3

- min q_b*0,2611 - min q_p*0,6286 - min q_g*0,6645 =

9,97 kN/m²*2,4291m+7,34kN/m²* 3,6339m+3,25kN/m²*2,7568m+26,424kN/m

*0,8335 + 3kN/m*1,33+6kN/m*(1,294+0,9271) + 4,5kN/m²*0,7601m+6kN/m*0,9441

- 2,7kN/m²*0,194m - 3,6kN/m * 0,2781- 2,386kN/m*0,0981 - 4,406kN/m*

1,3829 - 3,6kN/m*(0,2611+0,6286) - 1,8kN/m*0,6645 = 77,025 kN/m

P = P_c*(0,3539+0,74) = 157,5kN*1,0939 = 172,29 kN

6.2.7.Korekcja max momentu

M_max = q*F+P* = 77,025kN/m*450m²+172,29 kN*(15+2*14,4+13,8)m = 44085,154kNm

M_max = 44,085 MNm

6.2.8.Sprawdzenie naprężeń w przekroju skorygowanym z otworami

włazowymi

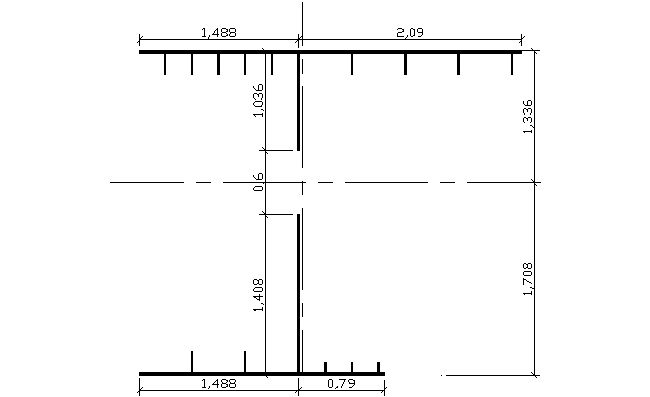
Otwory włazowe przyjęto o wymiarach 600x600 na wysokości 1,25m nad chodnikiem

W odległości co 15m wzdłuż dźwigara po obu stronach przekroju skrzynkowego.

---------------- REGIONS ----------------

Area: 0.2121

Perimeter: 21.6200

Bounding box: X: -1.5247 -- 2.0533

Y: -1.8087 -- 1.2353

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia: X: 0.3902

Y: 0.1541

Product of inertia: XY: 0.0675

Radii of gyration: X: 1.3565

Y: 0.8524

Principal moments and X-Y directions about centroid:

I: 0.1362 along [0.2567 0.9665]

J: 0.4081 along [-0.9665 0.2567]

Wx = Jx/z = 0,3902m⁴/1,708m = 0,22845m³

σ = M_max/Wx = 44,085 MNm/0,22845m³ = 192,97 Mpa > R = 195 MPa

Warunek spełniony

6.2.9.Max siła tnąca

Linia wpływu siły tnącej przy podporze

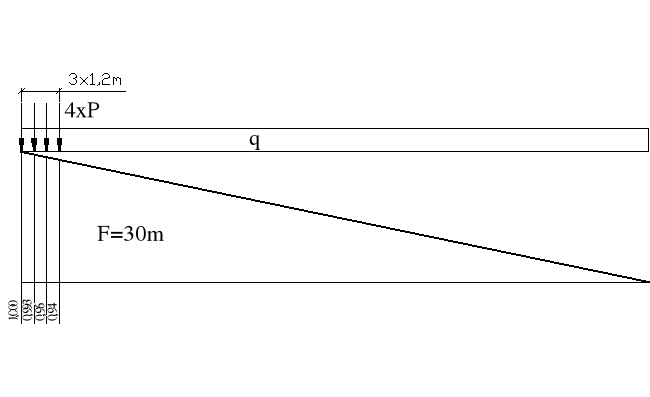
T_max = q*F+P* = 77,025 kN/m*30m+172,29 kN*(1+0,993+0,96+0,94)= 2981,47 kN

6.2.10.Sprawdzenie naprężeń stycznych w środniku

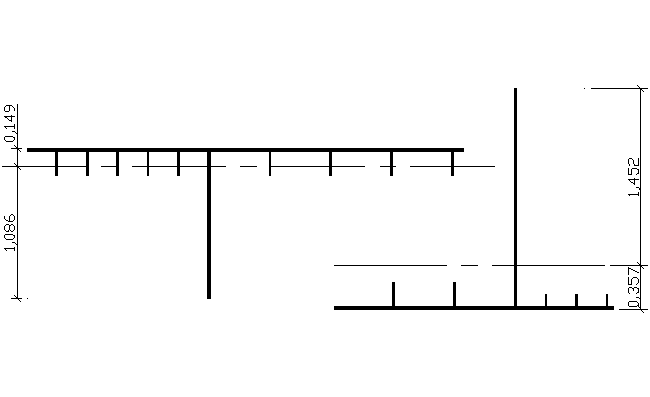
A = 0,1282m² A = 0,0959m²

Sxg = 0,1282m²*1,086m = 0,13923m³

Sxd = 0,0959m²*1,452m = 0,13925m³

 = T_max*S₁/(Jx*t_ś)=2981,47kN*0,13925m³/(0,3902m⁴*0,02m)= 53,2 Mpa < R_t = 115 Mpa

Warunek spełniony

6.2.11.Sprawdzenie ugięć dźwigara

f_max = 5,5M_maxL²/[48EJx] =

5,5*44,085 MNm*60²m²/[48*206000MPa*0,391m⁴] = 0,193m < f_dop=L/300= 0,2m

warunek spełniony

6.2.12.Sprwdzenie stateczności lokalnej środnika przy ścinaniu

b = 3m t = 0,02m

 = b/t = 3/0,02 = 150

e = 2m

 = e/b = 2m/3m = 0,667 < 1 => 1/ = 1,5 =>  = e/t = 2m/0,02m = 100 => K_t = 1660

_p = K_t/(R)^1/2 = 118,875

/_p = 100/118,875 = 0,841 => interpolacja m_st = 1,111

 = 53,2 MPa < R_t/m_st = 115/1,111 = 103,51 MPa

Warunek spełniony

6.2.13.Sprawdzenie żeber nad podporą

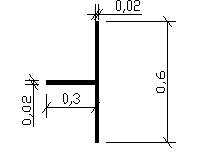
---------------- REGIONS ----------------

Area: 0.0180

Perimeter: 1.8400

Bounding box: X: -0.2566 -- 0.0634

Y: -0.3000 -- 0.3000

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia:X: 0.00036

Y: 0.0001

Product of inertia:XY: 0.0000

Radii of gyration: X: 0.1415

Y: 0.0906

Principal moments and X-Y directions about centroid:

I: 0.00010 along [0.0000 -1.0000]

J: 0.00036 along [1.0000 0.0000]

l_w= 3m , i_x = (Jx / A)^1/2 = (0,00036m⁴/0,018m²)^1/2 = 0,141m

=l_w/i_x = 3m/0,141m = 21,28

_p= 118(200/R)^1/2 = 118(200/195)^1/2 = 119,5

 _p = 21,28/119,5 = 0,178 => interpolacja m_w = 1,043

T_max = 2981,47kN

F_ż = 0,024m²

σ_c = T_max*m_w/F_ż = 2981,47kN *1,043 / 0,018m² = 172,76 MPa < R = 195 MPa

Warunek spełniony

6.2.14.Sprawdzenie nośności spoin pionowych żeber

T_max = 2981,47kN

_II = T_max/al. < sR => a > T_max/(sR*l ) = 2,98147MN / (0,8*195MPa*2*2,9m)

= 0,0033m

przyjęto spoinę pachwinową na wysokości środnika 2,9m o a = 4mm

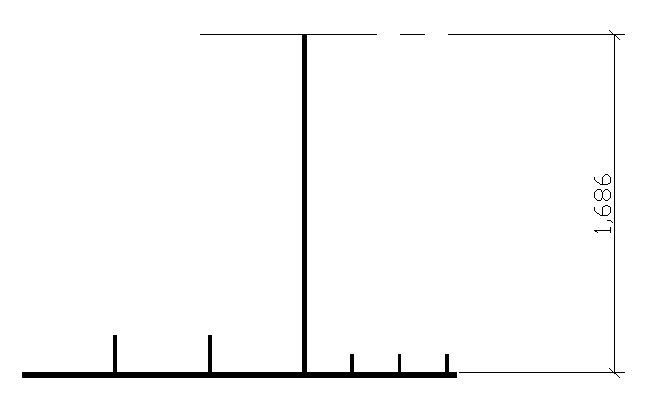
6.2.15.Przyjęcie spoin łączących pasy ze środnikiem

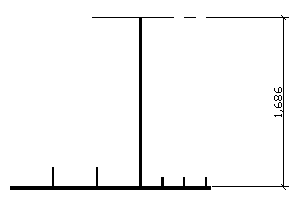
Sx = 0,05012m²*1,686m = 0,0845m

 = T_max*Sx/(Jx*2*a) < R_t => a > T_max*Sx/(Jx*2* R_t)

a > 2,98147MN *0,0845m³/(0,3902m⁴*2*115MPa)

a > 0,0028m

Przyjęto spoinę pasa dolnego i górnego o a = 4 mm

6.2.16.Sprawdzenie spoin czołowych montażowych środnika

Nie łączyć w środku rozpiętości (w odległości 7,5m od środka)

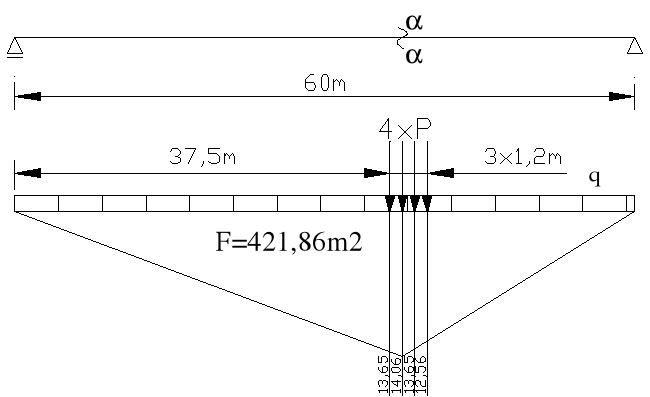
M_max = 77,025kN/m*421,86m²+172,29kN*(14,06+2*13,65+12,56)m = 41,784 MNm

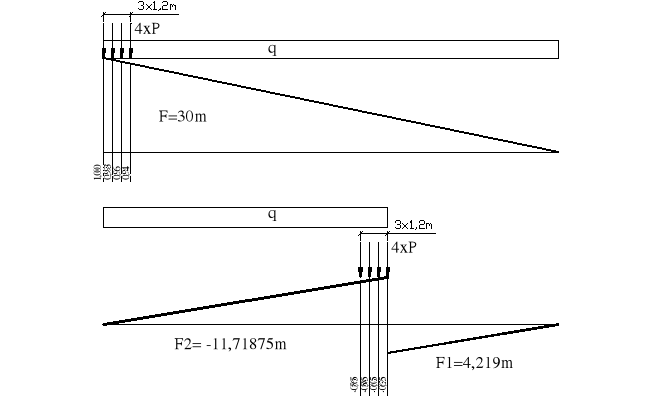
T = q*F2+P*(0,565+0,585+0,605+0,625) = 77,025kN/m*11,71875+172,29kN*2,38 =

1312,63 kN

wymiary środnika

h = 3m , t = 0,02m , A = 0,06m²

charakterystyki

Jx = 0,391m⁴

z = 1,708m => Wx = Jx/z = 0,391m⁴/1,708m = 0,229m³

σ = M_max/Wx = 41,784 MNm/0,229m³ = 182,46 MPa < R = 195MPa

 = T/A = 1,313 MN/0,06m² = 21,88 Mpa

σ_z = [(σ/s )²+3*²]^1/2=[(182,46/0,85)²+3*21,88²]^1/2=210,76 Mpa < 1,1R=1,1*195=214,5 MPa

Warunek spełniony

Przyjęto spoinę czołową w V o g = 20 mm

6.2.17. Sprawdzenie lokalnej stateczności ściskanej blachy

dźwigara

rozstaw poprzecznic 2m

rozstaw podłużnic 0,5m

szerokość współpracująca 0,281m

pole przekroju 0,009m²

naprężenia w dźwigarze σ_c = M_max/Wx_g = 44,085MNm*1,336m/0,3902m⁴= 150,94MPa

siła ściskająca F = A* σ_c = 1355,74kN

l_w = 2m , iż = [Jx/A]^1/2 = [0,334*10^-4m⁴/0,009m²]^1/2= 0,061m

 = l_w/iż = 2m/0,061m = 32,8

_p = 118[200/R]^1/2 = 119,5  _p = 32,8/119,5 = 0,274 => m_w = 1,08

σ = F*m_w/A = 1355,74kN*1,08/0,009m² = 162,7Mpa < R = 195Mpa

7.Chodnik służbowy

7.1.Zebranie obciążeń

• obciążenie tłumem

q_tO = 1,5kN/m²*1,3 = 1,95 kN/m²

• nawierzchnia betonowa

max q_bO = 20kN/m³*0,15m*1,5 = 4,5 kN/m²

min q_bO = 20kN/m³*0,15m*0,9 = 2,7 kN/m²

• izolacja

max q_iO = 14kN/m³*0,01m*1,5 = 0,21 kN/m²

min q_iO = 14kN/m³*0,01m*0,9 = 0,126 kN/m²

• poręcz

max q_pO = 6 kN/m

min q_pO = 3,6 kN/m

q_Omax = 1,95+4,5+0,21 = 6,66kN/m²

q_Omin = 2,7+0,126 = 2,826kN/m²

ciężar własny wspornika

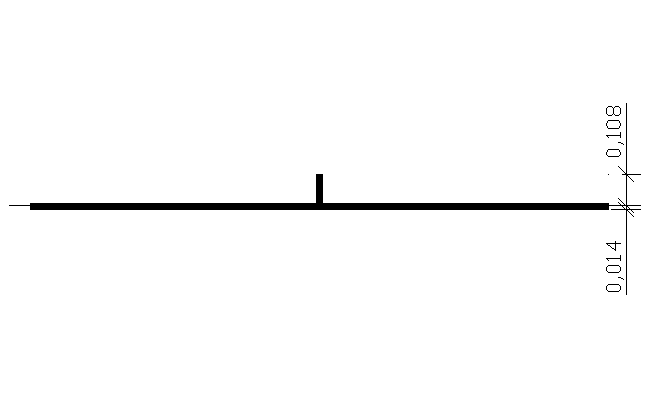
---------------- REGIONS ----------------

Area: 0.0460

max q_wO = 78,5kN/m³*0,046m²*1,2 = 4,33 kN/m

min q_wO = 78,5kN/m³*0,046m²*0,9 = 3,25 kN/m

7.2.Szerokość współpracująca blachy

Przyjęcie długości współpracującej płyty

b/L = 2 m/60m = 0,03

F_z/bg = 0,002m²/(2m*0,022m) = 0,046

odczytano poprzez interpolacje  = 0,88

b₀ = b *  = 2m * 0,88= 1,76m

przekrój skorygowany

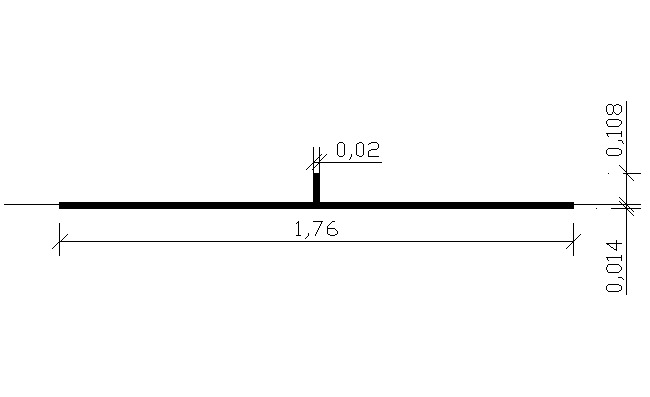
---------------- REGIONS ----------------

Area: 0.0407

Perimeter: 3.7640

Bounding box: X: -0.8800 -- 0.8800

Y: -0.0139 -- 0.1081

Centroid: X: 0.103*10^-4

Y: 0.0000

Moments of inertia:X: 0.0000

Y: 0.0100

Product of inertia:XY: 0.0000

Radii of gyration: X: 0.0159

Y: 0.4954

Principal moments and X-Y directions about centroid:

I: 0.0000 along [1.0000 0.0000]

J: 0.0100 along [0.0000 1.0000]

7.3.Linia wpływu reakcji na wsporniku do zebrania obciążenia

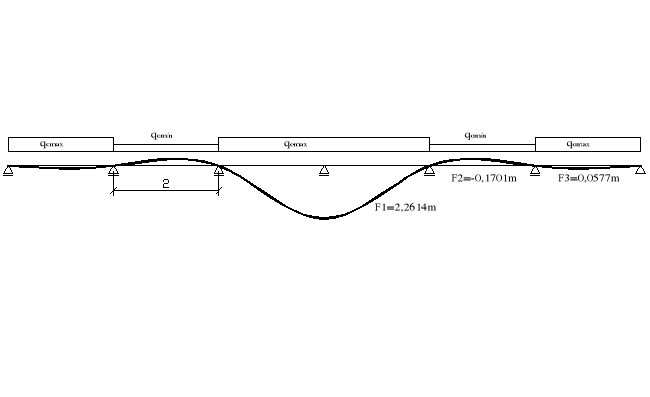
q = q_Omax*(F1+2*F3) - q_Omin*2*F2 + max q_wO = 6,66kN/m²*(2,2614+2*0,0577)m-

2,826kN/m²*2*0,1701m + 4,33 kN/m = 19,198 kN/m

Pp = max q_pO*(F1+2*F3)-min q_pO*2*F2 = 6kN/m*(2,2614+2*0,0577)m -

3,6kN/m*2*0,1701m = 13,036 kN

7.4.Moment wspornikowy chodnika

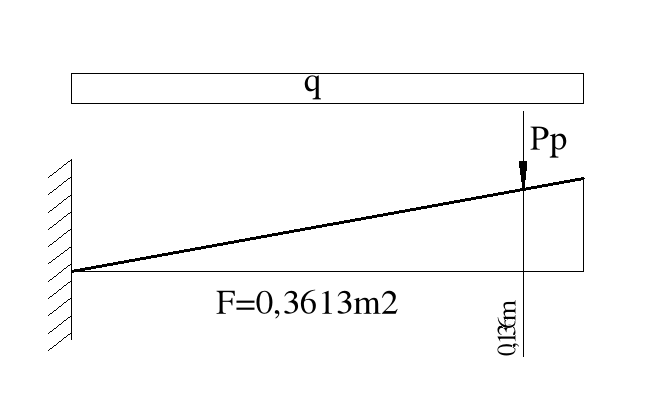
M_max= q*F+Pp*0,136m = 19,198kN/m*0,3613m²+13,036kN*0,136m = 8,709 kNm

7.5.Siła tnąca wspornika

T_max = q*0,85m+Pp = 19,198kN/m*0,85m+13,036kN = 29,354 kN

7.6.Sprawdzenie naprężeń

7.6.1.Naprężenia normalne

Wx = Jx/z = 0,0103*10^-3m⁴/0,108m = 0,0954*10^-3m³

σ = M_max/Wx = 8,709kNm/0,0954*10^-3m³ = 91,29 MPa < R = 195 MPa

warunek spełniony

7.6.2.Naprężenia styczne

 = T_max/(t_ś*h) = 29,354 kN/(0,02m*0,1m) = 14,68 Mpa < R_t = 115 MPa

warunek spełniony

7.6.3.Naprężenia w złożonym stanie naprężenia

σ_z = [σ²+3*²]^1/2 = [91,29MPa²+3*14,68MPa²]^1/2 = 94,76 MPa < R = 195 MPa

warunek spełniony

7.7.Przyjęcie spoin łączących pas ze środnikiem

Sx = 1,76m*0,022m*0,003m = 0,00012m³

_II = T_max*Sx/(Jx*2*a) < R_t => a > T_max*Sx/(Jx*2*R_t) = 14,68kN*0,00012m³/

( 0,0103*10^-3m⁴*2*115000kPa) = 0,00074m

przyjęto spoinę o a = 4mm

7.8.Sprawdzenie spoiny pachwinowej utwierdzenia wspornika

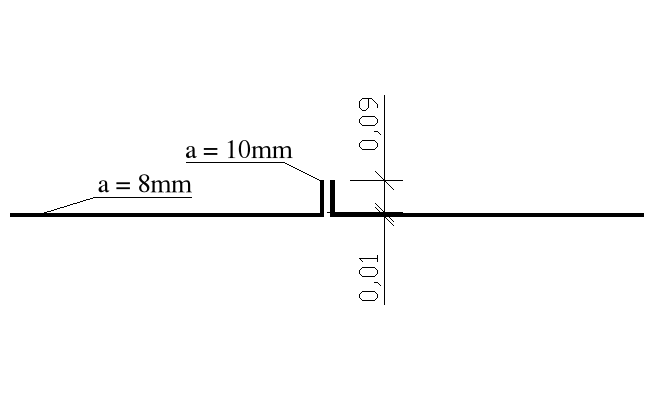
---------------- REGIONS ----------------

Area: 0.0158

Perimeter: 3.8800

Bounding box: X: -0.8800 -- 0.8800

Y: -0.0098 -- 0.0902

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia:X: 0.4794*10^-5

Y: 0.0036

Product of inertia:XY: 0.0000

Radii of gyration: X: 0.0186

Y: 0.4803

Principal moments and X-Y directions about centroid:

I: 0.0000 along [1.0000 0.0000]

J: 0.0036 along [0.0000 1.0000]

σ = My/Jx = 8,709kNm*0,09m/0,4794*10^-5m⁴ = 163,5 Mpa

 = T/al = 14,68kN /(2*0,01m*0,092m) = 7,98 Mpa

σ_z = [(σs)²+3* ²]^1/2 = [(163,5/0,8)²+3*7,98²]^1/2= 204,84 Mpa < 1,1R=1,1*195 = 214,5Mpa

warunek spełniony

7.9.Sprawdzenie podłużnic na wsporniku

7.9.1.Zestawienie obciążeń

• ciężar własny

charakterystyczny

q_PK = 78,5kN/m³*0,012m² = 0,942kN/m

obliczeniowy

max q_PO = q_PK*1,5 = 1,413kN/m

min q_PO = q_PK*0,9 = 0,848kN/m

• obciążenie tłumem

q_tO = 1,5kN/m²*1,3 = 1,95 kN/m²

• nawierzchnia betonowa

max q_bO = 20kN/m³*0,15m*1,5 = 4,5 kN/m²

min q_bO = 20kN/m³*0,15m*0,9 = 2,7 kN/m²

• izolacja

max q_iO = 14kN/m³*0,01m*1,5 = 0,21 kN/m²

min q_iO = 14kN/m³*0,01m*0,9 = 0,126 kN/m²

q_Omax = 1,95+4,5+0,21 = 6,66kN/m²

q_Omin = 2,7+0,126 = 2,826kN/m²

7.9.2.Zebranie obciążeń poprzez linie wpływu reakcji

podporowej podłużnicy

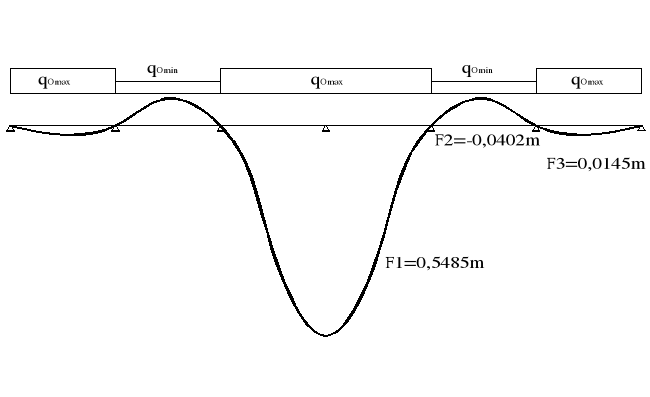
q_max = q_Omax (F1+2F3) - q_Omin *2*F2 + max q_PO = 6,66kN/m²*(0,5485+2*0,0145)m -

2,826kN/m²*2*0,0402m + 1,413kN/m = 5,032kN/m

q_min = q_Omin (F1+2F3) - q_Omax *2*F2 + min q_PO = 2,826kN/m²*(0,5485+2*0,0145)m -

6,66kN/m²*2*0,0402m + 0,848kN/m = 1,945 kN/m

7.10.Momenty max

moment przęsłowy

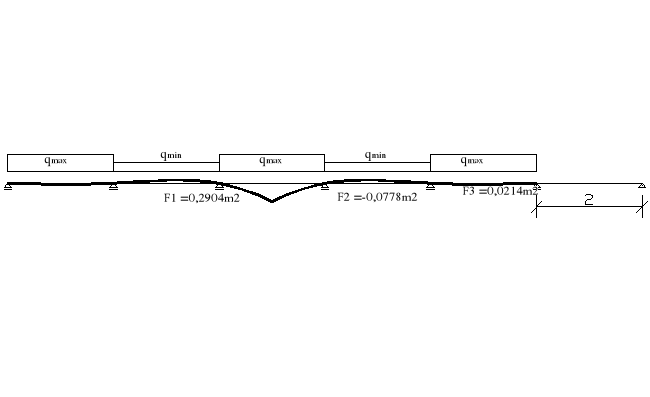
M_max = q_max*(F1+2F3) - q_min*2*F2 = 5,032kN/m*(0,2904+2*0,0214)m² -

1,945kN/m*2*0,0778m² = 1,374 kNm

moment podporowy

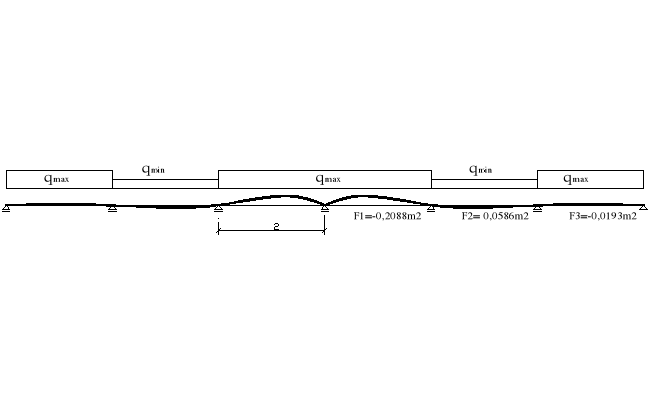
M_max= - q_max*(2F1+2F3) + q_min*2*F2 = - 5,032kN/m (2*0,2088 + 2*0,0193)m²+1,945kN/m*

2*0,0586m² = -2,068kNm

7.11.Sprawdzenie naprężeń normalnych

7.11.1.Wyznaczenie szerokości współpracującej płyty

b/L = 0,5 m/2m = 0,25

F_z/bg = 0,002m²/(0,5m*0,022m) = 0,18

odczytano poprzez interpolacje  = 0,435

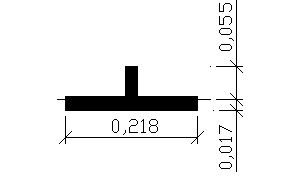
b₀ = b *  = 0,5m * 0,435 = 0,218m

przekrój skorygowany

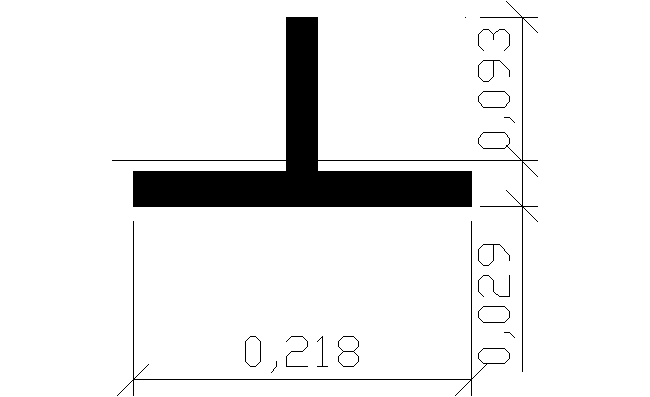
---------------- REGIONS ----------------

Area: 0.0068

Perimeter: 0.6800

Bounding box: X: -0.1090 -- 0.1090

Y: -0.0289 -- 0.0931

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia:X: 0.7112*10^-5

Y: 0.0000

Product of inertia:XY: 0.0000

Radii of gyration: X: 0.0323

Y: 0.0530

Principal moments and X-Y directions about centroid:

I: 0.0000 along [1.0000 0.0000]

J: 0.0000 along [0.0000 1.0000]

Wx = Jx/z = 0,7112*10^-5m⁴/0,093m = 7,648*10^-5m³

Na moment przęsłowy

σ = M_max/Wx = 1,374 kNm/7,648*10^-5m³= 17,965 Mpa > R = 195 MPa

Na moment podporowy

σ = M_max/Wx = 2,068 kNm/7,648*10^-5m³= 27,04 Mpa > R = 195 MPa

Przekrój niewykorzystany - zmiana przekroju

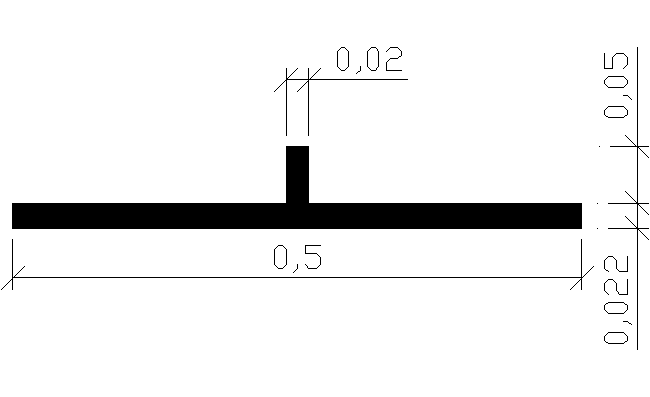
szerokość współpracująca płyty

b/L = 0,5 m/2m = 0,25

F_z/bg = 0,001m²/(0,5m*0,022m) = 0,091

odczytano poprzez interpolacje  = 0,435

b₀ = b *  = 0,5m * 0,435 = 0,218m

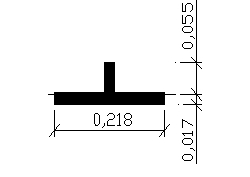
---------------- REGIONS ----------------

Area: 0.0058

Perimeter: 0.5800

Bounding box: X: -0.1090 -- 0.1090

Y: -0.0172 -- 0.0548

Centroid: X: 0.0000

Y: 0.0000

Moments of inertia X: 0.147*10^-5

Y: 0.0000

Product of inertia: XY: 0.0000

Radii of gyration: X: 0.0159

Y: 0.0573

Principal moments and X-Y directions about centroid:

I: 0.0000 along [1.0000 0.0000]

J: 0.0000 along [0.0000 1.0000]

Wx = Jx/z = 0,147*10^-5m⁴/0,055m= 2,672*10^-5m³

Sprawdzenie naprężeń normalnych w przekroju zmienionym , skorygowanym

Na moment przęsłowy

σ = M_max/Wx = 1,374 kNm/2,672*10^-5m³= 51,42 Mpa > R = 195 MPa

Na moment podporowy

σ = M_max/Wx = 2,068 kNm/2,672*10^-5m³= 77,4 Mpa > R = 195 MPa

warunki spełnione

7.12.Max siła tnąca

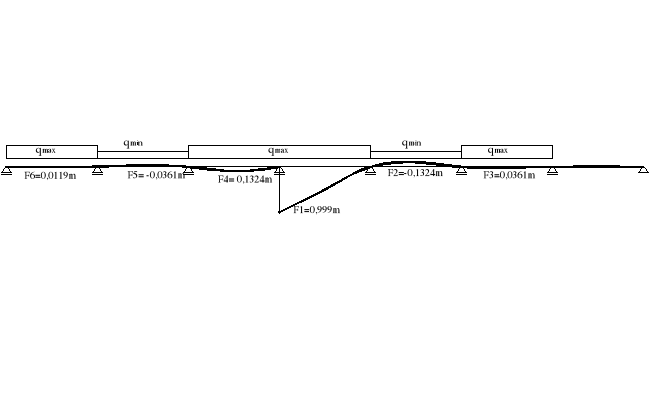
T_max = q_max*(F1+F4+F3+F6) - q_min* (F2+F5) = 5,032kN/m*(0,999+0,1324+0,036+0,0119)m

- 1,945kN/m*(0,1325+0,036)m = 5,607 kN

7.13.sprawdzenie naprężeń stycznych

t_ś = 0,02m

h = 0,05m

 = T_max/t_śh = 5,607kN/(0,05m*0,02m) = 5,6 Mpa < R_t = 115MPa

warunek spełniony

7.14.Przyjęcie spoin pachwinowych łączących pas ze środnikiem

Sx = 0,022m*0,218m*(0,022m-0,017m) = 0,24*10^-4m³

Jx = 0,147*10^-5m⁴

 = T_max*Sx/Jx*2*a < R_t => a > T_max*Sx/Jx*2*R_t = 5,607kN*0,24*10^-4m³/(0,147*10^-5m⁴*

2*115Mpa) = 0,0004m

Przyjęto spoinę o a = 4 mm

7.15.Prztjęcie spoin łączących podłużnice ze wspornikiem

moment podporowy M_max = 2,068kNm

siła tnąca przy podporze T_max = 5,607 kN

Przyjęcie spoin o a = 8mm

Wx = 0,134*10^-4m³

Jx = 0,335*10^-6m⁴

Sx = 0,1*10^-4m³

σ = M_max/Wx = 2,068 kNm/0,134*10^-4m³ = 154,33 MPa < sR = 156 MPa

=T_max*Sx/Jx*4*a=5,607kN*0,1*10^-4m³/(0,335*10^-6m⁴*4*0,008m)=5,23Mpa < R_t= 115MPa

naprężenia w złożonym stanie naprężenia

σ_z = [(σ/s )²+3*²]^1/2=[(154,33/0,8)²+3*5,23²]^1/2 = 193,12MPa < 1,1R = 214,5MPa

warunek spełniony

7.16.Przyjęcie spoin montażowych podłużnic

podłużnice należy spawać w przęśle

M_max = 1,374kNm

Wx = 0,834*10^-5m³

σ = M_max/Wx = 1,374kNm/0,834*10^-5m³ = 164,74MPa < sR = 0,85*195 = 165,7Mpa

warunek spełniony

przyjęto spoinę czołową a = 20mm o wysokości h = 0,05m

7.17.Sprawdzenie lokalnej stateczności podłużnic

podłużnice zabezpieczone przed zwichrzeniem przez obetonowanie

8.Dobranie łożysk

Nośność łożysk odpowiada sile reakcji podporowej na dźwigarze skrajnym od obciążeń charakterystycznych.

Korekta obciążenia dźwigara skrajnego patrz pkt.6.2.1..

q = q_dk*F1+ q_ka*F4+q_t*F5+Q_k*0,8335+ q_g*1,33+ q_p*1,294+ q_b*0,9271+

q_hk*F6 + q_b* 0,9441- q_hk*F7 - q_b *0,2781 - q_od*F2 - q_ka*F3

-q_b*0,2611 -q_p*0,6286 -q_g*0,6645 =

6,646 kN/m²*2,4291m+4,893kN/m²* 3,6339m+2,5kN/m²*2,7568m+21,015kN/m

*0,8335 + 2kN/m*1,33+4kN/m*(1,294+0,9271) + 3kN/m²*0,7601m+4kN/m*0,9441

- 3kN/m²*0,194m - 4kN/m * 0,2781- 2,646kN/m*0,0981 - 4,893kN/m*

1,3829 - 4kN/m*(0,2611+0,6286) - 2kN/m*0,6645 = 62,326 kN/m

P_c = K_k/8 = 840kN/8 = 105kN

P = P_c*(0,3539+0,74) = 105kN*1,0939 = 114,86 kN

Linia wpływu reakcji podporowej dla dźwigara skrajnego

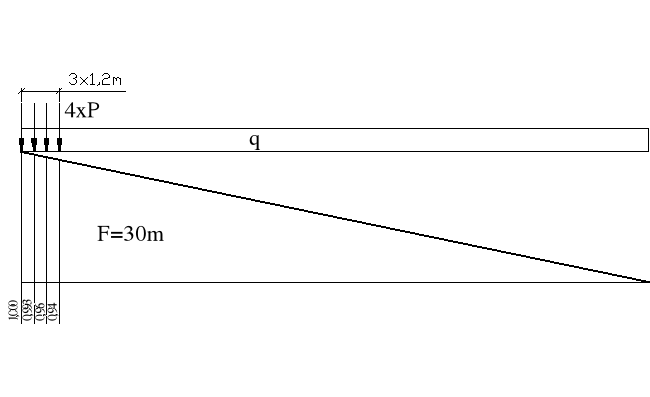
R = q*F + P* = 62,326kN/m*30m + 114,86kN*(1+0,993+0,96+0,94) = 2316,93kN

Przyjęto gotowe łożyska z katalogu :

są to łożyska soczewkowe produkowane przez firmę PRInż-ZPM

Dane przyjętych łożysk :

Nośność - 3000kN

Wysokość konstr. - 120mm

Wymiary kwadratu

płyty dolnej - 460mm

Wymiary

płyty górnej - 520x670mm

Masa : Możliwe przemieszczenia : e_x[mm] e_y[mm]

stałe - 250k - 0 - 0

jedno przesuwne - 310kg - +-100 - 0

wielo przesuwne - 240kg - +-100 - +-20

Naprężenia dopuszczalne na beton pod łożyskiem σ_dop = 20MPa

Dopuszczalny kąt obrotu [tg_dop = 0,01

Układ przyjętych łożysk

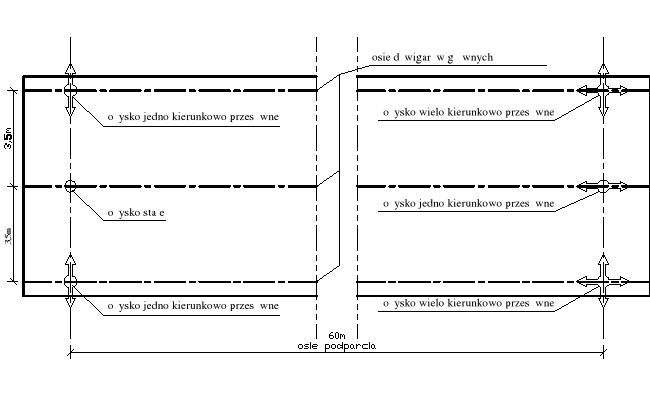
• sprawdzenie nośności łożysk

R = 2316,93kN < N = 3000kN

• sprawdzenie naprężeń w betonie pod łożyskiem

Pole płyty dolnej łożysk F = 0,46²m² = 0,2116m²

σ_b = R/F = 2,31693kN/0,2116m² = 10,95 MPa < σ_dop = 20MPa

• sprawdzenie kąta obrotu konstrukcji przy podporze dla max ugięcia dopuszczalnego

tg = f_dop/[L/2] = 0,2m/30m = 0,0066 < [tg_dop = 0,01

Budowa łożysk :

Łożyska soczewkowe wykonane są ze stali w postaci wklęsłych czasz cylindrycznych , w których osadzone są wypukle - płaskie soczewki o polerowanej części wypukłej , mające możliwość obrotu dzięki umieszczeniu w tych czaszach warstwy PTFE (tarflenu).

Przemieszczenia poziome zapewnia płyta górna powleczona blachą austenityczną ,ślizgająca się po warstwie PTFE umieszczonej na płaskiej powierzchni soczewki .

Łożysko soczewkowe umożliwia obrót konstrukcji wokół dowolnej osi (obrót punktowy).

Przesuwy realizowane są pomiędzy poszczególnymi płytami łożyska .Poprzez zastosowanie prowadnic , trzpienia lub pierścienia ograniczającego przesuw z łożyska wielokierunkowo przesuwnego otrzymujemy łożysko jednokierunkowo przesuwne lub stałe .

W celu podniesienia nośności arkusze PTFE w łożysku zostały wpuszczone w stal na około pół ich grubości (2mm).

---