Tematy przedegzaminacyjne z „SYSTEMY I STEROWANIE".

dla studentów WE, Automatyka i Technika Mikroprocesorowa, s. VIII

(Pytania w trakcie egzaminu mogą mieć charakter zbliżony do niżej wymienionych.)

1. Jaką postać przyjmuje model zmiennych stanu dla liniowego, stacjonarnego obiektu dynamiczne­go? Podaj przykład równań stanu dla obiektu nieliniowego i dla niestacjonarnego obiektu drugie­go rzędu.

Linowy, stacjonarny model opisany jest równaniami różniczkowymi, liniowymi. Model zmiennych stanu przyjmuje standardową postać:
, przy czym:

A-macierz stanu n/n m- liczba wejść

B- macierz wejść n/m p- liczba wyjść

C- macierz wyjść p/n n- rząd zmiennych stanu, równy rzęd.

D- macierz transmisyjna p/m

Przykład równań stanu dla obiektu nieliniowego i niestacjonarnego:

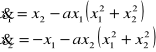
Obiekt niestacjonarny będzie się charakteryzował czasem t przy każdej ze zmiennych stanu

2. W jaki sposób macierz stanu, np. w postaci A=[-1.0 0.4; 0.1 -2] można sprowadzić do postaci modalnej? Jakie są wektory i wartości własne a także wielomian charakterystyczny tej macierzy?

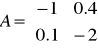
Liczymy wyznacznik macierzy:

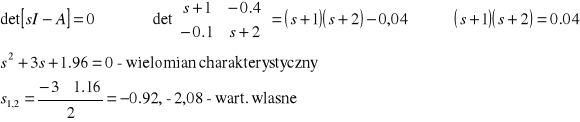
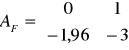
- macierz Frobeniusa w postaci modalnej reprezentuje macierz

zmiennych stanu fazowych. Jeżeli: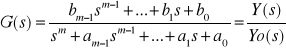
, to

,

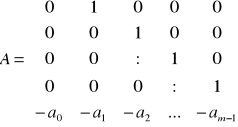
3. W jaki sposób możemy przekształcić zmienne stanu układu dynamicznego do postaci fazowej? Wypowiedź należy zilustrować przekształceniem dla układu dx/dt = Ax; dla macierzy A z p.2.
   Zmienne stanu fazowe są obierane w ten sposób że: x₁'=x₂. W naszym przypadku, gdy x'=Ax mamy (z punktu powyżej):

wielomian charakterystyczny (mianownik transmitancji): s²+3s+1,96

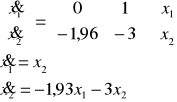
Równanie stanu w postaci modalnej

4. Wyznacz równania stanu dla (wielowymiarowego) układu dynamicznego o zadanej transmitancji i transmitancję układu dla zadanych równań stanu.
   Ogólnie:

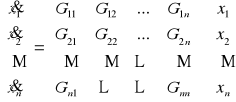
- po wymnożeniu otrzymamy równania:

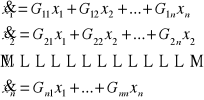
- równia stanu układu wielowymiarowego:

5. W jaki sposób, dysponując modelem analogowym zmiennych stanu liniowego i stacjonarnego obiektu dynamicznego, możemy uzyskać model dyskretny zmiennych stanu tegoż obiektu?

Poprzez transformatę Z:

;

6. Wymień przynajmniej dwie wersje zaleceń nt. wyboru czasu próbkowania w układzie regulacji.

Podstawowe zalecenie doboru czasu próbkowania wywodzi się z Twierdzenia Shonana - Kotielnikowa, w którym mowa jest o tym, iż sygnał analogowy powinien być próbkowany z częstotliwością co najmniej dwukrotnie większą od częstotliwości układu, aby możliwe było odtworzenie sygnału analogowego na podstawie spróbowanego.
Inne zalecenie: Czas regulacji układu ciągłego podzielony przez 10 jest dobrym czasem próbkowania. Przyjmuje się że zadawalającym czasem próbkowania jest: T_pr=t_r/10

Na podstawie doboru PID: T=(2 do 8)T_I

Na podstawie charakterystyki częstotliwościowej: T=2π/(10⋅ω_r)

7. Przedstaw główne związki między położeniem biegunów dyskretnego układu regulacji i jego wła­snościami. Gdzie leżą bieguny i jakie własności ma układ ze skończoną odpowiedzią impulsową?

Bieguny układy dyskretnego muszą być położone w kole jednostkowym na płaszczyźnie zmiennej zsespolonej. Tylko ten warunek zapewnia stabilność układowi. Na dokładniejsze umiejscowienie biegunów układu dyskretnego ma wpływ jego przeznaczenie oraz sterowanie którym dysponujemy (możemy bowiem dysponować tylko niewielkim zakresem sterowań). Umieszczanie biegunów bliżej środka układu płaszczyzny zmiennej zespolonej (przy założeniu, że pierwiastki są rzeczywiste) osiągamy iż układ staje się o wiele gwałtowniejszy, a czas ustalania odpowiedzi krótszy. Potrzebna jest jednak większa wartość sterowania.
Natomiast, przy zbliżaniu się do 1 układ jest co raz wolniejszy, a nawet nie osiąga stanu ustalonego, lecz stosujemy przy tym mniejszy wydatek energii na sterowanie.
Dobieranie biegunów zespolonych sprzężonych ma pozytywny wpływ na układ szczególnie w przypadku, gdy linie pierwiastkowe zostaną nachylone względem osi Re pod kątem 45⁰. Wtedy układ ma optymalną wartość tłumienności 0.707, co sprawia iż przeregulowania w układzie są znikome, czas regulacji krótki a potrzeba sterowania stosunkowo niewielka.

Bieguny układu o skończonej odpowiedzi impulsowej (SOI) leżą w środku układu współrzędnych. Układ z taką lokacją biegunów charakteryzuje się najkrótszym minimalnym czasem osiągania stanu ustalonego. Wielomian charakterystyczny takiego obiektu ma postać: A(z)=z^n+d

8. Wyraź, za pośrednictwem równania stanu i równania wyjścia model stacjonarnego, liniowego obiektu SISO o podanym równaniu różniczkowym (różnicowym). Z założenia w modelu zastoso­wano fazowy układ zmiennych stanu.

Obiekt SISO - oznacza obiekt o pojedynczym wejściu i pojedynczym wyjściu

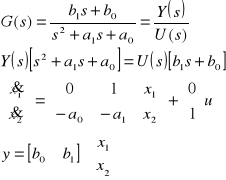
9. Przedstaw zwięźle znane sposoby projektowania sprzężenia korekcyjnego od zmiennych stanu. Jaki cel staramy się przy tym osiągnąć?

O Fuck. Nie mało tego. Bo sprzężenie korekcyjne od zmiennych stanu dotyczy wielu metod. Chodzi tu oto, że musimy wpłynąć na wybraną zmienną stanu, poprzez zastosowania sprzężenia zwrotnego od tych zmiennych. Wzmocnienie w tej linii sprzężenia jest wektorem kolumnowym.

Do metod wyznaczania macierzy sprzężenia możemy zaliczyć co najmniej 4:

1. Metoda analityczna
2. Metoda Ackerman'a
3. Metoda LQR
4. Metoda analityczna Brogana

Ad 1: (analityczna)

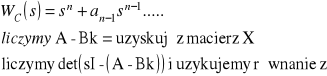
porównujemy „z” współczynniki ze współczynnikami W_c(s) i mamy k₁ k₂ itd
Ad 2: wzory Ackerman'a

Ad 4: (Brogana)

10. Przedstaw schemat układu regulacji od zmiennych stanu z obserwatorem Leunbergera eksponując strukturę obserwatora.

Rys 1

Równanie obserwatora Leunbergera:

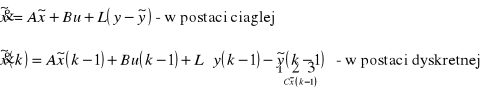
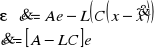
Wadą rozwiązania jest zwiększanie się rzędu układu n razy.

11. W jaki sposób projektuje się obserwator? Czy metody syntezy układu obserwatora zmiennych stanu i syntezy regulatora ze sprzężeniem od zmiennych stanu mają wspólne elementy?

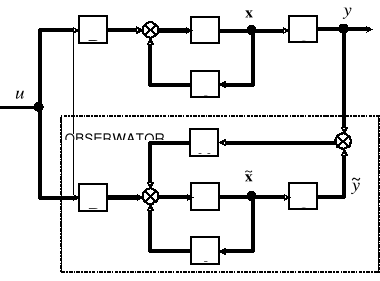
Pierwszą podstawową rzeczą jest sprawdzenie warunku obserwowalności układu:

rankO=n, gdzie O jest macierzą sterowalności o postaci: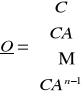

Jeżeli układ jest obserwowalny, przystępujemy do projektowania:

Równanie stanu obserwatora:

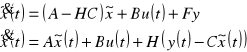
Równanie to jest równaniem obserwatora pełnego rzędu. Macierz H

wyznaczymy stosują wzory Ackermana: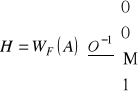

W_F powstaje w wyniku podstawienia macierzy A za zmienną s równania charakterystycznego:

Cechy wspólne: Możemy dokonywać sterowania przy użyciu obserwatora, ponieważ obserwator odtwarza zmienne stanu rozpatrywanego układu. Na ich podstawie możemy zastosować sprzężenie, które będzie regulowało układ. Możemy przy tym korzystać np. z metody Ackermana.

12. Przedstaw metodę syntezy regulatora i obserwatora w układzie sterowania związaną z zastosowa­niem wzorów Ackermana.

Synteza regulatora:

Dzięki metodzie Ackermana możemy wyznaczyć macierz sprzężeń zwrotnych od zmiennych stanu. Jest to więc regulator modalny.

u=-Kx

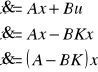
Problem syntezy regulatora sprowadza się do wyznaczenia współczynników wzmocnień macierzy K. Stosujemy tu więc metodę Acekrmana:

Synteza obserwatora:

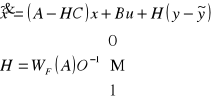
Obserwator pełni rolę swoistego filtru dolnoprzepustowego. Przebiegi y oraz estymatora y mogą się od siebie nieznacznie różnić. Jest to wynikiem zakłóceń działających przed integratorem, których obserwator nie może uwzględniać. Po to właśnie została wprowadzona do układu informacja w postaci uchybu dwóch sygnałów wyjściowych (Luneberger). Jest to swoista kontrola porównawcza sygnałów która minimalizuje czynnik błędu (uchyb).

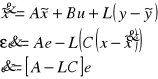
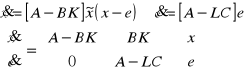
13. Podaj twierdzenie Lapunowa nt. stabilności układów dynamicznych.

Układa nieliniowy opisany równaniem
jest stabilny asymptotycznie w obszarze D, zawierającym początek układu współrzędnych (punkt równowagi x_r=0), jeżeli można dobrać funkcję Lapunowa V(x), dodatnio określoną w obszarze D, której pochodna względem czasu V'(x) wzdłuż trajektorii stanu jest funkcją ujemnie określoną w tym obszarze D. Jeżeli pochodna V'(x) jest funkcją ujemnie półokreśloną w obszarze D, to układ jest stabilny w tym obszarze D, ale niekoniecznie asymptotycznie stabilny.

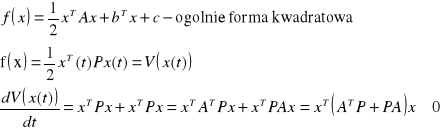
14. Jaką funkcję nazywamy funkcją Lapunowa? W jaki sposób można zastosować ideę funkcji Lapu­nowa przy konstrukcji reguły sterowania?

Funkcją lapunowa nazywamy funkcję która jest:

• funkcja ta jest dodatnio określona w obszarze D: V(x)>0 dla x≠0 i V(0)=0.

• wartość funkcji V(x) rośnie do nieskończoności, jeżeli długość wektora x dąży do nieskończoności, tzn, V(x)→∞ jeżeli ||x||→∞.

• pochodna względem czasu t jest ujemnie określona w obszarze D (V'(x)<0 dla x≠0 i V(o)=0 tylko dla x=0) lub jest ujemnie półokreślona w tym obszarze.

Sposób wykorzystania idei funkcji: Przykładem funkcji Lapunowa jest forma kwadratowa. Praktycznie każdą dowolną funkcję możemy przybliżyć formą kwadratową. W związku z tym mając już funkcję Lapunowa, możemy znaleźć trajektorię dowolnego układu, która zarazem zapewni nam stabilność układu.

Za pomocą funkcji Lapunowa możemy też dokonywać sterowania i regulacji układu nieliniowego.

15. Przedstaw ogólną postać równania regulatora dyskretnego, a następnie posługując się tymi samy­mi wielkościami (w(k), y(k), u(k) ), równanie dyskretnego, przyrostowego regulatora PID.

Równanie regulatora dyskretnego:

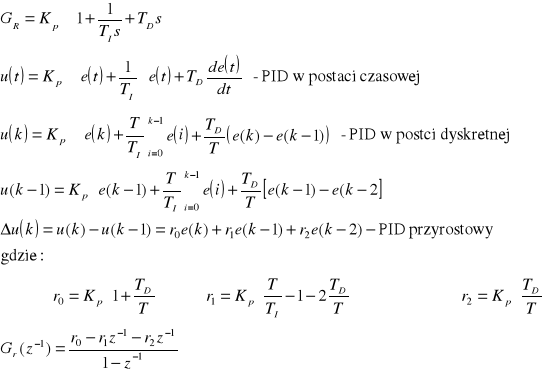
16. Przedstaw typowy schemat układu regulacji z regulatorem cyfrowym typu PPC. W jaki sposób wyraża się transmitancja tego układu? Jakie wielomianowe równanie diofantyczne obowiązuje dla układu sterowania z regulatorem PPC? Czy rozwiązanie tego równania jest jednoznaczne?

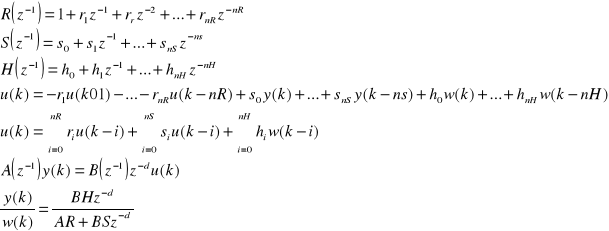
Równanie diofantyczne dla PPC:

to nie wszystko!!

17. Jakie (ogólnie rzecz ujmując) umiejscowienie biegunów układu regulacji jest szczególnie ko­rzystne? Dlaczego? Gdzie znajdują się zera układu sterowania z regulatorem PPC?
    patrz ad 7.

18. Co nazywamy zbiorem wypukłym i funkcją wypukłą - podaj definicje. W jakiej sytuacji zadanie znalezienia ekstremum funkcji ma jednoznaczne rozwiązanie?

Zbiór A należący do przestrzeni R² jest wypukły wtedy gdy dla każdego x i y odcinek o końcach x i y zawiera się w A. Jeżeli potrafimy pokazać taki odcinek, którego końce należą do zbioru A, a on sam nie zawiera się w tym zbiorze, to A nie jest zbiorem wypukłym.

Funkcja jest wypukła, gdy nad nią (wypukła ku górze), lub pod nią (ku dołowi) znajduje się zbiór wypukły.

Zadanie wyznaczenia ekstremum funkcji ma na pewno jednoznacznie rozwiązanie w przypadku gdy funkcja jest kwadratowa, tzn. gdy nie posiada ekstremum lokalnego a jedynie jedno ekstremum - globalne.

19. Wymień dwie typowe postacie formułowania warunku zatrzymania obliczeń (tzw. warunek STO­PU) przy posługiwaniu się algorytmem iteracyjnym znalezienia ekstremum funkcji.

Na moją głowę to:

STOP jeśli znalazłeś ekstremu (czyli zmiany w przyroście funkcji są mniejsze niż założono w programie (sigma)), to zatrzymaj i zapisz rezultat:

STOP jeśli nie możesz znaleźć to zatrzymaj i wyświetl błąd

20. Przedstaw, wymieniając kolejne działania w punktach, wybrany iteracyjny algorytm optymalizacji funkcji jednej zmiennej w sytuacji deterministycznej i wybrany algorytm posługujący się zakłóco­nymi pomiarami tej funkcji. Jakie parametry należy ustalić przed startem danych algorytmów?

--> Algorytmy optymalizacji funkcji jednej zmiennej (w sytuacji deterministycznej)
Metody iteracyjne są podstawą konstrukcji algorytmów znajdowania ekstremum funkcji.

Podstawowa idea tych metod związana jest z określeniem tzw. Funkcji iteracyjnej wyznaczającej następną wartość argumentu badanej funkcji: u(k+1) na podstawie jego m uprzednich wartości: u(k), u(k-1), …, u(k-m+1) i wartości badanej funkcji: f(u) (a także czasami jej pochodnych) w tych punktach. Punkt startowy wybiera się na podstawie informacji dostępnej przed rozpoczęciem procesu poszukiwania.

Algorytm pochodnej wynika ze znanego faktu, że minimum (ciągłej i posiadającej ciągłą pochodną) funkcji wypukłej w dół znajduje się w punkcie zerowym tej pochodnej, tj. w takim punkcie u* w którym: df(u)/du|_u=u*=0. Typowa postać algorytmu pochodnej:

u(k+1)=u(k)-α(k)[df(u)/du]|_u(k), k=0,1,2,…

Warunkiem koniecznym zbieżności danego algorytmu do optymalnego u=u*, niezależnie od wyboru punktu początkowego u(0), jest wybór współczynników szeregu α(k) w postaci zapewniającej:

Algorytm ten ma tę właściwość, że w miarę zbliżania się x(k) do x*, wartość (df/dx)|_x(k) dąży do 0, a zatem poprawki są coraz mniejsze. Można zwiększyć szybkość zbieżności biorąc pod uwagę tylko znak pochodnej:

u(k+1)=u(k)-α(k)sign[df(u)/du]|_u(k), k=0,1,2,…

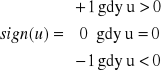
Dla zbieżności takiego algorytmu oprócz warunku
musi być spełniony warunek
gdyż w przeciwnym razie począwszy od pewnego K, tj. dla k>K, otrzymamy ciąg x(K), x(K+1), … oscylujący dookoła x*

Algorytm Newtona jest udoskonaloną wersją algorytmu pochodnej wymagającą jednak również znajomości drugiej ochodnej:

u(k+1)=u(k) - [d²f(u)/du²]|_u(k) [df(u)/du]|_u(k), k=0,1,2,…

Można wykazać, że jeżeli funkcja kryterialna jest kwadratową, tzn. typu: f(u)=au²+bu+c to działając zgodnie z algorytmem Newtona, minimum jej znajdujemy już po pierwszej iteracji. Znajomość odwrotności drugiej pochodnej pozwala wówczas ustalić jednoznacznie wartość współczynnika α.

Algorytm złotego podziału (algorytm związany z redukcja przedziału nieokreśloności) nazwę zawdzięcza charakterystycznej dla tej metody liczbie γ=(sqrt(5)-1)/2=0,618, wytyczającej zdaniem starożytnych Greków doskonałe proporcje kształtu prostokąta. Po jego przeanalizowaniu łatwo zauważyć, że szerokość badanego przedziału maleje proporcjonalnie do γ ^k=0,618 ^k.

Jeżeli:

Dla ciągłej funkcji f(x) w przedziale (a,b) posiadającej w tym przedziale jedno ekstremum (czyli unimodalnej) można je określić przez znalezienie z określoną dokładnością przedziału, w którym ono się znajduje. W tym celu należy obliczyć wartości funkcji w dwóch punktach wewnątrz tego przedziału, gdyż wyznaczenie tylko jednego nie wystarcza do stwierdzenia, w którym przedziale znajduje się szukane minimum. Po obliczeniu wartości funkcji w drugim punkcie można już jednoznacznie określić ten przedział - na rysunku odpowiednio przedziały (x₂,b) oraz (x₁,x₂). Ze względu na to, iż jeden z wcześniej wyliczonych punktów znajduje się zawsze wewnątrz nowego podprzedziału, w następnym kroku wystarczy już obliczyć wartość funkcji w jednym nowym punkcie.

[Author:TK]

algorytm posługujący się zakłóco­nymi pomiarami tej funkcji

Wyznaczenie optymalnych warunków realizacji procesu technologicznego wymaga (przy założeniu niestacjonarności lub nieznajomości postaci funkcji kryterialnej) przeprowadzenia określonego programu badań eksperymentalnych bezpośrednio na obiekcie. W programie tego rodzaju często nie odtwarza się pełnej postaci funkcji kryterialnej, a jedynie znajduje się jej ekstremum. Ściślej rzecz ujmując, z reguły w praktyce za zadawalające rozwiązanie zadania uważane jest znalezienie się w dostatecznie bliskim (z punktu widzenia celu optymalizacji) otoczeniu aktualnego położenia punktu ekstremalnego. W praktyce stosuje się „ostrożnie” (zwielokrotnienie pomiaru, wielkość kroku) wersje najprostszych metod deterministycznych.

Algorytm pochodnej może być stosowany oczywiście jedynie przy dostępności pomiarów pochodnej funkcji kryterialnej. W warunkach nieskorelowanych realizacji stacjonarnych zakłóceń stochastycznych pomiarów pochodnej zbieżność tego algorytmu w sensie średniokwadratowym, tj. z gwarancją:

E{u(k)-u*}→0 przy k→∞

Zapewnia odpowiedni dobór ciągu współczynników α(k). Zgodnie z twierdzeniem Robbinsa - Monro o aproksymacji stochastycznej szereg ten powinien spełniać warunki:

na przykład:
gdzie w ∈ [0,1]

Podkreślmy także, że skutkiem tego twierdzenia jest także zbieżność średniokwadratowa procedur opartych na uśrednianiu określonej liczby pomiarów pochodnej. Powtarzanie doświadczeń z uśrednieniem wyników prowadzi bowiem jedynie do zmniejszenia wariancji mierzonej wielkości:

Jeżeli: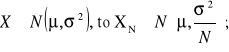

Przy zachowaniu innych warunków zbieżności algorytmu.

Tą samą uwagę można odnieść również w stosunku do zbieżności algorytmu opartego na znaku pochodnej.

21. Przedstaw (w punktach) sieć działań optymalizacji wg metody najszybszego spadku, wg kierun­ków sprzężonych, algorytm Newtona - Raphsona.

Metoda najszybszego spadku:

Przyjmijmy, że x(k) jest pewnym przybliżeniem punktu x* minimum funkcji f(x). Według algorytmu najszybszego spadku przejście z punktu x(k) do punktu x(k+1), będącego kolejnym przybliżeniem, jest określone zależnością:

Przy przejściu z punktu x(k) do x(k+1) jest wybierana taka wartość α_k, aby funkcja f(x) osiągała w punkcie x(k+1) minimum w kierunku
.

E1: określ kierunek poszukiwań
(prostopadły do stycznej do warstwicy)

E2: wyznacz minimum w tym kierunku

E3: zmień kierunek, wróć do E1 i powtarzaj aż osiągniesz minimum.

Metoda słaba przy funkcji w postaci wąskiej doliny.

Algorytm:

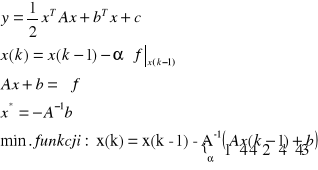
Jeżeli α=A to x(k-1)-x(k-1)-A^-1b=x^* Funkcja w jednym kroku znalazła ekstremum.

Musimy znać A a funkcja musi być formą kwadratową. Jest to metoda stosowania odpowiedniego współczynnika. Algorytm:

Metoda Kierunków sprzężonych

Niezależnie od wyboru punktu początkowego x(0) punkt minimum funkcji kwadratowej

½ x^TAx+b^Tx+c znajdziemy wykonując zgodnie z algorytmem x(k+1)=x(k)+αξ(k) najwyżej N kroków w kierunkach sprzężonych.

Metoda Newtona - Raphsona: (metoda iteracyjna, gradientowa)

Ustalenie wektora kierunku poszukiwań w punkcie, stanowiącym aktualne przybliżenie rozwiązania w ramach tej metody wymaga wyliczenia gradientu i (odwrotności) hesjanu badanej funkcji.
. Hesjan w danym punkcie jest macierzą kwadratową rozmiaru zgodnego z liczbą argumentów minimalizowanej funkcji, np. w przypadku funkcji dwu zmiennych ma postać:

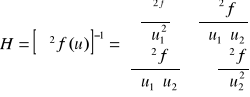
Metoda Newtona - Raphsona jest szczególnie skuteczną w bliskim otoczeniu punktu stanowiącego rozwiązanie zadania, natomiast zbliżamy się wolno, gdy jesteśmy w dalszej odległości od minimum.

Algorytm:

E1: Określ kierunek

E2: Znajdź minimum w danym kierunku

E3: Jeżeli znaleziono minimum t zmień kierunek d i wróć do E1.

Metoda Gaussa-Seidela

Jedną z najstarszych metod szukania punktu minimum funkcji bez warunków ograniczających jest metoda Gaussa-Seidla (G-S), nazywana także metodą re­laksacyjną. Jej zastosowanie jest ograniczone w zasadzie do wąskiej klasy funk­cji f (x), gdyż w metodzie tej zakłada się, że funkcja f (x) w otoczeniu punktu minimum musi być aproksymowana pewną ściśle wypukłą funkcją kwadratową.

Algorytm według tej metody przebiega następująco. Ustalając jedną ze składowych punktu x(0), np. przyjmując x₂=x₂(0), znaj­dujemy punkt minimum funkcji f(x₁,x₂(0)) jednej zmiennej x₁ czyli znajdujemy punkt x(1) = (x₁(1), x₂(1)) minimum wzdłuż, prostej o kierunku ξ(0) = (1,0), tj. wzdłuż osi Ox₁. Ustalamy teraz składową x₁= x₁(2) i znajdujemy punkt minimum funkcji f(x₁(1), x₂) jednej zmiennej x₂. Czyli z punktu x(1) poszukuje­my punktu minimum funkcji f(x₁,x₂) wzdłuż prostej o kierunku ξ(1) = (0,1), czyli wzdłuż osi Ox₂. Niech minimum to znajduje się w punkcie x(2) = (x₁(2), x₂(2)). Omówione postępowanie powtarzamy od początku traktując punkt x(2) jako nowy punkt x(0). Czynności te powtarzamy dopóty, dopóki nie osiągniemy szukanego punktu minimum.

22. Podaj (z uzasadnieniem) klasyfikację poznanych w trakcie wykładów algorytmów rozwiązywania zadania programowania nieliniowego. Jakie algorytmy zaliczamy do grupy metod kierunków sprzężonych?

Każdy problem optymalizacji statycznej spotykany w automatyce, który da się sformułować jako zadanie minimalizacji lub maksymalizacji funkcji wielu zmiennych z ograniczeniami równościowymi lub nierównościowymi, może być rozwiązany przy użyciu metod programowania nieliniowego lub liniowego.

Do grupy metod kierunków sprzężonych zaliczamy takie metody jak metoda: Fletchera Reavsa (gradientu sprzężonego), Powell'a, Davidona - Fletchera - Powella czy Persona.

Klasyfikując metody rozwiązywania zadań programowania nieliniowego możemy brać pod uwagę kilka cech, na przykład: metody gradientowe, oraz metody bezgradientowe, z innego punktu widzenia podziału możemy dokonać na metody kierunków sprzężonych i bez kierunków sprzężonych lub na zadania optymalizacji (rozwiązywane przecież za pomocą metod programowania nieliniowego) jednej zmiennej lub wielu zmiennych.

23. Na czym polega metoda simpleksów (Neldera-Meada) stosowana do rozwiązywania programo­wania nieliniowego? Przedstaw podstawową wersję sieci działań według tej metody.

Metoda simpleksów (rozwiązuje zadania programowania liniowego) jest programem badań typu bezgradientowego. Simpleksem nazywany jest regularny wielościan posiadający (n+1 wierzchołków - n jest tu liczbą argumentów funkcji kryterialnej, np. w przypadku dwu argumentów simpleksem jest trójkąt równoboczny, trzy optymalizowane czynniki prowadzą do czworościanu w przestrzeni trójwymiarowej, itd.

Na starcie poszukiwania ekstremum wykonuje się pomiary funkcji w wierzchołkach racjonalnie wybranego simpleksu początkowego. Następnie, w najprostszej wersji metody, na każdym kolejnym etapie minimalizacji wierzchołek z najmniej korzystnym położeniem - odpowiadający największej wartości funkcji - zostaje zamieniony nowym, położonym symetrycznie do niego, po przeciwstawnej ścianie simpleksu. W wyniku powtarzania tego działania, sympleks przesuwa się stopniowo w przestrzeni czynników wpływających na jakość optymalizowanego procesu. W sytuacji, gdy wynik pomiaru minimalizowanej funkcji w nowym wierzchołku jest gorszy od poprzedniego możemy zakończyć poszukiwanie lub kontynuować program po zmniejszeniu rozmiarów simpleksu. Efektywnym zakończeniem może być również wykonanie w znalezionym otoczeniu punktu stacjonarnego programu badań drugiego rzędu.

24. Przedstaw sformułowanie danego zadania programowania nieliniowego z zadanymi ogranicze­niami a także zmodyfikowaną postać optymalizowanej funkcji po uwzględnieniu „funkcji kary".

W metodach funkcji kary tworzymy zmodyfikowaną funkcję kryterialną przez dodanie do funkcji f(x) pewnej funkcji zwanej funkcją kary, stąd nazwa metody. Wartości funkcji kary reprezentują „karę” za niespełnienie warunków punktów dopuszczalnych. Zatem funkcja kary musi być dostosowana odpowiednio do postaci warunków ograniczających.

Ogólnie zmodyfikowaną funkcją kryterialną jest:

T(x,r)=f(x)+Φ(x,r), r∈(0, +∞)

Przy czym r - parametr, Φ(x,r) - funkcja kary.

Przypuśćmy, że zadanie polega na znalezieniu minimum funkcji f(x) jednej zmiennej przy warunkach ograniczających: a<=x<=b. W takiej sytuacji funkcja kary może może mieć jedną z 3 postaci:

25. W jaki sposób szerokość przedziału ufności przy pomiarze danej wielkości fizycznej w obecności addytywnych zakłóceń o rozkładzie normalnym zależy od wariancji zakłóceń i od liczby wykona­nych pomiarów?

Szerokość przedziału ufności przy pomiarze wielkości fizycznej szczególnie w obecności zakłóceń ma ogromne znacznie. Zwiększanie liczby pomiarów minimalizuje wariancję tych zakłóceń i to w dużym stopniu: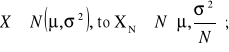
gdzie σ-wariancja błędu, N - liczba pomiarów.

26. Jaką charakterystyczną cechę posiadają elementy zbioru Pareto? Przedstaw interpretację graficzną optymalizacji wielo-wskaźnikowej.

Ha, i wiecie - jak wyszedłem z zerówki, to od razu zajarzyłem, o co w tym chodzi. Zbiór pareto jest zbiorem rozwiązań dopuszczalnych, a o najlepszym punkcie rozwiązania decyduje określony wskaźnik. Czyli, w zależności od rozpatrywanego przypadku (postawionego zadania) zależy rozwiązanie. W ogólnym przypadku, wydaje się, iż cały określony zbiór jest poprawnym rozwiązaniem optymalizacyjnym. Jednak, biorąc pod uwagę określone problemy zdefiniowane w zadaniu, okazuje się iż część przedziału będzie lepszejszym rozwiązaniem. A cały zbiór tych rozwiązań dopuszczalnych jest zwany zbiorem pareto.

Zbiór pareto to zbiór rozwiązań niezdominowanych.

27. Jakie czynniki uwzględnia się w ogólnym sformułowaniu problemu optymalizacji dynamicznej.

Ogólnie wyróżniamy dwa typy zadań:

1. Znalezienie optymalnego sterowania

2. Znalezienie optymalnego regulatora

Czynnikami uwzględnianymi w ogólnym sformułowaniu problemu optymalizacji dynamicznej są:

• Model
  
  

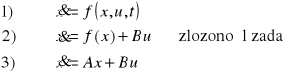
• Ograniczenia
  
  

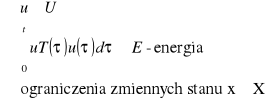
• Cel sterowania
  - sterowanie w określonym czasie i do określonego x_k
  - sterowanie do określonego punktu
  - sterowanie w określonym czasie
  - sterowanie, takie że w określonym czasie mamy znaleźć się w określonym punkcie funkcji.

• Wskaźnik jakości
  
  
  

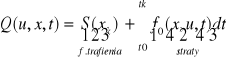
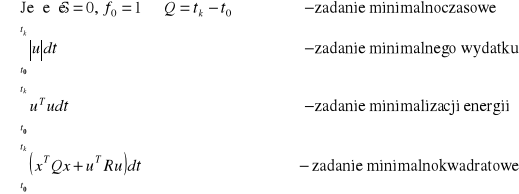
• Przedstaw zasadę optymalności i równanie Belmana wraz z jego interpretacją.

29. Przedstaw zasadę maksimum Pontriagina podając przy tym interpretację występujących tu pojęć.

Dany jest obiekt


Wskaźnik jakości: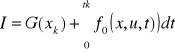


Wyznaczyć sterowanie u które minimalizuje I.

Wskaźnik jakości I osiągnie minimum (sterowanie będzie optymalnym) tylko wtedy, gdy istnieje niezerowa funkcja ψ* spełniająca wraz z x* i u* równanie:


które osiągnie maksimum w u*.


.
H - hamiltonian,

ψ - sprzężony wektor zmiennych stanu,

f₀ - funkcja strat chwilowych występująca we wskaźniku,

f - wektor prędkości zmian

30. Przedstaw sieć działań rozwiązywania zadania optymalizacji metodą programowania dynamicz­nego. Oceń skrócenie obliczeń przeprowadzanych tą metodą w stosunku do pełnego przeglądu możliwych wersji rozwiązania zadania.

31. Przedstaw ściśle sformułowanie zadania syntezy sterowania czasooptyrnalnego. Jakie rozwiązanie posiada to zadanie dla obiektów liniowego. Odpowiedź uzasadnij.

Ogólnie rzecz ujmując, zadania sterowania czasooptymalnego są formułowane:

Należy znaleźć sterowanie (wektor sterowań ) dla którego czas przejścia obiektu z zadanego stanu początkowego x(0)=x₀ do zadanego stanu końcowego x(t­_k)=x_k jest najkrótszy (minimalny)

Jeżeli dany jest wskaźnik jakości o postaci: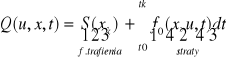

to zadanie czasooptymalne możemy zapisać jako:

Jeżeli S=0 f₀=1 → Q=t_k-t₀.; min


Rozwiązaniem zadania czasooptymalnego dla układów liniowych jest sterowanie przekaźnikowe. Ilość przełączeń (zmiana znaku składowych) dla liniowego, stacjonarnego obiektu, gdzie wszystkie jednokrotne wartości macierzy A są rzeczywiste wynosi co najwyżej n-1 razy.

32. Jakie sformułowanie i jakie rozwiązanie posiada zadanie syntezy sterowania na minimum wydat­ku dla obiektów liniowego. Odpowiedź uzasadnij.

Możemy sformułować: Jakie minimalne sterowanie możemy zastosować w celu przejścia obiektu ze stanu początkowego x₀=x(0) do stanu końcowego x_k. Na zadanie to mogą być nałożone dodatkowe ograniczenia w postaci przedziału czasu, poza który nie możemy wykroczyć.

min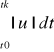
- zadanie minimalnego wydatku. Dla układów liniowych rozwiązaniem optymalnym tego problemu jest

33. Przedstaw sformułowanie zadania regulacji minimalnokwadratowej (LQR). Jakie rozwiązanie posiada zadanie syntezy regulatora tego typu? Jakie cechy posiadają macierze Q, R określające formy kwadratowe ze wskaźnika jakości regulacji? W jaki sposób możemy zinterpretować ele­menty diagonalne tych macierzy?


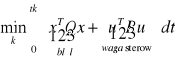
. Macierze Q i R są macierzami symetrycznymi, zawsze dodatnio określonym. Macierz Q (elementy na jej przekątnej) stabilizują daną zmienną stanu fizyczną, macierz jest macierzą odpowiadającą sile sterowania.

Rozwiązanie zadania syntezy kwadratowego sterowania optymalnego na tle teorii Lapunowa:

Spośród wielu różnych podejść do rozwiązania problemu optymalizacji opartej na wskaźnikach kwadratowych, zaprezentujemy podejście oparte na drugiej metodzie Lapunowa.

Druga metoda Lapunowa ma tę zaletę, że korzystanie z niej od podstaw przy rozwiązywaniu problemu syntezy optymalnych sprzężeń w systemie, gwarantuje jednocześnie automatycznie jego wynikową stabilność. Zapewniając w trakcie projektowania określone własności pochodnej funkcji Lapunowa danego autonomicznego systemu dynamicznego równocześnie sprawiamy, że jego wyjście będzie dążyło do zadanej wartości ustalonej.

Klasycznie natomiast rzecz ujmując, projekt regulatora wynika z określonej koncepcji syntezy układu sterowania zapewniającej przede wszystkim spełnienie warunków stabilności formułowanych z reguły w postaci dostatecznej (tzn. z zapasem), a dopiero w dalszej kolejności inne własności użytkowe projektowanego systemu. Istnieje także możliwość weryfikacji stabilności wynikowego systemu sterowania po przedstawieniu wersji projektu regulatora.

Rozważmy zadanie syntezy sterowania optymalnego obiektem opisanym równaniem:
na bazi kwadratowego wskaźnika jakości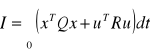
, co prowadzi jak wiemy do liniowej postaci sterowania u(t)=-Kx(t), gdzie K jest macierzą wzmocnień (r×n).

W związku z tym projekt optymalnego regulatora w systemie projektowym na bazie wskaźnika kwadratowego sprowadza się wyłącznie do określenia elementów macierzy K.

Optymalny system sterowania wynika z minimalizacji wskaźnika całkowego I, w którym macierz Q i R są kwadratowymi, symetrycznymi i dodatnio określonymi macierzami o elementach rzeczywistych. Zakładamy, że na sterowanie oraz zmienne stanu nie są nakłada ograniczenia.

Dobór elementów macierzy Q i R jest sprawą indywidualną każdego systemu. Ale przejdźmy do rzeczy (syntezy):




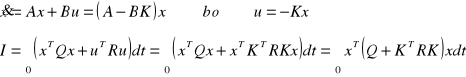
Lapunow, założył, że istnieje rzeczywista, symetryczna macierz P, określająca formę kwadratową, przy której dla każdego x zachodzi:







Jeżeli system jest liniowy i stabilny to z II metody Lapunowa, wiadomo, że zawsze istniej przynajmniej jedna dodatnio określona macierz P spełniająca określone równanie dla macierzy dodatnio określonych. Elementy macierzy P określamy z równania:




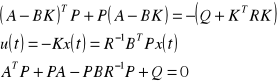
[K,P,E]=lqr(A,B,Q,R) → P - macierz będąca rozwiązaniem równania Riccatiego, E - macierz diagonalna wartości własnych macierzy [A-BK]. Jeżeli [A-BK] nie jest stabilną, to elementy K są nieokreślone (Not Number).

Algorytm:

E1: Rozwiąż równanie Riccatiego wyznaczając P. Sprawdź dodatnią określoność macierzy P - jeśli ok. to przejdź do E2, jeśli nie zmodyfikuj postać macierzy we wskaźniku

E2: Wstaw uzyskaną macierz P do równania
i wyznacz K, będzie ona zapewniać optimum sterowania (minimalizację I)

34. Przedstaw sformułowanie zadania optymalnej filtracji. Jakie rozwiązanie posiada to zadanie?

Filtracja optymalna opiera się na filtrze Kalmana.










35. Jaki związek istnieje między rozwiązaniem zadania znalezienia optymalnego regulatora typu LQR, a rozwiązaniem zadania optymalnej filtracji Kalmana?

36. Przedstaw równanie i schemat modelu procesu dynamicznego w postaci ARMAX.

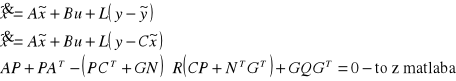
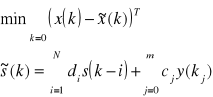
A(z^-1) y(i) = B(z^-1) u(i-d) + C (z^-1)  (i) ;




37. Wymień istotne zalety i wady regulacji minimalnowanancyjnej (MV). W jakich sytuacjach regu­lacja MV stanowi najbardziej racjonalne rozwiązanie problemu sterowania?

Regulacja minimalnowariancyjna jest formułowana dla obiektów modelowanych stochastycznie (np. model w strukturze ARMAX) w dwu wersjach:

• W wersji najprostszej celem jest generowanie ciągu sterowań u(k) minimalizującego wariancję wielkości regulowanej: min E{y²(k+d)

• W wersji bardziej skomplikowanej celem generowanego ciagu sterowań u(k) jest minimalizacja liniowej kombinacji (współczynnik ważący r) wariancji wielkości regulowanej i sterującej: min E {y²(k+d)+ru²(k)}

Regulacja tego typu stosowana jest w tych układach stabilizacji wielkości zadanej w których problemem podstawym jest obecność modelowanych np. przy pomocy wielomianu C(z^-1) w modelu CARMA zakłóceń stochastycznych. Sytuacja tego typu może zachodzić np. w układach wytłumiania silnych przypadkowych drgań (pojazdy, taśmociągi, itp.)

Rozwiązanie zadania regulacji MV związane jest możliwością kompensacji tych zaburzeń wielkości regulowanej, które wynikają z zakłóceń wygenerowanych przez otoczenia sterowanego procesu w przedziale czasowy sprzed taktu o numerze (k-d) - przypomnijmy, że k określa moment aktualny, d natomiast reprezentuje opóźnienie w równaniu obiektu.

Celem regulacji minimalnowariancyjnej jest minimalizacja wyrażenia E{y²(k+d). Optymalną wartość tego wyrażenia uzyskamy przy wyzerowaniu predykcji y_p(k+d|_k).

Wartość minimalizowanej wariancji wskazuje na graniczne możliwości wytłumiania zakłóceń w ramach regulacji minimalnowariancyjnej: E{y²(k+d)}=σ²(1+f₁²+…f²_d-1

Regulator minimalnowariancyjny wymaga dużego sterowania, co często mija się z celem. Jednak zastosowanie jego jest często bardzo skuteczne, bo nawet w granicach 90% poprawy.

38. Podaj definicję wskaźnika regulacyjności oceniającego jakość regulacji minimalnowanancyjnej. Od czego zależy osiągany poziom tego wskaźnika?

W celu minimalizacji wariancji wielkości regulowanej y(k) przy wymuszeniu w(k)=const, tj w celu rozwiązania zadania

Wielomiany na podstawie których wyznacza się parametry regulatora powinny spełniać równanie biofantyczne o postaci:
C=AF+Gz^-d, C,A,F,G - wielomiany
R=B⁺F, S=G, nF=d^-1

DODATEK:


- równanie Riccatiego


- rozwiązanie LQR dla wyznaczenia P

V(x)=x^TPx

V'(x)=x'^TPx+x^TPx'

A^TP+PA= - I - Równanie Lapunowa w postaci Ciągłej




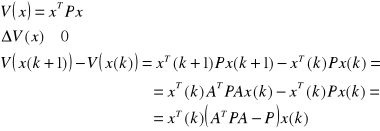
A^TPA-P = - Q - Równanie Lapunowa w postaci dyskretnej

24

Optymalizacja funkcji jednej zmiennej (bez zakłóceń)







---