Politechnika Wrocławska Wrocław, 18.01.2008

Wydział Geoinżynierii,

Górnictwa i Geologii

Schemat potencjalny sieci wentylacyjnej

Wykonali :

Marcin Jóżwik

Mateusz Stawaruk

Adam Lisowski

1. Wstęp

Dla wyznaczenia oporu rurociągu wychodzi się np. z potencjału izentropowego. Zgodnie z definicją jest on równy

(1)

gdzie:

- całkowity potencjał izentropowy, J/m³ ,

- ciśnienie całkowite w punkcie dla którego wyznaczamy potencjał, Pa,

- ciśnienie powietrza suchego (nieruchomego) ulegającego przemianie izentropowej w punkcie dla którego wyznaczamy potencjał, Pa, przy czym

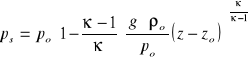
(2)

- ciśnienie statyczne, bezwzględne powietrza na zrębie szybu wdechowego, uważanym za główny wlot do sieci, Pa,

- wykładnik izentropy;
= 1,4,
g - przyspieszenie siły ciężkości; g = 9.80665 m/s² ,

ρ - gęstość powietrza na zrębie szybu wdechowego, kg/m³ ,

- wysokość niwelacyjna zrębu szybu wdechowego, m,
z - wysokość niwelacyjna punktu dla którego wyznaczamy potencjał, m.

Spadek całkowitego potencjału izentropowego
w bocznicy sieci wentylacyjnej wyznacza się z zależności:

(3)

gdzie:

- całkowity potencjał izentropowy w węźle dopływowym bocznicy (wyrobiska), J/m³ ,

- całkowity potencjał izentropowy w węźle wypływowym bocznicy (wyrobiska), J/m³.

Z teorii tego potencjału wiadomo [1], że jego spadek w ogólnym przypadku jest równy

(4)

gdzie:

- dyssypacja energii w bocznicy (wyrobisku), J/m³,

- dyssypacja energii w oporze lokalnym (miejscowym), J/m³,

- depresja naturalna generowana w bocznicy (wyrobisku), J/m³,

- spiętrzenie całkowitej energii wentylatora (praca techniczna doprowadzona do wentylatora), J/m³.

Dla prostoosiowego, poziomego odcinka (I - II) rurociągu bez wentylatora

= 0;
= 0 i
= 0

Wobec tego wzór (4) przyjmie postać

(5)

Dyssypację energii w bocznicy (wyrobisku) (pracę tarcia przypadającą na 1m³ przepływającego powietrza) wyznacza się z zależności

(6)

gdzie:

- gęstość powietrza wyznaczona dla warunków normalnych, t j. p = 760 Tr i t = 20°C,

= 1,20 kg/m³,

- gęstość średnia powietrza w bocznicy (wyrobisku) , kg/m³, równa

(7)

- odpowiednio gęstość powietrza w przekroju dopływu (d) i przekroju wypływu (w), kg/m3,

- strumień objętości powietrza sprowadzony do warunków normalnych, m³/s, przy czym

(8)

- strumień objętości powietrza, m³/s, wyznaczany ze wzoru

(9)

w - prędkość średnia powietrza w wyrobisku, m/s,

A - pole przekroju poprzecznego wyrobiska, m ,

- opór właściwy wyrobiska, kg/m⁷, przy czym

(10)

- liczba oporu wyrobiska,

B - obwód wyrobiska, m,

L - długość wyrobiska, m.

Chcąc wyznaczyć np. opór wyrobiska istniejącego, zgodnie z zależnościami (5÷10), należy, w oparciu o pomiary, wyznaczyć między innymi spadek całkowitego potencjału izentropowego powietrza.

Korzystając ze wzorów (3) i (1) można napisać

(11)

Dla wyrobiska (rurociągu) poziomego
, a tym samym zgodnie z

zależnością (2)
. W związku z tym wzór (11) przyjmie postać

(12)

Zgodnie z tą zależnością, spadek całkowitego potencjału izentropowego w tym przypadku jest równy różnicy ciśnień całkowitych pomierzonych w przekrojach dopływowym (d) i wypływowym (w) wyrobiska (rurociągu). Różnicę tą, można pomierzyć za pomocą, rurek Prandtla, grubościennego węża gumowego i przyrządu mierzącego różnicę ciśnień np. mikromanometru z rurką pochyłą .

Jeśli zamiast rurek Prandtla zastosujemy tarczki Sera to zgodnie z zależnością

(13)

dla wyznaczenia różnicy ciśnień całkowitych jest konieczny pomiar różnicy ciśnień statycznych (stosując tarczki Sera, grubościenny wąż gumowy i mikromanometr) oraz wyznaczenie różnicy ciśnień kinetycznych w oparciu o prędkości średnie i gęstości powietrza wyznaczone dla przekrojów dopływowego (d) i wypływowego (w) wyrobiska (rurociągDla sporzą

2.Opis stosowanych przyrządów:

1. mikromanometr z rurką pochyłą MPR-4

2. mikromanometr kompensacyjny MK-1 i mikromanometr MPR-4

3. rurka Prandtla (do pomiaru ciśnienia całkowitego w przekroju (d) )

4. rurka Prandtla (do pomiaru ciśnienia całkowitego i dynamicznego w przekroju (w) )

5. wentylator TD-500-160 (W-4)

6. wentylator TD-500-160 (W-3)

7. psychrometr Assmana

8. baroluks lub barometr rtęciowy

3. Stanowisko pomiarowe

Stanowisko do wyznaczania oporu rurociągu

4.Wyniki pomiarów:

Ciśnienie dynamiczne

Średnica rurociągu D = 160 mm = 0,16 m

Długość rurociągu l = 4,88 m

Temperatura sucha t_s = 25,2°C

Temperatura wilgotna t_w= 15,1°C

Ciśnienie

Różnica ciśnień całkowitych

Zmierzone ciśnienie w węzłach sieci

Węzeł	Ciśnienie
		l [mm]	Nachylenie	Pa
1	65	1/5	104,5389
3	88	1/5	141,5296
4	80	1/5	128,6632
6	77	1/5	123,8384
7	75	1/5	120,6218
8	104	1/5	167,2622
9	150	1/5	241,2436
11	160	1/5	257,3265
12	154	1/5	247,6768

5.Obliczenia

Obliczenie gęstości powietrza ρ:

tw = 15,2 st C

ts = 24,6 st C

p = 104 017,3563 [Pa]

• Obliczenia.

Wyznaczenie ciśnienia cząstkowego pary wodnej ze wzoru:

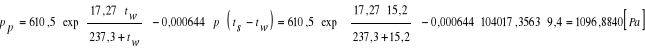
gdzie:

tw - temperatura na termometrze mokrym [C]

ts - temperatura na termometrze suchym [C]

p - ciśnienie statyczne powietrza [Pa]

Wyznaczenie stopnia zwilżenia ze wzoru:

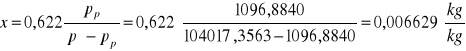
gdzie:

p_p - ciśnienie cząstkowe pary wodnej, [Pa],

p - ciśnienie statyczne bezwzględne powietrza, [Pa].

Wyznaczenie temperatury wirtualnej ze wzoru:

gdzie:

x - stopień zawilżenia [kg/kg]

T - temperatura powietrza [K]

T = t + 273,15=24,6+273,15=297,75 [K]

Wyznaczenie gęstości powietrza ze wzoru:

gdzie:

p - ciśnienie bezwzględne powietrza, [Pa], p = 104017,3563 [Pa]

R_a - stała gazowa, [J/(kg^.K)], R_a = 287, 04 [J/(kg^.K)]

T_v - temperatura wirtualna, [K]. T_v = 298,93[K]

Obliczenie prędkości (max)

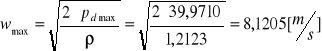
Obliczenie liczby Reynoldsa Re

gdzie:

D - średnia rurociągu D=0,16m

υ - lepkość kinematyczna powietrza υ = 15⋅10^-6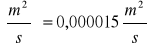

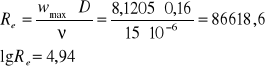
Ten stosunek wyznaczyłem z zależności:

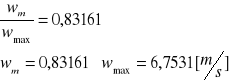
Obliczenie pola przekroju rurociągu

Obliczenie objętości powietrza

gdzie:

w_m -prędkość średnia powietrza w rurociągu

A - pole przekroju poprzecznego rurociągu

Obliczenie strumienia objętości powietrza w warunkach normalnych

gdzie:

- gęstość powietrza w warunkach normalnych

Wyznaczenie dyssypacji energii w rurociągu

gdzie:

l_fv - dyssypacja energii w rurociągu

l_flv - dyssypacja energii w oporze lokalnym (miejscowym) l_flv= 0

l_nv - dyssypacja naturalna generowana w rurociągu l_nv= 0

l_tv - spiętrzenie całkowite energii wentylatora l_tv= 0

Obliczenie oporu normalnego

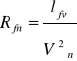
gdzie:

R_fn - opór normalny

- strumień objętości powietrza w warunkach normalnych

l_fv - dyssypacja energii w rurociągu

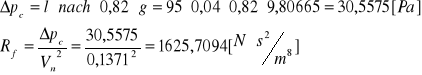
Obliczenie oporu właściwego rurociągu

Obliczenie liczby oporu wyrobiska λ_f oraz współczynnika oporu α_f

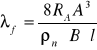
gdzie:

λ_f - liczba oporu rurociągu

α_f - współczynnik oporu

- gęstość powietrza dla warunku normalnego

R_f -opór właściwy rurociągu R_f =1642,3729

A - pole przekroju poprzecznego rurociągu A=0,0201 m²

B - obwód rurociągu B = πD = 3,14 ⋅ 0,16 = 0,5027 m

L - długość rurociągu L = 4,79m

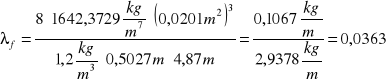
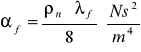
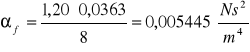
Obliczenie oporu tamy

t_w = 15,2°C

t_s = 24,6°C

p = 104017,3563 [Pa]

ρ = 1,2123 [kg/m³]

ρ_n = 1,2000 [kg/m³]

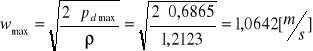
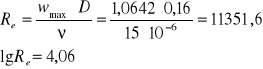
Ten stosunek wyznaczyłem z zależności:

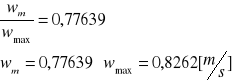
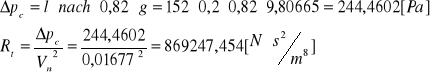
Wyniki pomiarów- ćwiczenie nr 5:

obliczenie gęstości powietrza w węzłach

Bocznica	wwęzłów	pp	x	Tv	ρ	pd
1	12,44223671	1097,584729	0,006638175	298,9359099	1,211349959	93,76409195
3	5,672767406	1097,972778	0,006644688	298,9370735	1,210598191	19,47870046
4	5,672767406	1097,89489	0,00664338	298,9368399	1,210749082	19,48112832
6	6,769469306	1097,70156	0,006640135	298,9362601	1,211123621	27,75030275
7	4,637741934	1097,691824	0,006639971	298,9362309	1,211142483	13,02502003
8	2,171698536	1098,061417	0,006646177	298,9373395	1,21042647	2,854351766
9	3,449872752	1098,489799	0,006653379	298,9386262	1,209596566	7,198080555
11	6,769469306	1098,68574	0,006656677	298,9392153	1,20921697	27,70661593
12	6,769469306	1098,617588	0,00665553	298,9390104	1,209349	27,70964112

t_w = 15,2°C

t_s = 24,6°C

p = 104017,3563 [Pa]

ρ = 1,2123 [kg/m³]

ρ_n = 1,2000 [kg/m³]

Wyznaczenie ciśnienia cząstkowego pary wodnej ze wzoru:

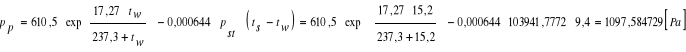
Wyznaczenie stopnia zwilżenia ze wzoru:

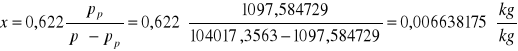
Wyznaczenie temperatury wirtualnej ze wzoru:

gdzie:

x - stopień zawilżenia [kg/kg]

T - temperatura powietrza [K]

T = t + 273,15=24,6+273,15=297,75 [K]

=

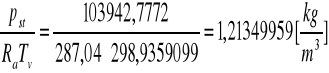
Zmierzone prędkości w bocznicach sieci

Bocznica	Prędkość
		[m/s]
A 3	6,6 - 6,8
0 1	11,5 - 11,7
1 6	6,8 - 7,0
6 B	2,3 - 2,5
7 8	2,5 - 2,7
C 9	3,5 - 3,7
9 11	7,4 - 7,6

obliczenie strumienia objętości V oraz strumienia objętości powietrza dla warunków normalnych V_n w bocznicach wg poniższych wzorów:

Bocznica	w max		w max	D	Re	lg Re	wśr/wmax	w śr	A	V	Vn
		m/s		m/s				[m]				[m/s]	[m^2]	[m^3/s]	[m^3/s]
A 3	6,6	6,8	6,7	0,16	71 466,67	4,85	0,82904	5,55454	0,0201	0,11165	0,11647
0 1	11,5	11,7	11,6	0,16	123 733,33	5,09	0,8355	9,69175	0,0201	0,19480	0,23316
1 6	6,8	7,0	6,9	0,16	73 600,00	4,87	0,82945	5,72322	0,0201	0,11504	0,13869
6 B	2,3	2,5	2,4	0,16	25 600,00	4,41	0,80734	1,93763	0,0201	0,03895	0,04824
7 8	2,5	2,7	2,6	0,125	21 666,67	4,34	0,80218	2,08568	0,0122	0,02545	0,01431
C 9	3,5	3,7	3,6	0,16	38 400,00	4,58	0,81778	2,944	0,0201	0,05917	0,07236
D 11	7,4	7,6	7,5	0,16	80 000,00	4,90	0,83059	6,22941	0,0201	0,12521	0,15157

Przykładowe obliczenie dla bocznicy A 3

Obliczenie liczby Reylnoldsa ze wzoru:

w_max - prędkość maksymalna powietrza w rurociągu [m/s] w_max = 6,7 [m/s]

D - średnica rurociągu [m] D = 0,16 [m]

V - lepkość kinematyczna v = 15^.10^-6 [m²/s]

Ten stosunek wyznaczyłem z zależności:

Obliczenie średniej prędkości powietrza w rurociągu:

Obliczenie strumienia objętości powietrza:

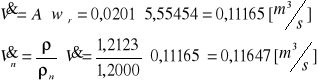
Wyznaczenie potencjałów w węzłach sieci.

Węzeł	wysokość	pb	pst	pc	ps	hcs
0	126,8	104017,3563	104 017,3563	104 017,3563	104017,3563	0,0000
1	124,45	104046,3161	103 941,7772	104 035,5413	104045,3241	-9,7828
3	126,65	104019,2046	103 877,6750	103 897,1537	104019,1413	-121,9876
4	126,65	104019,2046	103 890,5413	103 910,0224	104019,1413	-148,1444
6	124,45	104046,3161	103 922,4777	103 950,2280	104045,3241	-95,0961
7	124,45	104046,3161	103 924,0860	103 937,1110	104045,3241	-108,2130
8	125,75	104030,2948	103 863,0326	103 865,8869	104029,8519	-163,9650
9	125,75	104030,2948	103 792,2678	103 799,4659	104029,8519	-230,3860
11	126,68	104018,8349	103 759,9001	103 787,6067	104018,7843	-231,1776
12	126,68	104018,8349	103 771,1582	103 798,8678	104018,7843	-275,3864

Gdzie:

p_b - ciśnienie barometryczne [Pa]

p_st - ciśnienie statyczne [Pa]

p_s - ciśnienie statyczne powietrza suchego [Pa]

Przykładowe obliczenie dla węzła 0:

• Obliczenie ciśnienia barometrycznego ze wzoru:

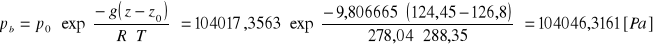
p₀ - ciśnienie atmosferyczne na zrębie szybu wdechowego [Pa]

z - wysokość niwelacyjna punktu dla którego wyznaczamy ciśnienie [m]

z₀ - wysokość niwelacyjna na zrębie szybu wdechowego [m]

R - stała gazowa

T - temperatura [K]

p₀ = 104017,3563 [Pa]

z = 126,8 [m]

z₀ =126,8 [m]

R - 278,04

T - 297,75 [K]

• Obliczenie rzeczywistego ciśnienia statycznego:

p_b - ciśnienie barometryczne [Pa]

p_przy - ciśnienie wskazane przez przyrząd pomiarowy [Pa]

p_b =104046,3161[Pa]

p_przy =104,5389 [Pa]

• Obliczenie ciśnienia powietrza suchego:

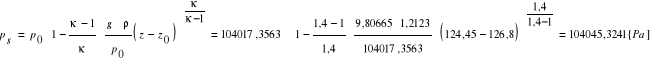
p₀ - ciśnienie atmosferyczne na zrębie szybu wdechowego [Pa]

z - wysokość niwelacyjna punktu dla którego wyznaczamy ciśnienie [m]

z₀ - wysokość niwelacyjna na zrębie szybu wdechowego [m]

κ - wykładnik izentropy

p₀ = 104017,3563 [Pa]

z = 124,45 [m]

z₀ =126,8 [m]

κ - 1,4

ρ = 1,2123 [kg/m³]

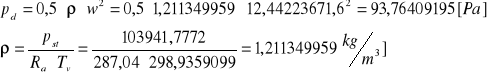
Bocznica	wwęzłów	pp	x	Tv	ρ	pd
1	12,44223671	1097,584729	0,006638175	298,9359099	1,211349959	93,76409195
3	5,672767406	1097,972778	0,006644688	298,9370735	1,210598191	19,47870046
4	5,672767406	1097,89489	0,00664338	298,9368399	1,210749082	19,48112832
6	6,769469306	1097,70156	0,006640135	298,9362601	1,211123621	27,75030275
7	4,637741934	1097,691824	0,006639971	298,9362309	1,211142483	13,02502003
8	2,171698536	1098,061417	0,006646177	298,9373395	1,21042647	2,854351766
9	3,449872752	1098,489799	0,006653379	298,9386262	1,209596566	7,198080555
11	6,769469306	1098,68574	0,006656677	298,9392153	1,20921697	27,70661593
12	6,769469306	1098,617588	0,00665553	298,9390104	1,209349	27,70964112

• Obliczenie potencjału statycznego w węźle 1:

Potencjały w bocznicach sieci:

Bocznica	δhs
0 1	9,7828
1 6	85,3133
6 8	68,8689
11 12	44,2088
1 3	112,2049
6 7	13,1170
7 8	55,7519
8 9	66,4211
7 9	122,1730
9 11	0,7916
3 4	26,1567

gdzie:

h _d - potencjał izentropowy w węźle dopływu

h _w - potencjał izentropowy w węźle wypływu

Depresje naturalne w bocznicach sieci

Bocznica	zd	zw	psd	psw	ln
0 1	126,8	124,45	104017,3563	104045,3241	-0,0306
1 6	124,45	124,45	104045,3241	104045,3241	0
6 8	124,45	125,75	104045,3241	104029,8519	0,017604
11 12	126,68	126,68	104018,7843	104018,7843	0
1 3	124,45	126,65	104045,3241	104019,1413	0,028828
6 7	124,45	124,45	104045,3241	104045,3241	0
7 8	124,45	125,75	104045,3241	104029,8519	0,017604
8 9	125,75	125,75	104029,8519	104029,8519	0
7 9	124,45	125,75	104045,3241	104029,8519	0,017604
9 11	125,75	126,68	104029,8519	104018,7843	0,011585
3 4	124,45	124,45	104019,1413	104019,1413	0

gdzie:

z_d - wysokość niwelacyjna węzła dopływu [m]

z_w - wysokość niwelacyjna węzła wypływu [m]

p_sw - ciśnienie statyczne powietrza suchego węzła wypływu [Pa]

p_sd - ciśnienie statyczne powietrza suchego węzła dopływu [Pa]

Dyssypacje energii w bocznicach sieci

Bocznica	δh	ln	lt	lf
0 1	9,7828	-0,0306		9,7522
1 6	85,3133	0,0000		85,3133
6 8	68,8689	0,0176		68,8865
11 12	44,2088	0,0000	247,677	291,8856
1 3	112,2049	0,0288	128,663	240,8969
6 7	13,1170	0,0000		13,1170
7 8	55,7519	0,0176		55,7695
8 9	66,4211	0,0000		66,4211
7 9	122,1730	0,0176		122,1906
9 11	0,7916	0,0116		0,8031
3 4	26,1567	0,0000		26,1567

gdzie:

l_n - depresja naturalna

l_t - praca techniczna wentylatora

δh - spadek potencjału

obliczenie oporu normalnego i właściwego

Bocznica	lf	Rf	Rn	Vnwyr	wwęzłach
0 1	9,7522	153	151	0,252643	12,44224
1 6	85,3133	4 515	4 470	0,137456	6,769469
6 8	68,8865	36 767	36 395	0,043285	2,131727
11 12	291,8856	15 448	15 292	0,137456	6,769469
1 3	240,8969	18 156	17 973	0,115187	5,672767
6 7	13,1170	1 479	1 464	0,094171	4,637742
7 8	55,7695	77 849	77 062	0,026765	2,171699
8 9	66,4211	13 536	13 399	0,070051	3,449873
7 9	122,1906	26 894	26 622	0,067405	3,319597
9 11	0,8031	43	42	0,137456	6,769469
3 4	26,1567	1 971	1 951	0,115187	5,672767

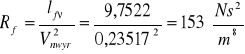
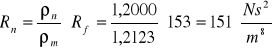
ρ_m - gęstość powietrza w bocznicy [kg/m³], ρ_m = 1,2123[kg/m³]

ρ_n - gęstość powietrza dla warunków normalnych [kg/m³], ρ_n = 1,2000 [kg/m³]

V_n - strumień objętości powietrza [m³/s],

R_f - opór właściwy [Ns²/m⁸]

R_n - opór normalny [Ns²/m⁸]

Wyrównanie V_n

Wyrównałem za pomocą narzędzia „SOLVER” w excelu

					Maksymalna
	Vnmin	Vnmin	Vnmax	Vnmax	odchyłka		Vnśr	Vnśr/min
0-1	0,23115	13,869	0,23517	14,1102	0,1206	0-1	0,23316	13,9896
1-3	0,13266	7,9596	0,13668	8,2008	0,1206	1-3	0,13467	8,0802
1-6	0,13668	8,2008	0,1407	8,442	0,1206	1-6	0,13869	8,3214
6-8	0,04623	2,7738	0,05025	3,015	0,1206	6-8	0,04824	2,8944
7-8	0,0305	1,83	0,03294	1,9764	0,0732	7-8	0,03172	1,9032
7-9	0,07035	4,221	0,07437	4,4622	0,1206	7-9	0,07236	4,3416
9-11	0,14874	8,9244	0,15276	9,1656	0,1206	9-11	0,15075	9,045
						6-7
						8-9

Zmieniać	Wyniki		Vnwyr
dVn	Vnwyr	dVn	[m^3/s]
1,168976	15,158576	1,168976134	0,252643
-1,168977	6,9112233	-1,168976672	0,115187
-0,074047	8,2473528	-0,074047194	0,137456
-0,297282	2,5971176	-0,297282423	0,043285
-0,297282	1,6059176	-0,297282386	0,026765
-0,297282	4,0443176	-0,297282386	0,067405
-0,797647	8,2473528	-0,797647194	0,137456
	5,6502352		0,094171
	4,2030352	Suma kwadratrów	0,070051
Węzeł	Bilans	3,639866167
1	0,00000
6	0,00000
7	0,00000
8	0,00000
9	0,00000

Dyskusja błędów

Błędy, które mogły powstać przy opracowywaniu wyników mogły być spowodowane niedokładnościami pomiarowymi. Błędy pomiarowe mogą wynikać zarówno z niedokładności sprzętu pomiarowego jak również z niedokładności dokonujących pomiary.

Wnioski:

Po przeprowadzeniu obliczeń można stwierdzić, że pomiary zostały przeprowadzone prawidłowo, gdyż potencjały we wszystkich węzłach mają wartość ujemną, natomiast spadki potencjałów w bocznicach są dodatnie. Depresje naturalne w bocznicach 1-6, 6-7 i 8-9 mają wartość 0, ponieważ bocznice te są poziome. Do obliczania oporów bocznic przyjęto wyrównane strumienie objętości powietrza po to by strumienie w sieci bilansowały się.

2

1

2

5

13

10

12

9

7

6

3

4

0

11

9

150

100

h_cs [Pa]

13

10

12

0

1

3

4

6

7

8

5

50

100

150

200

250

h_cs[Pa]

---