Ćwiczenie nr 30
Wyznaczanie współczynnika rozszerzalności liniowej ciał stałych
Opracowanie wyników
Obliczenia dla próbki pierwszej
Obliczam wartość średnią długości początkowej l0 oraz niepewność pomiarową Δl0 metodą statystyczną.
Pomiaru dokonywałem linijką o podziałce 1 mm.
Błąd wyniku średniego wyznaczam stosując wzór na błąd średni kwadratowy
Jest to błąd wyznaczania długości początkowej , ale ponieważ przyrząd mierniczy ma większy błąd, zatem przyjmuję
Obliczam dla wszystkich temperatur t przyrosty temperatur δt = t - t0 i przyrosty długości
δl = l - l0. Określam niepewności pomiarowe Δ(δt) i Δ(δl).
Niepewność pomiaru temperatury wynika z błędu odczytu danej wartości z termometru, który to błąd jest wielkością podziałki czyli w tym przypadku Δ(δt) = 0,5 °C.
Niepewność pomiaru wydłużenia pręta wynika z błędu odczytu wartości wskazanej przez czujnik zegarowy, którego dokładność przyjmuję za ową niepewność Δ(δl) = 0,01 mm.
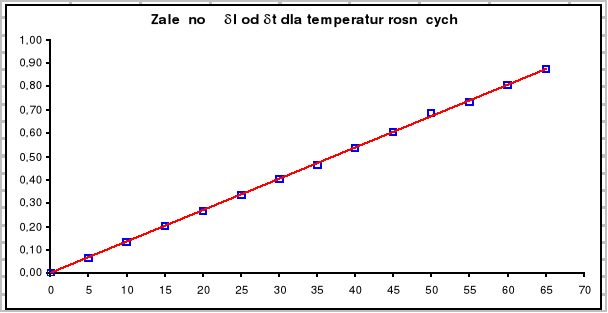
Wyznaczam współczynnik nachylenia wykresu (δl : δt), dla temperatur rosnących, metodą regresji liniowej. Nachylenie a ma postać
Wyznaczam odchylenie standardowe (δl : δt) z wzoru
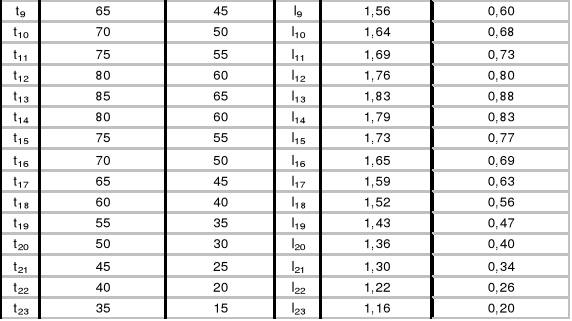
Wyznaczam współczynnik nachylenia wykresu (δl : δt), dla temperatur malejących, metodą regresji liniowej. Nachylenie a ma postać
Wyznaczam odchylenie standardowe (δl : δt) z wzoru
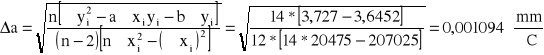
Obliczam wartość współczynnika rozszerzalności liniowej α i błąd wyniku Δα metodą różniczki zupełnej.
Dla temperatur rosnących
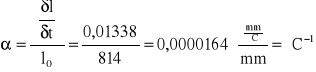
Dla temperatur malejących
Obliczenia dla próbki drugiej
Obliczam wartość średnią długości początkowej l0 oraz niepewność pomiarową Δl0 metodą statystyczną.
Pomiaru dokonywałem linijką o podziałce 1 mm.
Błąd wyniku średniego wyznaczam stosując wzór na błąd średni kwadratowy
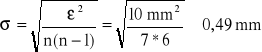
Jest to błąd wyznaczania długości początkowej , ale ponieważ przyrząd mierniczy ma większy błąd, zatem przyjmuję
Obliczam dla wszystkich temperatur t przyrosty temperatur δt = t - t0 i przyrosty długości
δl = l - l0. Określam niepewności pomiarowe Δ(δt) i Δ(δl).
Niepewność pomiaru temperatury wynika z błędu odczytu danej wartości z termometru, który to błąd jest wielkością podziałki czyli w tym przypadku Δ(δt) = 0,5 °C.
Niepewność pomiaru wydłużenia pręta wynika z błędu odczytu wartości wskazanej przez czujnik zegarowy, którego dokładność przyjmuję za ową niepewność Δ(δl) = 0,01 mm.
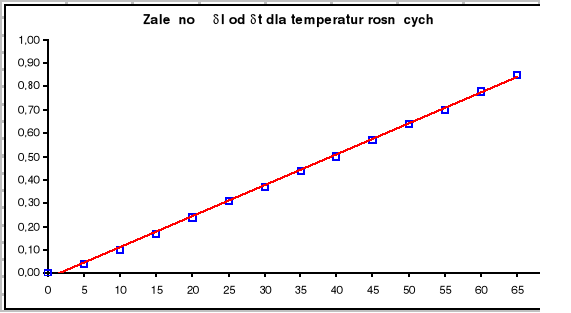
Wyznaczam współczynnik nachylenia wykresu (δl : δt), dla temperatur rosnących, metodą regresji liniowej. Nachylenie a ma postać
Wyznaczam odchylenie standardowe (δl : δt) z wzoru
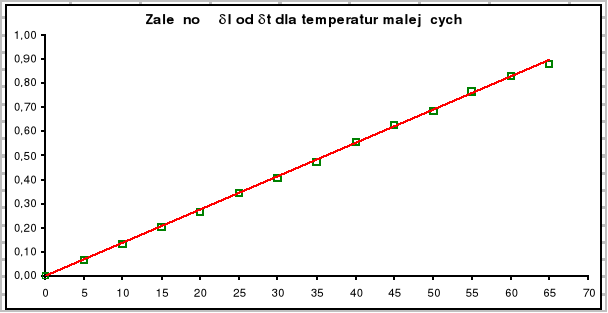
Wyznaczam współczynnik nachylenia wykresu (δl : δt), dla temperatur malejących, metodą regresji liniowej. Nachylenie a ma postać
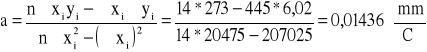
Wyznaczam odchylenie standardowe (δl : δt) z wzoru
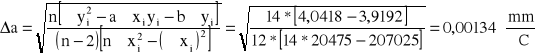
Obliczam wartość współczynnika rozszerzalności liniowej α i błąd wyniku Δα metodą różniczki zupełnej.
Dla temperatur rosnących
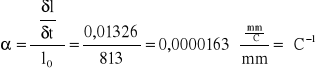
Dla temperatur malejących
Obliczenia dla próbki trzeciej
Obliczam wartość średnią długości początkowej l0 oraz niepewność pomiarową Δl0 metodą statystyczną.
Pomiaru dokonywałem linijką o podziałce 1 mm.
Błąd wyniku średniego wyznaczam stosując wzór na błąd średni kwadratowy
Jest to błąd wyznaczania długości początkowej , ale ponieważ przyrząd mierniczy ma większy błąd, zatem przyjmuję
Obliczam dla wszystkich temperatur t przyrosty temperatur δt = t - t0 i przyrosty długości
δl = l - l0. Określam niepewności pomiarowe Δ(δt) i Δ(δl).
Niepewność pomiaru temperatury wynika z błędu odczytu danej wartości z termometru, który to błąd jest wielkością podziałki czyli w tym przypadku Δ(δt) = 0,5 °C.
Niepewność pomiaru wydłużenia pręta wynika z błędu odczytu wartości wskazanej przez czujnik zegarowy, którego dokładność przyjmuję za ową niepewność Δ(δl) = 0,01 mm.
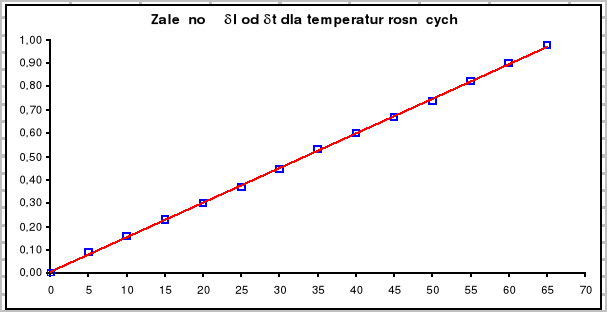
Wyznaczam współczynnik nachylenia wykresu (δl : δt), dla temperatur rosnących, metodą regresji liniowej. Nachylenie a ma postać
Wyznaczam odchylenie standardowe (δl : δt) z wzoru
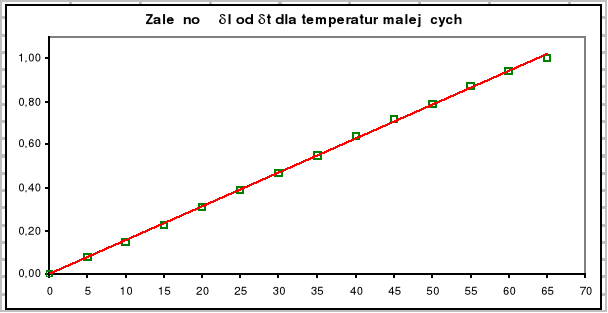
Wyznaczam współczynnik nachylenia wykresu (δl : δt), dla temperatur malejących, metodą regresji liniowej. Nachylenie a ma postać
Wyznaczam odchylenie standardowe (δl : δt) z wzoru
Obliczam wartość współczynnika rozszerzalności liniowej α i błąd wyniku Δα metodą różniczki zupełnej.
Dla temperatur rosnących
Dla temperatur malejących
Porównując otrzymane wyniki z danymi tablicowymi wnioskuję, że:
próbka pierwsza (α=0,0000164; α=0,0000162; Δα=0,00000143; Δα=0,00000136) biorąc pod uwagę wygląd (kolor) tego materiału to stal nierdzewna (α=0,000016)
próbka druga (α=0,0000163; α=0,0000177; Δα=0,00000126; Δα=0,00000167) biorąc pod uwagę wygląd (kolor) tego materiału to miedź (α=0,000016)
próbka trzecia (α=0,0000193; α=0,0000203; Δα=0,00000134; Δα=0,00000126) biorąc pod uwagę wygląd (kolor) tego materiału to mosiądz (α=0,000018)
1
10
Wyszukiwarka