ELEMENTY OPTOELEKTRONIKI

SOCZEWKI ŚWIATŁOWODOWE

Wykonał:

Dariusz Ostapiuk

E.D.8.3

LUBLIN 1998 r.

Osiągnięcia techniki światłowodowej doprowadziły do powstania nowoczesnych czujników wielkości fizycznych, charakteryzujących się zastosowaniem światłowodów w ich konstrukcji. W systemach czujników ważne miejsce zajmuje soczewka światłowodowa, która w elemencie czujnika może wypełniać rolę kolimatora lub elementu ogniskującego wiązkę światła. Niniejszy referat poświęcony jest omówieniu własności soczewek światłowodowych decydujących o ich szerokim zastosowaniu.

W optyce konwencjonalnej, aby uzyskać skupienie w ognisku rozbieżnej wiązki promieni świetlnych konieczne jest odpowiednie ukształtowanie powierzchni materiału optycznego, tak jak dzieje się to w soczewkach objętościowych. Współczynnik załamania materiału soczewki pozostaje stały, lecz wymagane jest aby był inny niż współczynnik załamania środowiska. W soczewkach światłowodowych modelowanie kształtu zastępuje się modelowaniem współczynnika załamania światła. W efekcie powstaje element optyczny współmierny geometrycznie ze światłowodem, spełniający rolę soczewki. Soczewka światłowodowa to soczewka w kształcie cylindra o średnicy 0,5-3 [mm] i długości 3-30 [mm] w zależności od przeznaczenia. Formowanie frontu falowego odbywa się dzięki gradientowemu profilowi refrakcyjnemu, przy czym maksymalna wartość współczynnika załamania światła występuje w osi soczewki (tak jak w światłowodach gradientowych). Stąd pochodzi jej nazwa GRIN (od gradient index ang.).

Sposób tworzenia się ogniska w soczewce konwencjonalnej

Sposób tworzenia się ogniska w soczewce gradientowej

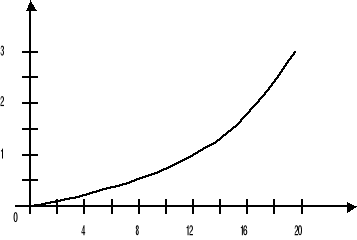
Podstawową metodą analizy soczewek światłowodowych jest przybliżenie optyki geometrycznej. Profil rozkładu współczynnika załamania światła w soczewce opisuje się zależnością:

n²(r)=n²(0)[1-(gr)²+h₄(gr)⁴+h₆(gr)⁶+.....]

gdzie: h₄, h₆ - współczynniki rozwinięcia

Trajektorie promieni soczewki GRIN obliczamy, rozwiązując równanie promienia:

przy założonych warunkach brzegowych
.

Z analizy równania promieni wynika, że wszystkie promienie południkowe będą ogniskowane, jeżeli n(r) będzie w postaci

n²(r)=n²(0)sech² (δr/R)

przy czym δ jest parametrem uwzględniającym gradientowy rozkład współczynnika załamania światła. Rozwijając sech² (δr/R) w szereg, otrzymamy wyrażenie profilu ogniskującego promienie przyosiowe południkowe

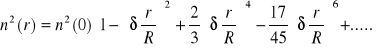
Dla promieni skrośnych optymalny profil n(r) określa się zależnością

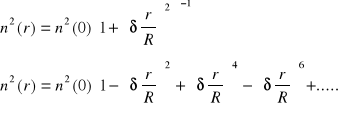
po rozwinięciu w szereg otrzymujemy dla strefy przyosiowej.

Z porównania tych wzorów wynika, że optymalny profil n(r) opisany równaniem pierwszym będzie dla promieni przyosiowych południkowych, gdy h₄=2/3, h₆=-17/45, a dla promieni skrośnych biegnących w pobliżu brzegu soczewki, gdy h₄=1, h₆=-1.Promienie skrośne w pobliżu osi odgrywają znikomą rolę to też można je zaniedbać. Wówczas oznaczając A=g² otrzymujemy wyrażenie na profil soczewki w pierwszym przybliżeniu

gdzie: n(0)- współczynnik załamania światła w osi optycznej

A()- dodatnia stała zwana stałą rozkładu n(r)

r- promień soczewki

Współczynnik załamania światła wewnątrz soczewki zmienia się w ten sposób, aby promień świetlny propagował w niej po drodze o kształcie sinusoidalnym. Stała A() chociaż nie ma fizycznej interpretacji charakteryzuje sposób zmian współczynnika załamania światła i w efekcie określa właściwości soczewki. Jest ona podawana częściej przez producenta w postaci
, przy danej długości fali.

Trajektorie promieni w strukturze GRIN oblicza się rozwiązując równanie promieni, które po uwzględnieniu profilu refrakcyjnego sprowadza się do równania

Uwzględniając warunki brzegowe
oraz równanie Snella uzyskuje się opis trajektorii promieni w postaci macierzowej.

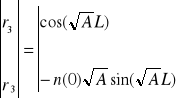
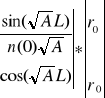
rys. Opis ten stanowi podstawę do określenia parametrów i charakterystyk soczewek światłowodowych.

Jeśli na soczewkę pada wiązka promieni biegnących równolegle do jej osi, to powyższe równanie upraszcza się

Jak zostało wspomniane promienie świetlne biegnące przez strukturę GRIN posiadają trajektorię sinusoidalną o okresie P

Parametr ten służy do określania długości soczewki światłowodowej w zależności od wymagań aplikacyjnych. Poniżej przedstawiono kilka typowych wariantów soczewek spełniających funkcję ogniskowania i kolimacji optycznych.

0,23P 0,25P 0,29P

0,5P 0,5P

Długość soczewki jest wprost proporcjonalna do długości trajektorii jaką zakreśla promień świetlny.

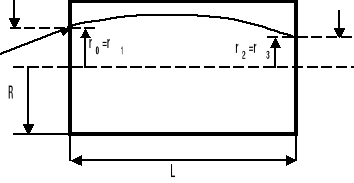
Równania w postaci macierzowej umożliwiają określenie pozycji i kąta wyjścia promienia z soczewki, jeśli znamy pozycję i kąt wejścia promienia. Równania te pozwalają opisać soczewkę światłowodową podobnie jak soczewkę grubą w optyce klasycznej. Na poniższym rysunku przedstawiono wielkości charakteryzujące parametry geometryczne soczewki światłowodowej. Położenie ogniska F₁, F₂ obrazu L₁, L₂ i płaszczyzn głównych P₁, P₂ zależy od wartości współczynnika załamania na osi soczewki, długości soczewki i parametru profilu A.

rys. Parametry soczewek.

Podstawowe charakterystyki tych zależności to:

-Ogniskowa (odległość od płaszczyzny głównej P₁ lub P₂ do ogniska F₁ lub F₂)

-Odległość pracy S_1,2 (inaczej ”Czołowa”- odległość od czoła soczewki do ogniska )

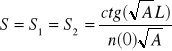
Należy zwrócić uwagę że w zakresie 0,5 <
L< oraz 1,5<
L< wartość S jest ujemna, co oznacza, że ognisko jest wewnątrz soczewki.

-Położenie płaszczyzny głównej h=h₁=h₂

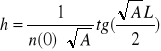
-Apertura numeryczna. Kąt padania promienia akceptowanego przez soczewkę światłowodową osiąga (analogicznie, jak w światłowodzie gradientowym) maksymalną wartość, gdy promień pada w centrum soczewki i maleje w miarę padania coraz bliżej brzegu. Aperturę numeryczną NA definiuje się analogicznie jak w światłowodzie

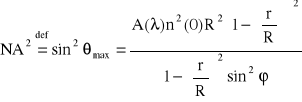
gdzie ϕ- kąt padania promieni skrośnych.

Pomijając promienie skrośne (ϕ=0),otrzymamy

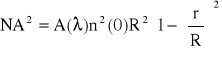
skąd maksymalna wartość apertury numerycznej dla r=0 wynosi

NA=
n(0)R

W przypadku uwzględnienia pełnej wiązki światła posługujemy się aperturą numeryczną efektywną

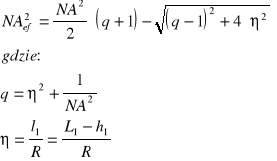
W soczewce będą prowadzone jedynie promienie padające na jej czoło pod kątem mniejszym od θ_ef.

-Powiększenie (m=L₂/L₁)

Jeżeli m<0, to powstający obraz jest odwrócony. Przy określonych parametrach soczewki powiększenie maleję wraz ze wzrostem odległości przedmiotu od czoła soczewki.

FUNKCJE TECHNICZNE SOCZEWEK

Można wyróżnić trzy podstawowe funkcje techniczne jakie mogą spełniać soczewki światłowodowe w zastosowaniach optoelektronicznych. Są to:

a) Transformacja apertury numerycznej

b) Ogniskowanie i kolimacja

c) Transformacja położenia i kąta padania.

Transformacja apertury numerycznej polega na kształtowaniu kąta rozbieżności źródła światła. Efekt transformacji apertury bywa stosowany do zwiększania skuteczności sprzężenia optycznego źródło-światłowód

Wiązka światła ze źródła o aperturze numerycznej wejściowej NA_we zostaje przetransponowana w wiązkę o wyjściowej aperturze numerycznej NA_wy. Zmiana apertury numerycznej jest zależna od stopnia powiększenia obrazu według zależności

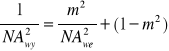
Efekt transformacji NA wykorzystuje się do sprzęgania laserów półprzewodnikowych ze światłowodami jednomodowymi. Ze względu na duża rozbieżność wiązki wychodzącej ze źródła dąży się do wykonania soczewek o dużej aperturze numerycznej lub w wersji PC (plano-convex). Dla źródeł, których średnica powierzchni czynnej jest mniejsza od średnicy sprzęganego światłowodu, obniża się aperturę numeryczną wyjściową dopasowując ją do apertury numerycznej światłowodu. W efekcie uzyskuje się polepszenie sprawności względem sprzężenia „na styk” oraz obniżenie wymagań technicznych dotyczących precyzji ustawiania sprzęganych elementów względem siebie. Na tej samej zasadzie działają sprzęgacze światłowód-światłowód.

Drugą istotną funkcją soczewki światłowodowej jest ogniskowanie i kolimacja wiązek promieni. Dąży się do uzyskania możliwie małych wymiarów średnicy planki świecenia w ognisku. Charakter propagacji światła wprowadza ograniczenie dyfrakcyjne na szerokość połówkową średnicy planki.

D_dyf=1,22/NA

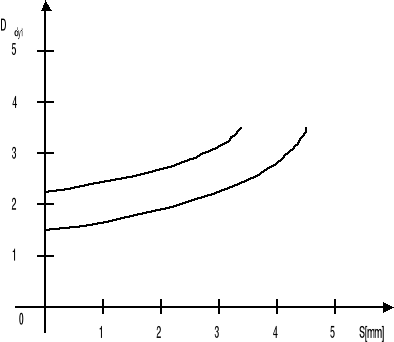
rys. Zależność ograniczenia dyfrakcyjnego średnicy plamki w funkcji odległości pracy.

Przyjmując długość soczewki L=0,25P otrzymamy

D_dyf=1,22f/R

gdzie f- ogniskowa, D_dyf- szerokość połówkowa w ognisku. W aplikacjach często stosuje się L<0,25P (np. 0,23P ). Ognisko wystąpi wówczas w odległości S od czoła soczewki a szerokość połówkowa plamki świecenia wynikająca z ograniczenia dyfrakcyjnego będzie wynosić

Dla rzeczywistych soczewek profil n(r) różni się od rozkładu idealnego, stąd ograniczenie na średnicę plamki w ognisku

D_ab=0,084(h₄-2/3)L(gR)³

Przy kolimacji wiązki światła decydującą rolę odgrywają parametry fizyczne soczewki gradientowej oraz rozmiary źródła. Kąt odchylenia promienia Δθ od tworzącej walce soczewki wynosi

Δθ=n(0)
r_f

gdzie r_f- promień średnicy padającej wiązki (np. promień światłowodu).

W rzeczywistości o wielkości plamki rozmycia ogniska decyduje jakość struktury GRIN, a w szczególności profil rozkładu współczynnika załamania światła. Wysokiej klasy soczewki światłowodowe mają rozmycie ogniska rzędu kilku mikrometrów.

Efekt kolimacji w soczewkach światłowodowych wykorzystuje się do połączeń optycznych z przerwą, w którą można wstawiać element fizyczny oddziałujący z światłem.

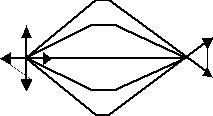
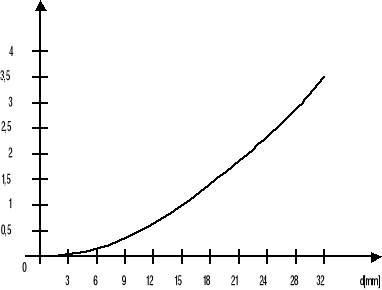
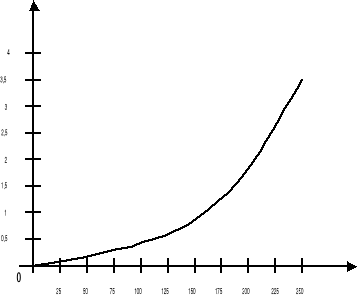
W konstrukcjach urządzeń światłowodowych szczególnym powodzeniem cieszy się zestaw dwóch soczewek: kolimująca i ogniskująca. Na bazie takiej pary skonstruowano szereg urządzeń np. sprzęgacze, tłumiki, polaryzatory itp. oraz całą gamę czujników. Zależności sprawności sprzężenia od rozseparowania pary soczewek-d, przesunięcia ich w osi-Δx, oraz od kąta nachylenia osi soczewek względem siebie przedstawiają poniższe charakterystyki.

Na bazie tych charakterystyk oraz uwzględniając właściwości soczewek (parametry), można konstruować natężeniowe czujniki przemieszczeń o zakresach pracy według potrzeb.

Następną właściwością soczewek jest transformacja położenia i kąta padania. Na poniższym rysunku przedstawiono transformację położenia i kąta padania promienia na wejściu soczewki do jej wyjścia.

0,25P 0,5P

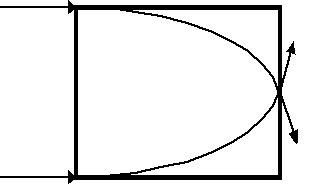
Właściwości transformacji położenia i kąta padania promienia w soczewce światłowodowej umożliwiło konstrukcję multiplekserów, demultiplekserów, sprzęgacz kierunkowych, mikrooptycznych. Jeżeli wiązkę światła wprowadzić w światłowodowy wycinek soczewki jak na poniższym rysunku, to przy odpowiednim doborze jej długości na końcu tego wycinka zaobserwuje się podział wiązki i uformowanie czterech obrazów. Efekt ten wykorzystuje się również w konstrukcji rozgałęziaczy światłowodowych.

Soczewka światłowodowa może służyć także do przenoszenia obrazu. W zależności od unormowanej długości soczewki i odległości przedmiotu od czoła soczewki można uzyskać:

a)obraz odwrócony rzeczywisty

0 <
L <  oraz ctg(
L) < n(0)
(L₁-h₁) < -tg(
L)

b)obraz prosty rzeczywisty

 < AL. < 2 oraz ctg(
L) < n(0)
(L₁-h₁) < -tg(
L)

c)obraz odwrócony urojony

/2
L < 3/2 oraz -tg(
L) < n(0)
(L₁-h₁) < ctg(
L)

d)obraz prosty urojony

AL < /2 oraz -tg(
L) < n(0)
(L₁-h₁) < ctg(
L)

Położenie przedmiotu i obrazu do czoła soczewki określa wyrażenie

przy  ≤ l
≤ 2

Tę właściwość wykorzystuje się przy konstrukcji listew obrazowodowych które znalazły zastosowanie w kopiarkach oraz czytnikach optycznych.

Jeśli soczewka światłowodowa ma optymalny profil współczynnika załamania (h₄=2/3, h₆=-17/45, itd.), to dla światła monochromatycznego promienie wychodzące z punktu x₀ przedmiotu przecinają się w punkcie mx₀ obrazu. Obraz nie ma aberracji. W rzeczywistych warunkach pracy stosuje się światło nie monochromatyczne. Wprowadzona przez strukturę soczewki dyspersja światła wywołuje aberrację chromatyczną (wada soczewek polegająca na tym że promienie o różnych barwach, wysyłane przez punktowe źródło światła, nie są zbierane w tym samym punkcie. Oznacza to że soczewka ma kilka ognisk a powstający obraz w głównym ognisku soczewki jest lekko rozmyty tzn. na brzegach plamki pojawiają się barwne obwódki wskutek rozszczepiania się światła w materiale soczewek. Do analizy aberracji chromatycznej wygodnie jest zapisać n(r) w postaci

Aberracja chromatyczna soczewki światłowodowej wynika z zależności n(0) i A od długości fali. Zależność A(λ) ma postać

Za miarę aberracji chromatycznej przyjmuje się

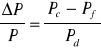
gdzie P=2/
, zaś c, f, d- określają długość fal (odpowiednio 656[nm.], 486[nm.], 589[nm.] ).

Wyrażenie to często przedstawia się w postaci:

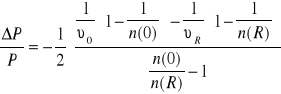
przy czym υ₀, υ_R- liczby Abbego w osi i na brzegu walca soczewki.

Odchylenie profilu n(r) soczewki gradientowej od profilu optymalnego jest również źródłem aberracji. W zastosowaniach optoelektronicznych podstawową rolę odgrywa aberracja sferyczna. Objawia się ona tym, że promienie padające równolegle na czoło soczewki mają różne punkty przecięcia z jej osią. Oprócz rozmycia ogniska aberracje uwidaczniają się w postaci zniekształcenia obrazu. Stopień aberracji określa rzeczywista wartość współczynnika h₄ opisującego aberracje najniższego rzędu. Wielkość aberracji jest proporcjonalna do różnicy (h₄-2/3), a w formie zniekształcenia obrazu (typu poduszka, beczka) zależą od parametrów konkretnej soczewki.

L

F₁

F₂

L₁

L₂

P₁

P₂

S₁

S₂

h₂

h₁

Światłowód

Soczewka

Źródło

NA_WE

NA_WY

l₁

L

l₂

NA_Wy

NA_WE

λ=0,83[m.]

λ=0,63[m.]

Δx[μm.]

[dB]

[dB]

[dB]

ϕ[mrad]

---