Spis treści:
Wstęp
Sprawozdanie zostało podzielone na poszczególne części:
Opracowanie danych źródłowych.
Opracowanie szeregów rozdzielczych liczebności.
Wykresy.
Wnioski.
Dane pomiarowe
Do wykonania ćwiczenia otrzymaliśmy od prowadzącego dane źródłowe wraz z
odpowiednimi wytycznymi dotyczącymi zmiennej skokowej oraz ciągłej - będące załącznikiem na początku sprawozdania.
Zmienna skokowa
Po zastosowaniu wszystkich wytycznych dotyczących danych źródłowych, liczby zawarte w poniższej tabeli (TABELA 1) przedstawiają liczbę samochodów przejeżdżających przez przekrój drogi w jednakowych odstępach czasowych - zmienna skokowa.
Tabela 1 - Liczba pojazdów przejeżdżających przez przekrój drogi w jednakowych odstępach czasowych
10 |
14 |
17 |
1 |
11 |
9 |
11 |
6 |
15 |
14 |
17 |
21 |
11 |
19 |
15 |
16 |
2 |
11 |
14 |
8 |
11 |
15 |
12 |
16 |
20 |
11 |
14 |
8 |
16 |
8 |
20 |
20 |
5 |
8 |
20 |
16 |
12 |
8 |
3 |
6 |
5 |
8 |
4 |
6 |
7 |
11 |
5 |
8 |
5 |
4 |
0 |
2 |
7 |
9 |
20 |
8 |
20 |
11 |
20 |
8 |
8 |
9 |
3 |
15 |
9 |
29 |
8 |
8 |
9 |
2 |
5 |
6 |
33 |
11 |
5 |
7 |
21 |
9 |
6 |
9 |
11 |
26 |
15 |
24 |
29 |
4 |
29 |
23 |
7 |
4 |
23 |
6 |
4 |
6 |
23 |
3 |
4 |
3 |
5 |
26 |
10 |
9 |
18 |
15 |
32 |
11 |
2 |
10 |
9 |
26 |
6 |
6 |
16 |
3 |
26 |
20 |
15 |
9 |
17 |
17 |
3 |
2 |
3 |
5 |
1 |
8 |
13 |
5 |
4 |
8 |
12 |
12 |
17 |
0 |
5 |
4 |
8 |
1 |
3 |
1 |
3 |
13 |
6 |
4 |
9 |
29 |
23 |
27 |
18 |
20 |
23 |
9 |
2 |
23 |
29 |
6 |
8 |
13 |
10 |
4 |
7 |
12 |
2 |
2 |
8 |
13 |
10 |
4 |
22 |
3 |
4 |
2 |
16 |
16 |
17 |
17 |
17 |
18 |
25 |
22 |
28 |
30 |
14 |
18 |
25 |
18 |
19 |
29 |
31 |
30 |
32 |
26 |
24 |
2 |
1 |
29 |
23 |
22 |
32 |
19 |
14 |
23 |
28 |
28 |
25 |
12 |
21 |
25 |
25 |
23 |
30 |
1 |
24 |
0 |
0 |
2 |
25 |
29 |
18 |
19 |
15 |
12 |
32 |
13 |
24 |
27 |
3 |
31 |
2 |
26 |
30 |
28 |
16 |
16 |
20 |
21 |
22 |
19 |
33 |
39 |
35 |
40 |
38 |
37 |
37 |
40 |
40 |
36 |
35 |
35 |
38 |
37 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
* 1 Źródło: dane otrzymane od prowadzącego po zastosowaniu wytycznych
Po odpowiednim uporządkowaniu (według wartości rosnących) danych w tabeli Tabeli 1, utworzyliśmy Tabelę 2.
Tabela 2 - Liczba pojazdów przejeżdżających przez przekrój drogi w jednakowych odstępach czasowych według wartości rosnących
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
7 |
7 |
7 |
7 |
7 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
10 |
10 |
10 |
10 |
10 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
13 |
13 |
13 |
13 |
13 |
14 |
14 |
14 |
14 |
14 |
14 |
15 |
15 |
15 |
15 |
15 |
15 |
15 |
15 |
16 |
16 |
16 |
16 |
16 |
16 |
16 |
16 |
16 |
17 |
17 |
17 |
17 |
17 |
17 |
17 |
17 |
18 |
18 |
18 |
18 |
18 |
18 |
19 |
19 |
19 |
19 |
19 |
20 |
20 |
20 |
20 |
20 |
20 |
20 |
20 |
20 |
20 |
21 |
21 |
21 |
21 |
22 |
22 |
22 |
22 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
24 |
24 |
24 |
24 |
25 |
25 |
25 |
25 |
25 |
25 |
26 |
26 |
26 |
26 |
26 |
26 |
27 |
27 |
28 |
28 |
28 |
28 |
29 |
29 |
29 |
29 |
29 |
29 |
29 |
29 |
30 |
30 |
30 |
30 |
31 |
31 |
32 |
32 |
32 |
32 |
33 |
33 |
35 |
35 |
35 |
36 |
37 |
37 |
37 |
38 |
38 |
39 |
40 |
40 |
40 |
|
|
|
* 2 Źródło: Tabela 1
Dane w Tabeli 2 tworzą szereg statystyczny.
Obie powyższe tabele czytamy poziomo-wierszami.
Zmienna ciągła
Po zastosowaniu wszystkich wytycznych dotyczących danych źródłowych, liczby zawarte w poniższej tabeli (TABELA 3) przedstawiają wartości odstępów czasowych pomiędzy samochodami w minutach na drodze lokalnej zamiejskiej - zmienna ciągła.
Tabela 3 - wartości odstępów czasowych pomiędzy samochodami w minutach na drodze lokalnej zamiejskiej
10 |
15 |
14 |
17 |
1 |
11 |
9 |
11 |
6 |
15 |
14 |
17 |
21 |
11 |
15 |
12 |
16 |
2 |
11 |
14 |
21 |
20 |
11 |
14 |
8 |
11 |
11 |
19 |
16 |
12 |
12 |
20 |
20 |
5 |
21 |
20 |
16 |
12 |
3 |
6 |
5 |
8 |
4 |
13 |
6 |
7 |
9 |
5 |
29 |
5 |
4 |
0 |
7 |
9 |
20 |
8 |
9 |
23 |
9 |
20 |
18 |
29 |
20 |
1 |
29 |
8 |
8 |
9 |
2 |
5 |
9 |
7 |
6 |
9 |
11 |
5 |
23 |
9 |
23 |
9 |
11 |
26 |
15 |
24 |
29 |
2 |
4 |
29 |
23 |
7 |
7 |
6 |
7 |
6 |
23 |
3 |
4 |
33 |
5 |
5 |
26 |
10 |
9 |
18 |
13 |
11 |
8 |
10 |
9 |
26 |
6 |
6 |
16 |
7 |
3 |
26 |
20 |
15 |
20 |
17 |
17 |
2 |
15 |
5 |
1 |
8 |
13 |
4 |
5 |
4 |
18 |
12 |
13 |
0 |
4 |
4 |
8 |
1 |
17 |
1 |
6 |
5 |
13 |
6 |
4 |
9 |
14 |
29 |
29 |
20 |
23 |
9 |
2 |
23 |
29 |
6 |
12 |
13 |
10 |
4 |
12 |
2 |
2 |
13 |
10 |
4 |
3 |
3 |
22 |
9 |
14 |
4 |
2 |
16 |
17 |
17 |
17 |
25 |
22 |
28 |
21 |
23 |
9 |
14 |
18 |
25 |
18 |
19 |
31 |
30 |
32 |
24 |
2 |
1 |
23 |
27 |
23 |
22 |
32 |
19 |
14 |
23 |
25 |
25 |
23 |
32 |
30 |
17 |
29 |
1 |
30 |
1 |
24 |
0 |
0 |
2 |
25 |
29 |
18 |
19 |
15 |
12 |
32 |
13 |
24 |
27 |
14 |
31 |
2 |
26 |
30 |
28 |
16 |
16 |
20 |
21 |
22 |
19 |
33 |
39 |
35 |
40 |
38 |
37 |
37 |
40 |
40 |
36 |
35 |
35 |
38 |
37 |
* 3 Źródło: dane otrzymane od prowadzącego po zastosowaniu wytycznych
Po odpowiednim uporządkowaniu (według wartości rosnących) danych w tabeli Tabeli 3, utworzyliśmy Tabelę 4.
Tabela 4 - wartości odstępów czasowych pomiędzy samochodami w minutach na drodze lokalnej zamiejskiej według wartości rosnących
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
10 |
10 |
10 |
10 |
10 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
13 |
13 |
13 |
13 |
13 |
13 |
13 |
13 |
14 |
14 |
14 |
14 |
14 |
14 |
14 |
14 |
14 |
15 |
15 |
15 |
15 |
15 |
15 |
15 |
16 |
16 |
16 |
16 |
16 |
16 |
16 |
17 |
17 |
17 |
17 |
17 |
17 |
17 |
17 |
17 |
18 |
18 |
18 |
18 |
18 |
18 |
19 |
19 |
19 |
19 |
19 |
20 |
20 |
20 |
20 |
20 |
20 |
20 |
20 |
20 |
20 |
20 |
21 |
21 |
21 |
21 |
21 |
22 |
22 |
22 |
22 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
24 |
24 |
24 |
24 |
25 |
25 |
25 |
25 |
25 |
26 |
26 |
26 |
26 |
26 |
27 |
27 |
28 |
28 |
29 |
29 |
29 |
29 |
29 |
29 |
29 |
29 |
29 |
29 |
30 |
30 |
30 |
30 |
31 |
31 |
32 |
32 |
32 |
32 |
33 |
33 |
25 |
35 |
35 |
36 |
37 |
37 |
37 |
38 |
38 |
39 |
40 |
40 |
40 |
|
|
|
|
* 4 Źródło: Tabela 3
Dane w Tabeli 2 tworzą szereg statystyczny.
Obie powyższe tabele czytamy poziomo-wierszami.
2.1 Porządkowanie i grupowanie danych
Chcąc utworzyć szeregi rozdzielcze dla danych podanych w Tabelach 1 i 3, musimy porównać cechy danych zawartych w w/w zbiorach.
Zmienna skokowa:
Wartość maksymalna Xmax:40
Wartość minimalna Xmin:0
Zmienna ciągła:
Wartość maksymalna Xmax:40
Wartość minimalna Xmin:0
Dla zmiennej ciągłej i skokowej wartości minimalne i maksymalne są takie same.
Dlatego dla obydwu zmiennych tworząc empiryczny obszar zmienności (litera R) bierzemy te same wartości Xmax:40, Xmin:0.
R= Xmax- Xmin
Poniższa Tabela 5 została utworzona na podstawie równania empirycznego obszaru zmienności w materiale danych.
R=c×h (równanie 1)
c - liczba przedziałów klasowych
h - długość przedziału klasowego
Tabela 5 - Długość przedziałów klasowych i ich liczba dla rozstępu R=40
Lp. |
Przedziały klasowe |
Lp. |
Przedziały klasowe |
Lp. |
Przedziały klasowe |
|||
|
c |
h |
|
c |
h |
|
c |
h |
1 |
1 |
40 |
15 |
15 |
2,(6) |
29 |
29 |
1,37 |
2 |
2 |
20 |
16 |
16 |
2,5 |
30 |
30 |
1,(3) |
3 |
3 |
13,(3) |
17 |
17 |
2,3 |
31 |
31 |
1,29 |
4 |
4 |
10 |
18 |
18 |
2,(2) |
32 |
32 |
1,25 |
5 |
5 |
8 |
19 |
19 |
2,1 |
33 |
33 |
1,21 |
6 |
6 |
6,(6) |
20 |
20 |
2 |
34 |
34 |
1,17 |
7 |
7 |
5,7 |
21 |
21 |
1,9 |
35 |
35 |
1,14 |
8 |
8 |
5 |
22 |
22 |
1,8 |
36 |
36 |
1,11 |
9 |
9 |
4,(4) |
23 |
23 |
1,7 |
37 |
37 |
1,08 |
10 |
10 |
4 |
24 |
24 |
1,(6) |
38 |
38 |
1,05 |
11 |
11 |
3,6 |
25 |
25 |
1,6 |
39 |
39 |
1,02 |
12 |
12 |
3,(3) |
26 |
26 |
1,53 |
40 |
40 |
1 |
13 |
13 |
3,1 |
27 |
27 |
1,48 |
|
|
|
14 |
14 |
2,8 |
28 |
28 |
1,42 |
|
|
|
* 5 Źródło: dane otrzymane od prowadzącego
2.2 Zmienna skokowa
Po opracowaniu Tabeli 2, sporządzony zostaje szereg liczebności pojazdów samochodowych (Tabela 6).
Tabela 6 - Szereg liczebności pojazdów samochodowych
Liczba pojazdów [xi] |
Liczebność [ni] |
Liczba pojazdów [xi] |
Liczebność [ni] |
0 |
4 |
21 |
4 |
1 |
7 |
22 |
4 |
2 |
12 |
23 |
9 |
3 |
11 |
24 |
4 |
4 |
12 |
25 |
6 |
5 |
10 |
26 |
6 |
6 |
11 |
27 |
2 |
7 |
5 |
28 |
4 |
8 |
17 |
29 |
8 |
9 |
12 |
30 |
4 |
10 |
5 |
31 |
2 |
11 |
11 |
32 |
4 |
12 |
7 |
33 |
2 |
13 |
5 |
34 |
0 |
14 |
6 |
35 |
3 |
15 |
8 |
36 |
1 |
16 |
9 |
37 |
3 |
17 |
8 |
38 |
2 |
18 |
6 |
39 |
1 |
19 |
5 |
40 |
3 |
20 |
10 |
|
|
Suma: |
253 |
||
* 6 Źródło: Tabela 2
Na podstawie Tabeli 6 stworzone zostało 5 wariantów szeregów rozdzielczych ze zmienianymi wartościami, c (liczba przedziałów klasowych) i h (długość przedziału klasowego).
Tabela 7 - Szereg rozdzielczy zmienna skokowa WARIANT I || c=11, h=8
Numer przedziału klasowego |
Liczba pojazdów x0i - x1i |
Liczebność ni |
1 |
0-3 |
34 |
2 |
4-7 |
38 |
3 |
8-11 |
45 |
4 |
12-15 |
26 |
5 |
16-19 |
28 |
6 |
20-24 |
31 |
7 |
25-27 |
14 |
8 |
28-31 |
18 |
9 |
32-35 |
9 |
10 |
36-40 |
10 |
Razem: |
253 |
|
* 7 Źródło: Tabela 6
Tabela 8 - Szereg rozdzielczy zmienna skokowa WARIANT II || c=8, h=4
Numer przedziału klasowego |
Liczba pojazdów x0i - x1i |
Liczebność ni |
1 |
0-4 |
46 |
2 |
5-9 |
55 |
3 |
10-14 |
34 |
4 |
15-19 |
36 |
5 |
20-24 |
31 |
6 |
25-29 |
26 |
7 |
30-34 |
12 |
8 |
35-40 |
13 |
Razem: |
253 |
|
* 8 Źródło: Tabela 6
Tabela 9 - Szereg rozdzielczy zmienna skokowa WARIANT III || c=5, h=7
Numer przedziału klasowego |
Liczba pojazdów x0i - x1i |
Liczebność ni |
1 |
0-7 |
72 |
2 |
8-15 |
71 |
3 |
16-23 |
55 |
4 |
24-31 |
36 |
5 |
32-40 |
19 |
Razem: |
253 |
|
* 9 Źródło: Tabela 6
Tabela 10 - Szereg rozdzielczy zmienna skokowa WARIANT IV || c=14, h=2
Numer przedziału klasowego |
Liczba pojazdów x0i - x1i |
Liczebność ni |
1 |
0-2 |
23 |
2 |
3-5 |
33 |
3 |
6-8 |
33 |
4 |
9-11 |
28 |
5 |
12-14 |
18 |
6 |
15-17 |
25 |
7 |
18-20 |
21 |
8 |
21-23 |
17 |
9 |
24-26 |
16 |
10 |
27-29 |
14 |
11 |
30-32 |
10 |
12 |
33-35 |
5 |
13 |
36-38 |
6 |
14 |
39-40 |
4 |
Razem: |
253 |
|
* 10 Źródło: Tabela 6
Tabela 11 - Szereg rozdzielczy zmienna skokowa WARIANT V || c=6, h=6
Numer przedziału klasowego |
Liczba pojazdów x0i - x1i |
Liczebność ni |
1 |
0-6 |
67 |
2 |
7-13 |
62 |
3 |
14-20 |
52 |
4 |
21-27 |
35 |
5 |
28-34 |
24 |
6 |
35-40 |
13 |
Razem: |
253 |
|
* 11 Źródło: Tabela 6
Z przedstawionych w Tabelach 7-11 wariantów szeregów rozdzielczych zmiennej skokowej został wybrany jeden. Najodpowiedniejszy okazał się WARIANT II, przedstawiony w Tabeli 8.
Podczas dokonywania wyboru wzięto pod uwagę sugestie prowadzącego, oraz następujące wytyczne:
Klasy obejmują wszystkie dane zawarte w Tabeli 1.
Ilość przedziałów klasowych zawarta jest w przedziale od 6 do 15.
Ustalenie jednakowych granic przedziałów klasowych.
Długość przedziału jest liczbą prostą.
Tabela 12 - Wybrany szereg rozdzielczy || c=8, h=4 + rozkład procentowy
Numer przedziału klasowego |
Liczba pojazdów x0i - x1i |
Liczebność ni |
Rozkład procentowy |
1 |
0-4 |
46 |
18,18% |
2 |
5-9 |
55 |
21,74% |
3 |
10-14 |
34 |
13,44% |
4 |
15-19 |
36 |
14,23% |
5 |
20-24 |
31 |
12,25% |
6 |
25-29 |
26 |
10,28% |
7 |
30-34 |
12 |
4,74% |
8 |
35-40 |
13 |
5,14% |
Razem: |
253 |
100% |
|
* 12 Źródło: Tabela 8
Poniższa Tabela 14 przedstawia szereg kumulacyjny, utworzony na podstawie wybranego szeregu rozdzielczego.
Tabela 13 - Kumulacyjny rozkład liczebności zmienna skokowa
Lp. |
Liczba pojazdów |
Frekwencja skumulowana nsk |
Rozkład procentowy |
1 |
mniej niż 4 |
46 |
18,18% |
2 |
mniej niż 9 |
101 |
39,92% |
3 |
mniej niż 14 |
135 |
53,35% |
4 |
mniej niż 19 |
171 |
67,58% |
5 |
mniej niż 24 |
202 |
79,84% |
6 |
mniej niż 29 |
228 |
90,11% |
7 |
mniej niż 34 |
240 |
94,86% |
8 |
mniej niż 40 |
253 |
100% |
* 13 Źródło: Tabela 12
Z tabeli numer 12 wynika, iż dominujące przedziały liczby pojazdów zaobserwowanych w jednakowych przedziałach pomiarowych są następujące:
0-4
5-9
15-19
Aby lepiej wyrazić te proporcje utworzyć należy kolejną tabelę częstości względnych i poziomów dystrybuant empirycznych dla zmiennej skokowej należy posłużyć się równaniem,
![]()
ni — liczebność (frekwencja ) przedziału klasowego
n — liczba pomiarów
oraz definicją dystrybuanty empirycznej - jest to częstość względna dla wszystkich wariantów cechy mniejszych od przyjętej wartości.
Tabela 14 - Częstości względne i poziomy dystrybuant empirycznych
Numer przedziału klasowego |
Liczba pojazdów x0i - x1i |
Liczebność ni |
Częstotliwość względna wi |
Poziomy dystrybuant empirycznych W (x< xi) |
1 |
0-4 |
46 |
0,18 |
0,18 |
2 |
5-9 |
55 |
0,22 |
0,40 |
3 |
10-14 |
34 |
0,14 |
0,54 |
4 |
15-19 |
36 |
0,14 |
0,68 |
5 |
20-24 |
31 |
0,12 |
0,80 |
6 |
25-29 |
26 |
0,10 |
0,90 |
7 |
30-34 |
12 |
0,05 |
0,95 |
8 |
35-40 |
13 |
0,05 |
1 |
Razem: |
253 |
1 |
# |
|
* 14 Źródło: Tabela 12
Aby bardziej szczegółowo zobrazować frekwencje przedziałów klasowych, przydzielono im różne rozpiętości. Bierzemy pod uwagę największy rozkład procentowy danych klas.
Tabela 15 - Szereg rozdzielczy z różnymi rozpiętościami przedziałów klasowych
Numer przedziału klasowego |
Przedziały częściowe dotyczące liczby pojazdów x0i - x1i |
Liczebność ni |
1 |
0-2 |
23 |
2 |
3-5 |
33 |
3 |
6-7 |
16 |
4 |
8-10 |
34 |
5 |
11-13 |
23 |
6 |
14-15 |
14 |
7 |
16-17 |
17 |
8 |
18-20 |
21 |
9 |
21-25 |
27 |
10 |
26-30 |
26 |
11 |
31-35 |
11 |
12 |
36-40 |
10 |
Razem: |
253 |
|
* 15 Źródło: na postawie Tabeli 12
W przypadku kiedy mamy do czynienia z szeregiem rozdzielczym o różnych rozpiętościach przedziałów klasowych możemy utworzyć tabele wskaźników gęstości i natężenia liczebności.
Korzystamy w tym przypadku z następujących definicji:
Wskaźnik gęstości jest miarą stosowaną w przypadku, gdy rozpiętość przedziałów klasowych nie są równe. Jest definiowany jako stosunek liczebości w poszczególnych klasach szeregu do rozpiętości przedziału hi i określa, ile jednostek zbiorowości przypada na jednostkę wartości zmiennej w każdej klasie.
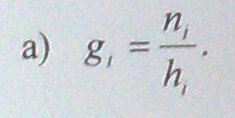
Wskaźnik natężenia liczebności otrzymuje się przez przeliczenie wszystkich liczebności na jedną rozpiętość przedziału. Określa on częstość występowania jednostek zbiorowości na jednakową rozpiętość przedziału klasowego w danym szeregu i obliczany jest według wzoru:
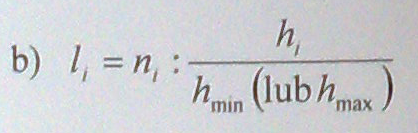
W literaturze frekwencja nazywana jest niekiedy częstością [1]
Politechnika Śląska Studia niestacjonarne
„Analiza struktury danych pomiarowych”
Kwiatek Dawid
Strona 12
Wyszukiwarka