WYKŁAD 4:

BADANIE STABILNOŚCI LINIOWYCH UKŁADÓW STEROWANIA

OCENA USTALONYCH UCHYBÓW STEROWANIA
SYNTEZA W OPARCIU O TRANSMITANCJE WZORCOWE

1 Stabilność

1.1 Modele wejściowo-wyjściowe: stabilność w sensie BIBO

Układ opisywany transmitancją

jest układem stabilnym w sensie BIBO (Bounded-Input-Bounded-Output), gdy

każdemu ograniczonemu wejściu odpowiada ograniczone wyjście.

'Ograniczoność' dotyczy amplitudy (wartości maksymalnej) danego sygnału.

Warunek BIBO-stabilności:

wszystkie bieguny transmitancji
muszą leżeć w lewej otwartej półpłaszczyźnie

płaszczyzny zespolonej, to znaczy: części rzeczywiste wszystkich biegunów muszą być

ujemne.

1.2 Modele wejściowo-wyjściowe: wewnętrzna stabilność

Uogólnienie stabilności w sensie BIBO:

człony dynamiczne opisywane są modelami wejściowo-wyjściowymi (transmitancjami),

ale pod uwagę bierze się także strukturę układu.

Układ jest wewnętrznie stabilny (internally stable), gdy jest BIBO-stabilny dla każdej,

pary wejście-wyjście, możliwej do wyróżnienia w tym układzie.

1.3 Modele w przestrzeni stanu: asymptotyczna stabilność

Model:

Układ jest asymptotycznie stabilny wtedy i tylko wtedy, gdy dla dowolnych warunków

początkowych
przy zerowym pobudzeniu
zachodzi

.

Przypominamy, iż

gdzie
,

,

macierz jednostkowa.

Układ jest asymptotycznie stabilny wtedy i tylko wtedy, gdy wszystkie wartości własne

macierzy stanu
leżą w lewej otwartej półpłaszczyźnie płaszczyzny zespolonej.

Wartości własne kwadratowej macierzy
to pierwiastki równania charakterystycznego

tej macierzy

,
macierz jednostkowa.

Zachodzi przy tym

asymptotyczna stabilność
wewnętrzna stabilność
stabilność w sensie BIBO .

W praktyce poszukuje się pośrednich kryteriów badana stabilności.

Najpopularniejsze dla BIBO-stabilności jest kryterium tablicowe Routha-Hurwitza.

2 Dokładność

2.1 Podstawowe pojęcia

Dokładność układu sterowania rozumiemy jako dokładność w stanie ustalonym.

O dokładności takiej orzeka się zatem, analizując ustalona wartość uchybu sterowania.

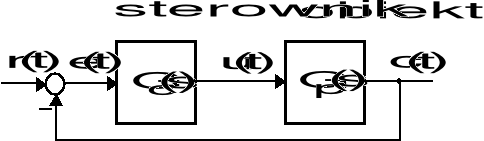
Podstawowy strukturalny schemat układu sterowania

- transmitancja sterowanego obiektu,

- transmitancja sterownika.

Uchyb sterowania (uchyb systemowy) definiuje się jako:

, (
- transformata Laplace'a),

gdzie

- wielkość zadana (
- transformata Laplace'a),

- wielkość sterowana (
- transformata Laplace'a)

oraz

- sygnał sterujący (
- transformata Laplace'a)

Na podstawie powyższego rysunku łatwo zapisać następujące sygnałowe relacje:

,

,

.

Stąd

,

a zatem

,

.

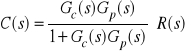
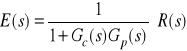
Wprowadza się transmitancje, opisujące podstawowe własności układu zamkniętego:

- sygnałowa transmitancja:

,

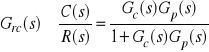
- sygnałowa transmitancja uchybowa:

.

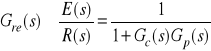
Jak łatwo zauważyć transmitancje te stanowią komplementarną parę:

.

Źródłem uchybu mogą być zakłócenia, oddziałujące na sterowany obiekt (układ):

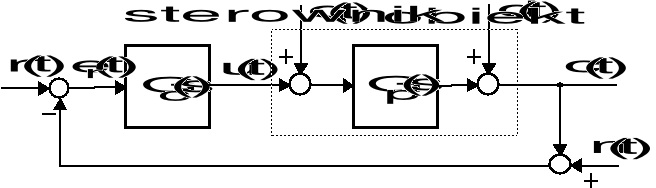
Strukturalny schemat układu sterowania

Mamy teraz:

- zakłócenie na wyjściu obiektu (
- transformata Laplace'a),

- zakłócenie na wyjściu obiektu (
- transformata Laplace'a),

- szum pomiarowy (
- transformata Laplace'a),

- sygnał różnicowy (
- transformata Laplace'a).

Uwaga:

- w ogólności uchyb sterowania (
) jest zatem

różny od sygnału różnicowego, 'rzeczywiście' stosowanego do

wypracowania sygnału sterującego obiektem!

Zachodzi (proszę sprawdzić):

,
,

,

,
.

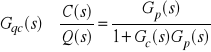
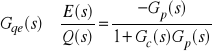
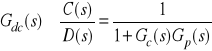
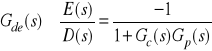
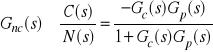
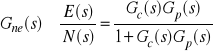
Uwaga:

Transmitancje
,
oraz
to zakłóceniowe transmitancje uchybowe.

We wszystkich transmitancjach w mianowniku występuje wyrażenie
. Układ sterowania jest zatem stabilny w sensie BIBO, gdy wszystkie pierwiastki równania
leżą w lewej otwartej półpłaszczyźnie plaszczyzny zespolonej.

2.2 Błąd w stanie ustalonym

Aby sensownie mówić o stanie ustalonym, należy zapewnić układowi sterowania stabilność, przynajmniej w sensie stabilności wewnętrznej.

Zakłada się zatem, że układ sterowania jest stabilny w sensie stabilności wewnętrznej.

Transformata uchybu dla wielkości zadającej
:

.

Ustaloną wartość
uchybu
uzyskuje się zatem ze wzoru

.

Transformata uchybu dla (przykładowego) zakłócenia
:

.

Ustalona wartość
uchybu
wynika zatem ze wzoru

.

2.3 Błędy położeniowe

W praktyce szczególne znaczenie posiadają oszacowania ustalonych błędów dla specyficznych, prototypowych jednostkowych sygnałów zadających:

sygnału położeniowego, prędkościowego oraz parabolicznego.

Dla pobudzenia położeniowego mamy:

,
.

Zachodzi zatem

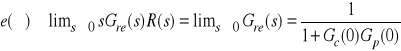
Uchyb ten będzie zatem:

skończony lecz niezerowy, gdy

(w praktyce:  lub ),

skończony i zerowy, gdy

(w praktyce: ).

Wielkość

nazywana jest statycznym wzmocnieniem otwartego układu sterowania.

W rozważanym przypadku zachodzi zatem

.

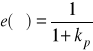
Zauważmy skończona wartość
oznacza, iż transmitancja
otwartego układu sterowania, definiowana jako

,

nie posiada biegunów w zerze, to znaczy
.

Układ sterowania (stabilny!) o skończonym statycznym wzmocnieniu
nazywamy układem statycznym lub układem o zerowym astatyzmie (układem typu '0').

2.4 Błędy prędkościowe

Dla pobudzenia prędkościowego ('pobudzenie typu 'rampa') mamy:

,
.

Zauważmy, że jest to pobudzenie nieskończenie narastające w czasie.

Zachodzi przeto

.

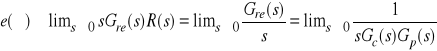
Wielkość

nazywa się prędkościowym wzmocnieniem układu sterowania.

W rozważanym przypadku mamy zatem

.

Możliwe są następujące sytuacje:

uchyb jest nieskończny
, gdy

(w praktyce: ),

uchyb ma wartość skończoną, lecz niezerową, gdy

(w praktyce: ),

uchyb ma wartość skończoną i zerową, gdy

(w praktyce: ).

Układ o skończonym lecz niezerowym prędkościowym wzmocnieniu
nazywany jest układem o astatyzmie pierwszego rzędu (układem typu '1').

Transmitancja otwartej pętli
układu sterowania o astatyzmie pierwszego rzędu posiada zatem pojedynczy biegun w zerze.

Układ o zerowym stopniu astatyzmu charakteryzuje się zerowym wzmocnieniem prędkościowym
.

2.5 Błędy przyspieszeniowe

Dla pobudzenia przyspieszeniowego ('pobudzenie typu 'parabola') mamy:

,
.

Jest to zatem pobudzenie nieskończenie narastające w czasie. Zachodzi przeto

.

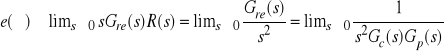
Wielkość

nazywa się przyspieszeniowym wzmocnieniem układu sterowania.

W rozważanym przypadku mamy zatem

.

Wyróżnić można następujące sytuacje:

uchyb jest nieskończny
, gdy

(w praktyce: ),

uchyb ma wartość skończoną, lecz niezerową, gdy

(w praktyce: ),

uchyb ma wartość skończoną i zerową, gdy

(w praktyce: ).

Układ o skończonym lecz niezerowym przyspieszeniowym wzmocnieniu
nazywany jest układem o astatyzmie drugiego rzędu (układem typu '2').

Transmitancja otwartej pętli
układu sterowania o astatyzmie drugiego rzędu posiada zatem podwójny biegun w zerze.

Układ o stopniu astatyzmu 0 lub 1 charakteryzuje się zerowym wzmocnieniem przyspieszniowym
.

2.6 Podsumowanie

Układ typu	0	1	2
Wzmocnienie
Wzmocnienie	0
Wzmocnienie	0	0
Błąd dla		0	0
Błąd dla			0
Błąd dla

3 Synteza układu sterowania w oparciu o prototypową transmitancję

układu zamkniętego

Jest to bardzo prosta metoda projektowania struktury oraz parametrów sterownika dla zadanej postaci transmitancji zamkniętego układu sterowania.

Transmitancja taka, zwykle jest to transmitancja drugiego rzędu nazywana jest transmitancją prototypowa (wzorcową). Transmitancję tę wyznacza się w oparciu o projektowe wymagania (specyfikacje), określające pożadane cechy układu zamkniętego, a więc charakterystyki stabilnościowe, dokładnościowe oraz szybkościowe tego układu.

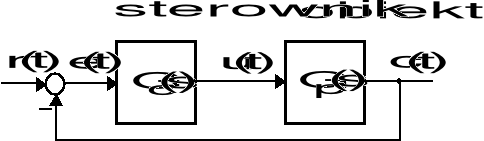
Podstawowy strukturalny schemat układu sterowania

Gdzie

- znana transmitancja sterowanego obiektu,

- projektowana transmitancja sterownika.

Sygnałowa transmitancja układu zamkniętego:

.

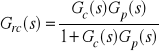
Transmitancja wzorcowa (oczywiście żąda się w tym miejscu transmitancji BIBO-stabilnych)

.

Transmitancję sterownika wyznacza się zatem z równania

,

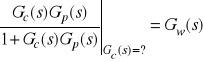
a zatem

.

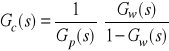
Z powyższego wynika, iż tak zaprojektowany sterownik musi całowicie 'skompensować' dynamiczne działanie sterowanego obiektu (w transmitancji sterownika występuje odwracanie transmitancji obiektu). Takie postępowanie, przede wszystkim ze względu na wewnętrzną stabilność projektowanego układu, w praktyce napotyka szereg ograniczeń - nadaje się zatem tylko do syntezy bardzo prostych układów sterowania (np. prostych układów napędowych).

W dalszych przykładach przyjmujemy elementarną postać wzorcowej transmitancji drugiego rzędu

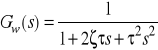
której parametry
oraz
wyznacza się na podstawie wymagań, dotyczących stabilności (co można związać np. z przeregulowaniem
odpowiedzi skokowej), szybkości (czemu przyporządkować można czasy maksimum
i/lub ustalania
tej odpowiedzi) oraz dokładności sterowania (najczęściej stosuje się tu wymaganie, odniesione do prędkościowego wzmocnienia
).

Przykład 1 (kryterium Routha-Hurwitza)

Na podstawie kryterium Routha-Hurwitza, określ liczbę pierwiastków następującego równania

. (1)

Rozwiązanie

Tablica Routha, odpowiadająca równaniu (1), ma postać daną wzorem

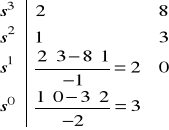
(2)

Ponieważ w pierwszej kolumnie owej tablicy nie występuje zmiana znaku, wszystkie pierwiastki rozważanego równania leżą w lewej półpłaszczyźnie.

Przykład 2 (kryterium Routha-Hurwitza)

Na podstawie kryterium Routha-Hurwitza, określ liczbę pierwiastków następującego równania

, (1)

leżących w prawej półpłaszczyźnie płaszczyzny zespolonej.

Rozwiązanie

Tablica Routha, odpowiadająca równaniu (1), ma postać daną wzorem

(2)

W tablicy tej występuje wiersz złożony tylko z zerowych elementów (wiersz ten odpowiada nieparzystej trzeciej potędze zmiennej zespolonej s). W takim przypadku zerowy wiersz tablicy zastąpić należy wierszem utworzonym ze współczynników zróżniczkowanego pomocniczego wielomianu
, który tworzy się w oparciu wiersz bezpośrednio poprzedzający rozważany zerowy wiersz. Zgodnie z kryterium Routha-Hurwitza, pomocniczy wielomian ma postać
, a zatem elementy wiersza zastępującego zerowy wiersz tablicy (5.2) oblicza się w następujący sposób:
. Po dokonaniu odpowiedniej zamiany, wypełnianie tablicy Routha jest kontynuowane. Analiza liczby zmian znaku elementów pierwszej kolumny tej tablicy wskazuje, iż równanie (1) ma dwa pierwiastki leżące w prawej półpłaszczyźnie płaszczyzny zespolonej. Pomocniczy wielomian
, wykorzystywany przy opisanej rekonstrukcji elementów zerowego wiersza tablicy Routha, jest zawsze wielomianem, w którym zespolona zmienna s występuje tylko w parzystych potęgach. Oznacza to, że pierwiastki tego pomocniczego wielomianu, będące także pierwiastkami "pierwotnego" wielomianu
, rozmieszczone są na płaszczyźnie zespolonej symetrycznie względem osi urojonej. Pierwiastki takie mogą zatem występować w parach (pierwiastki rzeczywiste lub urojone), bądź też w kwartetach (dwie pary pierwiastków sprzężonych zespolonych o niezerowych częściach rzeczywistych).

Przykład 3 (kryterium Routha-Hurwitza)

Równanie charakterystyczne pewnego układu dynamicznego ma postać daną wzorem

. (1)

Stosując kryterium Routha-Hurwitza, zbadaj liczbę pierwiastków tego równania, leżących w prawej półpłaszczyźnie płaszczyzny zespolonej.

Rozwiązanie

Tablica Routha przedstawia się tu następująco

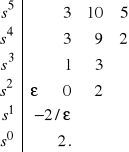
(2)

W tablicy tej wystąpił niezerowy wiersz (odpowiadający drugiej potędze zespolonej zmiennej s) o zerowym pierwszym elemencie. W takim przypadku element ów zastąpić należy "małą" dodatnią liczbą
i kontynuować obliczenia w celu określenia wartości dalszych elementów tablicy (niektóre z tych elementów będą teraz funkcjami parametru
). Z bilansu liczby zmian znaku elementów pierwszej kolumny tak uzyskanej tablicy Routha wynika liczba pierwiastków równania
, które leżą w prawej półpłaszczyźnie płaszczyzny zespolonej. Ze wzoru (2) wnioskujemy zatem, iż rozważane równanie
posiada dwa takie pierwiastki.

Przykład 4 (stabilność wewnętrzna)

Dany jest układ sterowania o strukturalnym schemacie jak na rysunku danym niżej.

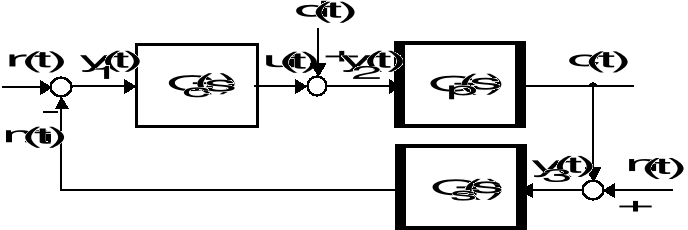
Strukturalny schemat układu sterowania

Operatorowe transmitancje
,
oraz
oznaczają tu odpowiednio: transmitancję sterowanego obiektu, transmitancję sterownika oraz transmitancję pomiarowego czujnika. Zachodzi przy tym

,
oraz
. (1)

Sygnały dochodzące do sumacyjnych węzłów tego schematu oznaczają:
- sygnał wielkości sterowanej,
- sygnał wielkości zadającej,
- sygnał sterujący,
- sygnał pomiarowy,
- zakłócenie oddziałujące na wejście sterowanego obiektu oraz
- szum pomiarowy. Zbadaj czy rozważany układ sterowania jest dobrze określony oraz wewnetrznie (totalnie) stabilny.

Rozwiązanie

Oznaczmy przez
,
oraz
transformaty sygnałów wychodzących z odpowiednich sumacyjnych węzłów rozważanego schematu. Zgodnie z rysunkiem zachodzi zatem

, (2)

, (3)

. (4)

Zapisując powyższe wzory w macierzowej postaci, otrzymujemy

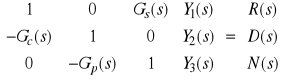
. (5)

Aby układ sterowania był dobrze określony, muszą istnieć wszystkie operatorowe transmitancje zdefiniowane dla trójki zewnętrznych sygnałów
oraz trójki wyróżnionych wewnętrznych sygnałów
tego układu. Warunek dobrej określoności rozpatrywanego układu sterowania sformułować można zatem w postaci wymagania, aby wyznacznik
macierzy występującej we wzorze (5) nie równał się tożsamościowo zeru. Jeżeli warunek ten jest spełniony, odpowiednie operatorowe macierze istnieją i można je wyznaczyć na podstawie wzoru

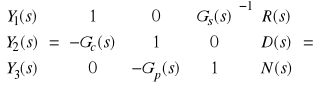
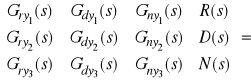
(6)

.

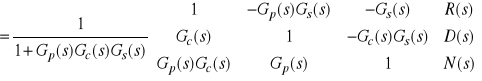
Gdy transmitancje
,
oraz
są właściwymi funkcjami wymiernymi zmiennej zespolonej
, warunek dobrej określoności układu sterowania rozszerza się o wymaganie, aby wszystkie elementy macierzy odwrotnej występującej we wzorze (6) były także właściwymi funkcjami wymiernymi zmiennej
. Jak łatwo pokazać, konieczny i wystarczający warunek tak zdefiniowanej dobrej określoności układu sterowania przyjmuje postać żadania, aby wyznacznik
nie miał postaci ściśle właściwej wymiernej funkcji zmiennej zespolonej
, co zapisujemy jako
. Rozważany układ sterowania jest wewnętrznie stabilny, gdy żadna z dziewięciu transmitancji, stanowiących elementy odwrotnej macierzy ze wzoru (6), nie posiada biegunów w prawej domkniętej półpłaszczyźnie płaszczyzny zespolonej. Konieczny i wystarczający warunek wewnętrznej stabilności tego układu sformułować można w postaci podwójnego wymagania:

- wyznacznik
nie posiada zer w prawej domkniętej półpłaszczyźnie płaszczyzny zespolonej,

- w iloczynie
nie występują skreślenia w parach złożonych z zera i bieguna z prawej domkniętej półpłaszczyzny płaszczyzny zespolonej.

W przypadku operatorowych transmitancji (1) mamy

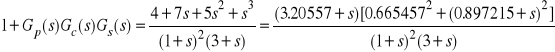
. (7)

Na tej podstawie stwierdzamy, iż rozważany układ sterowania, będąc układem dobrze określonym, nie spełnia jednak warunku wewnętrznej stabilności: w iloczynie
występuje bowiem niedozwolone skreślenie w parze złożonej z bieguna
transmitancji sterowanego obiektu oraz zera
transmitancji sterownika. Operatorowe transmitancje w odpowiednich relacjach mają postać:

,
,
,

,
,
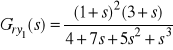
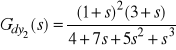
, (8)

,
,
.

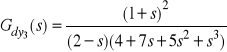
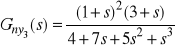
Wyniki te potwierdzają tezę o wewnętrznej niestabilności badanego układu: transmitancje
oraz
posiadają dodatni biegun
. Układ ten rozpatrywany ze względu na wpływ zadającego sygnału
oraz pomiarowego szumu
na sterowaną wielkość
jest układem stabilnym w sensie BIBO, co łatwo sprawdzić. Mamy

, (9)

. (10)

Przykład 5 (Stabilność i dokładność)

Jest dany układ zamknięty jak na rys. A.

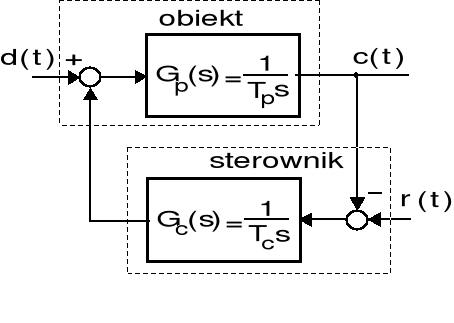
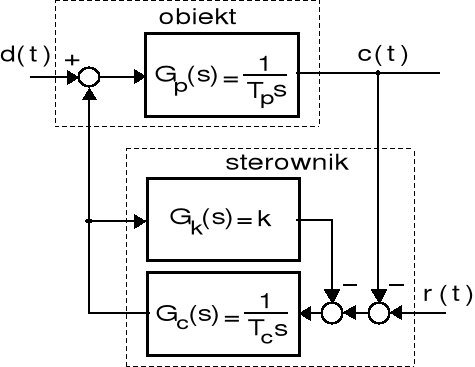
Rys. A. Strukturalny schemat układu sterowania Rys. B. Strukturalny schemat skorygowanego

układu sterowania

a) Pokaż, że układ ten nie może osiągnąć jakiegokolwiek celu sterowania, z uwagi na swą strukturalną niestabilność.

b) Jaki jest najprostszy środek stabilizującej korekcji tego układu, jeżeli dopuszcza się niezerowy uchyb ustalony, będący reakcją na skokowe zakłócenie
?

c) Zakładając, że jednostkowe zakłócenie skokowe
nie powinno powodować ustalonego uchybu większego niż 0.01, wyznacz parametry owego korektora.

d) Jaka jest dokładność odtwarzania skokowo zmieniającego się sygnału zadanego
, dla układu wyznaczonego w punktach b i c?

Rozwiązanie

a) Z transmitancji układu zamkniętego,
, wynika, że niezależnie od wartości parametrów
oraz
nie można spełnić koniecznego i wystarczającego warunku stabilności tego układu - układ jest więc strukturalnie niestabilny.

b) Układ z rysunku A można ustabilizować tylko wtedy, gdy zmieni się jego strukturę. Ponieważ dopuszcza się występowanie niezerowych ustalonych uchybów, będących reakcją na skokowe zakłócenia na wejściu obiektu, najprostszym środkiem takiej korekcji jest zastosowanie sztywnego sprzężenia zwrotnego przekształcającego sterownik typu I w sterownik typu P z inercją. Tak skorygowany układ przedstawia się jak na rys. B.

c) Wyznaczywszy zakłóceniową transmitancję
układu z rys. B, stwierdzamy, że układ ten jest stabilny dla dowolnych
i
, większych od zera. Z wymagania, by ustalony uchyb sterowania wywołany zakłóceniem skokowym
nie przekraczał 0.01, otrzymujemy zatem warunek
.

d) Zamknięty układ sterowania, uzyskany w punktach b i c, jest układem astatycznym pierwszego rzędu w odniesieniu do sygnału zadającego, co oznacza, iż ustalony uchyb odtwarzania skokowo zmieniającego się sygnału zadającego jest zerowy.

Przykład 6 (Stabilność i dokładność)

Strukturalny schemat, będący modelem pewnego zamkniętego układu sterowania, przedstawia się jak na poniższym rysunku, gdzie
,
oraz
oznaczają transmitancje, odpowiednio: sterowanego obiektu, sterownika PI oraz kanału zakłóceniowego. Przyjmując dodatnie wartości parametrów sterownika
oraz
, zbadaj ustaloną wartość uchybu sterowania w tym układzie, przy założeniu sygnału zadającego oraz zakłócenia w postaci jednostkowych skoków położeniowego i prędkościowego.

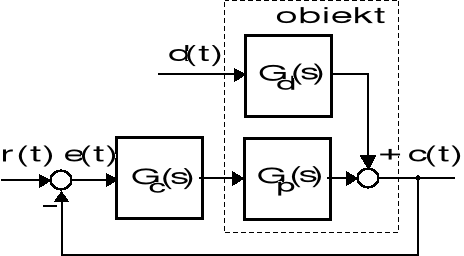
Strukturalny schemat układu sterowania

Rozwiązanie

Uchyb sterowania wyznaczamy ze wzoru
, gdzie
jest uchybem sterowania w układzie, nie podlegającym oddziaływaniu zakłóceń (uchyb sygnałowy), zaś
jest reakcją zamkniętego układu na zakłócenia (uchyb zakłóceniowy). Zacznijmy od wyznaczenia składnika
uchybu
. Zakładając, iż rozpatrywany zamknięty układ sterowania jest stabilny (co, jak łatwo sprawdzić, zachodzi dla dowolnych założonych dodatnich wartości
oraz
), mamy
, gdzie

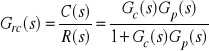
. (1)

Składnik
uchybu dany jest wzorem

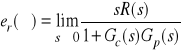
. (2)

W rozważanym przypadku mamy
. Ze względu na sygnał zadający, układ sterowania charakteryzuje się astatyzmem pierwszego rzędu. Ustalony uchyb pochodzący od skokowego sygnału zadającego (
) równa się zero, natomiast w przypadku prędkościowego sygnału zadającego (
) otrzymamy
, gdzie
jest wzmocnieniem prędkościowym. Dla zakłóceniowego składnika uchybu zachodzi
, gdzie
oznacza zakłóceniową transmitancję układu zamkniętego. Jak łatwo sprawdzić, obowiązują następujące zależności

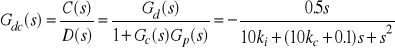
, (3)

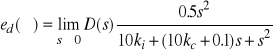
. (4)

Ze względu na zakłóceniowe wejście, badany układ sterowania przedstawia się jako astatyczny pierwszego rzędu. Tak więc obserwujemy zerowy uchyb ustalony dla zakłócenia skokowego oraz niezerowy uchyb odtwarzania sygnału prędkościowego, wynoszący
.

Przykład 7 (Synteza sterownika w oparciu o transmitancję wzorcową)

Dany jest strukturalny schemat dwupętlowego układu sterowania, będącego serwomotorem prądu stałego z proporcjonalnym sterownikiem oraz prędkościowym korekcyjnym sprzężeniem zwrotnym. Znajdź wartości parametrów
oraz
, zapewniające odpowiedzi skokowej układu zamkniętego przeregulowanie
oraz czas wystąpienia przeregulowania (czas maksimum)
. Jaka jest wartość czasów ustalania
oraz
odpowiedzi skokowej tak nastawionego układu sterowania?

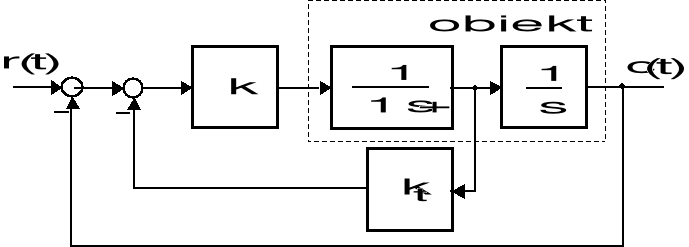
Strukturalny schemat dwupętlowego układu sterowania

Rozwiązanie

Operatorową transmitancję rozważanego układu zamkniętego, daną wzorem

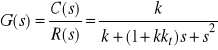
, (1)

przedstawić można w standardowej postaci

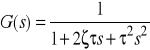
, gdzie
oraz
. (2)

Przeregulowanie
oraz czas maksimum
odpowiedzi skokowej układu modelowanego tą transmitancją dane są znanymi formułami

,
przy
, (3)

z których wynika, iż
oraz
. Dla numerycznych danych przykładu uzyskuje się
oraz
, a następnie
oraz
. Oszacowania czasów ustalania odpowiedzi skokowej mają postać:
oraz
. "Dokładne" wartości czasów ustalania (obliczone symulacyjnie) wynoszą:
oraz
.

Przykład 8 (Synteza sterownika w oparciu o transmitancję wzorcową)

Dany jest strukturalny schemat układu sterowania jak na poniższym rysunku. W układzie tym występuje szeregowy sterownik o wzmocnieniu k oraz dwie pętle ujemnego sprzężenia zwrotnego: zewnętrzna pętla jednostkowego sprzężenia położeniowego oraz wewnętrzna pętla sprzężenia prędkościowego - wzmocnienie sygnału w torze prędkościowego sprzężenia wynosi
.

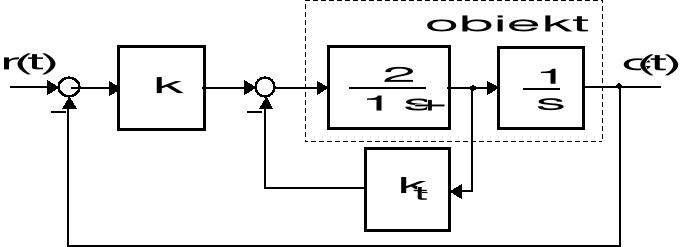
Strukturalny schemat układu sterowania serwomotorem prądu stałego

Należy dobrać takie wartości parametrów k oraz
, aby zamknięty układ był tłumiony krytycznie, zaś czas ustalania odpowiedzi skokowej tego układu wynosił
.

Rozwiązanie

Operatorowa transmitancja rozważanego zamkniętego układu sterowania dana jest wzorem

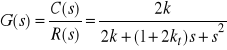
. (1)

Tę transmitancję drugiego rzędu przedstawić możemy w następującej standardowej postaci

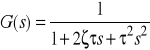
, (2)

gdzie
oraz
. Z wymagań postawionych zamkniętemu układowi sterowania wynika, że
. Transmitancja (2) przyjmuje zatem postać
. Odpowiedź skokowa rozważanego układu dana jest przeto wzorem

. (3)

Niech
oznacza czas ustalania tej odpowiedzi dla kontrolnej strefy o założonej szerokości
. Zachodzi zatem
. Rozwiązania tego nieliniowego równania dla
oraz
mają postać odpowiednio:
oraz
. Warto zwrócić uwagę, iż przy
powyższe wartości czasów ustalania
znacznie różnią się od odpowiednich przybliżonych wartości, uzyskanych w oparciu o często zalecane uproszczone formuły
oraz
. Formuły te są bowiem słuszne tylko w przypadku słabo tłumionych (
) odpowiedzi skokowych. Ze wzoru
wynika, iż
, czemu odpowiada
oraz
. Zastosowanie wzoru
prowadzi do parametrów k oraz
o wartościach znacznie różniących się od tych, które wyznaczono wyżej:
oraz
. W efekcie tak nieprawidłowo zaprojektowany układ sterowania charakteryzowałby się odpowiedzią skokową wolniejszą od wymaganej.

Przykład 9 (Synteza sterownika w oparciu o transmitancję wzorcową)

Na rysunku danym niżej przedstawiono schemat układu sterowania położeniem z wykorzystaniem sygnału pomiarowego proporcjonalnego do prędkości elementu wykonawczego. Na sterowany obiekt, obok sygnału sterującego, oddziałują także zakłócenia
.

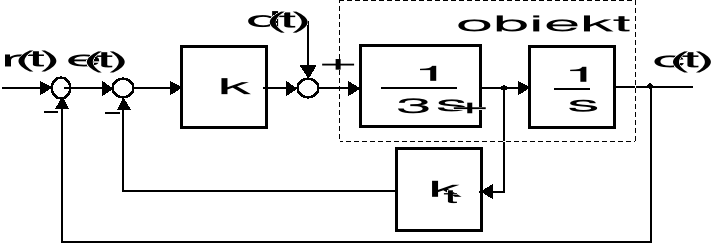
Strukturalny schemat układu sterowania

Dobierz takie wartości nastawialnych parametrów k oraz
rozważanego układu, aby dla krytycznego zakłócenia
w postaci skoku jednostkowego wartość bezwzględna uchybu sterowania w stanie ustalonym nie przekraczała
, zaś czas ustalania sygnałowej odpowiedzi skokowej zamkniętego układu wynosił
. Oszacuj przeregulowanie
tej odpowiedzi.

Rozwiązanie

Sygnałowa transmitancja operatorowa układu zamkniętego dana jest wzorem

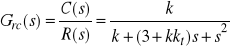
, (1)

zaś zakłóceniową uchybową transmitancję operatorową tego układu określa wzór

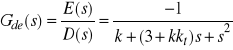
. (2)

Przy założonej postaci zakłócenia (
), bezwzględna wartość ustalonego uchybu wynosi
,
. Na tej podstawie uzyskujemy ograniczenie
. Przedstawiając transmitancję (1) w standardowej postaci

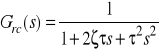
, (3)

otrzymujemy wzory:
oraz
. Z kolei, szacując czas ustalania
jako
, na podstawie warunków zadania dostajemy
. Przyjmijmy minimalną ze względu na wymagane tłumienie wpływu zakłóceń wartość wzmocnienia
. Ze wzoru
otrzymujemy przeto, iż
. Takiej wartości współczynnika tłumienia odpowiada przeregulowanie

. (4)

Parametr
, wynikający ze wzoru
, równa się
, zachodzi przy tym
. Sygnałowa odpowiedź skokowa tak zaprojektowanego układu sterowania charakteryzuje się czasem ustalania
, spełniającym postawione wymaganie.

Przykład 10 (Synteza sterownika w oparciu o transmitancję wzorcową)

Na poniższym rysunku dany jest schemat układu sterowania, przy czym
oraz
. Należy w ten sposób dobrać wartość wzmocnienia k oraz stałej różniczkowania
, aby amplitudowa charakterystyka transmitancji układu zamkniętego opisana była parametrami: wskaźnikiem oscylacyjności
oraz pasmem przenoszenia
. Ponadto należy oszacować przeregulowanie
, czas maksimum
oraz czas ustalania
odpowiedzi skokowej tego układu.

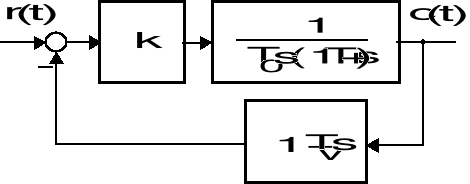
Strukturalny schemat układu sterowania

Rozwiązanie

Operatorowa transmitancja rozważanego zamkniętego układu sterowania dana jest wzorem

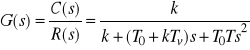
. (1)

Transmitancję tę przedstawiamy w standardowej postaci

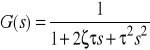
, gdzie
oraz
. (2)

Na podstawie podanych wzorów zapisać można zależność

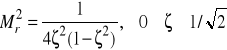
, (3)

z której wynika formuła

, (4)

łącząca wskaźnik oscylacyjności
ze współczynnikiem tłumienia
. Parametr
transmitancji (2) związany jest z pasmem przenoszenia
układu modelowanego tą transmitancją oraz ze współczynnikiem tłumienia
następującym wzorem

. (5)

Biorąc pod uwagę warunki zadania, otrzymujemy
oraz
. Wartości nastawialnych parametrów układu sterowania wynoszą zatem:
oraz
. Skokowa odpowiedź tego układu opisana jest następującymi wskaźnikami:
,
,
oraz
.

Zadania do samodzielnego rozwiązania

Zadanie 1

Dane jest równanie:
. Korzystając z kryterium Routha-Hurwitza, określ liczbę pierwiastków tego równania o części rzeczywistej większej od
. Wskazówka: należy dokonać postawienia
, a następnie zastosować kryterium Routha-Hurwitza w stosunku do tak otrzymanego wielomianu zespolonej zmiennej
.

Odpowiedź

Równanie to ma trzy pierwiastki o części rzeczywistej większej niż
.

Zadanie 2

Dane jest równanie charakterystyczne pewnego układu dynamicznego:

a)
,

b)
,

c)
,

d)
,

e)
.

Konstruując odpowiednią tablicę Routha, określ liczbę pierwiastków tego równania, leżących w prawej domkniętej półpłaszczyźnie płaszczyzny zespolonej.

Odpowiedź

a) Rozważane równanie ma dwa pierwiastki leżące w prawej półpłaszczyźnie płaszczyzny zespolonej.

b) Równanie to ma jeden pierwiastek leżący w prawej półpłaszczyźnie płaszczyzny zespolonej oraz dwie pary pierwiastków sprzężonych zespolonych o zerowych częściach rzeczywistych.

c) Rozważany układ dynamiczny jest układem niestabilnym: dwa pierwiastki równania charakterystycznego leżą w prawej półpłaszczyźnie.

d) Rozważany układ dynamiczny jest układem niestabilnym: jego równanie charakterystyczne ma jeden pierwiastek leżący w prawej półpłaszczyźnie oraz parę urojonych pierwiastków sprzężonych zespolonych.

e) Współczynniki równania przy dwóch najniższych potęgach zespolonej zmiennej
mają wartość zero. Oznacza to, iż równanie to posiada podwójny pierwiastek w zerze. Kryterium Routha-Hurwitza należy zatem stosować do zredukowanego równania charakterystycznego o postaci
. Tak postępując, stwierdzono, iż badane równanie posiada dwa pierwiastki urojone.

Zadanie 3

Układ sterowania z jednostkowym ujemnym sprzężeniem zwrotnym składa się ze sterowanego obiektu o operatorowej transmitancji
,
,
oraz sterownika PI opisanego operatorową transmitancją
. Posługując się kryterium Routha, wyznacz taki obszar na płaszczyźnie nastaw
sterownika, któremu odpowiada BIBO stabilny zamknięty układ sterowania.

Odpowiedź

Warunki stabilności zamkniętego układu w sensie BIBO określone są następująco

oraz
.

Zadanie 4

W układzie sterowania z obiektem o transmitancji
, gdzie
oraz
, zastosowano jednostkowe ujemne sprzężenie zwrotne oraz sterownik PI o transmitancji
. Posługując się kryterium Routha, określ warunki jakie muszą spełniać nastawy
oraz
tego sterownika, aby zamknięty układ sterowania był układem stabilnym w sensie BIBO.

Odpowiedź

Warunki BIBO stabilności zamkniętego układu sterowania dane są wzorami

oraz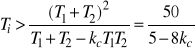
.

Zadanie 5

Strukturalny schemat układu sterowania ma postać jak na poniższym rysunku.

Strukturalny schemat układu sterowania

Stosując algebraiczne kryterium stabilności, wyznacz krytyczną wartość
wzmocnienia układu otwartego
,
, przy której zamknięty układ osiąga granicę stabilności. W przypadku jakich stałych czasowych
i
owa wartość osiąga minimum?

Odpowiedź

Krytyczne wzmocnienie układu otwartego wynosi:

. Tak więc wzmocnienie to nie zależy od bezwzględnych wartości stałych czasowych
oraz
, ale od stosunku tych stałych. Na podstawie powyższego wzoru łatwo stwierdzić, że
osiąga minimum
przy
.

Zadanie 6

Dynamiczny obiekt o operatorowej transmitancji
,
, jest sterowany w zamkniętym układzie z jednostkowym ujemnym sprzężeniem zwrotnym za pomocą sterownika PD o transmitancji
. Posługując się algebraicznym kryterium stabilności, określ jak należy dobierać wartość stałej czasowej
tego sterownika, by zamknięty układ był stabilny w sensie BIBO dla dowolnej dodatniej wartości parametru
.

Odpowiedź

Układ zamknięty jest stabilny przy
.

Zadanie 7

Układ sterowania ma strukturę jak na rysunku danym niżej, przy czym wartości parametrów
,
,
oraz
są dodatnie.

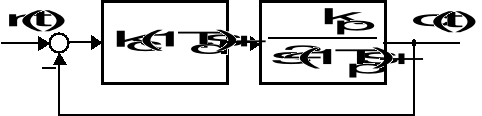
Strukturalny schemat układu sterowania

Powiększanie wartości parametru
sterownika prowadzi do wzrostu przyspieszeniowego wzmocnienia tego układu. Jaka jest graniczna z uwagi na stabilność wartość tego parametru, przy założeniu, że powyższy liniowy model obowiązuje bez ograniczeń?

Odpowiedź

Warunek stabilności ma postać
, Stabilność rozważanego układu nie zależy od wartości iloczynu
.

Zadanie 8

Czy układ sterowania o strukturalnym schemacie danym na rysunku jest układem dobrze określonym oraz wewnętrznie stabilnym?

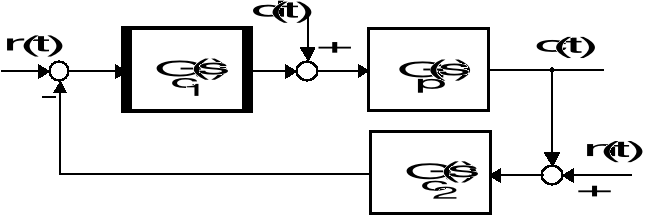
Strukturalny schemat układu sterowania

Rozważ następujące przypadki transmitancji sterowanego obiektu
, sterownika w głównym torze sterowania
oraz sterownika w torze sprzężenia zwrotnego
:

a)
,
,
,

b)
,
,
,

c)
,
,
,

d)
,
,
,

e)
,
,
.

Odpowiedź

a,c,e) Układ jest dobrze określony oraz wewnętrznie niestabilny.

b,d) Układ, będąc wewnętrznie stabilnym, nie jest układem dobrze określonym.

Zadanie 9

Sprawdź, czy układ sterowania o strukturalnym schemacie przedstawionym na poniższym rysunku jest układem wewnętrznie stabilnym. Transmitancje
oraz
mają postać

,
.

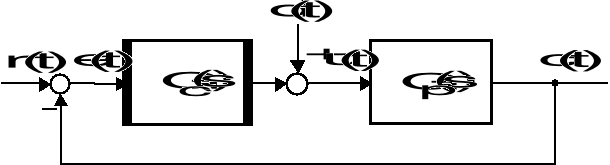
Strukturalny schemat układu sterowania

Odpowiedź

Rozważany układ sterowania jest wewnętrznie niestabilny.

Zadanie 10

Układ sterowania składa się z obiektu o transmitancji
oraz proporcjonalnego sterownika o wzmocnieniu k, objętych jednostkowym ujemnym sprzężeniem zwrotnym. Sprawdź, czy dobierając wzmocnienie k można zapewnić ustalony uchyb
przy jednostkowym skokowym sygnale zadającym. Jeżeli nie jest to możliwe, określ minimalną wartość tego uchybu, możliwą do uzyskania w układzie sterowania.

Odpowiedź

Minimalna ze względu na stabilność zamkniętego układu sterowania wartość uchybu ustalonego wynosi
. Oszacowanie to ma jednak walor tylko teoretyczny. Niezbędne jest bowiem uwzględnienie odpowiedniego zapasu stabilności układu sterowania. Przykładowo, przyjmując zapas wzmocnienia
, uzyskuje się "praktyczną" ocenę ustalonego uchybu, możliwego do uzyskania w tym układzie:
.

Zadanie 11

Dynamiczny obiekt opisany operatorową transmitancją
sterowany jest w układzie zamkniętym z jednostkowym ujemnym sprzężeniem zwrotnym przy pomocy sterownika całkującego
.

a) Oblicz wartość stałej całkowania
tego sterownika, dla której skokowa odpowiedź układu sterowania charakteryzuje się przeregulowaniem
. Dla tak zaprojektowanego układu oszacuj ustaloną wartość uchybu śledzenia jednostkowego prędkościowego sygnału zadającego.

b) Zakładając, iż uchyb ten nie powinien przekraczać 0.1, wyznacz odpowiednią wartość stałej całkowania
sterownika
, a następnie oszacuj wartość przeregulowania
skokowej odpowiedzi otrzymanego w ten sposób układu zamkniętego.

Odpowiedź

a) Wartość stałej całkowania, zapewniającej zamkniętemu układowi skokową odpowiedź o przeregulowaniu
, wynika ze wzoru
, gdzie
. Dla
otrzymuje się
, czemu odpowiada wartość
, ustalony prędkościowy uchyb
.

b) Dla
otrzymuje się stałą całkowania
oraz skokową odpowiedź o przeregulowaniu
.

Zadanie 12

Strukturalny schemat pokazany na poniższym rysunku jest modelem serwomechanizmu. Na układ ten działa zadający sygnał w postaci prędkościowego skoku
oraz zakłócenie w postaci skoku położeniowego
(moment obciążenia).

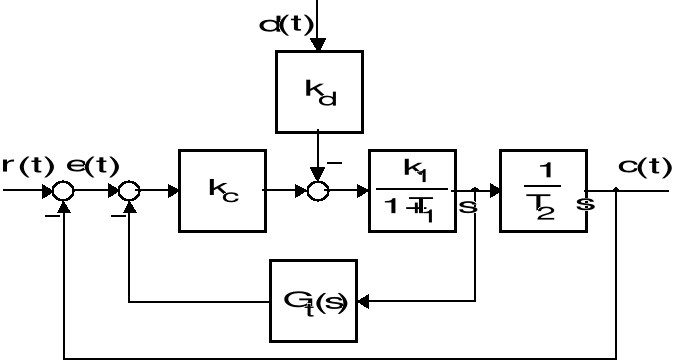
Schemat serwomechanizmu

a) Wyznacz ustalony uchyb
w zależności od prędkości
narastania sygnału zadającego i intensywności d zakłócenia, w przypadku, gdy
.

b) Wyznacz ustalony uchyb prędkościowy
, w przypadku, w którym zastosowano proporcjonalne ("sztywne") sprzężenie zwrotne
,
, oraz w przypadku, gdy korekcyjne sprzężenie zwrotne ma charakter dynamiczny:
. Jaką wartość przyjmuje ustalony uchyb położeniowy
pochodzący od zakłócenia
?

Odpowiedź

a) Wartość ustalonego uchybu wynosi
.

b) W przypadku proporcjonalnego sprzężenia korekcyjnego, ustalony uchyb prędkościowy wynosi
. W przypadku dynamicznego korekcyjnego sprzężenia zwrotnego ustalony uchyb prędkościowy równa się
.

Zadanie 13

Na rysunku pokazano strukturalny schemat układu sterowania złożonego z serwomotoru prądu stałego oraz wzmacniacza mocy (sterownika proporcjonalnego).

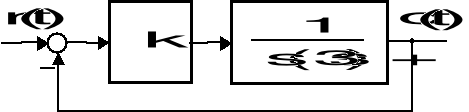
Strukturalny schemat układu sterowania

Określ wartość wzmocnienia k, przy której układ zamknięty jest: a - układem o oscylacyjnym charakterze, b - układem o krytycznym tłumieniu oraz c - układem przetłumionym.

Odpowiedź

Układ jest układem oscylacyjnym dla
, krytycznie tłumionym dla
oraz przetłumionym dla
.

Zadanie 14

Obiekt dynamiczny, którego model dany jest następującą operatorową transmitancją

,

jest sterowany w układzie zamkniętym z jednostkowym ujemnym sprzężeniem zwrotnym za pośrednictwem proporcjonalnego sterownika o wzmocnieniu k.

a) Przy jakich k odpowiedź skokowa tego układu będzie miała oscylacyjny charakter?

b) Wyznacz wartość k, przy której przeregulowanie
odpowiedzi skokowej układu zamkniętego wyniesie
.

c) Oblicz ustaloną wartość tej odpowiedzi dla k wyznaczonego w punkcie b.

Odpowiedź

a) Odpowiedź układu zamkniętego będzie miała oscylacyjny charakter przy
.

b) Przeregulowanie odpowiedzi skokowej ma wartość
dla
.

c) Ustalona wartość odpowiedzi skokowej układu wynosi
.

Zadanie 15

Dany jest strukturalny schemat układu sterowania jak na rysunku

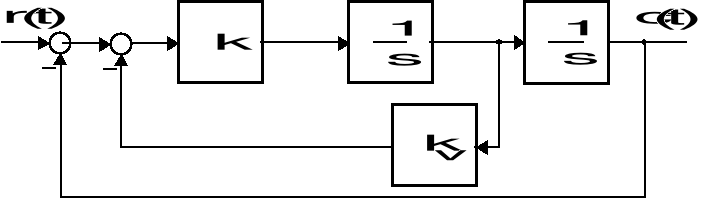
Strukturalny schemat układu sterowania

a) Podaj operatorową transmitancję układu zamkniętego.

b) Zakładając, iż
, wyznacz wartość ustaloną odpowiedzi tego układu.

c) Odpowiedź zamkniętego układu na skokowy sygnał
osiąga bez przeregulowań wartość ustaloną w najkrótszym czasie, jeżeli współczynnik tłumienia transmitancji tego układu równa się
. Wyznacz parametr
, przy którym ten warunek zachodzi.

d) Zakładając, iż układ o parametrach określonych w punkcie c ma osiągnąć (z dokładnością
) stan ustalony po 6 sekundach od momentu przyłożenia skokowego sygnału zadającego, znajdź wartość parametru k, która zapewnia spełnienie tego wymagania.

Odpowiedź

a) Transmitancja rozważanego układu zamkniętego ma postać
.

b) Wartość ustalona odpowiedzi wynosi
.

c) Poszukiwany warunek dany jest wzorem
,
.

d) Wymagania spełniają parametry
oraz
.

Zadanie 16

Na rysunku dany jest strukturalny schemat pewnego układu sterowania. Należy tak dobrać wartości współczynników
,
oraz
, aby układ ten charakteryzował się jednostkowym statycznym wzmocnieniem oraz skokową odpowiedzią o przeregulowaniu
i czasie ustalania
.

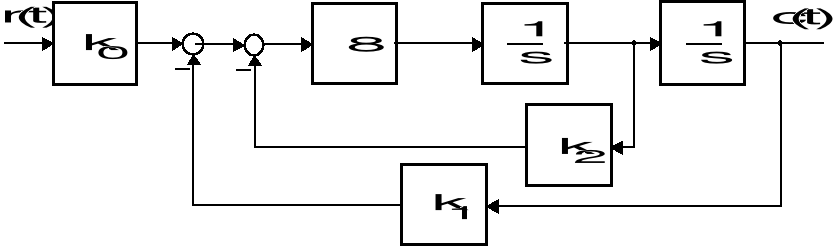
Strukturalny schemat układu sterowania

Odpowiedź

Układ o parametrach
oraz
posiada odpowiedź skokową opisaną wskaźnikami:
oraz
.

Zadanie 17

Dany jest następujący strukturalny schemat układu sterowania.

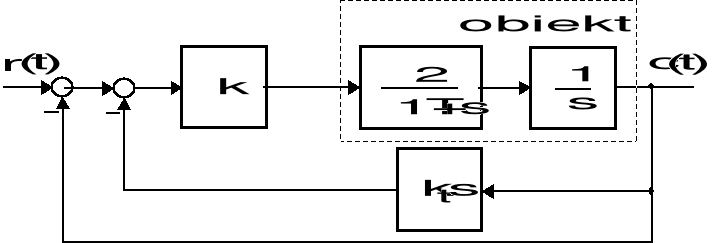
Strukturalny schemat układu sterowania

W wyniku identyfikacyjnego eksperymentu ustalono, iż odpowiedź skokowa układu, w którym nie występuje sprzężenie prędkościowe (
), charakteryzuje się przeregulowaniem
oraz czasem ustalania
. Uznano, iż proces przejściowy o takich wskaźnikach nie spełnia stawianych wymagań - żąda się bowiem dwukrotnie mniejszego przeregulowania, a także dwukrotnie mniejszego czasu ustalania. Wyznacz takie wartości parametrów k oraz
, które zapewnią wymaganą jakość procesu przejściowego.

Odpowiedź

Z eksperymentu identyfikacyjnego wynika następujące oszacowanie stałej czasowej
obiektu:
. Traktując
jako nominalny parametr transmitancji obiektu, wyznaczono wartości nastawialnych parametrów układu sterowania:
oraz
. "Rzeczywista" wartość stałej czasowej obiektu wynosi
. Symulując odpowiedź skokową tak zaprojektowanego układu, stwierdzono, iż
oraz
.

Zadanie 18

Strukturalny schemat układu sterowania, złożonego z inercyjnego obiektu, objętego korekcyjnym sprzężeniem zwrotnym oraz całkującego sterownika, przedstawiono na rysunku.

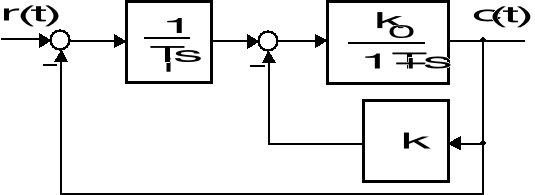
Strukturalny schemat układu sterowania

Parametry operatorowej transmitancji obiektu wynoszą:
oraz
. Należy tak dobrać wartość parametru
sterownika oraz wartość wzmocnienia k toru korekcyjnego sprzężenia zwrotnego, aby przeregulowanie odpowiedzi skokowej układu zamkniętego wynosiło
, zaś pasmo przenoszenia tego układu miało wartość
.

Odpowiedź

Nastawialne parametry układu sterowania wynoszą:
oraz
.

Zadanie 19

Układ dynamiczny drugiego rzędu opisany jest transmitancją
. Przy jakiej wartości
pasmo przenoszenia tego układu będzie równe pulsacji drgań nietłumionych?

Odpowiedź

Poszukiwana wartość współczynnika tłumienia wynosi
.

Zadanie 20

Na rysunku dany jest schemat pewnego układu sterowania, przy czym
oraz
.

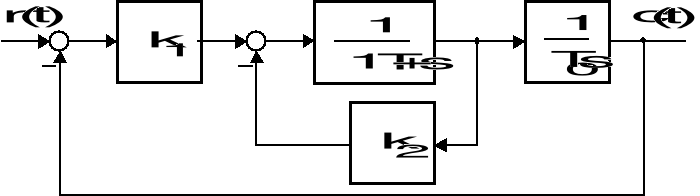
Strukturalny schemat układu sterowania

Wyznacz
oraz
, zapewniające amplitudowej charakterystyce transmitancji tego układu wskaźnik oscylacyjności
oraz pasmo przenoszenia
. Oszacuj wskaźniki
,
oraz
odpowiedzi skokowej tak zaprojektowanego układu.

Odpowiedź

Parametry
oraz
prowadzą do układu o odpowiedzi skokowej opisanej wskaźnikami:
,
,
oraz
.

27

---