Rozkłady zmiennych losowych ciągłych:
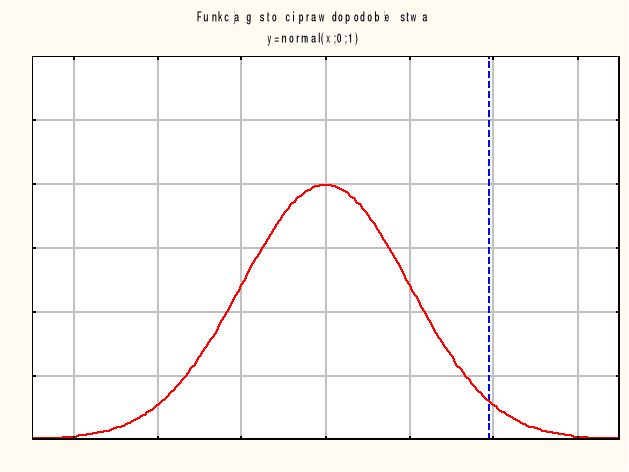
Rozkład normalny:
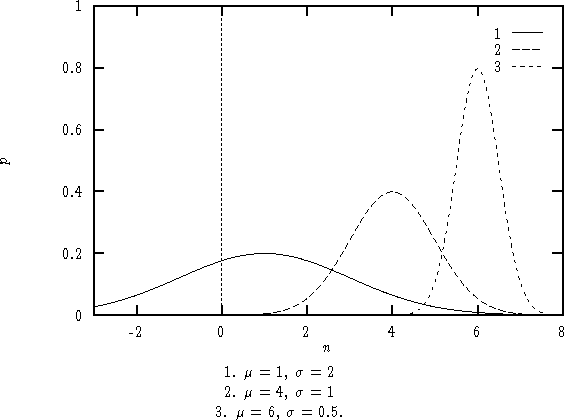
Rozkład zależy od dwóch parametrów: μ i σ, które są jednocześnie wartością oczekiwaną i
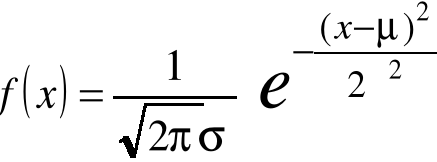
odchyleniem standardowym (pierwiastkiem z wariancji) tego rozkładu. Funkcja gęstości tego rozkładu:
Liczba e jest stałą matematyczną i w przybliżeniu wynosi 2,72.
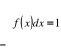
Reguła trzech sigm
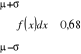
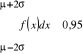
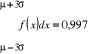
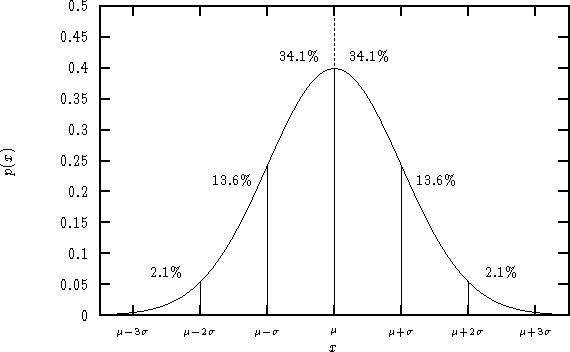
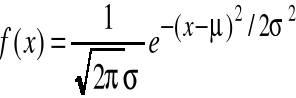
Standaryzacja zmiennej losowej:
Jeśli
X ~ . (μ, σ)
to zmienna (X- μ)/σ ~ .. (0,1).
W przypadku zmiennej losowej normalnej zestandaryzowana zmienna też ma rozkład normalny i jest oznaczana zwykle literą U lub z. My będziemy oznaczać literą U.
Rozkład U jest stablicowany. Z tablic można odczytać prawdopodobieństwa dla różnych przedziałów oraz wartości graniczne dla zadanych z góry prawdopodobieństw.
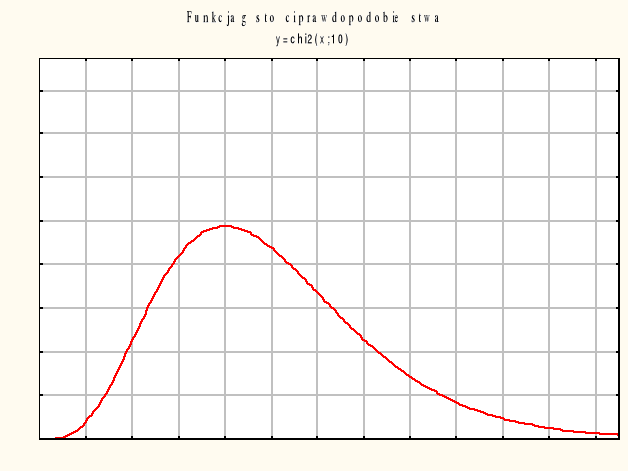
Rozkład chi-kwadrat (χ2).
Niech U1, U2, ..., Uk będą niezależnymi standaryzowanymi normalnymi zmiennymi losowymi. Wówczas zmienną losową
χ2(k) = (U1)2+(U2)2 + ... +(Uk)2
nazywać będziemy zmienną o rozkładzie chi-kwadrat. Zmienna ta przyjmuje tylko wartości dodatnie i ma rozkład niesymetryczny uzależniony tylko od jednego parametru k, zwanego stopniami swobody:
E[χ2(k)]=k, Var[χ2(k)]=2k.
Gęstość prawdopodobieństwa rozkładu chi-kwadrat
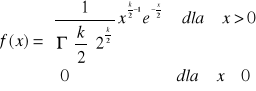
gdzie Γ jest funkcją gamma Eulera,
Γ(z) =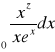
, Γ(![]()
) = ![]()
, Γ(k)=(k-1)!.
Rozkład t-Studenta
Niech zmienne U i zmienna χ2(k) będą zmiennymi niezależnymi. Wówczas zmienną losową
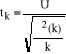
nazywać będziemy zmienną losową o rozkładzie t-Studenta (z k- stopniami swobody).
Jest to rozkład symetryczny: E(tk)=0, Var(tk)= k/(k-2).
Gęstość prawdopodobieństwa rozkładu Studenta
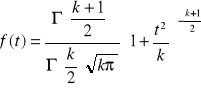
Rozkład Studenta zbliża się do rozkładu normalnego N(0, 1), staje się coraz mniej spłaszczony dla rosnących k i dla k=∞ pokrywa się z nim.
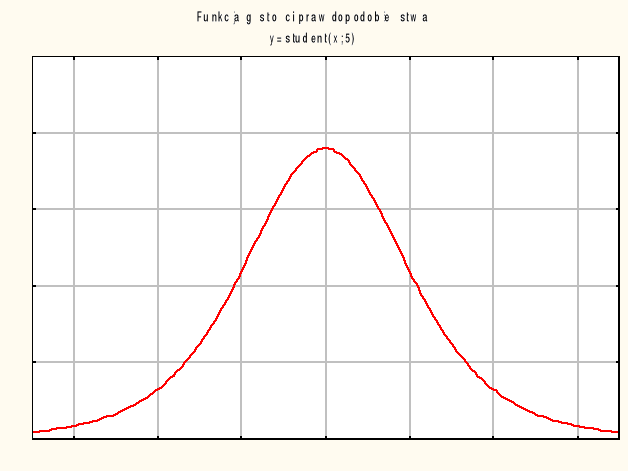
Rozkład F Snedecora
Niech zmienne χ2(k1) i zmienna χ2(k2) będą zmiennymi niezależnymi. Wówczas zmienną losową
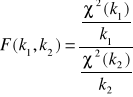
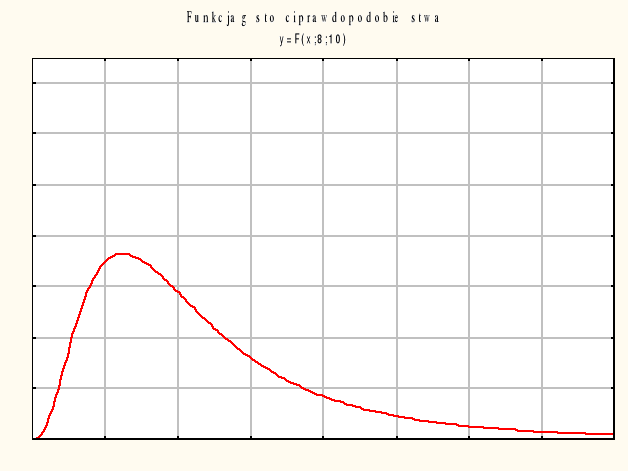
nazywać będziemy zmienną o rozkładzie F Snedecora z parą stopni swobody (k1,k2). Zmienna ta przyjmuje tylko wartości dodatnie i ma rozkłada niesymetryczny:
E[F(k1,k2)]=k2/(k2-2) , Var[F(k1,k2)]= 2(k2)2(k1 +k2+2)/[k1(k2-2)2 (k2-4)
Gęstość prawdopodobieństwa tego rozkładu:
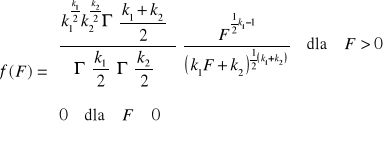
![]()
![]()
Wyszukiwarka