FUNKCJE, WYKRESY, WŁASNOŚCI (zakres podstawowy)
1. Znajdź wzór funkcji liniowej: a) której wykres przechodzi przez punkty A=(-2;4) i B=(6;1)
b) której wykres jest nachylony do osi x pod kątem 60o i przechodzi przez punkt (0;![]()
)
2. Dana jest funkcja liniowa y = 3x - 7 podaj po trzy przykłady funkcji liniowych, których wykresy są
odpowiednio a) równoległe b) prostopadłe do wykresu danej funkcji .
3. Znajdź wzór funkcji liniowej , której wykres jest a) równoległy b) prostopadły do wykresu funkcji
y = -5x + 3 i przechodzi przez punkt A(10;2)
4 Dane są funkcje: a) ![]()
b) ![]()
c) ![]()
![]()
d) ![]()
.
Pod jakim kątem ich wykresy przecinają oś x ?
5.Oblicz miejsca zerowe funkcji: a)![]()
, b) ![]()
x2 +x -2, c) f(x)= x3 - 4x2- 2x +8 d) ![]()
![]()
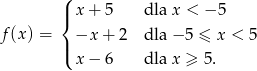
e) ![]()
f) g) h) ![]()
6.Wyznacz współrzędne punktów przecięcia się wykresu funkcji z osiami układu współrzędnych:
![]()
a) y = 4x + 7 b) y = x2- 9 c) f(x) = x3 + 4x2 - 5x d) e) ![]()
7. Narysuj wykresy funkcji: a) y = x + 3 dla ![]()
b) f(x)= x2+6x +5 c) ![]()
d) ![]()
![]()
e) ![]()
f) ![]()
g) f(x) = - x +2 dla ![]()
h)
8. Ustal dziedzinę funkcji : a) f(x)= 5x3+2x-4 b) ![]()
c) ![]()
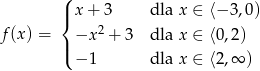
d) ![]()
e) ![]()
f) g) ![]()
9. Dla jakich wartości parametru m a) do wykresu funkcji y= (m+6)x - 3m+2 należy punkt (-2;4m) ?
b) miejscem zerowym funkcji y = (4m - 5)x+2 jest liczba 5 ? c) wykresy funkcji ![]()
i funkcji
y=(4m -2 )x są do siebie równoległe? d) wykresy funkcji f(x)= -mx+3 i funkcji f(x)=(2m + 1)x+5m są do siebie
prostopadłe? e) funkcja y=(7m+14)x +5m +6 jest rosnąca, malejąca lub stała? f) funkcja y = ( m2+3m- 4)x +12
jest rosnąca, malejąca lub stała? g) funkcja f(x)=(5-2m)x2+4x - 3 przybiera wartość największą a dla jakiego m
najmniejszą? h) pierwiastkiem wielomianu W(x) = - mx3+ 4mx2 - x +3m jest liczba -3 ? i) do wykresu funkcji
![]()
należy punkt A=(m;![]()
) ? j) wierzchołkiem paraboli y = x2 + 4mx - 6 jest punkt o odciętej x = 6 ?
k) osią symetrii paraboli y = 2x2 + 8mx +3 jest prosta x = -4 ? l) funkcja y=(2m-7)x+5 nie ma miejsca zerowego?
10.Oblicz wskazane obok wartości funkcji: a) f(x)= x3-5x2+3x - 2 f(![]()
) , f(0) b) f(x)= x2 - 2x + 6 f(![]()
)
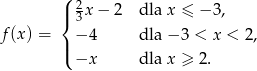
c) ![]()
f(![]()
) f( ![]()
) d) f(4), f(-5), f(2), f(0)
11. Znajdź wzór funkcji kwadratowej wiedząc, że : a) wierzchołkiem paraboli jest punkt (2;-6) i przechodzi ona
przez punkt ( 1;-4) b) miejscami zerowymi są liczby -3 i 4 i jej wykres przechodzi przez punkt (3;-12),
c) jej wykres przechodzi przez punkty: (0;4), (-1;1) i (2;2)
12. Podaj maksymalne przedziały monotoniczności funkcji: a) f(x) = -3x+2 b) f(x)= 12x -5 c) f(x)= ![]()
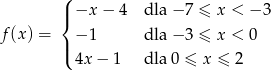
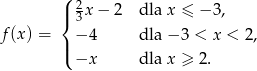
d) f(x)=3(x+5)2+2 e) ![]()
f) g)
13.Wyznacz zbiór wartości podanych obok funkcji : a) f(x)= 4x-5 b) y = x2+2x - 4 c) y =3(x+2)2-5
d) y= -(x - 2)(x+4) e) ![]()
f) 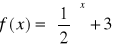
g) y= 4x+3 dla ![]()
h) f(x) = -x + 1 dla ![]()
i) f(x) = x2 - 6x + 2 dla ![]()
j) ![]()
k) ![]()
14 .Dla jakich wartości argumentów wartość funkcji a) y = -5x + 4 jest ujemna ? b) f(x) = x2 - 4 większa od 5 ?
c) f(x) = (x-3)2 jest równa 16 ? d) ![]()
jest równa 4 ? e) ![]()
jest mniejsza od 10 ?
f) f(x) = (x+5)(x-6) jest nieujemna ? g) ![]()
jest większa od 2 ? h) y = x2+4x+8 jest dodatnia ?
15. Wyznacz wartość największą i najmniejszą funkcji kwadratowej w podanym przedziale domkniętym:
a) ![]()
dla ![]()
b) ![]()
dla ![]()
c) ![]()
dla ![]()
16. Na podstawie wykresów funkcji podanych niżej określ: dziedzinę funkcji, zbiór wartości funkcji, miejsca
zerowe funkcji, maksymalne przedziały monotoniczności funkcji, znak funkcji oraz wartości ekstremalne funkcji
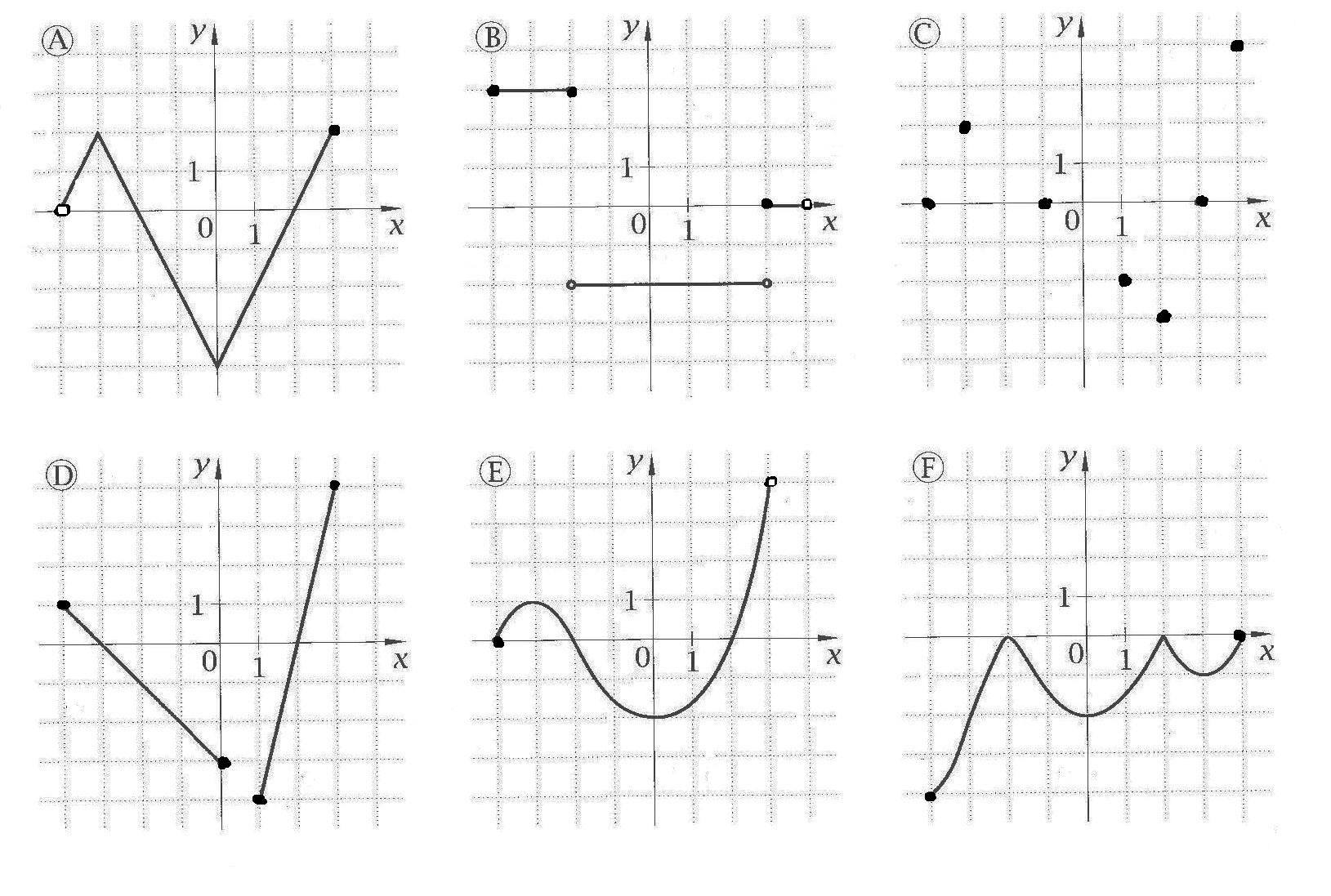
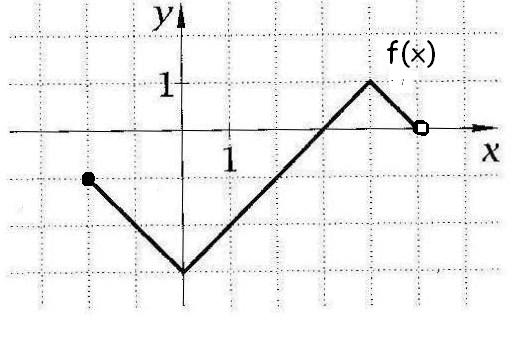
17. Na podstawie wykresu funkcji f(x) naszkicuj wykresy funkcji określonych wzorami:
a) y = f(x- 3) b) y = f(x) - 2 c) y = f(x+2) d) y = f(x) + 3
e) y = f(x + 2) - 4 f) y = f(x - 2)+3 g) y = - f(x) h) y = f(- x)
i) y = - f(x) + 2 j) y = - f(x- 3) + 2 k)* y =![]()
l*) y=![]()
m*) y=2f(x)
n*) y =-2 f(x) o*) y = ![]()
p*) y =![]()
- 3 r**) y=![]()
18. W jaki sposób należy przekształcić wykres funkcji f(x), aby otrzymać wykres funkcji g(x)?
a) f(x) = x2 g(x)=(x+3)2 b) f(x) = 3x2 g(x)=3(x-4)2 - 5 c) f(x) = x2 +3 g(x)= - x2 -3 d) f(x)=x+5 g(x)= -x+5
e) ![]()
![]()
f) ![]()
![]()
g) ![]()
![]()
h) ![]()
![]()
i) ![]()
![]()
j) ![]()
![]()
19. a) funkcja ![]()
ma miejsca zerowe -3 i 5, podaj miejsca zerowe funkcji ![]()
,
b) funkcja ![]()
przyjmuje wartości dodatnie dla ![]()
, dla jakich x funkcja ![]()
przyjmuje
wartości dodatnie?
c) funkcja ![]()
jest rosnąca dla ![]()
, dla jakich wartości x funkcja ![]()
+ 3 rośnie?
d) wykres funkcji![]()
przesunięto o 5 jednostek w lewo i 3 jednostki w górę , podaj wzór otrzymanej funkcji
e) wykres funkcji![]()
przesunięto o 7 jednostek w prawo a następnie przekształcono symetrycznie względem
osi x, podaj wzór funkcji otrzymanej w wyniku tych przekształceń.
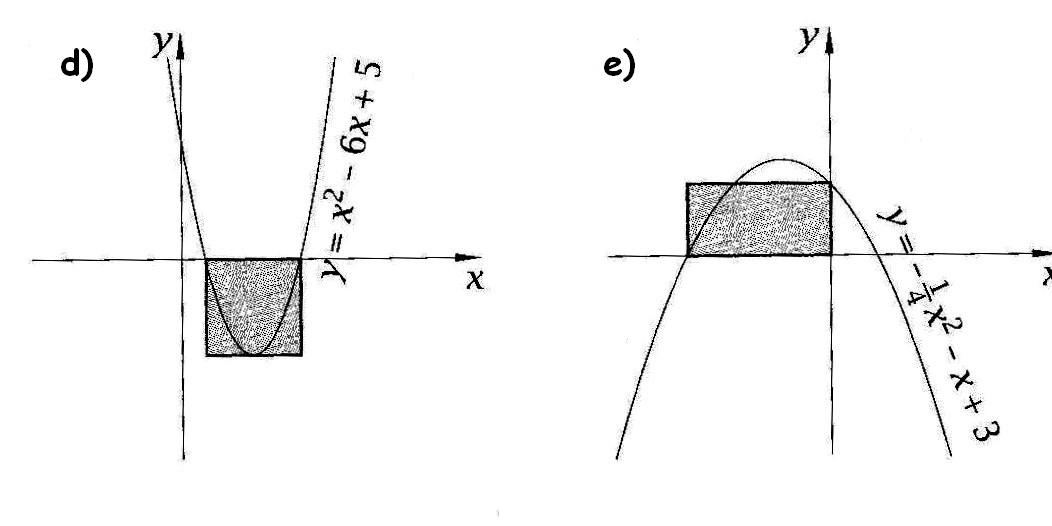
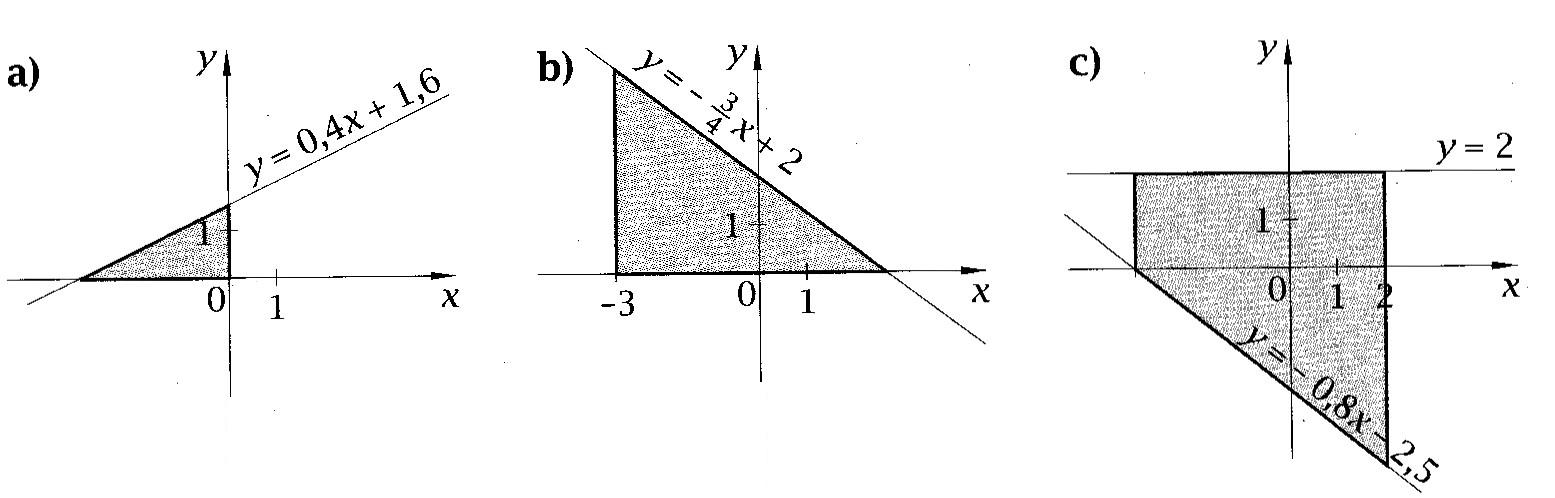
20.Oblicz pole zacieniowanej figury:
![]()
Wyszukiwarka