Temat: Reprezentacja pędów

Transformaty Fouriera amplitud

Rozpatrzymy harmonikę Fouriera
funkcji falowej

.

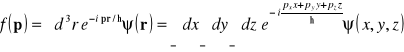
Przy jej pomocy można wyrazić funkcję falową, bo jest ona transformatą odwrotną

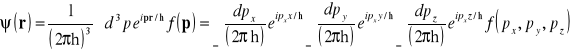
, (14.2a)

Za Baymem [1] przyjęliśmy, że transformata odwrotna jest proporcjonalna do czynnika
. Po podstawieniu do wzoru (14.2) postaci (14.1) harmoniki
otrzymamy tożsamość

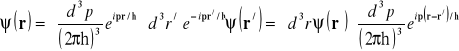
. (14.2b)

Zauważymy, że iloczyn
jest wielkością bezwymiarową, co gwarantuje, że obydwie strony równania (14.2b) są bezwymiarowe.

Jak widać całka po pędach (wektorach falowych) określa dystrybucję delta

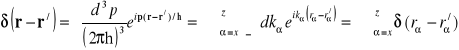
. (14.3)

14.2 Reprezentacja pędów

Wprowadzimy zapis

. (14.4a)

Rozpatrzymy amplitudę sprzężoną do
, zgodnie z jedną z własności iloczynu skalarnego i definicją (14.4a) mamy

. (14.4b)

Pokażemy, że harmonikę f(p) można także zapisać w postaci iloczynu
. Na podstawie równań (14.1) i (14.4b) i (13.16) mamy

. (14.5)

Zajmiemy się teraz relacją (14.2). Na podstawie wzorów (14.4a) i (14.5) możemy napisać

.

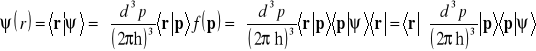
Zatem spełniony jest związek

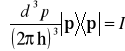
. (14.6)

Widzimy, że zbiór wektorów
parametryzowanych przez wartości składowych
wektora pędu
tworzy układ zupełny. Możemy zapisać wektory stanu i operatory wielkości fizycznych charakteryzujących cząstkę swobodną w tej bazie. Bę­dziemy mówili o wektorach stanu i macierzach operatorów w reprezentacji pędów.

Rozpatrzymy unormowany do jedności iloczyn skalarny
. Wstawimy pomiędzy wektory tego iloczynu jedynkę operatorową (14.6)

,

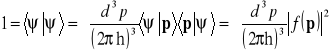
zatem

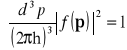
. (14.7)

Wielkość
jest prawdopodobieństwem znalezienia pędu cząstki w otoczeniu
o objętości
punktu p przestrzeni pędów. Zapiszemy zasadę superpozycji w reprezentacji pędów

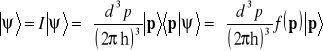
. (14.8)

14.3 Operatory wielkości fizycznych

Przy pomocy wektorów
wprowadzimy operator α-tej składowej pędu

. (14.9)

Ponieważ energia kinetyczna cząstki musi być wielkością skończona wartości własne każdego z operatorów

zawarte są w przedziale
. Zbadajmy jak działa operator pędu na dowolny wektor stanu

.

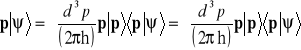
W ten sposób uzyskaliśmy postać spektralną operatora pędu

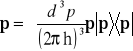
. (14.10)

Ponieważ wyniki pomiatu składowych pędu sa liczbami rzeczywistymi operator pędu jest hermitowski

.

Zapiszemy wektor stanu
w reprezentacji położeń

. (14.11)

Rozpatrzymy element macierzowy w reprezentacji położeń

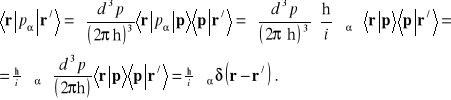
(14.12a)

Obecność dystrybucji
we wzorze (14.12a) mówi o tym, że mamy do czynienia z elementem diagonalnym. Tak więc „macierz” odpowiadająca w reprezentacji położeń operatorowi składowej pędu jest diagonalna, a wyrazy diagonalne są proporcjonalne do operato­rów różniczkowania

. (14.12b)

Znajdziemy operatorową postać równania Schrödingera (13.13) dla cząstki swobodnej nie poddanej działaniu pól zewnętrznych. W tym celu powrócimy do równania Schrödingera (13.11), którego prawą stronę można przekształcić

.

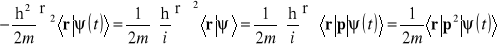
Jak widać dla cząstki swobodnej równanie Schrödingera (13.11) można zapisać w postaci nie­zależnej od wyboru reprezentacji

. (14.13)

Gdy cząstka znajduje się w polu potencjalnym do hamiltonianu
należy dodać jeszcze operator
, a więc całkowity operator Hamiltona cząstki ma postać

. (14.14)

Operator Hamiltona
ma odpowiednik klasyczny - funkcję Hamiltona
.

Rozpatrzymy niediagonalny element macierzowy operatora położenia

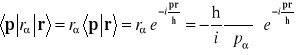
. (14.15)

Jak widać w reprezentacji pędów operator
-tej składowej operatora położenia proporcjonalny jest proporcjonalny do operatora różniczkowania po α-tej składowej pędu. Macierz odpowiadająca w reprezentacji pędów α-tej składowej operatora położenia cząstki jest diagonalna, nieznikające elementy są proporcjonalne do tego operatora różniczkowania po α-tej składowej pędu

. (14.16)

Element macierzowy
proporcjonalny jest do funkcji
operatora różniczkowania

. (14.17)

14.4 Ruch cząstki swobodnej

Założymy, że na cząstkę nie działają pola zewnętrzne. Przyjmijmy, że początkowo cząstka znajdowała się w stanie o określonym pędzie p:
. Zauważymy, że jest to wektor własny operatora Hamiltona. Nie trudno znaleźć wektor stanu cząstki w dowolnej chwili t

. (14.18)

Znajdziemy funkcję falową odpowiadającą wybranemu wektorowi stanu
w reprezentacji położeń

.

Ponieważ
mamy do czynienia ze stanem stacjonarnym, co nie powinno być niespodzianką ponieważ początkowo stan określał wektor
, czyli wektor własny operatora energii
, zatem cząstka miała określoną energię.

14.5 Ruch paczki falowej

Rozważymy ruch cząstki poruszającej się wzdłuż osi x. Niech w momencie czasu t=0 funkcja falowa ma postać

, (14.19)

gdzie
i
są funkcjami rzeczywistymi, ponadto
jest wielkością bezwymiarową. Niech funkcja
ma w otoczeniu punktu p₀ ostre maksimum o szerokości połówkowej
, np. można przyjąć, że ma ona postać

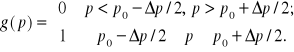
(14.20)

W momencie czasu t odpowiada jej funkcja falowa
, która po wykorzystaniu wzorów (10.32) i (14.4a) przyjmuje postać

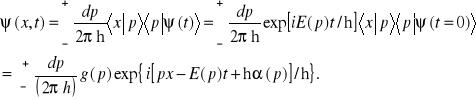
(14.21)

W momencie czasu t dla większości punktów osi x funkcja wykładnicza znajdująca się pod znakiem całki silnie oscyluje i nawet otoczenie punktu p₀, gdzie funkcja
jest duża, daje mały wkład, a więc całka określająca funkcję falową znika. Jednak gdy w pewnym przedziale pędów, do którego należy pęd p₀, faza wyrażenia podcałkowego

(14.22a)

zmienia się powoli to całka ta może być różna od zera. Jeżeli faza
jest powoli zmienną funkcją pędu to można ją rozłożyć w szereg potęgowy w
w otoczeniu p₀ i ograniczyć się do kilku pierwszych wyrazów

.(14.22b)

Dla małych
znikanie drugiego wyrazu szeregu zapewnia powolną zmienność
. Zatem przyjmijmy, że
, a to oznacza, że faza
ma w tym punkcie ekstremum. Z tego warunku znajdujemy zależność położenia x od czasu

, (14.23a)

gdzie

. (14.23)

Wielkość
ma wymiar prędkości natomiast
wobec bezwymiarowości α ma wymiar ilorazu
, czyli długości. Ponieważ rozważamy ruch cząstki swobodnej pochodna
jest prędkością p/m

.

W ogólnym przypadku, gdy prawo dyspersji różne jest od kwadratowego, pochodna energii po pędzie różni się od prędkości p/m. Pochodna
określa wektor prędkości grupowej - w naszym przypadku wektor o jednej składowej. Prędkość grupowa jest prędkością propagacji superpozycji (14.21) fal. Taka superpozycja nazywana jest paczką falową. Funkcja
określa skład spektralny funkcji falowej, dla tego nazywa się ona gęstością spektralną paczki. Dla gęstości spektralnej w postaci (14.20) otrzymamy

, (14.24)

gdzie

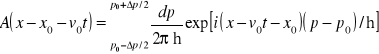
. (14.25)

Funkcja
zależy od czasu i współrzędnej x poprzez argument
. Ustalmy moment czasu t. Gdy
jest dużą wielkością to funkcja podcałkowa (14.25) silnie oscyluje dla wszystkich pędów należących do przedziału całkowania, w rezulta­cie funkcja
jest bardzo mała. Natomiast gdy
to funkcja podcałkowa dla pędów z przedziału
oscyluje słabo, a więc fale składające się na funkcję
interferują konstruktywnie. By konstruktywna interferencja miała miejsce zmiana
fazy
(14.22b) powinna w przedziale
spełniać nierówność

.

To oznacza, że gdy

mamy do czynienia z interferencją konstruktywną i z całą pewnością punkt x należy do paczki falowej. Zatem rozmiar liniowy paczki falowej
jest co najmniej równy
, a to oznacza, że rozmiar liniowy paczki
spełnia nierówność

.

Jak widać rozrzut
pędów fal dających wkład o całki (14.25) i rozmiar liniowy
paczki falowej spełniają nierówność

. (14.26)

Jest to nierówność nazywana nierównością Heisenberga dla jednowymiarowej paczki falowej. Można rozpatrzyć trójwymiarową paczkę falową, wtedy należy wprowadzić gęstość spektralną

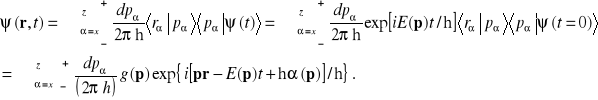
Gdy mamy do czynienia z paczką falową poruszająca się w przestrzeni prędkość grupowa jest wektorem o składowych

. (14.27)

Rozmiary paczki
w każdym z trzech kierunków
spełniają nierówności

. (14.28)

Trzy nierówności (14.28) są nierównościami Heisenberga dla trójwymiarowej paczki falowej. Podkreślmy - rozmiar liniowy
w kierunku α i rozrzut pędu w kierunku β
nie są ze sobą związane. Z nierówności (14.28) wynika, że jeżeli paczka falowa jest dobrze zlokalizowana, tj. gdy
,
to jej pęd jest całkowicie nieokreślony. Natomiast cząstka niezlokalizowana
ma ściśle określony pęd
. W granicy klasycznej gdy
ograniczenia na nieokreśloność położenia i pędu znikają.

Paczka falowa o prędkości grupowej
przebywa w obszarze
otaczającym punkt x przez interwał czasu
, stąd
. Lewa strona tej relacji jest równa w przybliżeniu
, natomiast prawa jest nie mniejsza od
. To oznacza, że nieokreśloność energii
związana z nieokreślonością pędu i charakterystyczny czas lokalizacji cząstki
spełniają nierówność rozważanego typu

. (14.29)

14.6 Kanoniczne reguły komutacji operatorów składowych położeń i pędów

Pokażemy, że składowe operatora położenia
i składowe operatora pędu
nie komutują spełniają związek podobny do nakładanego na nawiasy Poissona dla współrzędnych i pędów uogólnionych znanego z mechaniki klasycznej. W tym celu dla dowolnego wektora stanu
i dowolnego wektora własnego operatora położenia
rozpatrzymy element macierzowy
komutatora

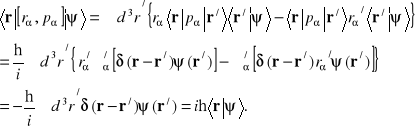
Ponieważ wektor
jest dowolny i na wektor wodzący r nie nałożyliśmy ograniczeń, dla każdej składowej α operatora położenia i operatora pędu słuszna jest relacja

. (14.30)

14.7 Nierówność Schwartza

Niech
będzie dowolnym wektorem stanu. Iloczyn
jest wielkością rzeczywistą (
) spełniającą nierówność

. (14.31)

Załóżmy, że
, gdzie
jest dowolnym parametrem. Przyjmijmy, że
. Wykorzystamy nierówność (14.31)

.

Wybierzemy

,

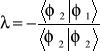
wtedy

, (14.32)

Po pomnożeniu obydwu stron nierówności (14.32) przez
otrzymamy nierówność Schwartza

. (14.33)

Równość ma miejsce wtedy i tylko wtedy gdy
, tj. gdy
, tzn. gdy wektory
są proporcjonalne. Normy wektorów
(j=1,2) spełniają nierówność

.

14.8 Nierówności Heisenberga

Podamy bardziej formalne wyprowadzenie nierówności Heisenberga, co wyjaśni ich sens, i jednocześnie uogólnimy je. Rozważymy parę hermitowskich, niekomutujących operatorów
(
,
,
). Niech
będzie wektorem własnym operatora
, natomiast
wektorem własnym operatora
. Odpowiednie wartości własne
są liczbami rzeczywistymi. Rozważymy amplitudę
. Kwadrat jej modułu jest prawdopodobieństwem zdarzenia polegającego na tym, że w przypadku układu będącego w stanie własnym
pomiar wielkości związanej z operatorem
da wartość własną β_j. Przyjmiemy, że ono nie znika
. Rozważymy średnie kwadratowe odchylenie
w dowolnym stanie

,
.

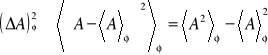
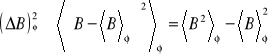
Średnie odchylenia kwadratowe znikają wtedy i tylko wtedy gdy
jest wektorem własnym operatora
albo
.

Zapiszemy średnie kwadratowe odchylenia w stanie
w postaci iloczynów skalar­nych

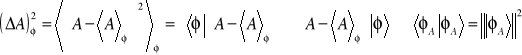
, (14.34a)

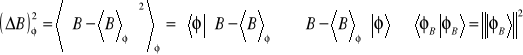
. (14.34b)

Wykorzystamy nierówność Schwartza

. (14.35)

Zbadajmy wyraz
. Przekształcimy go wykorzystując własność hermitowskości obydwu operatorów

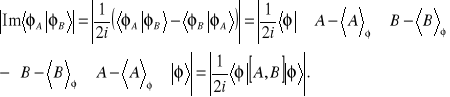
Ostatecznie

. (14.36a)

Gdy

. (14.36b)

Ponieważ
,
, więc ostatecznie otrzymujmy uogólnioną nierówność Heisenberga dla odchyleń standardowych średnich wartości dwóch niekomutujących operatorów

. (14.37)

Podkreślmy, nierówność Heisenberga (14.36a) dotyczy odchyleń standardowych i nie wymaga aby pomiary średnich wartości niekomutujących operatorów były jednoczesne. Ponieważ jak dotąd nie znaleziono operatora czasu nierówność (14.29) nie ma takiego samego statusu jak nierówności Heisenberga (14.36).

14.8 Stany z najmniejszą nieokreślonością

Nierówność Schwartza (14.36) sprowadza się do równości gdy wektory ją spełniające są proporcjonalne. Znajdziemy postać funkcji falowej, dla której nierówność Heisenberga dla składowych operatora położenia i składowych operatora pędu sprowadza się do równości, czyli jest minimalna [2]. Takie stany możemy uznać za najbardziej klasyczne stany kwan­towe. Przyjmiemy współczynnik proporcjonalności w postaci

. (14.38)

Wyprowadzimy równanie różniczkowe dla funkcji falowej
. W tym celu pomnożymy obydwie strony równania (14.38) przez wektor bra

.

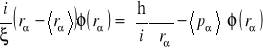
Otrzymaliśmy nieskomplikowane równanie różniczkowe, którego rozwiązaniem jest funkcja

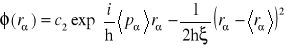
. (14.39)

Stałe całkowania określimy z warunku normowania funkcji falowej

,

i by całka
była równa zadanemu średniemu kwadratowemu odchyle­niu

.

Z tych warunków znajdujemy
,
. Wybierzemy fazę stałej
tak, aby była ona wielkością rzeczywistą, wtedy

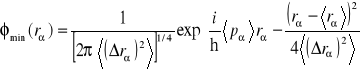
. (14.40)

W ten sposób otrzymaliśmy w reprezentacji położeń jawną postać funkcji falowej o naj­mniej­szej nieoznaczoności. Gdy układ znajduje się w stanie
to wielokrotne pomiary współrzędnej r_α daje wynik równy
, wielokrotne pomiary składowej α pędu dają
. Średnie kwadratowe odchylenie składowej α położenia jest zadane. Natomiast zgodnie z zasadą nieoznaczoności średnie kwadratowe odchylenie składowej α pędu wyraża się przez

.

Pierwszy czynnik w wykładniku funkcji (14.40) przypomina falę płaską. Zauważymy, że prawdopodobieństwo znalezienia cząstki w przedziale
proporcjonalne jest do funkcji rozkładu Gaussa

.

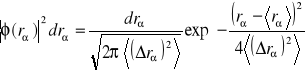
W zupełnie podobny sposób (albo dokonując przekształcenia Fouriera funkcji (14.40)) można w reprezentacji pędów znaleźć funkcję falową z stanu najmniejszą nieokreślonością

.

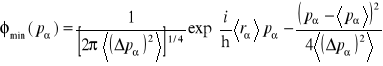
14.10 Prędkość fazowa

Wprowadziliśmy prędkość grupową. Z tą prędkością poruszają się paczki falowe, a więc przenoszone są wielkości fizyczne, np. energia i pęd. Wprowadzimy jeszcze prędkość fazową. Rozpatrzymy warunek stałości fazy fali płaskiej

.

Określa on rodzinę płaszczyzn prostopadłych do wektora p (Rys. 14.1)

Ta płaszczyzna porusza się z prędkością fazową

. (14.41)

Prędkość fazowa jest wielkością skalarną. Obliczymy rzut prędkości grupowej (14.27) na kierunek propagacji fali płaskiej

.

Taka nierówność jest słuszna także gdy prawo dyspersji nie jest kwadratowe.

Literatura:

[1] G. Baym, Lectures on Quantum Mechanics, Benjamin, Reading, Mass., 1974, R. 3.

[2] W. H. Louisell, Radiation and Noise in Quantum Electronics, McGrow-Hill, New York, 1964, § 1.13.

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

---