Wykład Matematyka doc. Andrzej Drozdowicz
Własności funkcji jednej zmiennej
Parzystość i nieparzystość
Określoność
Monotoniczność
Ograniczoność
Różnowartościowość y=f(x) jest różnowartościowa w zbiorze X jeżeli dla każdego x1 x2 zawierającego się w X f(x1)≠f(x2)
Np.
Funkcja złożona jeżeli funkcja f odwzorowuje zbiór X w Y a funkcja g odwzorowuje zbiór Y w Z to funkcja h(x)=g(f(x)) odwzorowuje zbiór X w Z. Funkcję taką nazywamy złożoną przy czym f jest funkcją wewnętrzną a g funkcją zewnętrzną
Np.
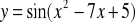
Funkcja odwrotna jest to przyporządkowanie określające na elementach zbioru wartości funkcji różnowartościowej f pewną nową funkcję, dla której zbiór wartości jest zbiorem X nazywamy funkcję odwrotną i oznaczamy f-1. Funkcje f i f-1 stanowią parę funkcji wzajemnie odwrotnych
y=2x+4
2x=y-4
x=0,5y-2 funkcja odwrotna do wyjściowej
y=0,5x-2
Wykres funkcji odwrotnej do wykresu danej funkcji jest symetryczny względem prostej y=x
![]()
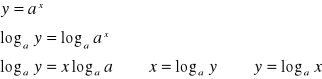
Funkcja logarytmiczna i wykładnicza stanowią parę funkcji odwrotnych
Logarytm przy podstawi a z liczby dodatniej b nazywamy potęgę, do której należy podnieść podstawę a aby otrzymać wyrażenie logarytmowane
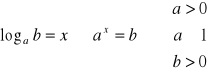
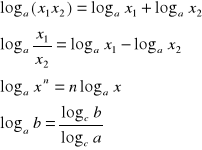
WAŻNE !!!
Funkcje cyklometryczne są to funkcje odwrotne do funkcji trygonometrycznych
Rozważmy funkcję ![]()
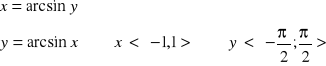
Tabela wartości podstawowych dla tej funkcji to:
x |
-1 |
|
|
|
0 |
|
|
|
1 |
y |
|
|
|
|
0 |
|
|
|
|
Sin i arc sin to funkcje wzajemnie odwrotne
Rozważmy ![]()
![]()
Tabela wartości podstawowych funkcji podobnie jak dla y=sinx
Rozważmy ![]()
![]()
x |
-∞ |
|
-1 |
|
0 |
|
1 |
|
∞ |
y |
|
|
|
|
0 |
|
|
|
|
Rozważmy ![]()
![]()
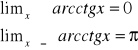
Przestrzeń metryczna
Zbiór X nazywamy przestrzenią metryczną, jeśli każdej parze jego elementów (punktów) P(p1,p2,…,pn) i Q(q1,q2,…,qn) przyporządkowana jest jednoznacznie liczba rzeczywista nieujemna d(P,Q) spełniająca warunki:
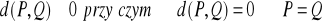
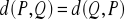
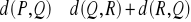
jest to nierówność trójkąta
Wielkość d(P,Q) jest metryką przestrzeni metrycznej
Przykłady:
Niech ![]()
będzie ciągiem przestrzeni p
Mówimy, że punkt p0 jest granicą ciągu pn lub, że ciąg pn jest zbieżny do p0 co zapisujemy
![]()
, jeżeli odległości d(pn,p0) stanowią ciąg zbieżny do 0
Jeżeli ![]()
jest ciągiem punktów na osi liczbowej R to ![]()
xn=an x0=g
![]()
Przykłady liczenia granic - zajęcia wyrównawcze
Pewne ciągi specjalne:
Jest to liczba niewymierna przestępna tzn. taka, że nie może być pierwiastkiem żadnego równania algebraicznego o wykładnikach wymiernych
Matematyka wykład doc. Andrzej Drozdowicz 10.11.2009r.
Wyszukiwarka