1.Cel ćwiczenia.
Badanie elektromagnetycznych drgań wymuszonych w obwodzie RLC.
2.Podstawy fizyczne,
Drgania są zjawiskiem powszechnie występującym w przyrodzie i technice. W zjawisku tym stan fizyczny układu drgającego opisywany jest przez wielkości fizyczne zależne okresowo od czasu. Najważniejszym a także najprostszym rodzajem drgań są tzw. drgania harmoniczne, w których zależność od czasu można opisać funkcjami sinus lub cosinus.
Swobodne drgania harmoniczne wykonuje układ fizyczny, do którego została jednorazowo dostarczona pewna porcja energii i nie ma dalszego wpływu otoczenia na układ.
Jeśli na układ drgający działa harmoniczne wymuszenie, dostarczające okresowo energię, to mimo występowania tłumienia liniowego zachodzą ustalone drgania wymuszone.
Elektromagnetyczne drgania wymuszone można zaobserwować w obwodzie RLC (zawierającym cewkę o indukcyjności L, kondensator o pojemności C oraz opornik o oporności R) do którego zostało dołączone źródło napięcia sinusoidalnego.
Stan fizyczny takiego układu opisuje II prawo Kirchoffa:
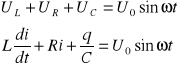
Po podzieleniu przez L i podstawieniu
![]()
![]()
![]()
gdzie β-współczynnik tłumienia, ![]()
-częstość drgań swobodnych, otrzymujemy równanie elektromagnetycznych drgań wymuszonych
![]()
Ponieważ napięcie wymuszające jest sinusoidalną funkcją czasu, to rozwiązania tego równania poszukujemy w postaci funkcji ![]()
, zatem ładunek na kondensatorze będzie się zmieniać sinusoidalnie z częstością taką jak częstość napięcia wymuszającego oraz, że będzie przesunięty w fazie o ![]()
względem tego napięcia.
Wzory określające amplitdę napięcia łądunku ![]()
i przesunięcie fazowe ![]()
są następującej postaci:
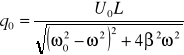
![]()
Przy ustalonych parametrach R,L,C, a więc również ![]()
i ![]()
amplituda ładunku oraz przesunięcie fazowe są funkcjami częstości ![]()
napięcia wymuszającego.
Amplituda ładunku na kondensatorze osiąga wartość maksymalną dla częstości wymuszania ![]()
określonej wzorem
![]()
gdzie ![]()
Zjawisko wymuszania drgań z taką częstością przy której amplituda drgań osiąga wartość maksymalną nazywamy rezonansem. Rezonans w obwodzie RLC zachodzi przy częstości wymuszania ![]()
zwanej częstością rezonansową , gdy współczynnik tłumienia β jest mniejszy od wartości granicznej ![]()
.
Amplitudę drgań i przesunięcie fazowe w stanie rezonansu można wyrazić wzorami:
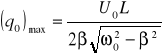
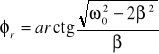
Szczególny przypadek rezonansu występuje w przypadku gdy współczynnik tłumienia β=0.
Dla takiego układu rezonans zachodzi przy częstości wymuszania równej częstości drgań własnych ![]()
i objawia się wzrostem amplitudy do nieskończoności oraz przesunięciem fazowym ![]()
.
Wzory opisujące kolejno amplitudę drgań i przesunięcie fazowe dla dowolnej częstości wymuszania, częstość rezonansową oraz amplitudę drgań i przesunięcie fazowe w stanie rezonansu przyjmują następującą postać:
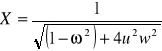
![]()
![]()
![]()
![]()
Napięcie na kondensatorze.
![]()
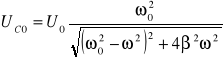
![]()
Wstanie rezonansu, czyli dla częstości wymuszania równej ![]()
, amplituda napięcia na kondensatorze osiąga wartość maksymalną:
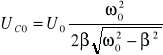
dla ![]()
a przesunięcie fazowe względem napięcia wymuszającego wynosi
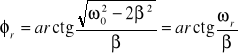
Współczynnik dobroci
Dobroć układu drgającego - określa ile razy amplituda ![]()
ustalonych drgań wymuszonych w stanie rezonansu jest większa od amplitudy z dala od rezonansu.
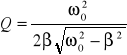
W przypadku dużego tłumienia, tzn. gdy współczynnik tłumienia zbliża się do wartości granicznej 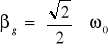
dobroć maleje do jedności.
3.Metoda pomiarowa i układ pomiarowy.
rys.1
Celem ćwiczenia jest badanie drgań elektromagnetycznych w obwodzie RLC wymuszonych przez sinusoidalne zmienne napięcie generatora.
W układzie pomiarowym na rys.1 znajduje się generator, miernik częstotliwości, oscyloskop i płytka pomiarowa umożliwiająca połączenie elementów R,L i C obwodu oraz dołączenie generatora i oscyloskopu.
Metoda polega na wykorzystaniu oscyloskopu i miernika częstotliwości.
Generator dostarcza do obwodu RLC napięcie sinusoidalne o ustalonej amplitudzie i regulowanej częstotliwości. Dokładny odczyt częstotliwości umożliwia miernik częstotliwości podłączony równolegle do wyjścia z generatora. Napięcie z generatora jest podawane na płytki odchylania poziomego (wejście X) a napięcie z kondensatora na płytki odchylania pionowego (wejście Y).
![]()
![]()
W wyniku składania dwóch drgań harmonicznych o jednakowych częstotliwościach na ekranie oscyloskopu powstaje elipsa, której kształt zależy od amplitud oraz od przesunięcia fazowego.
4.Przebieg ćwiczenia.
a. Pierwsza seria pomiarowa.
seria I l=1,58 c=30 r=200
cz |
a |
b |
d |
|
sinkata |
kat |
w |
uc0 |
ug0 |
X |
7,83 |
3,6 |
1,4 |
1,9 |
|
0,3889 |
0,3994 |
0,38697 |
1,8 |
1,9 |
0,9474 |
10 |
3,8 |
1,8 |
1,9 |
|
0,4737 |
0,4935 |
0,49421 |
1,9 |
1,9 |
1,0000 |
14,41 |
3,9 |
2,4 |
1,9 |
|
0,6154 |
0,6629 |
0,71216 |
1,95 |
1,9 |
1,0263 |
16,5 |
3,6 |
3 |
1,8 |
|
0,8333 |
0,9851 |
0,81545 |
1,8 |
1,8 |
1,0000 |
17,91 |
3,6 |
3,2 |
1,8 |
|
0,8889 |
1,0949 |
0,88513 |
1,8 |
1,8 |
1,0000 |
18,55 |
3,4 |
3,4 |
1,8 |
|
1,0000 |
1,5708 |
0,91676 |
1,7 |
1,8 |
0,9444 |
19,78 |
3,4 |
3,2 |
1,8 |
|
0,9412 |
1,9155 |
0,97755 |
1,7 |
1,8 |
0,9444 |
25,1 |
2,8 |
2,6 |
1,6 |
|
0,9286 |
1,9510 |
1,24047 |
1,4 |
1,6 |
0,8750 |
26,52 |
2,6 |
2,4 |
1,6 |
|
0,9231 |
1,9656 |
1,31064 |
1,3 |
1,6 |
0,8125 |
30,02 |
2,2 |
1,8 |
1,6 |
|
0,8182 |
2,1833 |
1,48362 |
1,1 |
1,6 |
0,6875 |
34,47 |
1,6 |
1,4 |
1,7 |
|
0,8750 |
2,0762 |
1,70354 |
0,8 |
1,7 |
0,4706 |
39,67 |
1,4 |
1 |
1,8 |
|
0,7143 |
2,3460 |
1,96053 |
0,7 |
1,8 |
0,3889 |
45,32 |
1 |
0,6 |
1,9 |
|
0,6000 |
2,4981 |
2,23976 |
0,5 |
1,9 |
0,2632 |
51,1 |
0,8 |
0,4 |
1,9 |
|
0,5000 |
2,6180 |
2,52541 |
0,4 |
1,9 |
0,2105 |
55,48 |
0,6 |
0,4 |
1,9 |
|
0,6667 |
2,4119 |
2,74187 |
0,3 |
1,9 |
0,1579 |
60,77 |
0,6 |
0,2 |
2 |
|
0,3333 |
2,8018 |
3,00331 |
0,3 |
2 |
0,1500 |
65,86 |
0,6 |
0,2 |
2 |
|
0,3333 |
2,8018 |
3,25486 |
0,3 |
2 |
0,1500 |
70,87 |
0,4 |
0,2 |
2 |
|
0,5000 |
2,6180 |
3,50246 |
0,2 |
2 |
0,1000 |
75,38 |
0,4 |
0,1 |
2 |
|
0,2500 |
2,8889 |
3,72535 |
0,2 |
2 |
0,1000 |
107,08 |
0,5 |
0,1 |
2 |
|
0,2000 |
2,9402 |
5,29199 |
0,25 |
2 |
0,1250 |
Seria II L=1,85 C=30 r=200
|
a |
b |
d |
|
sinkata |
kat |
w |
uc0 |
ug0 |
X |
7,88 |
4,2 |
0,5 |
1,9 |
|
0,1190 |
0,1193 |
0,38944 |
2,1 |
1,9 |
1,1053 |
18,05 |
6,4 |
3,6 |
1,6 |
|
0,5625 |
0,5974 |
0,89205 |
3,2 |
1,6 |
2,0000 |
20,01 |
6,9 |
5,2 |
1,4 |
|
0,7536 |
0,8536 |
0,98891 |
3,45 |
1,4 |
2,4643 |
22,11 |
7 |
6,8 |
1,2 |
|
0,9714 |
1,3312 |
1,09270 |
3,5 |
1,2 |
2,9167 |
23,19 |
6,8 |
6,8 |
1,2 |
|
1,0000 |
1,5708 |
1,14607 |
3,4 |
1,2 |
2,8333 |
23,84 |
6,5 |
6,4 |
1,2 |
|
0,9846 |
1,3952 |
1,17820 |
3,25 |
1,2 |
2,7083 |
24,49 |
6 |
5,4 |
1,3 |
|
0,9000 |
1,1198 |
1,21032 |
3 |
1,3 |
2,3077 |
25,77 |
5,6 |
4,7 |
1,4 |
|
0,8393 |
0,9960 |
1,27358 |
2,8 |
1,4 |
2,0000 |
28,19 |
4,5 |
3 |
1,7 |
|
0,6667 |
0,7297 |
1,39318 |
2,25 |
1,7 |
1,3235 |
30,05 |
3,7 |
2,1 |
1,8 |
|
0,5676 |
0,6035 |
1,48510 |
1,85 |
1,8 |
1,0278 |
35,55 |
2,4 |
1 |
1,9 |
|
0,4167 |
0,4298 |
1,75691 |
1,2 |
1,9 |
0,6316 |
40,31 |
1,8 |
0,6 |
1,9 |
|
0,3333 |
0,3398 |
1,99216 |
0,9 |
1,9 |
0,4737 |
45,48 |
1,2 |
0,4 |
2 |
|
0,3333 |
0,3398 |
2,24766 |
0,6 |
2 |
0,3000 |
50,42 |
0,9 |
0,2 |
2 |
|
0,2222 |
0,2241 |
2,49180 |
0,45 |
2 |
0,2250 |
55,09 |
0,8 |
0,1 |
2 |
|
0,1250 |
0,1253 |
2,72260 |
0,4 |
2 |
0,2000 |
60,35 |
0,6 |
0,1 |
2 |
|
0,1667 |
0,1674 |
2,98255 |
0,3 |
2 |
0,1500 |
65,81 |
0,4 |
0 |
2 |
|
0,0000 |
0,0000 |
3,25239 |
0,2 |
2 |
0,1000 |
70,06 |
0,4 |
0 |
2 |
|
0,0000 |
0,0000 |
3,46243 |
0,2 |
2 |
0,1000 |
75,14 |
0,3 |
0 |
2 |
|
0,0000 |
0,0000 |
3,71349 |
0,15 |
2 |
0,0750 |
81,95 |
0,2 |
0 |
2 |
|
0,0000 |
0,0000 |
4,05005 |
0,1 |
2 |
0,0500 |
Seria III l=1,58 c=1,3 r=200
|
a |
b |
d |
|
sinkata |
kat |
w |
uc0 |
ug0 |
X |
10,3 |
4,4 |
0,6 |
4,3 |
|
0,1364 |
0,1368 |
0,12837 |
4,4 |
4,3 |
1,0233 |
25,01 |
4,7 |
0,8 |
4,4 |
|
0,1702 |
0,1710 |
0,31171 |
4,7 |
4,4 |
1,0682 |
39,98 |
4,9 |
1 |
4,4 |
|
0,2041 |
0,2055 |
0,49829 |
4,9 |
4,4 |
1,1136 |
60,38 |
6,1 |
1,2 |
4,4 |
|
0,1967 |
0,1980 |
0,75255 |
6,1 |
4,4 |
1,3864 |
78,98 |
8,8 |
2,2 |
4,4 |
|
0,2500 |
0,2527 |
0,98437 |
8,8 |
4,4 |
2,0000 |
94,3 |
12,6 |
7,6 |
4,4 |
|
0,6032 |
0,6475 |
1,17531 |
12,6 |
4,4 |
2,8636 |
101,58 |
15,4 |
12,8 |
4 |
|
0,8312 |
0,9812 |
1,26604 |
15,4 |
4 |
3,8500 |
107,18 |
6,8 |
6,6 |
4 |
|
0,9706 |
1,3277 |
1,33584 |
6,8 |
4 |
1,7000 |
108,3 |
6,4 |
6 |
3,9 |
|
0,9375 |
1,2154 |
1,34980 |
6,4 |
3,9 |
1,6410 |
111,15 |
6,4 |
6,4 |
3,9 |
|
1,0000 |
1,5708 |
1,38532 |
6,4 |
3,9 |
1,6410 |
124,15 |
4 |
3 |
4,3 |
|
0,7500 |
2,2935 |
1,54734 |
4 |
4,3 |
0,9302 |
145,39 |
2,4 |
1,6 |
4,5 |
|
0,6667 |
2,4119 |
1,81207 |
2,4 |
4,5 |
0,5333 |
180,03 |
2,4 |
1,2 |
4,8 |
|
0,5000 |
2,6180 |
2,24380 |
2,4 |
4,8 |
0,5000 |
212,18 |
1,8 |
0,7 |
4,9 |
|
0,3889 |
2,7422 |
2,64450 |
1,8 |
4,9 |
0,3673 |
230,35 |
1,4 |
0,5 |
5,2 |
|
0,3571 |
2,7764 |
2,87097 |
1,4 |
5,2 |
0,2692 |
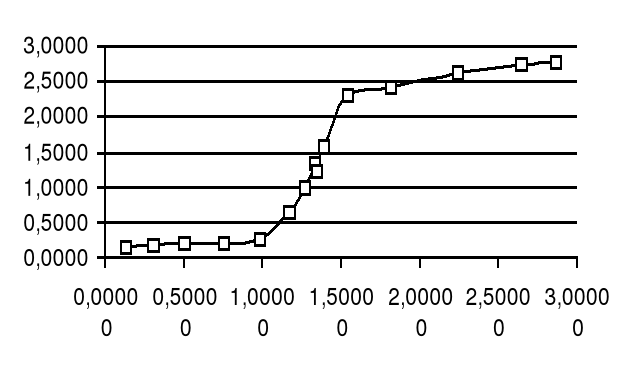
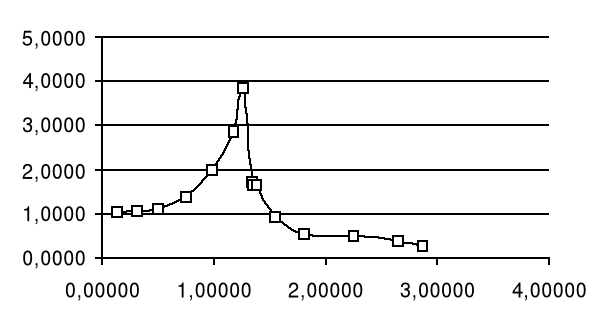
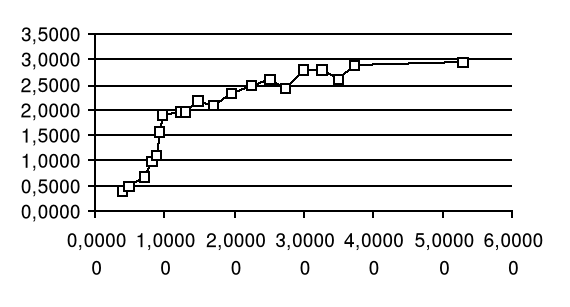
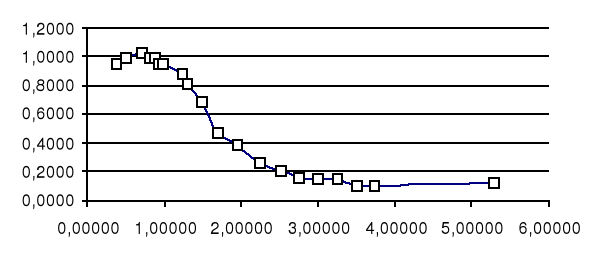
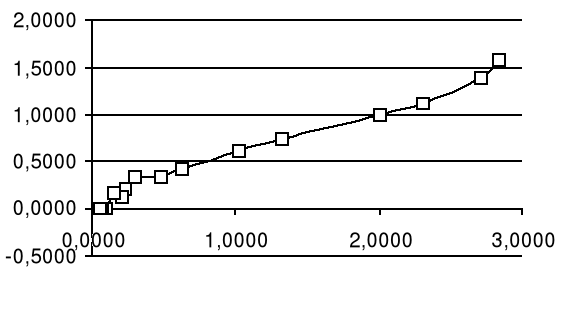
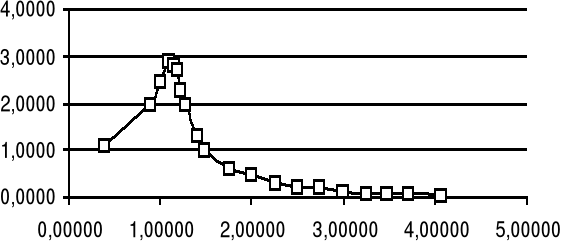
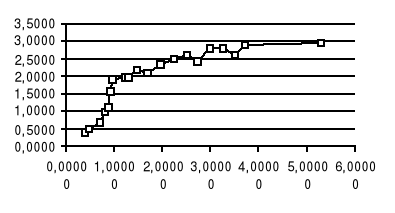
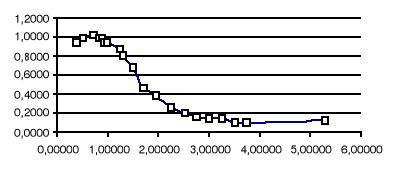
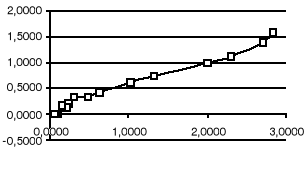
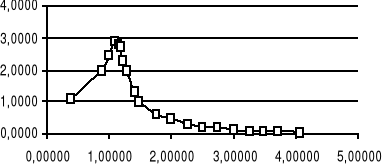
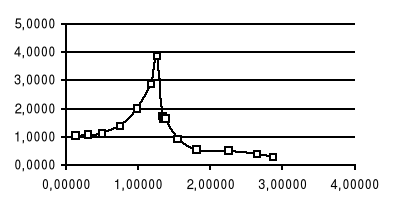
Nasz zespół otrzymał następujące wyniki które obrazują powyższe wykresy. Z nich można odczytać szerokość rezonansu, która w przybliżeniu wynosi dla kolejnych serii :
1,5; 1,7 sr, vr=14,41
1,5; 1,6 sr 1,55 vr=22,11
1,7; 0,5 sr, vr=101,58
zatem względna szerokość rezonansu to
0,11
0,07
0,01
Dla naszego doświadczenia otrzymaliśmy następujące wartości doświadczalne jak i teoretyczne :
teoretyczne:
L |
C |
R |
w 0 |
0 |
β |
Ω r |
v r |
Q |
0,00158 |
0,00000003 |
200 |
145248,2 |
23116,973 |
63291,14 |
114391,913 |
179686,4 |
1,27 |
0,00158 |
0,00000003 |
37 |
145248,2 |
23116,973 |
11708,86 |
144301,253 |
226667,9 |
6,22 |
0,00158 |
1,3E-09 |
200 |
697749,9 |
111050,34 |
63291,14 |
691985,101 |
1086968 |
5,53 |
doświadczalne :
L |
C |
R |
w 0 |
0 |
β |
Ω r |
v r |
Q |
0,00158 |
0,00000003 |
200 |
145248,2 |
1848000,0 |
91849,14 |
114391,913 |
144100 |
1,3027 |
0,00158 |
0,00000003 |
37 |
145248,2 |
22240,000 |
10662,86 |
144301,253 |
226667,9 |
6,6585 |
0,00158 |
1,3E-09 |
200 |
697749,9 |
102500,34 |
63291,14 |
691985,101 |
1015868 |
5,3132 |
Błąd ![]()
obliczyliśmy korzystając z metody różniczki logarytmicznej:
![]()
,
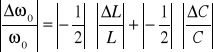
,
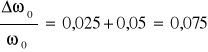
,
![]()
,
=10,55 kHz
=52,33 kHz
Błąd ![]()
0:
![]()
![]()
,
=23,37 kHz
=111,05 kHz
Błąd ![]()
obliczamy korzystając z metody różniczki logarytmicznej:
![]()
,
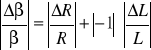
,
![]()
,
![]()
,
=1756 =9493
Błąd ![]()
obliczamy korzystając z metody różniczki zupełnej:
![]()
,
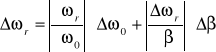
,
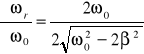
,
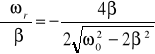
,
![]()
=24,23
= 53,45,
Obliczamy błąd ![]()
:
![]()
,
Błąd ![]()
obliczamy korzystając z metody różniczki zupełnej:
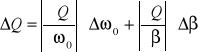
,
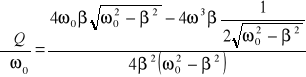
,
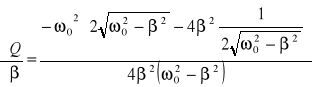
,
![]()
,
Błąd ![]()
obliczyliśmy korzystając z metody różniczki zupełnej:

,
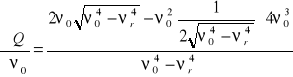
,
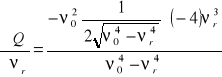
,
![]()
,
Błąd ![]()
obliczyliśmy korzystając z metody różniczki zupełnej:
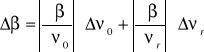
,
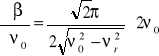
,
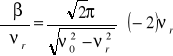
,
![]()
Wnioski
Otrzymane przez mój zespół wyniki mieszczą się w normie i są obarczone błędami mniejszymi niż 10 % wartości co należy uznać za wynik mieszczący się w granicach błędu. Błędy występujące w naszych badaniach są spowodowane brakiem doświadczenia w podobnych pomiarach, niedokładnością urządzeń pomiarowych oraz zawodnością aparatury pomiarowej. Pomiary 3 serii pomiarowej zostały przez mój zespół wykonane ponownie ze względu na duże błędy otrzymane za pierwszym razem co uniemożliwiło oddanie sprawozdania w pierwszych terminach. Sposób przeprowadzenia pomiarów należy jednak uznać za poprawny. Jednak należało by zwiększyć ilość punktów pomiarowych aby otrzymać pełne wykresy amplitud od zredukowanej częstości drgań. Gdyż przewidywanie wykresów wprowadza duży błąd do naszego ćwiczenia.

Wyszukiwarka