Wykład6
T: Wybrane charakterystyki funkcji produkcji
Def
Krańcowa wydajność i-tego nakładu w wektorze nakładów x nazywamy
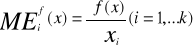
ME- marginal efficiency
Definicja
Elastyczność produkcji względem i-tego nakładu w wektorze x nazywamy wielkość
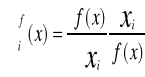
Mówi o ile % w przybliżeniu wzrośnie produkcja jeżeli i-ty nakład w wektorze x wzrośnie o 1%
Definicja
Krańcowa stopa substytucji i-tego nakładu przez j-ty nakład nazywamy
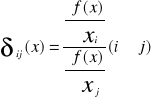
Mówi o jaką ilość nakładu j należy zastąpić w wektorze x jednostkowy spadek nakładu i aby wielkość produkcji nie zmieniła się
Definicja
Elastyczność substytucji i-tego nakładu przez j-ty nakład nazywamy
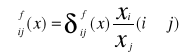
Mówi o ile % powinien zwiększyć się j-ty nakład w wektorze x, aby przy zmniejszeniu i-tego nakładu o 1% wielkość produkcji się nie zmieniła
T: Izokwanty funkcji produkcji
F: Rk+R1+ (funkcja produkcji) .
y0-nieujemna liczba rzeczywista .
y0≥0
Definicja
Zbiór postaci:
![]()
Nazywamy izokwantą (funkcji) produkcji
Przykład funkcji produkcji .
F:R2+R1+
Y=f(x)=f(x1, x2)
Q= f (K,L)
Q-produkcja
K-kapitał
L-praca
Definicja
Technicznym uzbrojeniem pracy nazywamy iloraz:
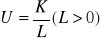
Funkcja produkcji Cobba-Douglasa (1927-28)
Funkcja produkcji f:R2+R1+ spełniająca warunki 1-4 oraz warunek:
Krańcowa stopa substytucji pracy przez kapitał zależy wyłącznie od technicznego uzbrojenia pracy i jest liniową, rosnącą, funkcją tego uzbrojenia czyli:
![]()
Ma postać
![]()
W której: A>0,
![]()
![]()
Są parametrami
parametr wydajności, uwzględnia postęp techniczny (techniczno-organizacyjny)
Parametry α i β są odpowiednio:
-elastycznością produkcji Q względem kapitału K oraz elastycznością produkcji Q względem pracy L
Funkcja Cobba-Douglasa jest funkcją dodatnio jednorodną stopnia r=β+γ β+γ≤1
r- parametr efektu skali
W przypadku gdy współczynnik efektu skali r=1 można wyprowadzić następujące zależności:
a)w-wydajność pracy
![]()
w=w(u)=Anβ
b) tzw. Efektywność kapitału od technicznego uzbrojenia pracy
![]()
![]()
e=e(u)=Auγ
![]()
A>0
α1, α2,... αk>0
Funkcja produkcji CES(1962)
(Constant Elasticity of Substitution)
SMAC-pierwsza nazwa (1961) od nazwisk 4 autorów
Funkcja produkcji f:R2+R1+ spełniająca warunki 1-4 oraz warunek 5I:
Krańcowa stopa substytucji pracy przez kapitał jest potęgową funkcją technicznego uzbrojenia pracy czyli:
![]()
Gdzie α i δ>0 ma postać
![]()
Gdzie A>0
![]()
Elastyczność krańcowej stopy substytucji pracy przez kapitał względem techicznego uzbrojenia pracy u jest stałą.
![]()
Funkcja produkcji Cobba-Douglasa jest szczególnym przypadkiem funkcji CES.
![]()
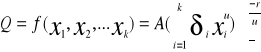
A>0
T:Elementy teorii przedsiębiorstwa
Przedsiębiorstwo w warunkach doskonałej konkurencji
Założenia:
Przedsiębiorstwo wytwarza 1 towar, zużywając w tym celu k innych towarów (nakłady, czynniki produkcji)
Działalność produkcyjną opisuje skalarna k czynnikowa funkcja produkcji .
Y=f(x) y=f(x1, x2,..xk) f: Rk+R+
3. Przypisujemy, że jedynym celem przedsiębiorstwa jest max. Zysku
4.Przedsiębiorstwo nie ma wpływu na ceny towarów
5.Przed. Nie ma problemu ze zbytem produkcji
6.Pozostałe działające na rynku przeds. Są w stanie natychmiast zaspokoić zmieniające się zapotrzebowanie producenta na towary będące nakładami
Zadanie1
Wyznaczyć wektor nakładów x tak aby,
Pf(x)-<v,x>max (1)
Przy ograniczeniach
x ≥ Θ (2)
gdzie:
p-cena wytworzonego dobra
v= (v1,...vk) wektor nakładów
Twierdzenie
Jeżeli funkcja produkcji f spełnia warunki 1-3 a ceny p i v spełniają warunki:
p>0
![]()
to:
istnieje jeden wektor x*>Θ maksymalizujący dochód
wektor ten spełnia układ równań
![]()
Wykład7
τ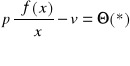
(x,p,v)=Θ (**)
Jeżeli f∈C2Df to rozwiązanie układu (**) można w otoczeniu każdego punktu
(x,p,v)> Θ przedstawić jako funkcję:
x=ξ(p,v)
Wynika to z tzw. Twierdzenia o funkcjach uwikłanych
Funkcja produkcyjnego popytu na towaru ξ(ksi)
ξ=(ξ1, ξ2,... ξk)
Funkcja ksi wyraża zależność optymalnego popytu x na towary od ceny p towaru wytwarzanego i cen v nakładów.
ξ- ma ciągłe pochodne cząstkowe w otoczeniu każdego punktu (p,v)> Θ-jest jednorodne stopnia zerowgo
ξ(λp, λv)= ξ(p,v)
Funkcja
Y=f(x)=f [ξ (p,v)]=y (p,v)
Nazywa się funkcją podaży towaru
Funkcja podaży towaru przyjmuje wartości rzeczywiste nieujemne. Funkcja y(eta) ma takie same własności jak funkcja ξ
Reakcja przedsiębiorstwa na zmianę cen:
Pochodna
![]()
Opisuje reakcję optymalnej wielkości produkcji na zmianę ceny p wytwarzanego towaru
![]()
Wzrost ceny p wytwarzanego zawsze prowadzi do zwiększenia optymalnej wielkości produkcji.
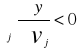
Wzrost ceny niektórych czynników produkcji (nakładów) powoduje spadek optymalnej wielkości produkcji
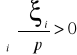
Wzrost ceny wytwarzanego towaru prowadzi do zwiększenia popytu na niektóre czynniki produkcji
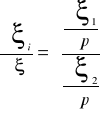
Optymalna wielkość nakładów na zmianę ceny p
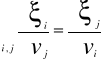
Wpływ zmiany ceny i-tego nakładu na popyt na j-ty nakład jest taki sam jak wpływ zmiany ceny j-tego nakładu na popyt na i-ty nakład
![]()
(Zależność między wektorami) Wzrost ceny produkowanego towaru powoduje wzrost popytu na i-ty czynnik produkcji, gdy zwiększenie ilości tego czynnika prowadzi do obniżenia optymalnego poziomu produkcji
Założenie
Gdy ceny są ustalone p i v a przedsiębiorstwo zdecydowało się na y-wielkość produkcji (jaką przedsięb. Otrzyma) to może ono być zainteresowane minimalizacją kosztów produkcji
Minimalizacja kosztów produkcji
Zadanie1
Wyznaczyć wektor nakładów x tak aby <v,x> min przy ograniczeniach .
F(x)=y x≥Θ
Można dowieść, że jeśli funkcja produkcji jest funkcją silnie wklęsłą to dla każdej wartości y>0 zadanie powyższe ma dokładnie jedno rozwiązanie x*
Funkcje: c:R1+R1+
Która przyporządkowuje poziomowi produkcji y>0 minimalny koszt otrzymanie takiej produkcji tj.
![]()
Y=f(x) x≥Θ
Nazywamy funkcją kosztów przedsiębiorstwa
Funkcja kosztów c jest:
A)ciągła
b)dodatnio jednorodna stopnia 1-ego
Znając funkcję kosztów c można wyznaczyć optymalną wielkość produkcji dla przedsiębiorstwa rozwiązując następujące zadanie.
![]()
Zadanie2
Wyznaczyć taką wielkość produkcji y , że: py-c(y)max
Przy ograniczeniu y≥0
Jeżeli funkcja kosztów c jest różniczkowalna to y*>0 jest optymalną wielkością produkcji ⇔gdy
p=cII (y*)
cII(y*)>0
Strategia krótkookresowa w przedsiębiorstwach
Omawiając strategię długookresową przyjmowaliśmy, że przedsięb może w każdej chwili wybrać i otrzymać dowolny wektor nakładów x≥Θ
W krótkich okresach czasu może tobyć niemożliwe np. niektóre z towarów zużywanych w procesie produkcji mogą być dostępne jedynie w ograniczonych ilościach
Zadanie3 (maksymalizacji zysku)
Wyznaczyć taki wektor nakładów x, że pf(x)-<v,x>max przy ograniczeniach y(x)= Θ (g(x)≤ Θ) x≥Θ
Przedsiębiorstwo w warunkach monopolu
Założenie
Przedsięb mające monopol na wytwarzany towar ma pływ na cenę p tego towaru, w tym wypadku p=p(y)
Przyjmujemy że .
PI(y)<0
Monopolista jest gotowy obniżyć cenę a zwiększyć sprzedaż
2. Pozostałe przedsięb działające na rynku mają wpływ na ceny vi (i=1,...k) tych nakładów
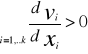
3.
⇓
v = v(x1,...xk)=(v1(x1),...,vk(xk))
⇓
Nasz producent jest skłonny zapłacić wyższą cenę za dodatkowe niezbędne mu nakłady
Zadanie4(maksymalizacji zysku)
Wyznaczyć taki wektor nakładów x aby p(y)=y-<v(x),x)max przy ograniczeniach y=f(x) x≥Θ
T: Statyczne modele równowagi. Prosty model wymiany.
Zał
Poniżej sformułujemy matematyczny model rynku, na którym wielu handlowców stara się zmaksymalizować swoją funkcję użyteczności w drodze wymiany towarów (bez udziału pieniędzy)
Na rynku znajduje się i jest dostępnych n doskonale podzielnych towarów
W wymianie bierze udział m handlowców
Każdy z handlowców posiada pewien koszyk towarów (koszyk początkowy-a k=(a1k, a2k,...a m k)≥0) k=1,...m j koszyk ten może być skonsumowany przez handlowca lub wymieniony na inny koszyk
Nie ma przymusu zawierania transakcji
Żadnemu z handlowców nie można zabronić dokonania korzystnej dla niego wymiany
Każdy z handlowców zachowuje się racjonalnie czyli godzi się na wymianę wtedy gdy nowy koszyk jest niegorszy od tego którego posiada
Każdy z handlowców posiada pełną informację na temat preferencji i początkowych zasobów koszyków wszystkich innych handlowców.
Gdyby:
![]()
Relacja słabej preferencji k-tego handlowca (k=1,...n)
![]()
Definicja
Alokacją dopuszczalną nazywamy każdy n°m wymiarowy wektor x=(x1, x2, ..., xm) spełniający warunek:
![]()
F(a)-zbiór wszystkich alokacji dopuszczalnych odpowiadających alokacji początkowej
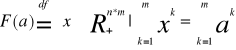
![]()
Każda alokacja dopuszczalna jest redystrybucją (wtórnym podziałem)koszyków początkowych.
Definicja
Alokację x∈F(a) nazywamy lokowaną przez koalicję S⊂{1,2,...,m} jeżeli isnieje alokacja y∈F(a) y=(y1, y2, ...y m) taka że:
suma po k∈S
![]()
2)
![]()
3)
![]()
Przykład
Alokacja
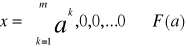
W której wszystkie koszyki należą do pierwszego handlowca jest blokowana przez koalicję utworzoną z S={2,3,...,m} pozostałych handlowców y∈F(a) y=a=(a1, a2,...,a k)
Wykład8
Alokacje, które mogą być blokowane przez jakąś koalicję nie mają szans na dowolną realizację. Zrealizowane mogą być tylko takie alokacje, które nie mogą być blokowane przez żadną koalicję- alokacje nieblokowane.
Definicja
Alokację x∈F(a) nazywamy optymalną w sensie Pareto (Pareto-optymalną) jeżeli nie istnieje alokacja x∈F(a) taka, że:
![]()
![]()
(k=1,2,...m)
Interpretacja:
Alokacja x=(x1,...xm) ∈F(a) jest zatem optymalna w sensie Pareto jeżeli nie istnieje alokacja y=(y I,...ym) ∈F(a), która dla każdego z handlowców jest nie gorsza od x a przynajmniej dla jednego jest lepsza od x.
Zbiór wszystkich alokacji Pareto- optymalnych P(a)
Można dowieść, że dla każdej alokacji początkowej a=(a1,....a m) zachodzą następujące inkluzje
C(a)⊂P(a)⊂F(a)
T:Prostokąt Edgewortha (PE) (Edgeworth's box)
Załóżmy że na rynku wymienia towary dwóch handlowców (m=2) liczba towarów też równa jest 2 (n=2)
A11+a12
A12 02
2-gi towar
a21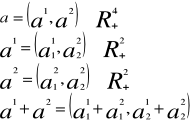
01 1-szy towar a11
Przyjmijmy że krzywe obojętności każdego z handlowców są silnie wypukłe
01
01
Przez każdy punkt PE przechodzi dokładnie jedna krzywa obojętności każdego z handlowców
Zbiór punktów PE(zbiór alokacji dopuszczalnych) w których krzywe obojętności pierwszego handlowca są styczne do krzywych obojętności drugiego handlowca nazywamy krzywą kontraktów (krzywa kontraktowa) Krzywa kontraktów jest zbiorem alokacji optymalnych w sensie Pareto.
Krzywe obojętności przechodzące przez punkt a (alok. Początkowa) dzielą PE na dwie części. Obszar na zewnątrz widocznej na rys.”soczewki” i obszar złożony z punktów tej „soczewki” (razem z brzegiem). Każda alokacja położona na zewnątrz „soczewki” (nawet alok. Optymalna w sensie Pareto) będzie zawsze blokowana przez jednego z handlowców.
Zbiór wszystkich alokacji, które nie są blokowane (czyli jądro wymiany C(a)) jest częścią wspólną „soczewki” oraz krzywej kontraktów P(a)
T: Model równowagi rynkowej Arrowa-Hurwicza
Model opisuje zachowanie się grupy handlowców (m handlowców) którzy przybywają z towarami na rynek, aby je sprzedać i za uzyskane w ten sposób pieniądze kupić inne potrzebne im towary.
Zakładamy, że ceny towarów są jednolite na całym rynku.
Problem:
Czy można tak ustalić ceny towarów na rynku aby:
1) Każdy z handlowców mógł kupić koszyk towarów, który maksymalizuje jego funkcję użyteczności (w ramach budżetu tylko uzyskanego ze sprzedaży koszyka)
popyt na towary był równy ich podaży
m handlowców
n towarów
![]()
-koszyk początkowy k-tego handlowca
![]()
-koszyk towarów, który k-ty handlowiec chciałby nabyć
p=(p1, p2,....,p n) ≥Θ
wektor cen
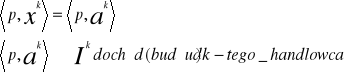
![]()
Wybierając koszyki handlowcy kierują się indywidualnymi preferencjami odzwierciedlanymi przez funkcje użyteczności:
![]()
Założenie:
Każdy handlowiec zna wszystkie pary (a k, u k) k=1,...,m
Zadanie1
Uk(x)max
Przy ograniczeniach <p,x>=Ik x≥Θ
Z poznanych twierdzeń wynika że jeśli każda z funkcji użyteczności u k jest silnie wklęsła, rosnąca i dwukrotnie różniczkowalna to optymalny koszyk dla tego handlowca czyli koszyk xk jest ciągła funkcją wektora cen p oraz budżetu Ik
![]()
ϕk -funkcja popytu k-tego handlowca (konsumenta)
Ponieważ
Ik=<p, ak>
Gdzie a k∈Rn+ jest ustalone
Definicja
Wektorem nadmiernego popytu na towary nazywamy wektor
![]()
Ponieważ
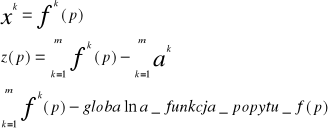
Interpretacja:
Z(p)= (z1(p), z2(p),...zn(p))∈Rn
Wtedy z i (p)>0- nadwyżka popytu nad podażą i-tego towaru
Kiedy z i (p)<0-nadmierna podaż i-tego towaru (przy cenach p=(p1,...p n)
Kiedy z i (p)=0 na rynku jest równowaga cząstkowa
Definicje
Mówimy że rynek jest w równowadze gdy ustaliły się na nim ceny
![]()
Przy których
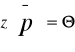
Wektor cen p (z daszkiem) spełniający powyższy warunek nazywamy wektorem cen równowagi walrasowskiej (ogólnej)
Definicja równowagi walrasowskiej nazywa się wektor
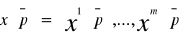
Utworzony z optymalnych koszyków wszystkich handlowców
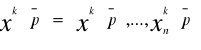
Zakupionych po cenach równowagi
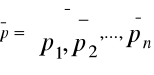
W(a) zbiór wszystkich alokacji równowagi walrasowskiej
Twierdzenie
Dla przyjętych założeń o funkcjach użyteczności uk oraz dla dowolnej alokacji początkowej a zachodzą inkluzje W(a)⊂C(a) ⊂P(a) [⊂F(a)]
Twierdzenie
Założenie
1)Funkcje popytu f k (k=1,...m) są różniczkowalne w zbiorze Rn+\{Θ}
![]()
2)
3)dla każdego wektora p należącego do zbioru:
![]()
oraz każdego wektora
![]()
gdzie
![]()
macierz Jacobiego funkcji
z(p)=(z(p),...zn(p))
spełnia warunek λ I(p) λT<0
Teza:
W modelu równowagi rynkowej Arrowa-Hurwicza istnieje dokładnie jeden wektor cen równowagi
![]()
Określony z dokładnością do mnożenia przez stałą
Macierz Jacobiego
Z(p)= (z1(p),..., z n(p))
Jest to macierz
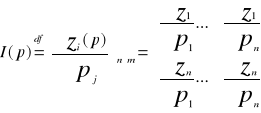
Wyznacznik Jacobiego I(p) nazywa się jakobianem funkcji z w punkcie p.
Wykład9
Temat: Równania różniczkowe zwyczajne
Pod koniec XVIIw powstała teoria równań różniczkowych. Izaak Newton, G.W. Leibniz
Definicja
Równanie różniczkowe zwyczajne jest to równanie w którym występują pochodne yI,yII, ...y (n) pewnej nieznanej funkcji y=y(t)
t- zmienna niezależna
y- zmienna zależna
W równaniu różniczkowym może też wystąpić szukana funkcja y=y(t) oraz zmienna niezależna t
Założenie
F(t, y, yI, yII,... y(n) )=0 (1)
F:Rn+1 R (n≥1)
F- jest ciągła w otwartym zbiorze U⊂Rn+2
Najczęściej t∈(-∞,∞) lub t∈<0, ∞)
Istnieją jeszcze równania cząstkowe, w których poszukiwana funkcja jest funkcją wielu zmiennych.
Równanie (1) jest równaniem różniczkowym n-tego rzędu, bo występują w niej pochodna szukanej funkcji y(n)
Y (n) =f(t, y, y I,... y(n-1) ) (2)
Przykład 1
Y I =a (a∈R)
Równanie różniczkowe rzędu pierwszego, normalne
Y(t)=at+c c∈R
Przykład 2
TyI +y II -et y2 =0 t∈(-∞,∞)
Równanie nieliniowe
Y II= ety2-tyI
Przykład 3
Załóżmy że są dane funkcja popytu i podaży na dane dobro
D=D(p) funkcja popytu
S=S(p) funkcja podaży p=p(t)
Jeżeli przyjmiemy że prędkość zmian cen jest proporcjonalna do nadmiernego popytu na rozpatrywany towar
![]()
E(p)- nadmierny popyt
To otrzymamy równanie różniczkowe
![]()
Równanie różniczkowe zwyczajne można podzielić na dwie obszerne klasy:
Liniowe
Nieliniowe
Definicja
Równanie n-tego rzędu nazywamy liniowym, jeżeli daje się przedstawić w postaci:
![]()
Których współczynniki a0, a1 , ...,an , g są samymi funkcjami zmiennej niezależnej t∈I
Uwagi
1) Jeśli współczynniki a0, a1, ...an nie zależą od zmiennej t to równanie liniowe jest o stałych współczynnikach
Gdy funkcja g jest identycznie równa 0 dla t∈I to równanie (3) nazywamy równaniem jednorodnym a jeżeli nie jest identyczne to nazywamy równaniem niejednorodnym
Przykład 4
5yIII + (sint)yII- et y=0 równanie liniowe III rzędu jednorodne
Definicja
Rozwiązaniem równania różniczkowego (1) nazywamy każdą funkcję y=y(t) posiadającą dla t∈I pochodne aż do n-tego rzędu włącznie i taką że
![]()
Wykres każdej funkcji y=y(t) będącej rozwiązaniem równania (1) nazywamy krzywą całkową tego równania
Przykład5
Łatwo sprawdzić, że każda funkcja postaci
![]()
C1, c2 ∈R
Jest tzw. Rozwiązaniem ogólnym równanie różniczkowego yII +yI+1,25y=2,5
Przyjmując np.
C1=-0,5 c2=1,55
Otrzymujemy jedną z nieskończenie wielu tzw. Rozwiązań szczególnych powyższego równania różniczkowego
![]()
2
T: Interpretacja geometryczne rozw. Równania różniczkowego. Pole kierunków
Y I= f(t,y) (*)
Niech y=y(t) jest rozwiązaniem równania (*) dla t∈I
Fakt że funkcja y jest rozwiązaniem rów (*) oznacza, że przy zadanym prostokątnym układzie współrzędnych styczną do krzywej całkowej y=y(t) ma w każdym leżącym na tej krzywej punkcie P(t,y) współczynnik kierunkowy k=f(t,y)
A zatem rozwiązanie równania różniczkowego (*) sprowadza się do następującego zadania.
Wiedząc, że każdemu punktowi o współrzędnych (f,y) z pewnego obszaru jest przyporządkowany pewien kierunek K=f(t,y) (kiedy zadanie jest tzw. Pole kierunków) Trzeba znaleźć wszystkie krzywe, które w każdym swoim punkcie P mają styczną o współczynniku kier. Wyznaczonym przez powyższe pole kierunków
Przykład 6
YI=y2 równanie rzędu pierwszego nieliniowe autonomiczne
Y2 ⇒f(t,y)
K=f(t,y)=y 2
Rozwiązaniem ogólnym jest funkcja
![]()
Rozwiązanie osobliwe y(t)=0
Rozwiązanie ogólne i szczególne równań różniczkowych
Rozwiązanie osobliwe
Def.
Rozwiązanie równania różniczkowego-tego rzędu nazywamy rozw. Ogólnym jeżeli w rozw. Tym wyst n różnych stalych
Y=y(t, c1,... c n) c1...c n∈R
Każde rozwiązanie które otrzymuje się z rozw. Ogólnego wstawiając za wspomniane stałe ustalone wartości liczbowe nazywamy rozw. Szczególnym równanie różniczkowego
Rozw rów różniczkowego które nie może być otrzymane z rów ogólnego w wyżej opisany sposób nazywamy rozw. Osobliwym
Równanie roż może (ale nie musi) posiadać rozw. Osobliwego
Przykład7
Y II +y=0 (*)
Y(t)=c1 cost +c2 sint (c1, c2∈R)
Rozw nie posiada rozw różniczkowego
Przykład8
(y I)3-y=0
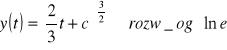
y(t)≡0 rozw osobliwe
T: Warunki początkowe i brzegowe . Problem Cauchiego
Chcąc wyznaczyć stała c1,...cn wyst w rozw ogólnym rów n-tego rzędu musimy narzucić na rozw ogólne pewne warunki. Liczba tych warunków musi być równa rzędowi równania n
Warunki odnoszące się do jednegoo punktu t0∈I nazywamy warunkami początkowymi. Warunki odnoszące się do więcej niż jednego punktu I nazywamy warunkami brzegowymi.
Przykład9
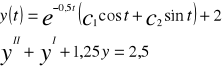
Problem Cauchiego
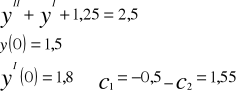
![]()
Równanie różniczkowe wraz z narzuconymi warunkami początkowymi tworzą tzw. Problem Cauchiego
Przykład10(przykład problemu brzegowego)
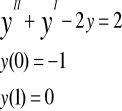
Rozwiązanie
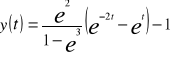
Problem Cauchiego
Znaleźć rozw y=y(t) równania róż
![]()
Spełniające warunki początkowe
![]()
Twierdzenie (o istnieniu jednoznaczności rozw problemu Cauchiego)
Jeżeli wyst w rów (*) funkcja f traktowana jako funkcja n+1 zmiennych t, y, yI...yn-1
Jest ciągłą i ma ograniczone pochodne cząstkowe
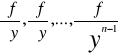
W pewnym obszarze D⊂R n+1 zawierającym punkt (t 0, y0, t10,..y n-10) to istnieje przedział (a,b) oraz określana dla t∈(a,b) dokładnie jedna n-krotnie różniczkowalna w sposób ciągły funkcja y=y(t) spełniająca równanie (*) i warunki początkowe tego równania
Wykład 10
T: Równania różniczkowe pierwszego rzędu
Równania o zmiennych rozdzielonych
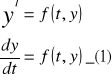
Jeżeli funkcję f daje się przedstawić w postaci ilorazu
![]()
To daje się przedstawić w postaci
![]()
Można je także zapisać w postaci:
P(t,y)dt+Q(t,y)dy=0 (2) postać różniczkowa
Definicja
Równanie różniczkowe I-ego rzędu nazywamy równaniem o zmiennych rozdzielonych jeżeli ma poniższą postać różniczkową P(t)dt+Q(y)dy=0 (3)
UWAGA
Równanie postaci
M(t)N(y)dt+P(t)Q(y)dy=0 (4) równanie o zmiennych separowanych
Można łatwo sprowadzić do postaci (3) dzieląc je stronami przez iloczyn N(y)P(t)
![]()
Aby znaleźć rozwiązanie ogólne równania (3) wystarczy scałkować to równanie stronami
![]()
Równanie (5) daje uwikłany związek między zmiennymi y i t, czyli związek postaci
φ(t,y,c)=0 (6)
Równanie (6) jest to całka ogólna równanie (3)
Jeżeli potrafimy z równania (6) wyznaczyć y jako funkcje zmiennej niezależnej t, to otrzymujemy rozwiązanie ogólne równania (3)
Y=y(t, c1)
Przykład1
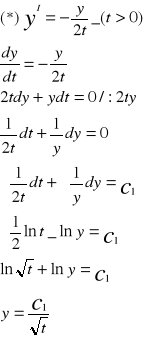
Rozw ogólne równania (*)
Równanie (*) ma też rozwiązanie osobliwe y(t)≡0
Wiele równań różniczkowych I-rzędu daje się za pomocą różnego rodzaju przedstawień, przekształceń sprowadzić do równania o zmiennych rozdzielonych np. równanie jednorodne i Bernoulliego
Jednorodne
YI=f(t,y) w których funkcja f jest funkcja jednorodną
![]()
Przykład2
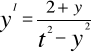
Bernoulliego
YI + P(t)y=Q(t)yn
Np.
YI-ty= -ty3
Liniowe równanie różniczkowe I-go rzędu
A1 (t)y I+ a0 (t) y=y(t) (7)
Jeśli dla t∈I a1(t)≠0
To równanie (7) przedstwić można w postaci
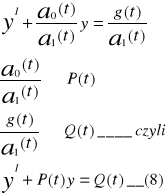
Rozwiązanie
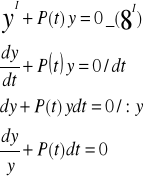
Całkując stronami otrzymamy rozwiązanie ogólne równania jednorodnego (8I)
![]()
c∈R (9)
Rozwiązanie ogólne równania niejednorodnego (8) otrzymujemy stosując tzw. Metodę uzmienniania stałych
Poszukujemy rozwiązywania równania (8) wstając do niego funkcję
![]()
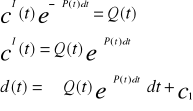
Otrzymujemy
![]()
Podstawiając powyższą funkcję do wzoru (9) otrzymujemy wzór na rozwiązanie ogólne niejednorodnego równania różniczkowego postaci I-go rzędu postaci (8)
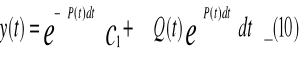
Ze wzoru (10) widać, że rozwiązanie ogólne równanie (8) jest sumą:
-rozwiązania ogólnego równania jednorodnego (8I)
-rozwiązania szczególnego równania równoważnego niejednorodnego (8) (po wstawieniu c1=0)
Liniowe równania różniczkowe wyższych rzędów
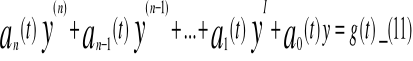
Uproszczenieoperator-funkcjom przyporządkowuje funkcje
![]()
Postać operatora
L[y]=y(t) (11I)
Twierdzenie
Jeżeli funkcje y1=y1(t),...y n=y n(t) są rozwiązaniem równania jednorodnego
L[y]=0 (12)
To każda ich kombinacja liniowa
![]()
Też jest rozwiązaniem tego równania
Definicja
Funkcje y1,...,yn nazywamy liniowo niezależnymi w przedziale I jeżeli
![]()
Przykład3
{1,t,t2} liniowo niezależne w I=(-∞,∞)
{1,t,0} nie są liniowo niezależne w I=(-∞,∞)
Wrońskian od J.M.Hoene-Wroński 1776-1853
Zał
Y1, y2,...yn funkcje n-1 krotnie różniczkowalne w I
Definicja
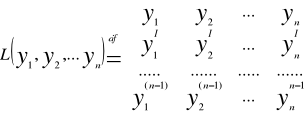
Twierdzenie
Niech funkcje y1=y1(t),...,yn =yn(t) (t∈I) będą rozwiązaniami równania
L[y]=0
Wkw ma to by funkcje te były liniowo niezależne w przedziale I jest aby istniał punkt t0∈I taki że W(y1, y2,...,yn) ≠0
Twierdzenie
Jeżeli y1=y1(t),...,yn =yn(t) są liniowo niezależnymi rozwiązaniami równania L[y]=0 dla t∈I oraz c1,...c n są dowolnymi stałymi to funkcje
![]()
Jest rozwiązaniem tego równania
Twierdzenie
Jeżeli funkcja
![]()
Jest rozwiązaniem ogólnym równania jednorodnego L[y]=0 oraz funkcja
![]()
Jest jakimkolwiek rozwiązaniem szczególnym równania niejednorodnego L[y]=g(t) to funkcja
![]()
Jest rozwiązaniem ogólnym równania niejednorodnego
Rozwiązywanie równań
I Tworzymy![]()
tzw. Równanie charakterystyczne dla równania (*)
![]()
II Rozwiązujemy równanie(**)
Równanie charakterystyczne może mieć wyłącznie pierwiastki rzeczywiste
-różne
-wielokrotne
Równanie może mieć pierwiastki i rzeczywiste i zespolone
-jednorodne
-wielokrotne
Przykład4
1)Niech r1, r2, ...r n będą rzeczywistymi i różnymi pierwiastkami charakterystycznego równania (**)
Rozwiązanie ogólne równania (*) ma wtedy postać:
![]()
Np.
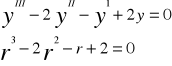
Pierwiastki
R1= -1 r2= 1 r3=2
Wykład11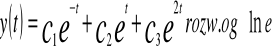
I Pierwiastki rzeczywiste wielokrotne
Twierdzenie
Jeżeli r jest k-krotnym (k≥1) pierwiastki równania charakterystycznego dla równania różniczkowego L[y]=0 to funkcja postaci: er t, ter t, ...t k-1er t są liniowo niezależnymi rozw równania różniczkowego L[y]=0
Przykład1
Y(7) +y(6) -6y(5) -6y(4) +9yIII +9yIII -4yI - 4y=0
Y(7) +y(6) -6y(5) -6y(4) +9yIII +9yIII -4yI - 4yL[y]
R7 +r6 +6r5 -6r4 +9r2 -4r -4 =0
R1= -2 R2= 2 r3=r4=r5= -1 r6=r7=1
Y1(t)=e -2t y6(t)=e t
Y2(t)= e 2t y7(t)=te t
Y3(t)=e -t
Y4(t)= t e -t
Y5(t)=t2 e -t
Rozwiązanie ogólne:
Y(t)=c1y1(t)+...+c7y7(t)=c1e -2t+...+c7tet
II Pierwiastki zespolone różne
Twierdzenie
Jeżeli równanie charakterystyczne (rów kwadratowe) ma dwa różne pierwiastki zespolone
R1= a +bi ∧ r2=a-bi
To rozw ogólne L[y]=0 ma postać
![]()
Przykład2
YIII - 3yII +9yI +13y=0
R3-3r2+9r+13=0
R1= -1 y1(t)= e -t
R2=2 +3i y2(t)=e2tcos 3t
R3=2-3i y3(t)=e2tsin3t
Rozwiązanie ogólne:
![]()
III Wielokrotne pierwiastki zespolone
Przypuśćmy, że liczby r=a±bc są k-krotnymi zespolonymi pierwiastkami dla równanie L[y]=0. Pierwiastkom tym (a jest ich 2k)odpowiada 2k liniowo niezależnych rozwiązań równania L[y}=0 Rozwiązania te mają postać
Y1(t)=ea t cosbt y2(t)=ea t sinbt
Y3(t)=tea t cosbt y4(t)=tea t sinbt
Y5(t)=t2ea t cosbt y6(t)=t2ea t sinbt
............................. ............................
y2k-1(t)=tk-1 ea t cosbt y2k(t)=t k-1 ea t sinbt
Przykład3
Y(6) - 5y(5) +32yIII- 84yII+ 92yI -48y=0
R6-5r5+32r3-84r2+92r-48=0
R1= -3 y1(t)=e -3t
R2=4 y2(t)=e 4t
R3=r4=1-i y3(t)=et sint ∧ y4(t)=tet sint
R5=r6=1+i y5(t)=et cost ∧ y6(t)=tet cost
Ogólne rozwiązanie
![]()
IV Rozwiązanie ogólne równania L[y]=g(t) (*)
Twierdzenie
Jeżeli funkcje y1=y1(t),...y n= yn(t) są liniowo niezależnymi rozwiązaniami L[y]=0 to rozwiązanie szczególne równania
![]()
Ma postać
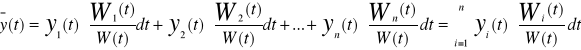
Gdzie W(t) jest wrońskianem funkcji y1....y n natomiast
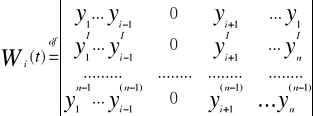
Przykład4
Y III- y II - y I +y= e t (*)
Ogólnym rozwiązaniem równania jednorodnego jest funkcja
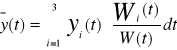
![]()
YIII- y II- yI +y= et
Ogólnym rozwiązaniem równania jednorodnego jest funkcja
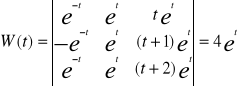
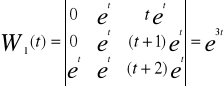
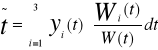
![]()
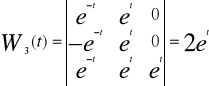
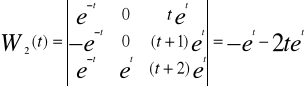
Po scałkowaniu i pominięciu stałej całkowej
Rozwiązanie szczególne
![]()
Odp:
Więc szczególne rozwiązanie równania różniczkowego (*) ma postać
![]()
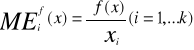
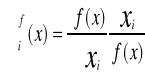
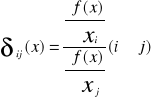
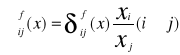
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
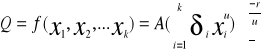
![]()
![]()
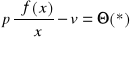
![]()
![]()
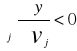
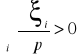
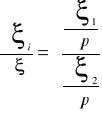
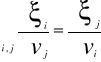
![]()
![]()
![]()
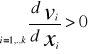
![]()
![]()
![]()
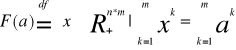
![]()
![]()
![]()
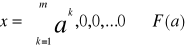
![]()
![]()
A(a1,a2)
X=(x1,x2)
A12
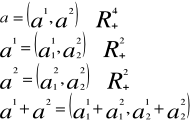
A2 2
Wzrost użyt
Wzrost użyt
a
C(a)
![]()
![]()
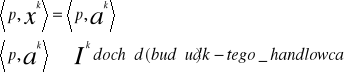
![]()
![]()
![]()
![]()
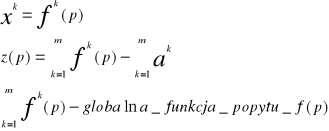
![]()
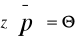
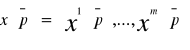
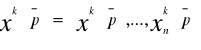
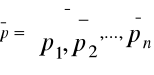
![]()
![]()
![]()
![]()
![]()
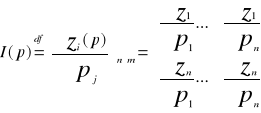
![]()
![]()
![]()
![]()
![]()
![]()
![]()
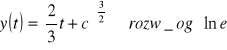
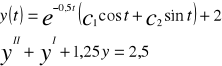
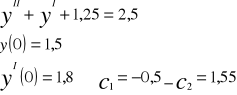
![]()
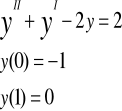
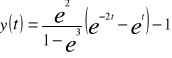
![]()
![]()
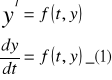
![]()
![]()
![]()
![]()
![]()
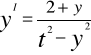
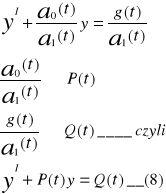
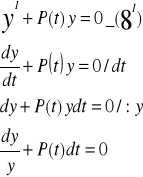
![]()
![]()
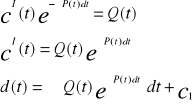
![]()
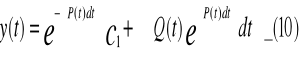
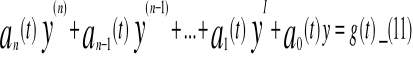
![]()
![]()
![]()
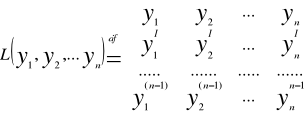
![]()
![]()
![]()
![]()
![]()
![]()
![]()
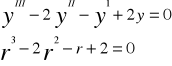
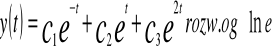
![]()
![]()
![]()
![]()
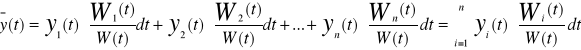
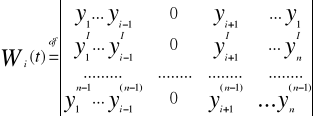
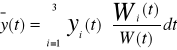
![]()
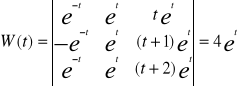
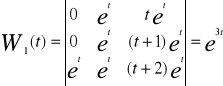
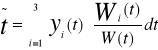
![]()
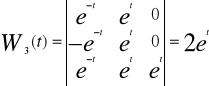
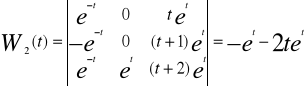
![]()
![]()
Wyszukiwarka