cz1.
WSZYSTKIE TEKSTY SA TAKEI SAME JAK W KAZDEJ INNEJ PRACY - TAKZ E JEŚLI PRZEPISZESZ TO ZYWCEM TO JEST 100% PRAWDOPODOBNE ZE ZACZNIE CIE PYTAC O WSZYSTKO JAK I SKAD OBLICZYLES. Staraj się żeby praca nie była podobna, zmieniaj tekst, zdania, rysunki, układ strony, ale generalnei warto cos wiedzcie jak jest to policzone bo Ci ludzie zawsze i każdego potrafią zapytac ukradkiem o jakas głupotę, im mniej człowiek wie tym go bardziej pytaja.
Zadanie 1 - wyprowadzenie równań równowagi płynu.
Rozważamy dowolną przestrzeń ![]()
wypełnioną płynem idealnym
![]()
![]()
![]()
![]()
![]()
![]()
![]()
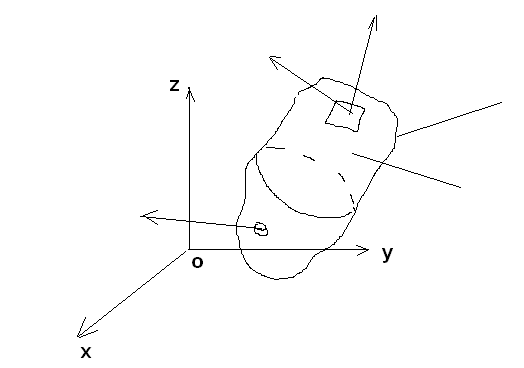
- wnętrze obszaru
![]()
![]()
- powierzchnia ograniczająca obszar
ds - elementarny wycinek powierzchni dV - elementarny wycinek wnętrza obszaru
ΔFp - jednostkowa siła powierzchniowa
![]()
ΔFv - jednostkowa siła objętościowa
![]()
- wektor normalny do wycinka ds.
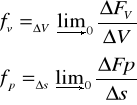
- gęstość sił objętościowych
- gęstość sił powierzchniowych
Siły powierzchniowe zależą od usytuowania rozpatrywanej powierzchni, nie są zatem wielkością stałą i niezależną. Niezależnie od doboru powierzchni opisywał będzie stan cieczy tensor napręzeń- charakteryzujący naprężenia w danym punkcie. Na jego wartości nie ma wpływu sposób doboru powierzchni.
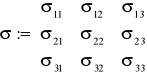
- tensor naprężeń
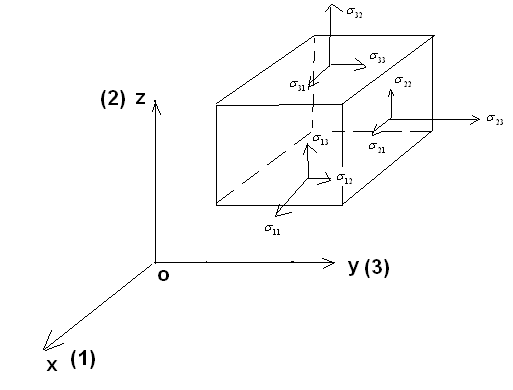
Ze względu na równości odpowiednich naprężeń stycznych, macierz ta jest macierzą symetryczną, czyli: ![]()
, ponieważ ![]()
.
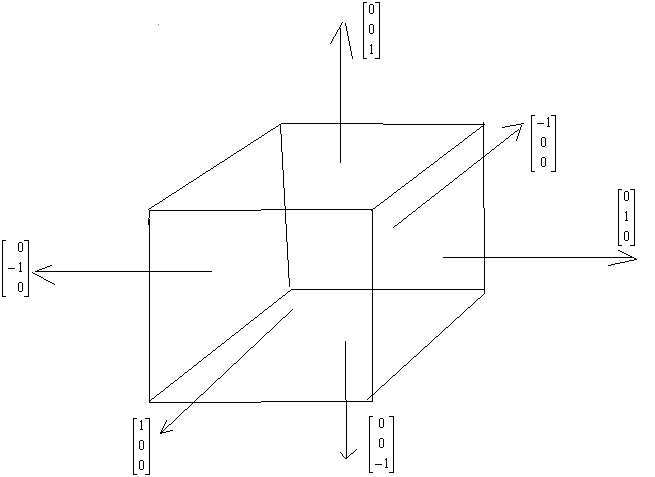
![]()
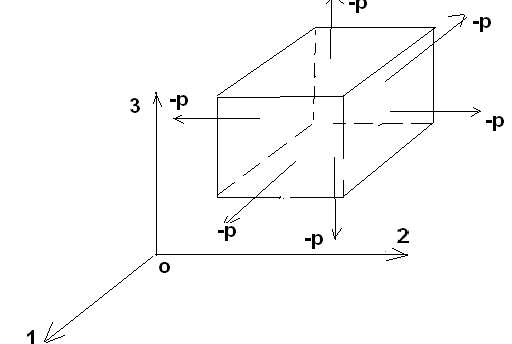
Rysunki przedstawiają elementarny wycinek obszaru Ω- czyli d Ω, oraz jego naprężenia i współrzędne wektora
![]()
Są to makroskopowe ujęcia punktu obszaru. Można spostrzec ze na jego powierzchnię działają siły powierzchniowe zależne od doboru powierzchni. Ściana powierzchni opisywana jest przez wektor
Ogólny stan naprężenia w danym punkcie przedstawia tensor naprężeń σ Siła powierzchniowa będzie zatem równa:
![]()
- jest to wektor [N/m] = [Pa]
(R3) (R3x3) (R3)
Znalezienie siły wypadkowej wymaga scałkowania po powierzchni:
![]()
; [N]
Analizując budowę tensora σ zauważymy, że:
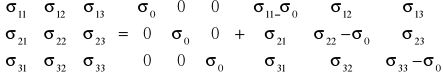
Tensor σ tensor kulisty tensor dewiatorowi - σD
Gdzie: ![]()
; oraz ![]()
- ślad macierzy σ
Tensor kulisty to 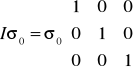
Czyli ostatecznie: ![]()
Tensor kulisty odpowiedzialny jest za opis matematyczny wszechstronnego ściskania/rozciągania. Dewiator jest wyrażeniem związanym ze zmianą postaci ciala - ścinaniem. Ponieważ przy rozpatrywaniu płynu nie możemy mowić o rozciąganiu, a σ0 ma kierunek naprężeń rozciągających, to ma on zawsze wartość ujemna. Wartość tę nazywamy ciśnieniem.
![]()
; ![]()
; ![]()
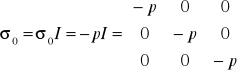
Po uwzględnieniu założenia, że siła powierzchniowa w każdym kierunku jest jednakowa i skierowana prostopadle do powierzchni, to dla danej chwili:
![]()
Jest to całka wektoru
Rozważając kolejno siły objętościowe:
![]()
[N/m3] - gęstość siły objętościowej.
Są to siły wewnętrzne, wzajemne. Obliczamy ich wypadkową dla danej chwili:
![]()
Siła wypadkowa w całym obszarze to ![]()
:
![]()
Na mocy Twierdzenia Gaussa-Ostrogradskij-ego możemy zastąpić całkę powierzchniową całka objętosciową w poniższy sposób:
![]()
Aby zachowana była równowaga to: ![]()
dla każdego obszaru Ω czyli:
![]()
![]()
Musi tak być dla każdego obszaru Ω 0 (ponieważ równie dobrze wymagać można zachowania równowagi i tego obszaru). Zależność ![]()
= 0 nazywamy równaniem równowagi ośrodka ciągłego, lub równaniem Eulera. Obowiązuje ono dla płynu nielepkiego.
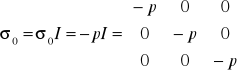
, a wtedy: 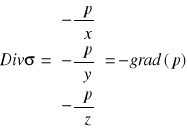
Możemy zatem napisać równanie równowagi dla płynu:
Ponieważ:![]()
, oraz ![]()
to ostatecznie:
![]()
Dla zachowania pełnej równowagi spełnione musi być też równanie momentów.
![]()
Po przekształceniach analogicznych do tych z warunku na równowagę sił, możemy zauważyć że jeżeli siłą wypadkowa będzie równa zeru, to niezależnie od tego na jakim ramieniu będzie działała, również da moment równy zeru. A zatem warunkiem wystarczającym do spełnienia aby ośrodek był w równowadze, jest zależność:
![]()
![]()
Jest to warunek równowagi płynu doskonałego.
Zadanie 2 - cysterna
![]()
α%= |
13 |
% |
|
α= |
7,4 |
° |
L= |
7,6 |
[m] |
|
|
|
|
D= |
2,1 |
[m] |
|
|
|
|
d= |
1 |
[m] |
|
|
|
|
ρcieczy= |
1000 |
[kg/m3] |
|
|
|
|
a= |
0,28 |
g |
|
Współrzędne klapy: |
|
|
g= |
9,81 |
[ms2] |
|
Xk= |
7,6 |
klapa tylna |
Pa= |
101325 |
[Pa] |
|
Yk= |
1,05 |
|
Znajduję siły objętościowe działające na ciecz w poruszającej się cysternie:
Siła ciężkości: fg =ρ g - skierowana zgodnie z kierunkiem wektora grawitacji
Sila bezwładności fb = - ρa skierowane zawsze przeciwnie do przyspieszenia cysterny - czyli zgodnie z kierunkiem osi x
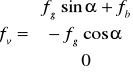
[N/m3]- jest to wektor wypadkowy sił objętościowych w układzie (x,y,z), obliczam jego współrzędne:
fx= |
4011 |
fy= |
-9728 |
fz= |
0 |
Mając współrzędne możemy usytuować wektor wypadkowy w płaszczyźnie cysterny. Wektor wskazuje kierunek najszybszego wzrostu cisnienia, po przeciwnej stronie jest kierunek spadku. W rogu, wskazywanym przez kierunek spadku ciśnienia znajduje się pęcherzyk powietrza, panuje w nim ciśnienie atmosferyczne.
Linie prostopadłe do wektora wypadkowego to izobary - linie stałego ciśnienia.
Wiemy, że: ![]()
- równanie równowagi dla płynu
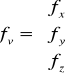
natomiast 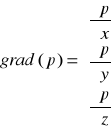
czyli z tego wynika, że: ![]()
A zatem możemy napisać korzystając z różniczki zupełnej:
![]()
ale ponieważ ![]()
to w każdym otoczeniu punktow o współrzędnych x,y,z pochodne cząstkowe są stałe i możemy zastąpić: ![]()
, ![]()
![]()
i napisać równanie ciśnień w postaci:
![]()
I wtedy: p(x,y,z) =
p(x,y,z) = |
4011 |
x + |
-9728 |
y + |
0 |
z + c |
C - obliczamy z warunku brzegowego na ciśnienie atmosferyczne w punkcie gdzie znajduje się pęcherzyk powietrza.
Współrzędne punktu pęcherzyka to:
Xp= |
0 |
Yp= |
2,1 |
Czyli p( xp, yp) = 101325 =4011 xp - 9728 yp + c
Po obliczeniu:
c= |
121754 |
[Pa] |
Równanie ciśnienia ma następującą postać:
p(x,y,z) = |
4011 |
x + |
-9728 |
y + |
121754 |
Aby znaleźć siłę naporu wody na klapę należy obliczyć ciśnienie w punkcie środka ciężkości tej klapy, a następnie pomnożyć je przez pole powierzchni tej klapy:
Współrzędne klapy: |
|
|
|
|
|
Xk= |
7,6 |
klapa tylna |
p(xk, yk)= |
142027 |
[Pa] |
Yk= |
1,05 |
|
|
|
|
Aklapy=πd2/4= |
0,79 |
[m2] |
|
|
|
F=A*p(xk, yk)= |
110781 |
[N] |
-odpowiedź |
||
Zadanie 2 - pława
H0= |
1,4 |
[m] |
m0= |
205 |
[kg] |
δ= |
0,003 |
[m] |
ρstali= |
7400 |
[kg/m3] |
ρwody= |
1000 |
[kg/m3] |
g= |
9,81 |
[m/s2] |
Najpierw obliczam objętość zanurzoną, masę i siłę wyporu pontonu, i zestawu pontonów:
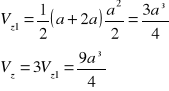

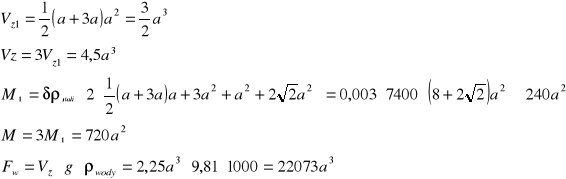
Równanie równowagi układu:
![]()
22073 |
a3 |
= |
7063 |
a2+ |
2011 |
|
22073 |
a3 |
- |
7063 |
a2 - |
2011 |
=0 |
Za pomocą Excela obliczam wartości dla kolejnych wartości parametru a i znajduję pierwsze dodatnie rozwiązanie. Wartość dokładna rozwiązania to 0,589 m, przyjmuję do dalszych obliczeń wartość a = 0,6 [m]
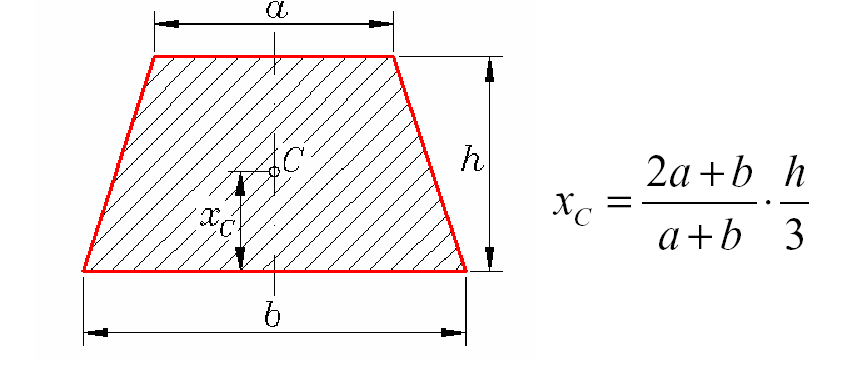
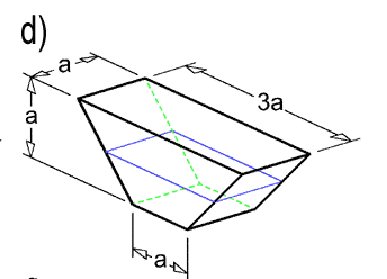
Następnie trzeba obliczyc polozenie środka ciężkości pontonów, zestawu pontonów i pławy oraz srodka wyporu. Pontony nie są symetryczne względem płaszczyzny poziomej. Polozenie srodka ciężkości ściany pontonu w kształcie trapezu obliczam wedlug schematu:
Srodek ciężkości jest zlozeniem srodkow ciężkości wszystkich ścian pontonu:
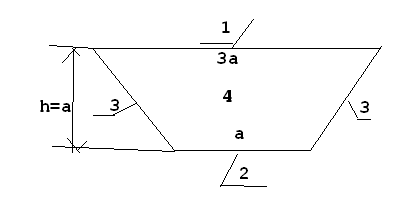
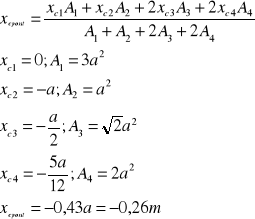
xc pont= |
-0,26 |
[m] |
M= |
259 |
[kg] |
xc plawy=Ho= |
1,4 |
[m] |
m0= |
205 |
[kg] |
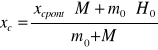
xc= |
0,47 |
[m] |
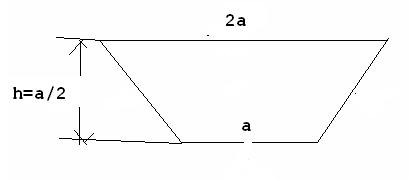
Środek wyporu pontonu obliczam jako środek ciężkości objętości zanurzonej pontonu, przy czym zgodnie z zalozeniem ponton przyjmuję zanurzony do polowy swojej wysokości.
![]()
Odległość pomiędzy środkiem wyporu i środkiem ciężkości:
lm=|xcxw|= |
0,8 |
[m] |
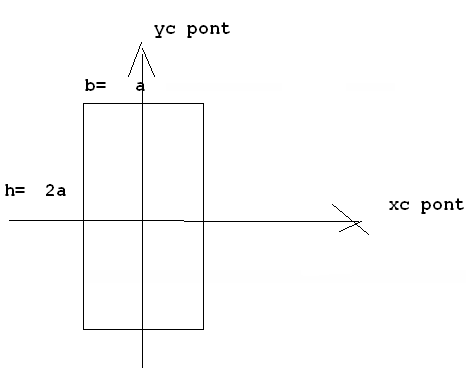
Obliczam momenty bezwładności przekroju względem jego głównych centralnych osi bezwładności. Przekrój zanurzeniowy pontonu jest prostokątem o bokach a i 2a
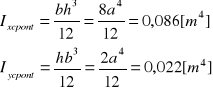
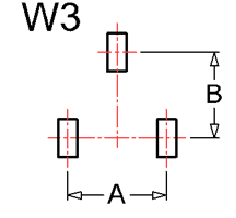
Obliczam momenty bezwładności układu pontonów względem głownej centralnej osi bezwładności Przyjmuję promień rozstawu pław A=4m, B=3m
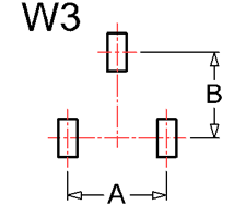
Pionowa glowna centralna oś bezwladnosci jest osią symetrii
Poziomą znaduję w następujący sposób:
(Xc jest współrzędna położenia osi centralnej licząc
od punktu przecięcia się zaznaczonych oci charakterystycznych.
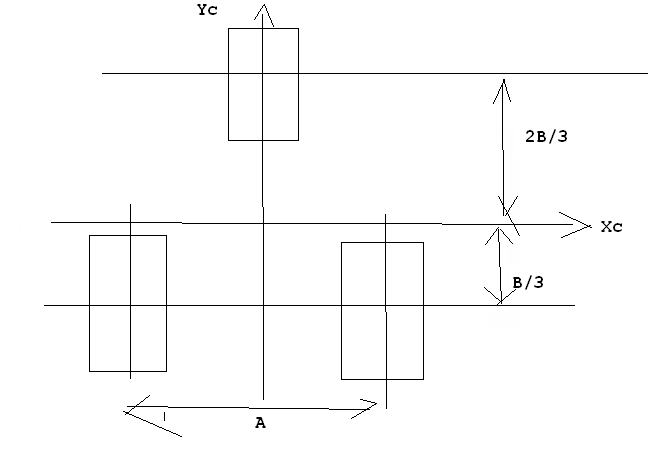
![]()
Osiami wywrotu będą osie glowne centralne.
Obliczam oba momenty bezwładności-względem
obu osi żeby wiedziec względem której pława
jest mniej stateczna.
P - pole powierzchni przekroju.
,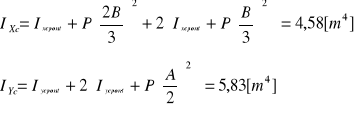
Mniejszy jest moment bezwładności względem osi X, i to jego wartość przyjmujemy do dalszych obliczeń.
Możemy teraz obliczyć wysokość metacentryczną:
![]()
= 4,58 [m4] /2,25a3 - 0,8[m] = 9,42 m - 0,8 m = 8,62 m >>2[m] - warunek stateczności pławy postawiony w zadaniu jest spełniony.
1
![]()
![]()
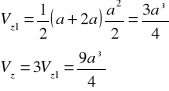
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
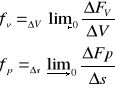
![]()
![]()
![]()
Wyszukiwarka