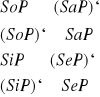LOGIKA
nauka o zasadach prawidłowego myślenia
Demokryt z abwery- pierwsze użycie słowa „logika”
Arystoteles- rozwinął to
Rozwinęła się w XV i XVI w
Najbardziej znani przedstawiciele: August Comte, David Hume, Rene Descartes, I. Kant, W. Hyell, Marks, Engels, Rojewski, Różycki (enigma)
Działy logiki
Semantyka, logika formalna, teoria poznania, metodologia nauk
Semantyka- teoria znaczeniowej strony języka, ma za zadanie walkę z nieporozumieniami, niezrozumieniami, niejasnym formułowaniem myśli, które mają swoje podłoże w wieloznacznościach i niejasnościach stwierdzeń. Umieć porozumieć się z innymi ludźmi
Logika formalna- teoria wynikania- informuje ona o tym, jakiej budowy zdania wynikają ze zdań zbudowanych w taki, a nie inny sposób. Zajmuje się budowami poszczególnych zdań
S e P ![]()
![]()
P e S
Policjant Złodziej Złodziej Policjant
Żaden policjant nie jest złodziejem ![]()
żaden złodziej nie jest policjantem
Teoria poznania - analiza prawdziwości. Zajmuje się oceną zdań pod względem ich wartości logicznej.
Metodologia nauk - zajmuje się ogólnymi metodami pracy naukowej, metodami uzasadniania twierdzeń i metodami konstrukcji systemów naukowych. Dzieli się na ogólna i szczególną.
Semantyka- nazwy, zdania, funktory- kategorie semantyczne
Kategorie semantyczne- to pewne działy wyrazów, ich zespołów i całych zwrotów językowych, wyróżnione przez logikę ze względu na znaczenie i funkcję, jaką spełniają
Nazwy- mogą zastępowa w zdaniu podmiot lub orzecznik. Za pomocą nazw można wskazać przedmiot lub osobę
Podział nazw- proste (z jednego wyrazu, np. policjant),
złożone (więcej niż jeden wyraz, np. 10- piętrowy budynek)
Desygnat nazwy- przy danym jej znaczeniu jest to przedmiot poprawnie przez tą nazwę oznaczony.
Zakres nazwy- przy danym jej znaczeniu to zespół wszystkich desygnatów danej nazwy.
Nazwy konkretne - posiadają swoje realnie istniejące desygnaty bądź też można je sobie wyobrazić, np. budynek, anioł, diabeł
Nazwy abstrakcyjne - nie posiadają swoich desygnatów ani nie można ich sobie wyobrazić, np. niebezpieczeństwo, miłość, nienawiść.
Błąd hipostazowania- użycie źle nazwy abstrakcyjnej
Nazwy oznaczające - posiadają realnie istniejące desygnaty, np. WSPol., auto, policja
Nazwy nieoznaczające - nie posiadają realnie istniejących desygnatów
Nazwy zbiorowe - których desygnaty składają się z wielu elementów, np. pluton, kompania.
Nazwy niezbiorowe - które posiadają desygnaty składające się z jednego elementu
Nazwy sprzeczne - z których jedna jest zaprzeczeniem drugiej, a suma ich zakresów stanowi zakres nazwy- klasa uniwersalna, np. policjant- nie policjant.
Klasa uniwersalna- zbiór wszystkich przedmiotów, osób i zjawisk istniejących w świecie.
Nazwy przeciwne - jedna jest zaprzeczeniem drugiej ale ich suma nie wyczerpuje zakresu nazwy klasa uniwersalna, np. policjant- cywil.
Stosunek równoważności zakresów nazw S P
S- sędzia
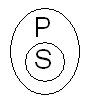
P- arbiter Stosunek podrzędności Stosunek nadrzędności
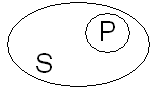
S- policjant S- policjant
P- człowiek P- policjant
ruchu drog.
Skrzyżowanie Wykluczanie
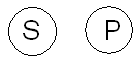

S- policjant S- policjant
P- kobieta P- złodziej
Funktory - są to wyrażenia, które nie będąc nazwami ani zdaniami służą do budowy wyrażeń bardziej rozbudowanych.
Funktory nazwotwórcze
Od jednego argumentu nazwowego, np. zdolny student
Student- nazwa (argument nazwowy)
Zdolny- funktor nazwotwórczy
Od dwóch argumentów nazwowych (od dwóch nazw), np. student i kierowca
Student, kierowca- nazwy (argumenty nazwowe)
i-funktor nazwotwórczy
Funktory zdaniotwórcze
Od jednego argumentu nazwowego, np. student myśli
Student- nazwa (argument nazwowy)
Myśli- funktor zdaniotwórczy
Od dwóch argumentów nazwowych, np. student czyta książkę
Student, książka- nazwy (argumenty nazwowe)
Czyta- funktor zdaniotwórczy
Od jednego argumenty zdaniowego, np. Nieprawda, że dzisiaj jest wtorek.
Dzisiaj jest wtorek- zdanie (argument zdaniowy)
Nieprawda, że- funktor zdaniotwórczy
Od dwóch argumentów zdaniowych, np. Pójdę do kina albo pójdę do teatru.
Pójdę do kina, pójdę do teatru- zdania (argumenty zdaniowe)
Albo- funktor zdaniotwórczy
Zdaniami w sensie logicznym określamy wyrażenia, które posiadają określoną wartość logiczną.
Czyli są prawdziwe albo fałszywe. Wynika z tego, że zdaniami w sensie logicznym mogą być zdania orzekające.
Kryteria prawdziwości zdań
Zdania coś wyrażają, czemuś przeczą, w związku z tym mają wartość logiczną.
Zdanie - każde wyrażenie, które ma wartość logiczną, to znaczy jest albo prawdziwe albo fałszywe.
Kryterium oczywistości stanu rzeczy
Kryterium praktyki społecznej
Kryterium autorytetu (zaufania do źródła)
Podział zdań ze względu na modalność:
Zdania asertoryczne
Zdania apodyktyczne
Zdania problematyczne
Zdania złożone: zdania proste, co najmniej dwa połączone funktorem, np. albo, lub, i.
Koniunkcja - zdanie złożone składające się z dwóch zdań prostych połączonych funktorem „i”, np. Warszawa jest stolicą Polski i Warszawa leży nad Wisłą.
Funktor = I
Symbol: ![]()
symbole matrycy zdań: p,q,r
Matryca prawdziwości- tabela
p |
q |
p |
p |
p |
p |
p |
f |
f |
f |
p |
f |
f |
f |
f |
Implikacja - np. Jeżeli zdam wszystkie egzaminy przewidziane regulaminem studiów WSPol, to otrzymam promocję oficerską.
Funktor: Jeżeli,… to
Symbol: ![]()
Matryca prawdziwości- tabela
p |
q |
p |
p |
p |
p |
p |
f |
f |
f |
p |
p |
f |
f |
p |
Alternatywa zwykła - np. Jan był wczoraj w kinie lub Jan był wczoraj w teatrze.
Funktor: lub
Symbol: ![]()
Matryca prawdziwości- tabela
p |
q |
p |
p |
p |
p |
p |
f |
p |
f |
p |
p |
f |
f |
f |
Alternatywa rozłączna - np. Szczytno leży na Mazurach albo jest stolicą Polski.
Funktor: albo
Symbole: ![]()
/
Matryca prawdziwości- tabela
p |
q |
p |
p |
p |
f |
p |
f |
p |
f |
p |
p |
f |
f |
f |
Zdania różnowartościowe - np. Zostanę oficerem wtedy i tylko wtedy, gdy ukończę studia wyższe.
Funktor: wtedy i tylko wtedy, gdy
Symbole: ![]()
Matryca prawdziwości- tabela
p |
q |
p |
p |
p |
p |
p |
f |
f |
f |
p |
f |
f |
f |
p |
Negacja zdań
p` lub ~p- negacja zdania (nieprawda, że p)
p |
p` |
p |
f |
f |
p |
![]()
Tautologia
To takie wyrażenie, które przy każdym podstawieniu stałych (prawda i fałsz) zamiast zmiennych zdaniowych: P, Q, R, S zawsze przechodzi w zdanie prawdziwe, np. Jeżeli znam treść zagadnień z prawa karnego, to zdam egzamin. Nie zdałem egzaminu z prawa karnego. Wynika z tego, że nie znałem treści zagadnień z prawa karnego.
p- ja znam treść zagadnień z prawa karnego
q- ja zdam egzamin z prawa karnego
wynika
przesłanki![]()
![]()
jeżeli, to funktor implikacja ogólny schemat tego uwarunkowania
p |
q |
p |
p |
p |
f |
f |
p |
f |
f |
1. 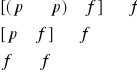
2.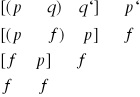
p p
3. 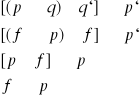
4.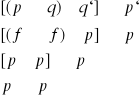
p p
Tautologia- nauka o zasadach prawidłowego myślenia
Funktory- służą tylko do budowy wyrażeń złożonych
Jeden konkretny przedmiot jest desygnatem nazwy
Zakres nazwy- wszystkie przedmioty o jednej nazwie
Treśc- cechy danego przedmiotu
Nazwa oznaczająca- ma przynajmniej jeden desygnat- zakres
Np. odnośnie krasnoludków- nazwa- nie można (nie ma krasnoludków)
Klasa uniwersalna przedmiotu- wszystko to, co istnieje na świecie.

policjant nie policjant
Polska
Ziemia stosunek wykluczenia, nie dokonujemy podziału
Europa
Szczytno
Sejm stosunek wykluczenia
poseł na sejm

nie człowieknie policjant
kierowca
dzielnicowy
przestępca
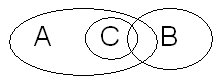
nie piesnie kierowca
sportowiec
=0
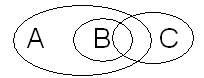
nie PolakFrancuz
Matematyk
Logiczne podstawy wnioskowania
Logika formalna- istotną rzeczą jest budowa zdań
Dwa błędy: 1. Wnioskujemy z fałszywych przesłanek
2. Błąd formalny
Dwa działy: 1. Teoria nazw
2. Teoria zdań
Ad.1 Posługujemy się zmiennymi nazwowymi S, P, M.
Posługujemy się zmiennymi p, q, r.
Tezy teorii zdań = prawa logiczne
![]()
Π -/pi/- kwantyfikator zmienny
Pierwsze prawo logiczne
Πp= ![]()
-prawo tożsamości
Dla każdego p jeżeli p, to p
Drugie prawo logiczne, tzw. prawo sprzeczności
Π ![]()
Trzecie prawo wyłączonego środka
Π ![]()
Dotyczą pary zdań sprzecznych
Z dwoma zmiennymi
Modus ponendo ponens- tryb ustanawiający przez ustanowienie
Π p, q ![]()
Dla każdego p, q, jeśli p to q i p to q.
Dla każdej prawdziwej implikacji przez ustanowienie prawdziwości poprzednika ustanawiamy prawdziwość następnika.
Mosus tolendo tollens- tryb obalający przez obalenie
Π p, q ![]()
Przez obalenie prawdziwości następnika obalamy prawdziwość poprzednika
Transpozycja prosta
Π p, q ![]()
Dla każdego p, q jeśli jeżeli p to q, jeżeli nie q, to nie p
W poprzedniku zanegowany następnik, a w następniku zanegowany poprzednik
Modus tolendo ponens- alternatywa rozłączna
Π p, q ![]()
Dla każdego p, q
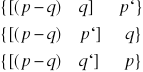
Prawa De Morgana
1. ![]()
Π p, q ![]()
2. Π p, q ![]()
Teoria nazw
Zajmuje się tylko klasycznymi zdaniami kategorycznymi, tj. zdanie składa się z podmiotu i orzecznika połączonych łącznikami.
Cztery rodzaje schematu: S a P, S i P, S e P, S o P
S a P- każde S jest P a- każde jest
S e P- żadne S nie jest P e- żadne nie jest
S i P- niektóre S są P i- niektóre są
S o P- niektóre S nie są P o- niektóre nie są
nieprawda- nawias i przecinek u góry
Ze względu na ilość: ogólne, szczegółowe
Ze względu na jakość zdania kategorycznego: szczegółowo-przeczące, szczegółowo-twierdzące
S a P |
S e P |
Ogólne |
S i P |
S o P |
szczególne |
Twierdzące Przeczące
Termin rozłożony- ten, który występuje w zdaniu w całym zakresie
Rozłożone są podmioty zdań ogólnych i orzeczniki zdań przeczących
Wnioskowania bezpośrednie- jedno z drugiego
Wnioskowania pośrednie- 2 zdania kategoryczne stanowią przesłanie a 3-e jest wnioskiem
Bezpośrednie: konwersja, obwersja, opozycja w zdaniu

Konwersja- na podstawie określonej relacji między podmiotem i orzecznikiem wnioskujemy o relacji między samym orzecznikiem a podmiotem
S R P ![]()
P R S
Np. S a P![]()
P i S- tzw. konwersja z ograniczeniem
S i P ![]()
P i S konwersja prosta
S e P ![]()
P e S
Polegają na zamianie miejscami podmiotu z orzecznikiem
Obwersja- na podstawie określonej relacji w zdaniu kategorycznym między podmiotem i orzecznikiem wnioskujemy o relacji między nimi
![]()
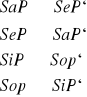
Podmiot bez zmian, zmienia się orzecznik i zaprzeczamy rodzaj zdania kategorycznego.
Opozycja zdań- wnioskowanie z kwadratu logicznego
Graficzne przedstawienie zależności pomiędzy zdaniami kategorycznymi. Po lewej zdania przeczące po prawej- twierdzące.

![]()
![]()
![]()
Przeciwieństwo: mogą być jednocześnie fałszywe
nie mogą być jednocześnie prawdziwe
![]()
Podprzeciwieństwo: mogą być jednocześnie prawdziwe
nie mogą być jednocześnie fałszywe
![]()
Nadrzędność: zdanie ogólne jest prawdą, szczególne też jest prawdą
![]()
Podrzędność: zdanie podrzędne fałszywe, fałszywe nadrzędne
![]()
Sprzeczność: 2 zdania sprzeczne nie mogą być jednocześnie prawdziwe lub fałszywe
|
|
Sprawdzi czy schemat jest prawem logicznym- tautologią.
![]()
ilość sprawdzeń 2n (n- ilość zmiennych)
p |
q |
r |
p |
p |
p |
p |
p |
f |
p |
f |
p |
p |
f |
f |
f |
p |
p |
f |
p |
f |
f |
f |
p |
f |
f |
f |
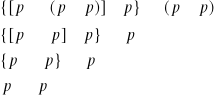
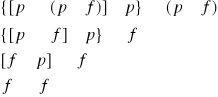
Zadanie
Warunkiem przyjęcia skargi rewizyjnej jest zachowanie terminu i złożenie skargi przez osobę uprawnioną, co wynika z faktu nie przyjęcia skargi
![]()
![]()
osoba nieuprawniona, ale w terminie
osoba uprawniona, nie w terminie
osoba nieuprawniona, nie w terminie
jeżeli ktoś kradnie mienie społeczne, to nie jest uczciwy. Jan nie kradnie mienia społecznego, więc jest uczciwy.
![]()
q = p
p = f
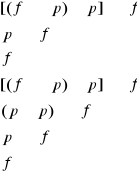
q = p p = f
Jeżeli Jan ma pozamałżeńskie dziecko, to jeżeli sąd ustalił jego ojcostwo, musi on płaci na utrzymanie alimenty. Z tego wynika, że jeśli Jan ma pozamałżeńskie dziecko i musi płacic alimenty, to sąd ustalił jego ojcostwo.
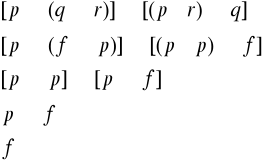
q = f
p = p tylko dla tych zmiennych wzór jest
r = p fałszywy
Temat: Błędy i nieporozumienia w słownym przekazywaniu myśli i odbiorze informacji.
Najczęściej popełniane błędy w formułowaniu myśli i odbiorze informacji.
Stosowanie niewłaściwej supozycji (roli znaczeniowej) nazw, np. wąż: zwierzę, gatunek, słowo 3-literowe
Używanie wyrażeń okazjonalnych: on, to, wtedy, tam, tak
Używanie eufemizmów, np. ta twoja żona to najpiękniejsza to nie jest (nie najpiękniejszy, nie najmądrzejszy- rozumiemy nie w przenośni ale dosłownie)
Odpowiednia intonacja głosu, np. ale ty to jesteś mądry- złośliwie
Właściwe i przenośne znaczenie wyrazów (rozumowanie dosłowne, a nie w przenośni)
Aktualne i potencjalne znaczenie czasowników, np. Władek pięknie śpiewa- głośno na całą wieś lub aktualnie
Ekwiwokacja- błąd logiczny polegający na tym, że mówiący jakieś zdanie używa wyrażenia wieloznacznego w różnych jego znaczeniach, uważając, że używa go jednoznacznie, np. na stare lata, na młode lata; miedź jest cennym metalem, cenne metale powinniśmy przechowywać w kasie pancernej
Amfibologia- błąd logiczny polegający na tym, że wyrażenie jest wieloznaczne ze względu na jego strukturę, np. jechać dalej nie wolno zatrzymać się (nie wiadomo, czy jechać czy stać)
Nie ostry zakres wyrażeń językowych
Niejasność treści wyrażeń
Wypowiedź niezręczna
Stosowanie wyrażeń niezrozumiałych
Brak kwantyfikacji- dokładności danej
Niedopowiedzenia
Traktowanie wypowiedzi przenośnych jako ostatecznych
Absurd- wyrażenie sprzeczne wewnętrznie, czyli takie można przedstawi według schematu: istnieje taki x, że x jest a oraz x nie jest a, np. Jan jest bezdzietnej matki (wynika z tego, że pewna kobieta jest matką i nie jest matką)
Nonsens- wyrażenie nieskładne, czyli bezładne schematycznie, np. student są nad niekiedy
Temat: Wnioskowania ze zmiennymi nazwowymi
|
S a P |
S e P |
S o P |
S i P |
|
p |
f |
f |
p |
|
f |
f |
p |
p |
|
p |
f |
f |
p |
|
f |
f |
p |
p |
|
f |
p |
p |
f |
![]()
2 razy obwersja
2 razy konwersja
Każda nauka jest trudem. Otrzymać zdanie. Żaden nie trud nie jest nauką.
![]()
Niektóre czyny człowieka są przestępstwami. Nieprawda, że żadne przestępstwo nie jest czynem człowieka.
![]()
Uznając za prawdziwe zdanie: „Każda zbrodnia jest przestępstwem”. Ustal wartość logiczną zdania. Niektóre nie są przestępstwem, niektóre nie są zbrodnią.
p- przestępstwa
s- zbrodnia ![]()
(P` o S`) = ?
Wyprowadzi wszystkie wnioski ze zdania: „Żaden człowiek nie jest nieomylny”
S P
![]()
Żaden P- nieomylny nie jest człowiekiem
![]()
Każdy człowiek jest omylny
![]()
Nieprawda, że każdy człowiek jest nieomylny
![]()
Niektórzy ludzie nie są nieomylni
![]()
Nieprawda, że niektórzy ludzie są nieomylni
Temat: Wnioskowanie pośrednie.
Przesłanka większa termin średni
P R M
S R M przesłanki jest to sylogizm kategoryczny
S R P wniosek
Termin mniejszy termin większy
Wnioskowanie proste: podane przesłanki- szukamy wniosku.
Entymemat- podany wniosek i jedna z przesłanek. Szukamy brakującej przesłanki.
8 znamion wadliwości
W sylogizmie powtarza się maksymalnie 3 terminy. Jeżeli więcej- fałsz.i o o i
o i o i układ błędny- nie można wnioskować
3. Obydwie przesłanki muszą być przeczące e o e o
e o o e
4. Termin rozłożony- musi być przynajmniej w jednej przesłance
5. Wniosek nie może być twierdzący jeżeli któraś z przesłanek jest przecząca.
6. Wniosek nie może być ogólny gdy któraś z przesłanek jest zdaniem szczegółowym
![]()
7. Wniosek nie może być przeczący gdy żadna z przesłanek nie jest przecząca
![]()
8. Termin mniejszy lub większy jest rozłożony we wniosku to musi być rozłożony w przesłance
P a M
S o M
S o P
Wnioskowanie entymematyczne (rozłożone)
Myślę, więc jestem- podmiot domyślny- Ja myślę, więc ja jestem
M ułamek P S M S P
![]()
M- myślę M a P P a M
P- jestem S a M S a M
S a P S a P
Termin rozłożony tzn. użyty w zdaniu w całym swoim zakresie
Niektóre ptaki są wróblami, bo każdy wróbel ma skrzydła.
wniosek
P- przesłanka szyk w zdaniu
W- wniosek
P wynika z tego W
a więc
to
dlatego, że
W ponieważ P
bo
![]()
P- wróbel P a M P a M
M- skrzydła S ai M lub M ai S
i- niektóre są S i P S i P
S- ptak
Temat: Cwiczenia- wnioskowanie.
Dwie nazwy w miarę proste- co to za nazwy? Np.
Inteligentna blondynka: złożona, oznaczająca, konkretna, niezbiorowa
![]()
Policjant sportowiec- krzyżowanie
Nie policjant- A- A`- policjant można tak
Nie Polak- B- B`- Polak
Dzielnicowy- C- C`- nie dzielnicowy

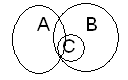
Trzecie- krótkie zdanie: zaznaczy w nim funktory: Do pokoju wszedł policjant i oficer. (można potraktowac, że weszła jedna lub dwie osoby).
4. Sprawdzi czy wnioskowanie jest poprawne.
Temat: Logiczne podstawy argumentowania
Argumentowanie- czynność zmierzająca do wywołania u kogoś określonych przeświadczeń lub ocen czy dążeń.
Bądź przekonany, że tak i tak bo to i tamto
żądanie nasza teza argument
erystyka- z gr. eris- nauka prowadzenia sporów, dyskutowania, obalania argumentów przeciwnika i wykazywania słuszności własnych tez
dyskusja- wymiana poglądów
Prawidłowe (lojalne) chwyty erystyczne
Przerzucanie ciężaru dowodu na barki przeciwnika
Wyszukanie słabych punktów w wypowiedziach przeciwnika i stawianie im zarzutów
Atakowanie założeń przeciwnika a nie samych tez wynikających z tych złożeń
Wnioskowanie z tego, co przeciwnik uznał za prawdziwe
Zabranie głosu w odpowiednim momencie dyskusji
Nieuczciwe (nielojalne) chwyty erystyczne
Nieżyczliwa interpretacja wypowiedzi przeciwnika
Wyciąganie nieuzasadnionych wniosków z wypowiedzi przeciwnika
Przedstawienie w niekorzystnym świetle osoby przeciwnika, np. ośmieszenie
Uciekanie się do demagogii, argumentów nierzeczowych albo rozbudzających emocje u słuchaczy czy nieznających się na danej tematyce
Odwoływanie się do próżności jakiejś osoby i posługiwanie się pochlebstwem
Odwoływanie się do uczucia litości
Bazowanie na nieświadomości przeciwnika
Bazowanie na strachu przeciwnika
Zwracanie się nie do przeciwnika lecz do ogółu zebranych
Straszenie pobiciem
Zastraszenie pogorszeniem sytuacji materialnej
12
Wyszukiwarka