Część I
PRZEPISZ STARANNIE - ZWRACA NA TO UWAGE, PRZEPISZ TAK ŻEBY PRACA NIE BYŁA PODOBNA - INNI MOGĄ MIEC TAKIE SAME I CO WTEDY?
Zadanie 1 - wyprowadzenie równań równowagi płynu.
Rozważamy dowolną przestrzeń ![]()
wypełnioną płynem idealnym
![]()
![]()
![]()
![]()
![]()
![]()
![]()
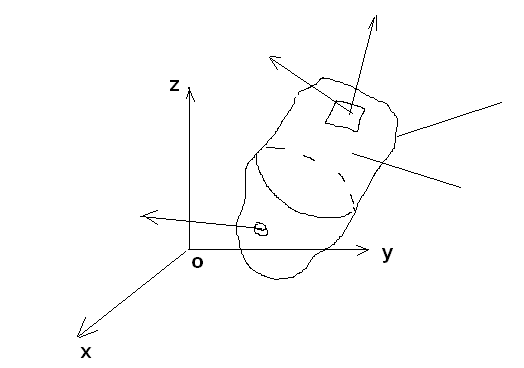
- wnętrze obszaru
![]()
![]()
- powierzchnia ograniczająca obszar
ds - elementarny wycinek powierzchni dV - elementarny wycinek wnętrza obszaru
ΔFp - jednostkowa siła powierzchniowa
![]()
ΔFv - jednostkowa siła objętościowa
![]()
- wektor normalny do wycinka ds.
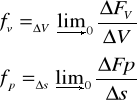
- gęstość sił objętościowych
- gęstość sił powierzchniowych
Siły powierzchniowe zależą od usytuowania rozpatrywanej powierzchni, nie są zatem wielkością stałą i niezależną. Niezależnie od doboru powierzchni opisywał będzie stan cieczy tensor napręzeń- charakteryzujący naprężenia w danym punkcie. Na jego wartości nie ma wpływu sposób doboru powierzchni.

- tensor naprężeń
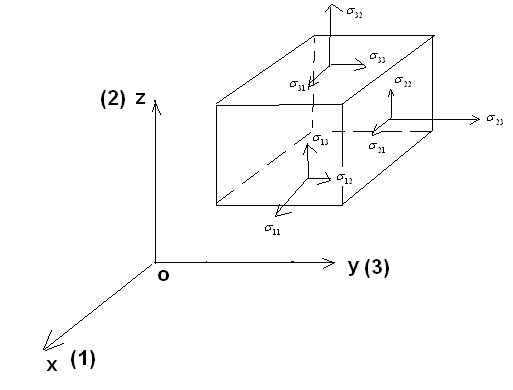
Ze względu na równości odpowiednich naprężeń stycznych, macierz ta jest macierzą symetryczną, czyli: ![]()
, ponieważ ![]()
.
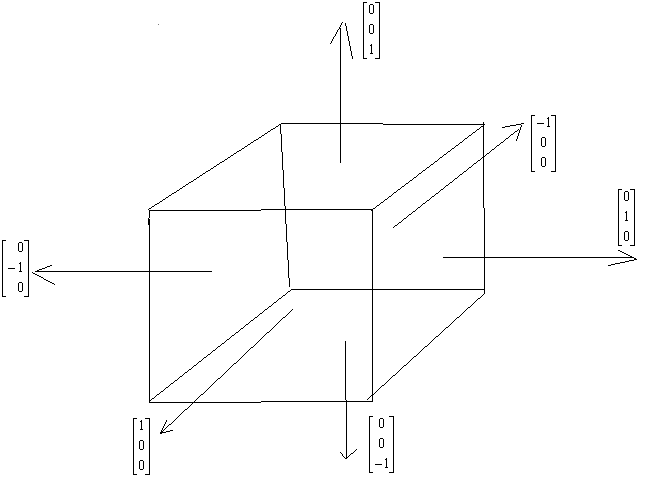
![]()
Rysunki przedstawiają elementarny wycinek obszaru Ω- czyli d Ω, oraz jego naprężenia i współrzędne wektora
![]()
Są to makroskopowe ujęcia punktu obszaru. Można spostrzec ze na jego powierzchnię działają siły powierzchniowe zależne od doboru powierzchni. Ściana powierzchni opisywana jest przez wektor
Ogólny stan naprężenia w danym punkcie przedstawia tensor naprężeń σ Siła powierzchniowa będzie zatem równa:
![]()
- jest to wektor [N/m] = [Pa]
(R3) (R3x3) (R3)
Znalezienie siły wypadkowej wymaga scałkowania po powierzchni:
![]()
; [N]
Analizując budowę tensora σ zauważymy, że:
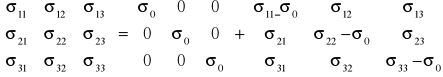
Tensor σ tensor kulisty tensor dewiatorowi - σD
Gdzie: ![]()
; oraz ![]()
- ślad macierzy σ
Tensor kulisty to 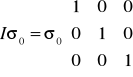
Czyli ostatecznie: ![]()
Tensor kulisty odpowiedzialny jest za opis matematyczny wszechstronnego ściskania/rozciągania. Dewiator jest wyrażeniem związanym ze zmianą postaci ciala - ścinaniem. Ponieważ przy rozpatrywaniu płynu nie możemy mowić o rozciąganiu, a σ0 ma kierunek naprężeń rozciągających, to ma on zawsze wartość ujemna. Wartość tę nazywamy ciśnieniem.
![]()
; ![]()
; ![]()
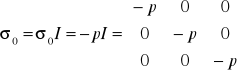
Po uwzględnieniu założenia, że siła powierzchniowa w każdym kierunku jest jednakowa i skierowana prostopadle do powierzchni, to dla danej chwili:

![]()
Jest to całka wektoru
Rozważając kolejno siły objętościowe:
![]()
[N/m3] - gęstość siły objętościowej.
Są to siły wewnętrzne, wzajemne. Obliczamy ich wypadkową dla danej chwili:
![]()
Siła wypadkowa w całym obszarze to ![]()
:
![]()
Na mocy Twierdzenia Gaussa-Ostrogradskij-ego możemy zastąpić całkę powierzchniową całka objętosciową w poniższy sposób:
![]()
Aby zachowana była równowaga to: ![]()
dla każdego obszaru Ω czyli:
![]()
![]()
Musi tak być dla każdego obszaru Ω 0 (ponieważ równie dobrze wymagać można zachowania równowagi i tego obszaru). Zależność ![]()
= 0 nazywamy równaniem równowagi ośrodka ciągłego, lub równaniem Eulera. Obowiązuje ono dla płynu nielekkiego.

, a wtedy: 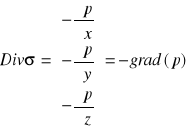
Możemy zatem napisać równanie równowagi dla płynu:
Ponieważ:![]()
, oraz ![]()
to ostatecznie:
![]()
Dla zachowania pełnej równowagi spełnione musi być też równanie momentów.
![]()
Po przekształceniach analogicznych do tych z warunku na równowagę sił, możemy zauważyć że jeżeli siłą wypadkowa będzie równa zeru, to niezależnie od tego na jakim ramieniu będzie działała, również da moment równy zeru. A zatem warunkiem wystarczającym do spełnienia aby ośrodek był w równowadze, jest zależność:
![]()
![]()
Jest to warunek równowagi płynu doskonałego.
Zadanie 2 - cysterna
L= |
9,2 |
[m] |
|
|
|
|
D= |
2,2 |
[m] |
|
|
|
|
d= |
1 |
[m] |
|
|
|
|
ρmleka= |
1300 |
[kg/m3] |
|
|
|
|
a= |
0,3 |
g |
|
Współrzędne klapy: |
|
|
g= |
9,81 |
[ms2] |
|
Xk= |
4,6 |
klapa dolna |
Pa= |
101325 |
[Pa] |
|
Yk= |
0 |
|
Znajduję siły objętościowe działające na ciecz w poruszającej się cysternie:
Siła ciężkości: fg =ρ g
Sila bezwładności fb = - ρ a ( skierowane przeciwnie do przyspieszenia cysterny - czyli zgodnie z kierunkiem osi x )

[N/m3] - jest to wektor wypadkowy sił objętościowych, obliczam jego współrzędne:
fx= |
3826 |
fy= |
-12753 |
fz= |
0 |
Mając współrzędne możemy usytuować wektor wypadkowy w płaszczyźnie cysterny. Wektor wskazuje kierunek najszybszego wzrostu cisnienia, po przeciwnej stronie jest kierunek spadku. W rogu, wskazywanym przez kierunek spadku ciśnienia znajduje się pęcherzyk powietrza, panuje w nim ciśnienie atmosferyczne.
Linie prostopadłe do wektora wypadkowego to izobary - linie stałego ciśnienia.
Wiemy, że: ![]()
- równanie równowagi dla płynu
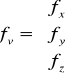
natomiast 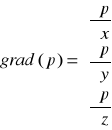
czyli z tego wynika, że: ![]()
A zatem możemy napisać korzystając z różniczki zupełnej:
![]()
ale ponieważ ![]()
to w każdym otoczeniu punktow o współrzędnych x,y,z pochodne cząstkowe są stałę i możemy zastąpić: ![]()
, ![]()
![]()
i napisać równanie ciśnień w postaci:
![]()
I wtedy: p(x,y,z) =
p(x,y,z) = |
3826 |
x + |
-12753 |
y + |
0 |
z + c |
C - obliczamy z warunku brzegowego na ciśnienie atmosferyczne w punkcie gdzie znajduje się pęcherzyk powietrza.
Współrzędne punktu pęcherzyka to:
Xp= |
0 |
Yp= |
2,2 |
Czyli p( xp, yp) = 101325 =3826 xp - 12753 yp + c
Po obliczeniu:
c= |
129382 |
[Pa] |
Równanie ciśnienia ma następującą postać:
p(x,y,z) = |
3826 |
x + |
-12753 |
y + |
129382 |
|
|
|
|
|
|
Aby znaleźć siłę naporu mleka na klapę należy obliczyc ciśnienie w punkcie środka ciężkości tej klapy, a następnie pomnożyc je przez pole powierzchni tej klapy:
Współrzędne klapy: |
|
|
|
|
|
Xk= |
4,6 |
klapa dolna |
p(xk, yk)= |
146981 |
[Pa] |
Yk= |
0 |
|
|
|
|
Aklapy=πd2/4= |
0,79 |
[m2] |
|
|
|
F=A*p(xk, yk)= |
114645 |
[N] |
-odpowiedź |
||
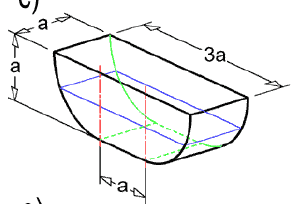
Zadanie 2 - pława
H0= |
1,35 |
[m] |
m0= |
210 |
[kg] |
δ= |
0,003 |
[m] |
ρstali= |
7400 |
[kg/m3] |
ρwody= |
1000 |
[kg/m3] |
g= |
9,81 |
[m/s2] |
Najpierw obliczam objętość zanurzoną, masę i siłę wyporu pontonu, i zestawu pontonów:
(Promieniem zaokrągenia jest wartość a, ponton jest zanurzony do polowy swojej wysokosci)
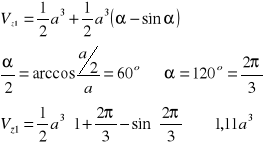
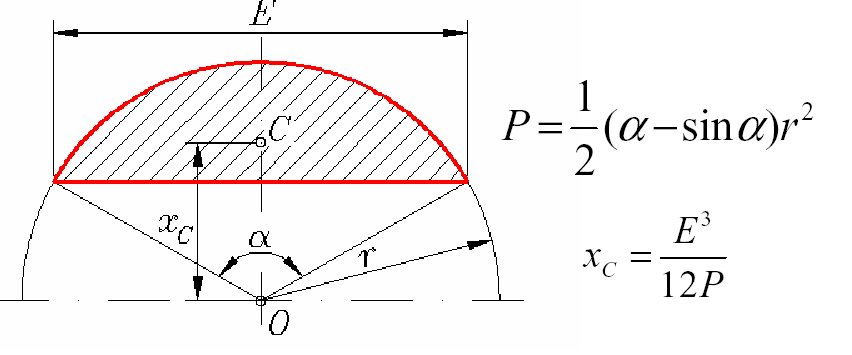
![]()
Vz = 6 Vz1 = 6,66a3
M = 4 M1 = 1638 a2
![]()
65335 a3
Równanie równowagi układu:
![]()
65335 |
a3 |
= |
16069 |
a2+ |
2060 |
|
65335 |
a3 |
- |
16069 |
a2 - |
2060 |
=0 |
Za pomocą Excela obliczam wartości dla kolejnych wartości parametru a i znajduję pierwsze dodatnie rozwiązanie. Wartość dokładna rozwiązania to 0,418 m, przyjmuję do dalszych obliczeń wartość a = 0,42 [m]. Następnie trzeba obliczyc polozenie środka ciężkości pontonów, zestawu pontonów i pławy oraz srodka wyporu. Pontony nie są symetryczne względem płaszczyzny poziomej.
Ponton:
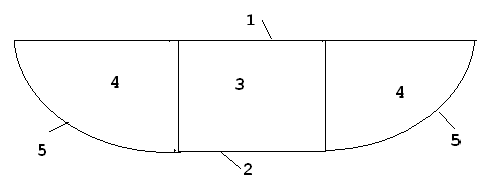
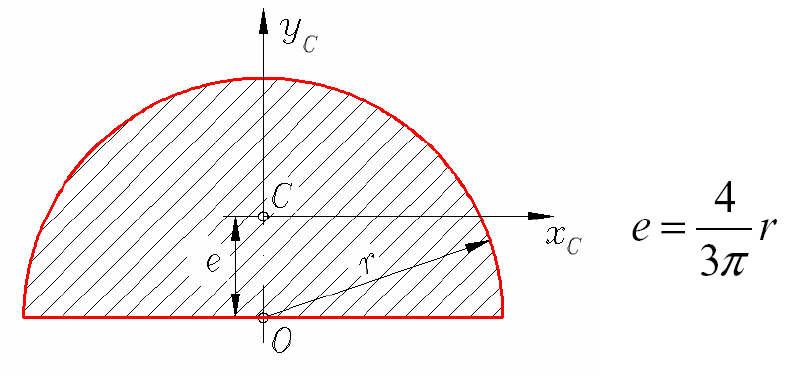
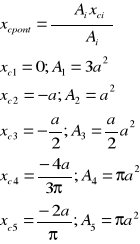
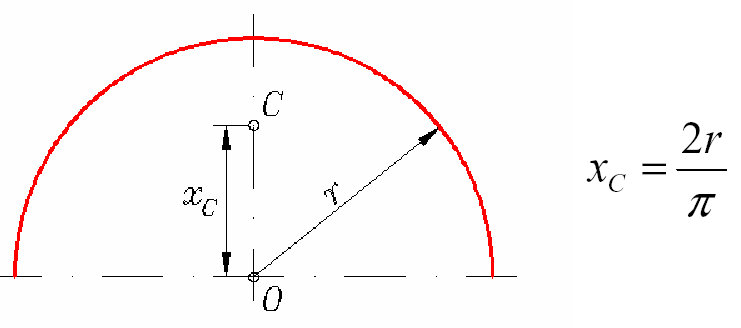

-0,164
Srodek ciężkości całego pontonu jest zlozeniem srodkow ciężkości wszystkich ścian pontonu.
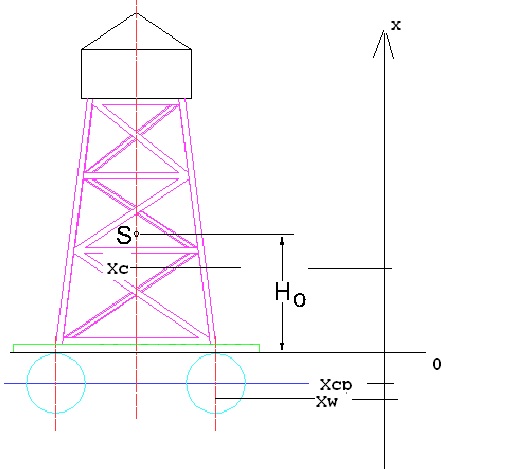
xc pont= |
-0,164 |
[m] |
M= |
289 |
[kg] |
xc plawy=Ho= |
1,35 |
[m] |
m0= |
210 |
[kg] |
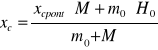
xc= |
0,473 |
[m] |
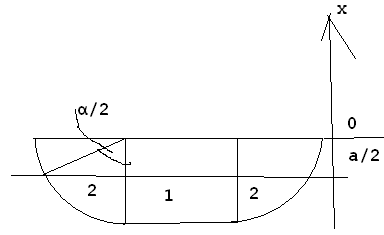
Środek wyporu pontonu obliczam jako środek ciężkości objętości zanurzonej pontonu, przy czym zgodnie z założeniem, ponton przyjmuję zanurzony do polowy swojej wysokości.

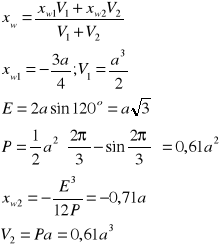

-0,3 [m]
Odległość pomiędzy środkiem wyporu i środkiem ciężkości:
lm=|xcxw|= |
0,77 |
[m] |
Obliczam momenty bezwładności przekroju względem jego głównych centralnych osi bezwładności. Przekrój zanurzeniowy pontonu jest prostokątem o bokach a i 2,73 a (ponieważ ponton jest ostrosłupem o podstawie trapezu zanurzonym do polowy wysokości -w sposób jak na rysunku w tresci zadania)
- pole powierzchni przekroju zanurzeniowego
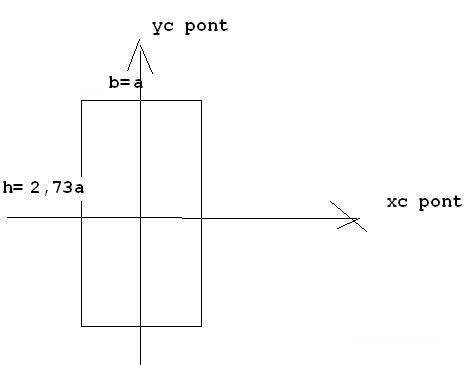
![]()
0,0526[m4]
![]()
0,0072 [m4]
Obliczam momenty bezwładności układu pontonów względem głownej centralnej osi bezwładności (ze względu na symetrię promienista układu momenty względem innych osi przechodzących przez środek symetrii będą takie same)
Przyjmuję promień rozstawu pław r = 2 m
Moment pontonu obróconego i odsuniętego od osi X obliczam następująco;
e = r sin 60o = 1,73 [m]
A = 2,73 a2 = 0,48 [m2]
- pole powierzchni przekroju zanurzeniowego
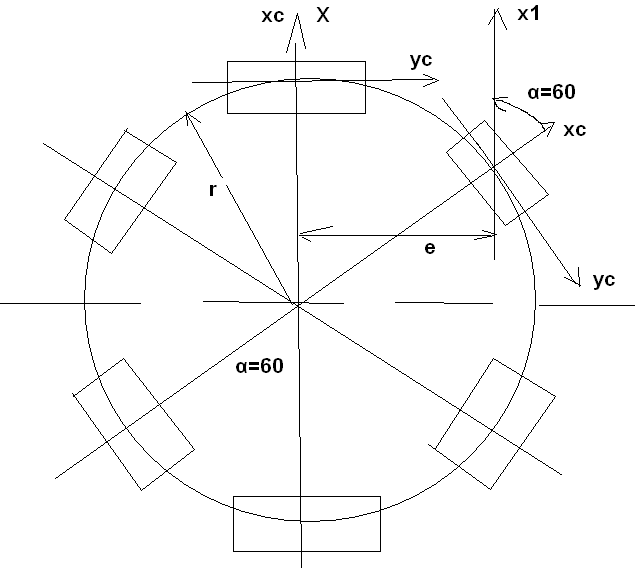
IX1 = Icxc cos2 60o + Icyc sin2 60o = 0,0185 [m4]
IX = Iy1 + Ae2 = 0,0185 + 0,48 *1,73 2 = 1,45 [m4]
Moment całego zestawu pontonów:
IcX = 2 Icxc + 4 I X = 5,8 [1m4]
Momenty względem pozostałych osi będą równe,
Więc jest to zarazem jedyny i najmniejszy moment
bezwładności tej pławy.
Możemy teraz obliczyć wysokość metacentryczną:
![]()
= 5,81 [m4] / 6,66a3 - 0,77 [m] = 11,78m - 0,77 m = 11,01m >>2[m]
- warunek stateczności pławy postawiony w zadaniu jest spełniony.
1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
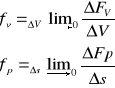
![]()
![]()
![]()
Wyszukiwarka