ĆWICZENIE NR 4

Dokładne kryteria stabilności lokalnej

4.1. Równanie stanu i macierz stanu:

Jak wspomniano na początku stabilność lokalna jest stabilnością układu nieliniowego przy działaniu małych zakłóceń. Można ją badać na podstawie I zasady Lapunowa, z której wynika, że stan ustalony układu nieliniowego jest stabilny lokalnie, jeżeli zlinearyzowany w tym punkcie układ równań różniczkowych jest stabilny.

Do pełnego opisu SEE potrzebne są następujące równania różniczkowo- algebraiczne:

• równania różniczkowe opisujące ruch wirników, układy wzbudzenia i regulacji napięcia, turbiny i ich regulatory prędkości:

(41)

gdzie x- to zmienne stanu, y- pozostałe zmienne

• równania algebraiczne nieliniowe wynikające z praw Ohma i Kirchhoffa, opisujące rozpływy mocy w systemie:

(42)

W wyniku linearyzacji otrzymujemy układ równań macierzowych:

(43)

(44)

Z równania (44) wynika, że:

Δy= -A_yy^-1A_yxΔx (45)

podstawiając (48) do (46) otrzymujemy:

(46)

gdzie: A - jest macierzą stanu nazywaną również macierzą systemową.

Szczegółowa analiza macierzy stanu wskazuje, że jest to macierz niesymetryczna rzadka. Jej wymiar jest zależny od liczby generatorów w systemie oraz od liczby równań różniczkowych opisujących stan nieustalony pojedynczego generatora wraz z regulatorem napięcia i regulatorem prędkości turbiny.

4.2. Wartości własne i wektory własne macierzy stanu:

Przy badaniu stabilności lokalnej bardzo ważne są tzw. wartości własne i wektory własne prawo- i lewostronne macierzy stanu A. Wartości własne wyliczamy z równania charakterystycznego macierzy stanu podanego poniżej:

det (A-λI) = 0 (47)

gdzie: I- macierz jednostkowa.

W wyniku rozwiązania równania charakterystycznego otrzymujemy wektor wartości własnych λ. Poszczególne wartości własne mogą być liczbami zespolonymi lub rzeczywistymi.

Wektorem własnym prawostronnym macierzy A nazywamy wektor m_i o składowych rzeczywistych lub zespolonych spełniający następujące równanie macierzowe:

Am_i=λ_im_i (48)

gdzie wektor własny prawostronny, odpowiadający wartości własnej λ_i:

m_i=
(49)

Jeśli przez M oznaczymy macierz, której kolumnami są wektory prawostronne macierzy A

M= [m₁ ... m_i ... m_n]
(50)

a przez Λ macierz diagonalną wartości własnych:

Λ=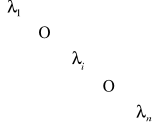
(51)

to można będzie zapisać, że

AM = MΛ (52)

Podobnie postępujemy przy wyznaczaniu wektorów własnych lewostronnych macierzy A, a mianowicie:

n
A=λ_i n
(53)

gdzie wektor własny lewostronny:

n
=[n_i1 ... n_ii ... n_in] (54)

Ogólnie można więc zapisać, że:

NA= ΛN (55)

gdzie macierz N to macierz której wierszami są wektory własne lewostronne n

N=
( 56)

Po uwzględnieniu powyższych zależności macierz stanu przedstawić można jako iloczyn trzech macierzy: macierzy wektorów własnych prawostronnych M, macierzy diagonalnej wartości własnych Λ i macierzy wektorów własnych lewostronnych N:

A= MΛM^-1= MΛN (57)

Ogólną postać rozwiązania równania stanu można zapisać następująco:

Δx(t)=M e^Λtz₀=M e^ΛtNx₀ (58)

Natomiast dla konkretnej zmiennej stanu Δx_i równanie powyższe przyjmuje postać:

Δx_i(t)=
(59)

Odpowiedź systemu na małe wymuszenie jest określona przez wartości własne i wektory własne macierzy stanu. Zespolone wartości własne leżące w prawej półpłaszczyźnie powodują rosnące oscylacje, w lewej półpłaszczyźnie - malejące oscylacje. Dodatnie części rzeczywiste wartości własnych powodują wykładniczy wzrost wartości zmiennej stanu, a ujemne części - monotoniczne zanikanie. Warunkiem stabilności lokalnej jest wiec, by wszystkie wartości własne macierzy stanu A miały ujemne części rzeczywiste . Ponieważ części rzeczywiste wartości własnych decydują o tłumieniu oscylacji, zatem chodzi o to, aby wartości własne znajdowały się w lewej półpłaszczyźnie liczb zespolonych - możliwie jak najdalej od osi liczb urojonych. Można to osiągnąć m. in. poprzez zmianę parametrów układów regulacji [2].

Aby właściwie dokonać zmiany parametrów układu regulacji należy najpierw ocenić jaki jest stopień wrażliwości danej wartości własnej na zmianę konkretnego parametru układu regulacji. Sposób ten w skrócie przedstawiono poniżej.

Zgodnie ze wzorem (53) można zapisać, że:

(53)

Po pomnożeniu tego równania przez wektor własny prawostronny m_i, otrzymamy:

(60)

czyli

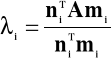
(61)

Jeśli przez p oznaczymy parametr układu regulacji (np. stała czasowa lub współczynnik wzmocnienia wybranych członów regulatora) to wrażliwość wybranej wartości własnej na zmianę parametru p określimy licząc pochodną cząstkową konkretnej wartości własnej po konkretnym parametrze układu regulacji:

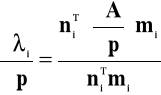
(62)

Jeśli założymy, że parametr p równa się elementowi a_jj (pochodna macierzy stanu względem tego elementu jest równa macierzy zerowej za wyjątkiem pozycji a_jj=1) to wzór (62) przyjmuje postać:

(63)

Współczynnik c_ij jest właśnie poszukiwanym przez nas współczynnikiem udziału zmiennej stanu j w wartości własnej λ_i. Pozwala on ocenić, z którymi zmiennymi stanu jest najsilniej związana dana wartość własna.

1. Opis modelu układu wzbudzenia i regulacji napięcia generatora oraz

turbiny wraz z regulatorem prędkości:

W stanie nieustalonym na pracę generatora synchronicznego mają wpływ następujące układy regulacji:

• układ regulacji wzbudzenia i regulacji napięcia generatora,

• układ regulacji prędkości turbiny.

W równaniach generatora zmianę wzbudzenia uwzględnia się za pomocą sem wzbudzenia e_f, która ulega zmianom w czasie trwania stanu nieustalonego, stosownie do dynamiki układu wzbudzenia i regulacji napięcia. Schemat ogólny układu wzbudzenia i regulacji napięcia pokazano na rysunku 13:

Rys.13 Schemat funkcjonalny układu wzbudzenia i regulacji napięcia generatora[2].

W skład układu wzbudzenia i regulacji napięcia wchodzą następujące człony funkcjonalne:

• człon pomiarowy to układy pomiarowo-porównawcze zbudowane na przetwornikach sygnałów. Zwłoka czasowa członu pomiarowego T_r jest zwykle pomijana.

• regulator to układ wzmacniaczy magnetycznych lub elektronicznych z ogranicznikami chroniącymi wzbudnicę i generator przed przekroczeniem dopuszczalnych technicznie warunków pracy.

• człon korekcyjny jest to układ pracujący w pętli sprzężenia zwrotnego względem napięcia wzbudnicy. Jego zadaniem jest stabilizacja regu­lacji napięcia.

• stabilizator systemowy, oznaczany skrótem PSS, dostarcza sygnał uzależniający uchyb regulacyjny od zmian mocy lub prędkości wirowania po to, aby poprawić tłumienie kołysań wirnika. Regulatory napięcia mogą bowiem powodować powstanie słabo tłumionych oscylacji kąta wirnika.

• wzbudnice które można podzielić na wirujące i statyczne. Wzbudnice wirujące to wzbudnice prądu stałego lub wzbudnice prądu zmiennego z prostownikami.

W przypadku badania stabilności systemu SEE oraz wpływu parametrów regulatorów napięcia na stabilność, regulator napięcia należy opisać równaniami różniczkowymi. Równania te (razem z równaniami ruchu wirnika turbozespołu oraz równaniami rozpływu mocy w systemie) opisują jednoznacznie stan SEE i pozwalają (np. po zlinearyzowaniu) na badanie stabilności pracy systemu.

Poniżej przedstawiono schemat turbiny wraz z regulatorem prędkości.

Rys. 14 Schemat układu pracy turbiny wraz z regulatorem prędkości[2].

Nowoczesne układy regulacji prędkości obrotowej turbin mogą oddziaływać na przebiegi nieustalone elektromechaniczne. Szybkie zamknięcie zaworu dolotowego pary może stłumić kołysania wirników. Wyróżnia się dwa typy regulatorów turbinowych:

• regulatory mechaniczno- hydrauliczne mają z reguły luzy w układach dźwigni mechanicznych, co powoduje opóźnienie ich działania o około 0,2-0,3 s,

• regulatory elektrohydrauliczne które praktycznie nie mają zwłoki w działaniu.

Uzyskane (w oparciu o działanie regulatorów) równania należy dołączyć do układu równań różniczkowych modelujących ruch wirnika, równań różniczkowo- algebraicznych opisujących stan nieustalony w generatorze oraz równań różniczkowych wzbudzenia i regulacji napięcia.

4.4. Badanie stabilności lokalnej systemu generator- sieć sztywna:

Rozpatrzmy układ przestawiony na rysunku 15 poniżej:

Rys. 15 Układ przesyłowy generator- sieć sztywna [2]: a) schemat ideowy, b) schemat

zastępczy przed eliminacją odbioru, c)schemat zastępczy po eliminacji odbioru.

W SEE pokazanym na rysunku 15 można wyodrębnić generator zasilający pobliskie odbiory oraz współpracujący poprzez linie i transformatory z pozostałą częścią systemu traktowaną jako sieć sztywna. Otrzymany w ten sposób SEE można opisać układem równań różniczkowo- algebraicznych. Równania różniczkowe są związane z równaniami ruchu wirnika, równaniami regulacji obwodu wzbudzenia i regulacji napięcia oraz regulacji prędkości turbiny. Równania algebraiczne są nieliniowe i opisują rozpływy mocy w systemie.

Nieliniowość równań rozpływów mocy jest związana z posługiwaniem się mocami, a nie prądami węzłowymi. Jeśli moce odbiorów zastąpimy admitancjami, moce generatora- prądami, to otrzymamy układ liniowych równań węzłowych. Obliczenia prowadzi się w jednostkach względnych. Kolejność obliczeń jest następująca:

• obliczyć rozpływy mocy, rozwiązując iteracyjnie nieliniowy układ równań węzłowych napięciowo- mocowych.

• obliczyć składowe prostokątne napięcia U_a, U_b oraz prądu generatora I_a, I_b.

• wyznaczyć kąt wirnika generatora δ w stanie ustalonym jako fazę początkową sem E_Q.

• przetransformować napięcia i prądy generatora do układu d, q, aby otrzymać U_d, U_q oraz I_d, I_q.

• wyznaczyć sem w stanie przejściowym E'_d oraz E'_q, włączone za reaktancją przejściową X'_d= X'_q.

• obliczyć admitancje zastępcze odbiorów z zależności:

(64)

gdzie:
- zespolona i sprzężona moc pozorna odbioru, U_L- napięcie odbioru.

• wyeliminować węzły odbiorcze wyznaczając macierz transferową Y_G

Y_G= Y_GG-Y_GLY_LL^-1Y_LG (65)

gdzie: Y_GG- podmacierz admitancyjna odpowiadająca węzłom generatorowym wewnętrznym, Y_LL- podmacierz admitancyjna odpowiadająca węzłom odbiorczym, Y_GL, Y_LG- podmacierze admitancji wzajemnych między węzłami generatorowymi wewnętrznymi i węzłami odbiorczymi sieci.

• zlinearyzować układ równań algebraiczno- różniczkowych wyznaczając macierz stanu A.

• obliczyć wartości własne i wektory własne macierzy stanu oraz przeprowadzić analizę modalną w celu właściwego doboru parametrów układu regulacji generatora.

Dla układu generator- sieć sztywna przedstawionego na rysunku 15 można ułożyć następujący układ nieliniowych równań opisujących stan generatora:

Przed linearyzacją:

• równanie prędkości wirnika:

(66)

• równanie ruchu zespołu turbina- wirnik generatora:

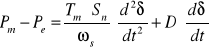
(67)

gdzie :

P_m- moc mechaniczna turbiny,

P_e- moc elektryczna generatora,

T_m - mechaniczna stała czasowa w s,

S_n - moc znamionowa generatora w MW,

ω_s - pulsacja znamionowa w rad/s,

δ - kąt położenia osi q wirnika maszyny względem kierunku odniesienia, za który przyjmuje się kierunek wektora U_s,

D - dodatni współczynnik tłumienia maszyny w MWs/rad

• równanie różniczkowe obwodu wzbudzenia:

(68)

gdzie:

e_q'- sem przejściowa w osi poprzecznej,

X_d- reaktancja synchroniczna podłużna,

X'_d- reaktancja przejściowa podłużna,

T'_do- stała czasowa podłużna biegu jałowego generatora,

i_d- prąd stojana w osi podłużnej,

e_f- sem wzbudzenia

• równanie operatorowe układu regulacji napięcia:

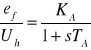
(69)

gdzie:

K_A- współczynnik wzmocnienia,

T_A- stała czasowa,

U_h- sygnał na wejściu regulatora,

K₁÷K₆- stałe wyliczane w oparciu o parametry systemu.

Po linearyzacji i przekształceniach nieliniowego układu równań (66) do (69) otrzymujemy następujący układ liniowych równań różniczkowych:

(70)

(71)

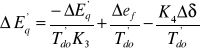
(72)

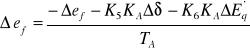
(73)

Wektor zmiennych stanu ma tutaj następującą postać:

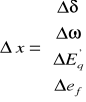
(74)

Na podstawie układu liniowych równań różniczkowych (70) do (73) otrzymujemy macierz stanu opisującą SEE:

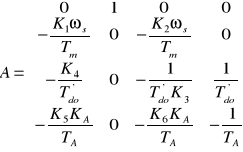
(75)

Z postaci macierzy stanu wynika, że elementy macierzy stanu zależą od punktu pracy systemu w stanie ustalonym oraz od parametrów układów regulacji. Od punktu pracy zależą wartości współczynników K₁÷K₆. Stała czasowa T_m zależy od konstrukcji generatora, natomiast stała czasowa T'_do od rodzaju wzbudnicy. Stała czasowa T_A i współczynnik K_A zależą od typu regulatora napięcia. Po wyznaczeniu wartości własnych i wektorów własnych macierzy stanu można badać wpływ stałych czasowych i współczynników wzmocnienia na stabilność systemu generator- sieć sztywna.

Przykład

Zbadać stabilność lokalną systemu generator- sieć sztywna, pokazanego na rysunku poniżej.

Rys. 29 Schemat układu do przykładu 4.

W wyniku częściowego rozwiązania zadania według metodologii podanej powyżej w punkcie 4 uzyskano następujące dane cząstkowe:

K₁= 0,483,

K₂= 0,543,

K₃= -0,435,

K₄= -2,641,

K₅= -0033,

K₆= 0,442

W temacie zadania podano:

K_A= 10,

T_A= 0,5s,

T_m= 6,45s,

T'_do= 9,2s,

ω_s= 314 rad/s

Do dalszych obliczeń przyjęto postać macierzy stanu podanej we wzorze (75):

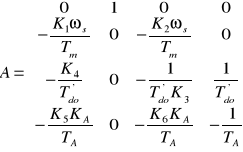
Po podstawieniu danych uzyskano następującą macierz stanu:

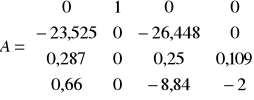
Do prowadzenia dalszych obliczeń użyto programu Mathcad 5.0 Plus. Dzięki temu wyliczono wartości własne macierzy stanu λ_i oraz wektory własne prawostronne m_i. Formuły użyte przy obliczeniach zamieszczono na rysunku poniżej.

Rys. 30 Formuły użyte przy obliczeniach w programie Mathcad.

Jak widać na rysunku 29 wyliczono cztery wartości własne macierzy stanu A:

λ₁= 0,171 + j4,846

λ₂= 0,171 - j4,846

λ₃= -1,046 + j0,312

λ₄= -1,046 - j0,312

Zgodnie z teorią podaną powyżej w punkcie 4.2 odpowiedź systemu na małe wymuszenie jest określona przez wartości własne λ_i i wektory własne macierzy stanu. Zespolone wartości własne leżące w prawej półpłaszczyźnie powodują rosnące oscylacje, w lewej półpłaszczyźnie - malejące oscylacje. Dodatnie części rzeczywiste wartości własnych powodują wykładniczy wzrost wartości zmiennej stanu, a ujemne części - monotoniczne zanikanie. Warunkiem stabilności lokalnej jest wiec, by wszystkie wartości własne macierzy stanu A miały części rzeczywiste ujemne.

W rozpatrywanym zadaniu okazało się, że dwie spośród czterech wartości własnych mają dodatnie części rzeczywiste (λ₁ i λ₂). Oznacza to, że badany układ będzie niestabilny lokalnie i każde małe wymuszenie spowoduje oscylacyjnie narastające zmiany kąta wirnika.

Wykaz literatury:

1. [1] Materiały z wykładów „Praca systemów elektroenergetycznych” prowadzonych przez dr inż. Janusza Brożka,

2. [2] Z. Kremens, M. Sobierajski „Analiza systemów elektroenergetycznych”, WNT Warszawa 1996,

15

---