 | Pobierz cały dokument przygotowanie.do.sprawdzianu.funkcja.doc Rozmiar 447 KB |
PRZYGOTOWANIE DO SPRAWDZIANU - FUNKCJA KWADRATOWA ( I )
POZIOM ROZSZERZONY
DOPUSZCZAJĄCY
1. a) Podaj wzór jednomianu stopnia drugiego, wiedząc, że do jego wykresu należy punkt ![]()
.
b) Sprawdź, czy punkt ![]()
należy do wykresu funkcji ![]()
.
2. a) Podaj postać kanoniczną funkcji kwadratowej, której wykres otrzymamy przesuwając równolegle
wykres jednomianu stopnia drugiego ![]()
o wektor ![]()
.
b) Podaj wzór jednomianu kwadratowego oraz współrzędne wektora, o jaki należy przesunąć
wykres tego jednomianu, aby otrzymać wykres funkcji ![]()
.
3. a) Wyznacz współrzędne wierzchołka paraboli o równaniu 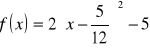
.
b) Oblicz sumę obu współrzędnych wierzchołka paraboli będącej wykresem funkcji kwadratowej
![]()
.
4. a) Odczytaj współczynniki a, b, c funkcji kwadratowej dane w postaci ogólnej ![]()
.
Wiedząc, że ![]()
podaj postać ogólną funkcji kwadratowej.
5. a) Zbadaj, ile miejsc zerowych ma funkcja kwadratowa ![]()
.
b) Na podstawie postaci iloczynowej funkcji kwadratowej ![]()
, podaj jej miejsca
zerowe.
c) Znając współczynnik a oraz miejsce zerowe funkcji kwadratowej, podaj jej
postać iloczynową : ![]()
.
6. Przedstaw w postaci iloczynowej funkcję kwadratową daną w postaci ogólnej ![]()
(o ile to możliwe). Podaj miejsca zerowe funkcji (o ile istnieją).
7. Sprowadź do postaci ogólnej funkcję kwadratową daną w postaci kanonicznej ![]()
.
8. Rozwiąż równania : ![]()
, ![]()
.
9. Rozwiąż nierówności : ![]()
, ![]()
, ![]()
.
10. Naszkicuj wykres funkcji a) ![]()
b) ![]()
c) ![]()
Na jego podstawie omów własności tej funkcji.
DOSTATECZNY
1. Dana jest funkcja w postaci iloczynowej ![]()
.
Wyznacz współrzędne wierzchołka paraboli oraz zbiór wartości funkcji f.
Podaj postać kanoniczną tej funkcji oraz równanie osi symetri wykresu funkcji f.
2. Dana jest funkcja w postaci iloczynowej ![]()
. Podaj jej postać ogólną.
3. Dana jest postać ogólna funkcji kwadratowej ![]()
. Sprowadź ją do postaci
kanonicznej, a następnie do postaci iloczynowej.
4. Wyznacz maksymalny przedział, w którym funkcja kwadratowa ![]()
jest rosnąca.
5. Miejscami zerowymi funkcji kwadratowej ![]()
są liczby 1 oraz ![]()
.
 | Pobierz cały dokument przygotowanie.do.sprawdzianu.funkcja.doc rozmiar 447 KB |