ZAŁOŻENIA PODSTAWOWE: CIĄGŁOŚĆ OŚRODKA I ODKSZTAŁCEŃ:

Założenie o ciągłości ośrodka - jeśli przechodzimy z objętości dużej do objętości nieskończenie małej to medium to zachowuje własności obiektu badanego w dużej objętości

Założenie ciągłości ośrodka pozwala stosować nam rachunek różniczkowy

Założenie ciągłości odkształceń - funkcje które będąc cząstkami, w naszych rozważaniach będą funkcjami ciągłymi

ZMIENNE NIEZALEŻNE: LAGRANGE'A I EULERA, ICH POWIĄZANIA

Zmienna Lagrange'a - jest analizą wędrowną, polega na badaniu właściwości fizycznych( np.: prędkość, gęstość, ciśnienie, temperatura) i opisie poruszającego się płynu. W tej metodzie należy wybrać cząstkę np. poprzez opisanie jej położenia w czasie t₀ otrzymujemy wtedy: x₀, y₀, z₀ a następnie śledzi się dana cząstkę w kolejnych chwilach t. Otrzymujemy w ten sposób opis ruchu płynu w postaci funkcji współrzędnych położenia początkowego i czasu:

= f (x₀, y₀, z_0, t) gdzie
jest współrzędną położenia lub własnością płynu w chwili t.. Współrzędne położenia elementu płynu w kolejnych chwilach czasowych, wyrażające parametryczne równanie toru cząsteczki określają równania:

x =x(x₀,y₀, z_0, t); y= y(x₀, y₀, z_0, t); z = z(x₀,y_0,z_0, t)

Składowe prędkości poszczególnych elementów płynu wynoszą:

V_x = ∂x/∂t; V_y = ∂y/∂t; V_z = ∂z/∂t

a składowe przyspieszenia:

a_x = ∂²x/∂t²; a_y = ∂²y/∂t²; a_z = ∂²z/∂t²

Inne parametry stanu ruchu płynu np. gęstość i ciśnienia, wyraża się zgodnie ze wzorem:

= f (x₀, y₀, z_0, t) a więc:

ρ = ρ (x₀, y₀, z_0, t); p = p (x₀, y₀, z_0, t)

Metoda Eulera - analiza lokalna. Opisuje zmiany wielkości fizycznej płynu z poszczególnych punktów przestrzeni, w której odbywa się ruch. V_x = f (R, t)

V_x = f_x(x, y, z, , t) V_y = f_y(x, y, z, , t) V_z = f_z(x, y, z, , t)

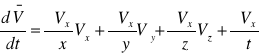
przyśpieszenie cząsteczki wyrażone za pomocą pochodnej substancjalnej

Zależność między L i E:

SIŁY DZIAŁAJĄCE NA PŁYNY - POWIERZCHNIOWE I MASOWE

Wszystkie siły działające na ciało lub jego część można podzielić na dwie grupy: siły masowe i siły powierzchniowe.

Siły masowe -wielkości proporcjonalne do masy ciała i przyczepione do niej (np. siła bezwładności)

-działają na całą masę płynu i są do niej proporcjonalne. Siłami masowymi są: siła bezwładności, ciężar, siła elektromagnetyczna itp. Miara sił masowych jest jednostkowa sił masowa będąca stosunkiem siły masowej do masy, na która działa ta siła:

Jednostkową siłą masową siły ciążenia jest g - przyspieszenie ziemskie, a sił bezwładności - wektor równy przyspieszeniu, ale zwrócony w kierunku przeciwnym niż przyspieszenie.

Siły powierzchniowe - siły działające na powierzchnię zewnętrzną ciała lub wewnętrzną, wydzielone w umowny sposób.

- działają na powierzchnie ograniczające ciało lub wyodrębniona jego część. Siłami powierzchniowymi są: parcie cieczy na ściankę zbiornika, nacisk tłoka, siła wyporu unosząca statki, siły aerodynamiczne działające na samolot itp. Miarą sił powierzchniowych jest jednostkowa siła powierzchniowa czyli stosunek siły powierzchniowej Fp do powierzchni A:

Siły rozkładamy na składowe σu, τ1, τ2

WŁASNOŚCI FIZYCZNE CIECZY

- gęstość - płynu wiąże się z masą danego ośrodka i wyraża się stosunkiem masy m do objętości V, jaką ta masa zajmuje.

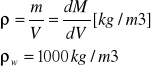
Gęstość jest funkcją temperatury i ciśnienia

- Ciężar właściwy
wyraża się stosunkiem ciężaru ciała do jego objętości

- Objętość właściwa
równa jest odwrotności gęstości

- Ściśliwość płynu - zdolność płynu do zmiany objętości w danej temperaturze przy zmianie ciśnienia. Jego miarą jest współczynnik ściśliwości

- który określa względną zmianę objętości płynu przypadającą na jednostkę przyrostu ciśnienia dla stałej temperatury ośrodka

- Moduł sprężystości objętościowej wyraża się odwrotnością współczynnika ściśliwości

0^oC 1,95 GPa

10^oC 2,05 GPa

- Rozszerzalność cieplna - jest zdolnością płynu do zmiany swej objętości przy danym ciśnieniu pod wpływem zmian temperatury. Własność tę opisuje współczynnik rozszerzalności cieplnej(wyraża względną zmianę objętości przypadającą na jednostkę przyrosty temperatury w danym ciśnieniu)

- Lepkość - własność płynu objawiając a się tym, że przy przesuwaniu się warstw cieczy pojawia się siła tarcia:

μ [Ns/m2] - dynamiczny współczynnik lepkości

ν [m2/s] - kinematyczny współczynnik lepkości

Lepkość cieczy zależy od p i T. Im temperatura wyższa, tym lepkość mniejsza. Ciśnienie na lepkość ma niewielki wpływ.

-Napięcie powierzchniowe - spójność - zjawisko występujące na granicy 2 różnych ośrodków. Jeśli cząstka jest otoczona takimi samymi sąsiadami ze wszystkich stron to siły=0. Gdy cząsteczki są różne - to ciśnienie w środku kropli wody jest trochę większe wewnątrz niż na zewnątrz.

Czym większe zakrzywienie kropli, tym większy jest efekt oddzielania kropli. Na powierzchni rozdzielającej 2 ośrodki istnieje błona powierzchniowa, w której istnieje napięcie powierzchniowe.

- Kapilarność - zjawisko podsiąkania

- Dyfuzja molekularna - gdy są 2 mieszaniny, to na skutek zjawiska dojdzie do zmieszania. Miara tego zjawiska jest współczynnik dyfuzji molekularnej

D[m2/s],
, gdzie dC -różnica koncentracji, dl - odległość między 2 punktami, I - ilość substancji jaka ulega przeniesieniu.

- Ciepła:

- ciepło właściwe - ilość ciepła jaką trzeba dostarczyć, aby temperatura wzrosła o 1cal/g, cw =4,1868kJ/kgK

- ciepło topnienia - ilość ciepła jaką trzeba dostarczyć do jednostki masy, aby 1 kg lodu przeprowadzić w stan wody, ct=333kJ/kgK

- ciepło parowania - ciepło jakie trzeba dostarczyć do jednostki masy aby 1 kg wody przeprowadzić w stan lotny, cp=2257kJ/kgK

OGÓLNE SFORMUŁOWANIA ZADAŃ MECHANIKI PŁYNÓW

W danym obszarze wypełnionym płynem o własnościach scharakteryzowany prze współczynniki α (rozszerzalność cieplną), β (ściśliwość) ściśliwość (lepkość) zależnych od temp i ciśnienia, na płyn działa pole sił masowych F_mj(x,y,z,t), a na granicach obszaru oddziałują siły powierzchniowe - normalne i styczne. Granice obszaru mogą być nieprzenikliwe dla płynu - nieruchome i ruchome, albo mogą to być powierzchniowe umowne, przez które przenika płyn. W tym przypadku musi być zadana na granicy prędkość lub ciśnienie płynu.

Zadanie jest rozwiązane, gdy w każdym punkcie obszaru (x,y,z) i w każdej chwili t, są znane: prędkość v, ciśnienie p, gęstość ρ i temperatura T.

Zadanie zostało sformułowane w zmiennych niezależnych Eulera (x,y,z,t). Funkcjami poszukiwanymi są wektor v i skalary p, ρ, T. Do rozwiązani potrzebujemy 4 równań są to podstawowe równania mechaniki wyrażające: zasadę zachowania masy (skalarne), zasadę zachowania pędu (wektorowe), zasadę zachowania energii (skalarne), równanie stanu (skalarne).

Jeżeli wydzielić z rozważań zagadnienia termodynamiczne, pomijamy T, ale musimy w tym przypadku pominąć równanie zachowania energii, obejmuje ono bowiem bilans wszystkich rodzajów energii, a więc również i ciepła. Gdy płyn jest nieściśliwy, równanie stanu sprowadza się do warunku ρ = const.

POSZUKIWANE FUNKCJE (POLA) V, P, Ρ, T I PODSTAWOWE PRAWA ŁĄCZĄCE NIEWIADOME: PRAWA ZACHOWANIA MASY, PĘDU, ENERGII, RÓWNANIE STANU

Zasada zachowania masy: stosowana w postaci równania ciągłości przepływu

1 - zmiana masy w obszarze V uwarunkowana zmianą gęstości płynu w czasie dt

2 - masa płynu , która w tym samym czasie popłynęło przez powierzchnie A, różnica masy wpływającej i wypływającej z ośrodka

dAwektor- wektor o wartości równej polu dA , normalnym do tej powierzchni i skierowany na zewnątrz obszaru

W objętości kontrolnej, zmiana masy w ośrodku równa jest masie doprowadzanej lub odprowadzanej z ośrodka.

Zasada zachowania pędu: z zasady zachowania pędu wynika, że zmiana pędu pewnej masy jest równa popędowi sił działających na tą masę. Równanie opisujące tę zasadę nazywamy równaniem ruchu.

1-zmiana pędu

2-popęd sił masowych

3-popęd sił powierzchniowych

Suma wszystkich sił plus siła bezwładności jest =zeru.

Zasada zachowania energii

Energia kinetyczna zmienia się w wyniku pracy wykonanej przez siły masowe i powierzchniowe

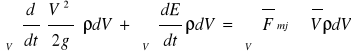
1- zmiana energii kinetycznej w czasie

2 -energia wewnętrzna przypadająca na jednostkę masy płynu

3- praca sił masowych dla całego obszaru

4- praca sił powierzchniowych

Jednostajny strumień ciepła, ciepło

-praca sił skalarnych = wykonana praca

Równanie zachowania energii mechanicznej

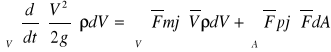
Energia kinetyczna zmienia się w pracy wykonanej przez siły masowe i powierzchniowe

Równanie zachowania(bilansowe) ciepła

Równanie stanu:

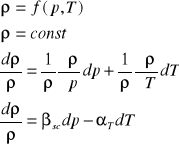
alfa - wsp rozszerzalności (zmienny)

beta - wsp ściśliwości (w miarę stały)

Najprostszą postacią równania stanu, bardzo często używaną w praktyce jest ρ=const. przy założeniach że płyn jest nieściśliwy ( albo jego ciśnienie jest stałe) i pozbawiony rozszerzalności cieplnej (albo że jego temperatura jest stała).

RODZAJE PÓL PRĘDKOŚCI, LINIA PRĄDU, TOR, SMUGA, RURKA PRĄDU, STRUMIEŃ

Linia prądu - linia pola wektorowego definiowana dla pewnej chwili. W każdym miejscu jest styczna do wektora prędkości w tym miejscu

Tor - linia zakreślona w przestrzeni przez poruszającą się cząstkę

Smuga - miejsce geometryczne cząstek, które przeszły przez określony punkt w przestrzeni

Rurka prądu - zbiór linii prądu, które przeszły przez zamknięty obwód

Struga - pęk linii prądu, które przeszły przez nieskończenie małą powierzchnię

Strumień - pęk linii prądu, które przeszły przez skończoną powierzchnię (pole o skośnej powierzchni)

ODKSZTAŁCENIE CZĄSTKI CIECZY, DIVERGENCJA, ROTACJA, SZYBKOŚĆ ŚCINANIA

Wzory Helmholtza:

Vx= Vxo +∂Vx/∂x ξ +∂Vx/∂y η+ ∂Vx/∂z ζ

Vy= Vyo +∂Vy/∂x ξ +∂Vy/∂y η+ ∂Vy/∂z ζ

Vz= Vzo +∂Vz/∂x ξ +∂Vz/∂y η+ ∂Vz/∂z ζ

przemieszczenie obrót zmiana czasu

∂Vx/∂z ζ+ ∂Vy/∂z ζ- deformacja

∂Vx/∂z ζ- ∂Vy/∂z ζ- obrót

Co to znaczy ∂Vx/∂x, ∂Vy/∂y , ∂Vz/∂z

założenia: V_z= 0, ∂ /∂_z =0, ∂Vy/∂x= 0, ∂Vx/∂y =0

∂Vx/∂x - zmiana prędkości w kierunku ruchu, droga jaką przebyła cząsteczka względem P(0,0)

AA'=∂Vx/∂x* ξ*dt +∂, BB'=∂Vy/∂y*η*dt. Cząsteczka nie przemieściła się, lecz zmieniła swoje wymiary, nie zmieniła kształtu

Prędkość wydłużenia względnego

εx = ∂Vx/∂x, εy = ∂Vy/∂y, εz = ∂Vz/∂z

Szybkość wydłużenie względnego = wydłużenie względne/czas

Wydłużenie względne = wydłużenie/ wartość początkowa

Względna prędkość objętości:

∂Vx/∂x ξ+∂Vy/∂y η+∂Vz/∂z ζ

Względna szybkość zmiany przyrostu objętości:

∂Vx/∂x +∂Vy/∂y +∂Vz/∂z =div V(wektor) = F

Jeżeli div V jest ujemne to cząstka zmniejsza swoją objętość

Co to znaczy ∂Vx/∂y, ∂Vy/∂x

założenia: Vz=0, ∂ /∂z= 0 , ∂Vx/∂x=0, ∂Vy/∂y=0

AA'=∂Vy/∂x *ξ*dt , BB'=∂Vx/∂y*η*dt. Przekątna cząstki zmieniła krawędź, cząstka uległa obróceniu.

dβ=(dα1- dα2)/2=dt(∂Vy/∂x+ ∂Vx/∂y)/2

Prędkość kątowa obrotu cząstki dookoła osi z

ωz=(∂Vy/∂x - ∂Vx/∂y)/2= Ωz*1/2= 1/2*(rot V wektor)_z

(rot V wektor_)z - wektor rotacji

Ωz - szybkość z jaka przesuwają się boki po przekątnych

Szybkość, z jaka przesuwają się boki do osi cząsteczki

θ z= (dα1+ dα2)/ (2dt) - szybkość kątowa dwóch ścianek względem siebie

1/2θ z= (∂Vy/∂x+ ∂Vx/∂y)/2

θ z+Ωz=∂Vy/∂x-∂Vx/∂y+∂Vy/∂x+∂Vx/∂y

∂Vy/∂x=1/2(θ z+Ωz) deformacja kątowa

∂Vx/∂y= 1/2(θ z-Ωz) szybkość obrotu

Rotacja (wirowość) - operator różniczkowy działający na pole wektoroweF, tworzy pole wektorowe wskazujące wirowanie (gęstość cyrkulacji) pola wyjściowego. Oznaczana jest przez rot lub curl (z ang. rotacja), czasami również zapisywana jako dF.

Jeżeli rotacja danego pola wektorowego jest równa zero (wektorem zerowym), to pole to jest bezwirowe. Pole bezwirowe posiada potencjał (i odwrotnie: pole posiadające potencjał jest polem bezwirowym).

Rotację definiuje się jako iloczyn wektorowy operatora nabla▼ i wektora F:

.

W kartezjańskim układzie współrzędnych F = [F_x,F_y,F_z] mamy więc

.

Dywergencja jest operatorem różniczkowym, który danemu polu wektorowemu przypisuje pole skalarne. Jeżeli polem wektorowym jest pole prędkości płynięcia nieściśliwego płynu, to dywergencja większa od zera oznacza, że w tym punkcie do układu ciecz dopływa (tu jest jej źródło), jeśli zaś mniejsza od zera, to tu następuje jej odpływ (ma tu swoje ujście). Gdy dywergencja jest równa zeru, to w danym punkcie nie ma ani dopływu, ani odpływu albo oba są sobie równe.

W przypadku pola elektrycznego takimi "źródłami" pola są ładunki, dlatego dywergencja pola elektrycznego jest proporcjonalna do gęstości ładunku w danym punkcie przestrzeni (różniczkowe prawo Gaussa).

Pole wektorowe o zerowej dywergencji nazywamy bezźródłowym. Przykładem takiego pola jest pole magnetyczne (brak monopoli magnetycznych — w przyrodzie obserwuje się wyłącznie dipole).

Definicja

Funkcję: A:R³ R³

Będziemy nazywać polem wektorowym w przestrzeni trójwymiarowej. Dalej będziemy zakładać że powyższa funkcja jest różniczkowalna w całej swej dziedzinie. (dzięki temu mamy pewność o istnieniu pochodnych cząstkowych).

Dywergencja pola wektorowego A jest skalarnym operatorem różniczkowym, określonym następującą formułą:

Gdzie
jest obszarem w przestrzeni,
brzegiem tego obszaru (czyli pewną powierzchnią zamkniętą), a |S| oznacza pole powierzchni S.

Całka podwójna występująca w definicji nosi nazwę strumienia pola wektorowego A po powierzchni S.

W przypadku gdy pole wektorowe określamy korzystając z kartezjańskiego układu współrzędnych można zdefiniować operator wektorowo-różniczkowy zwany operatorem nabla:

gdzie
są to pola wektorowe, zwane wersorami układu współrzędnych kartezjańskich, określone w następujący sposób:

Co zapisuje się jako formalny iloczyn skalarny operatora nabla i pola A

Szybkość ścinania (prędkość odkształcenia postaciowego) jest pochodną odkształcenia postaciowego według czasu. Można ją także zdefiniować jako zależność zmiany prędkości od położenia:

Przy czym zamiast x i z można użyć dwóch dowolnych, różnych indeksów.

RODZAJE RUCHU: USTALONY - NIEUSTALONY, JEDNOSTAJNY - NIEJEDNOSTAJNY, 3D-2D-1D, POTENCJALNY - WIROWY

**Ruch nieustalony: ∂f (x,y,z,t) / ∂t różne od 0

**Ruch ustalony (stacjonarnrny): pole, k nie zalezy od czasu ∂f/∂t = 0

**Ruch jednostajny: wartość prędk w tym ruchu jest stała. Pr średnia = pr chwilowej. v = const v=Δn/ Δt ΔN=N₂-N₁ Δt=t₂-t₁

**Ruch niejednostajny to ruch podczas którego prędkość ciała zmienia swoją wartość w miarę upływu czasu.

Pole ustalone - pole wektorowe prędkości opisane funkcją v = F (x,y,z,t), które jest niezmienne w czasie tzn. ∂v/∂t = 0

Pole wirowe - pole wektorowe prędkości kątowej chwilowego obrotu ω. Wektor prędkości kątowej chwilowego obrotu jest ≠ 0

Pole potencjalne - to takie, dla którego ilość energii konieczna do przemieszczenia ciała z jednego punktu do drugiego nie zależy od drogi. Pole potencjalne jest zwykłe opisane poprzez wektor siły określony dla każdego punktu przez funkcję wektorową. Rotacja pola potencjalnego jest równa zero.

Funkcja V(-) = f(x,y,z,t) opisuje pole wektora prędkości. Jeżeli pole to jest niezmienne w czasie, czyli (dv/dt=0) ruch nazywamy ustalonym (pole jest stacjonarne). W przypadku, gdy nie ma przyspieszeń dv/dt = 0 każda cząstka porusza się ruchem prostoliniowym ze stałą prędkością - ruch jest jednostajny. Wreszcie, gdy V(-) = const pole jest jednorodne i ruch odbywa się bez wzajemnych przesunięć cząstek.

Jeżeli istnieje układ współrzędnych geometrycznych Eulera (prostokątny, walcowy, sferyczny a nawet krzywoliniowy) taki, ze składowe prędkości oraz pochodne wszystkich zmiennych w kierunku jednej osi są zerowe - to pole prędkości i ruch są dwuwymiarowe. Jeżeli jest to układ prostokątny to ruch nazywamy płaskim. Gdy istnieją dwie zmienne o podanej własności - ruch jest jednowymiarowy

Pola dwuwymiarowe znajdują częste zastosowanie jako wystarczająco dobre przybliżenie opisu ruchu bardziej złożonego, jeżeli badany obiekt jest długi w jednym kierunku np. przepływ przez przelew, przesiąkanie przez groble. Przepływy ściśle jednowymiarowe występują rzadko w naturze.

WŁASNOŚCI RUCHU POTENCJALNEGO I WIROWEGO

Ruch potencjalny i wirowy:

Wektor wiru jest definiowany w postaci: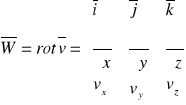
, a jego składowe wynoszą:

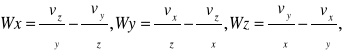
Ruch w którym W=rotv=0 nazywamy ruchem potencjalnym

Ponieważ W=2ω, to z tego faktu wynika ze w ruchu potencjalnym cząski płynu nie wykonują obrotów wokół własnej osi

W ruchu potencjalnym istnieje funkcja skalarna Ф(x,y,z), której pochodne cząstkowe są składowymi wektora prędkości:

Czyli gradФ=v

Całkowita zmiana potencjału 2 sąsiednich cząstek plynu wynosi:

Równanie dФ=0, czyli Ф=const, które można zapisać w postaci:

jest równaniem jednakowego potencjału

RÓWNANIE RÓŻNICZKOWE CIĄGŁOŚCI I JEGO PRZYPADKI SZCZEGÓLNE

Równanie ciaglosci

Dla plynu niescisliwego(
) divv=0 (czasteczka nie moze zmieniac objetosci a jedynie ksztalt)

RÓWNANIE NAVIERA - STOKESA:

Równanie analizy ruchu płynu lepkiego w postaci wektorowej:

dV /dt = F_mj - 1/ρ gradp + ν ∇²V + ν/3*grad* divV

1 - siła bezwładności ruchu płynu

2 - działanie sił masowych;

3 - różnica sił normalnych, działanie sił powierzchniowych normalnych

4 - siła tarcia stycznego, szybkość poślizgu;

2,3,4 - efekt sił tarcia;

5- dodatkowe siły tarcia związane ze zmianą objętości cząstki, siły tarcia styczne związane ze zniekształcaniem się płynu ściśliwego

a) Założenia,

Założenia ograniczają się do ciągłości ośrodka i ciągłości odkształceń oraz przyjęcia warunków, że naprężenia styczne są proporcjonalne do szybkości odkształceń kątowych cząstki.

Równanie dotyczy płynów sprężystych i lepkich- newtonowskich, pole prędkości ciągłe i różniczkowalne.

b) tensor naprężeń (9 niewiadomych naprężeń),

„+”jeżeli naprężenie bez ` zgodne z osią

„-„jeżeli naprężenie z primem ` przeciwnie niż oś.

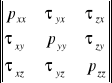
-tensor naprężeń

(macierz naprężeń)

→-kierunek ,↓-na ścianke

c) sposób ich redukcji,

Równanie pędu w rzucie na oś x.

????Zmiana pęd =suma sił (masowych i powierzchn)

Zerowały się wielkości małe rzędu drugiego????

d) ogólna definicja ciśnienia - przypadki szczególne

Def; ↑ ciśnienie -jest to średnia 3 naprężeń normalnych działających na cząstkę

!! ,stąd:

!!

Co się będzie działo?

1) płyn nielekki µ=0 Napręż. normalne są takie same

2) prędkość prędkość = const p_xx = p Ciśnienie utożsamia się z napr. normal. wtedy gdy płyn jest nieruchomy lub nielekki,

stąd wzór Naviera-Stoksa

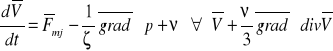
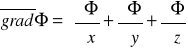
-def. gradientu

e) analiza równania Naviera - Stokesa (co reprezentują kolejne wyrazy, przypadki szczególne),możliwości rozwiązania

Przypadki szczególne (modyfikacje N-S)

(-przed oznacza wektor):

1)płyn nieściśliwy (=const => div(-)υ = 0)

d(-)υ/dt = (-)F_mj-1/ρ gradp+mi∇²V(-)

2)płyn nie lepki (mi=0)

d(-)υ/dt = (-)F_mj-1/ρ gradp - równanie Eulera

3)płyn we względnym bezruchu tzn istnieje taki układ odniesienia (który sam może być ruchomy) względem którego v(-)=0

(brak ruchu względnego) dv/dt = 0

0 = (-)F_mj-1/ρ gradp - równanie statyki

Modyfikacja

d(-)υ/dt = (-)F_mj-1/ρ gradp N-S mówi o tym ze gdy płyn jest nielekki to stosowane jest równanie zmodyfikowane

Założenia: 1) mi=0 , 2) ruch ustalony , 3) płyn barotropowy ro=f(p) , Fmj = grad - siły masowe powodują potencja

RÓWNANIE RÓŻNICZKOWE DLA CIECZY NIELEPKICH I JEGO CAŁKI

Równanie Eulera:

Założenia: płyn jest nie lepki ν = 0

dv/dt - siły bezwładności

F_mj - siły masowe jednostkowe

1/ρ grad p - siły powierzchniowe normalne

RÓWNANIE BERNOULIEGO I RÓWNANIE CAUCHY'EGO - ZAŁOŻENIA I WYNIK CAŁKOWANIA

Całka Bernoulliego

Założenia: ruch ustalony, siły masowe mają potencjał, płyn jest barotropowy (gęstość jest funkcją zależną tylko od ciśnienia).

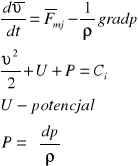
Ci - stała dla danego toru (linii prądu)

Całka Cauchy'ego

Założenia: ruch bezwirowy, ciecz barotropowa.

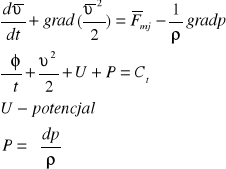
ISTOTA TURBULENCJI, DOŚWIADCZENIE I LICZBA REYNOLDSA

Turbulencja

W pewnym zakresie prędkości pojawiają się zaburzenia. Przyprzepływie mamy działania w 2 kierunkach bezwladnosci. Powstają pobudzenia cząstek do ruchów chaotycznych. Im mniejszy przekrój tym geomeria bardzij stabilna i siły czasteczkowe wieksze.

Opory ruchu przy przepływach są proporcjonalne do kwadratu prędkości.

Rodzaj ruchu zależy od prędkości i liczby Reynoldsa
W strefie przejściowej po jednokrotnym wzburzeniu ruchu laminarnego nie ma juz powrotu.

Re<2320 ruch laminarny

Re>4000 ruch turbulentny

dla ruchu ustalonego(prędkość stała w czasie):

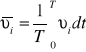
dla ruchu nieustalonego:

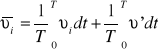
zakladamy, ze turbulencja jest izotropowa (jednakowa we wszystkich kierunkach)

Równanie Reynoldsa

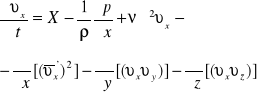
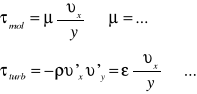
DOŚWIADCZENIE REYNOLDSA - polegało na obserwacji zachowania się zabarwionej strugi cieczy (smugi) w strumieniu płynącym ruchem jednostajnym szklaną rurą. Przy bardzo małych prędkościach barwnik układał się w cienką strugę, przy przekroczeniu pewnych prędkości obraz gwałtownie się zmieniał. Zabarwiona struga pulsowała, rozpływała się i w końcu zaczęła zanikać. Oznacza to, że oprócz przesunięć w kierunku zasadniczym wystąpiły dodatkowe ruchy poprzeczne powodujące wymianę cząstek między poszczególnymi strugami i zmieszanie cieczy.

Re = v d ρ/μ = v d / ν

- Re ≤ 2320 ruch laminarny

- Re > 4000 ruch turbulentny

- Re = 50000 max osiągnięta wartość Re.

WARTOŚCI: PRZECIĘTNA I PULSACJA PARAMETRÓW RUCHU, INTENSYWNOŚĆ TURBULENCJI, TURBULENCJA IZOTROPOWA

Ruch turbulentny - duża wartość Re, energia przekazywana z ruchu podstawowego do pulsacyjnego jest większa niż ciepło wytworzone na skutek tarcia. W efekcie przepływ traci stateczność, zaburzenia wzmagają się i rozprzestrzeniają się.

Wartość przeciętna prędkości:

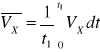
Wartość przeciętna:

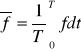
Dla ustalonych warunków brzegowych pole parametrów jest stałe.

Pulsacja:

z def: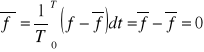

Przeciętna wartość pulsacji jest równa zero.

Intensywność turbulencji:

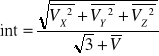
Drgania niewielkie, ale bardzo szybkie.

Turbulencja izotropowa:

Niezależna od kierunku.

RÓWNANIA REYNOLDSA: ZAŁOŻENIA, ISTOTA WPROWADZANIA, ANALIZA RÓWNANIA, NAPRĘŻENIA TURBULENTNE I LEPKOŚĆ TURBULENTNA

Równanie ruchu Reynoldsa

Jest to równanie Reynoldsa dla składowej x, dotyczącego przepływów turbulentnych.

Dla ruchu turbulentnego oprócz tarcia wynikającego z lepkości pojawia się tarcie turbulentne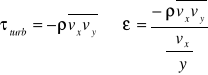

gdzie(-ρ) odpowiada za turbulentne naprężenia styczne.

Ε - współczynnik lepkości burzliwej turbulentnej

Naprężenie to działa na powierzchni xy, więc jest prostopadłe do osi z.

TEORIA PRANDTLA: ZAŁOŻENIA, WNIOSKI

Założenia teorii Prandtla.

Przepływ płynu charakteryzuje się dużymi wartościami liczby Re, siły lepkości nie odgrywają istotnych zmian i można je pominąć. Ze wzrostem Re przepływ przybiera charakter płynu nielepkiego.

Założenia:

- ruch płaski, nie ma prędkości w trzecim kierunku oraz zmian prędkości

- prędkości w kierunku x są dużo większe od prędkości w kierunku y.

- zmiany czegokolwiek w kierunku y są o wiele większe niż w kierunku x.

Teoria ta określa związek między naprężeniami τ turbulentnymi a prędkością uśrednioną.

W strefie laminarnej - τ_{L >} τ_T

W strefie przejściowej - τ_{L =} τ_T

W strefie turbulentnej - τ_{L <} τ_T

gdzie Vx i Vy to uśrednione prędkości w kierunku odpowiednich osi

Teoria Prandtla mówi o związku pomiędzy naprężeniami turbulentnymi a prędkością uśrednioną

Wzór na przeciętną wartość prędkości:

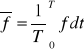
dla teorii Prandtla

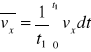
Naprężenia styczne turbulentne

w teorii Prandtla

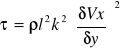
TEORIA KOŁMOGOROWA, RÓŻNE MODELE TURBULENCJI

Hipoteza Kołmogorowa

Opisuje ruch turbulentny- w ruchu tym mamy do czynienia z wirami. Turbulencja jest strukturą wirową-najpierw jest wir duży.czym mniejszy wir tym większy jest gradient prędkości.Duże wiry napędzają wiry średnie i małe.

Skala wirów: l - skala wirów 1°- największych ; η - skala wirów dyssypacyjnych ( ich energia zanika=;

Ruch turbulentny jest ruchem wirowym. Tworzenie się wirów w ruch turbulentnym wynika z tendencji łącznego poruszania się elementów płynu. Na istnienie ciągłej struktury skal wirów w ruchu turbulentnym zwrócił uwagę Kołmogorow wiry powstające podczas przepływu turbulentnego mają różne skale wiry największe odpowiadają rozmiarą kanału w którym odbywa się ruch. Rozmiary wirów najmniejszych są rzędu 1mm i zależą od prędkości średniej przepływu oraz lepkości płynu. Ponieważ rozmiary wirów są wielokrotnie większe od średniej drogi swobodnej l₀ cząsteczek płynu, więc mogą być one traktowane jako ośrodek ciągły. Duże wiry w trakcie przepływu rozpadają się na coraz mniejsze. Na podstawie modelu turbulencji można wyodrębnić 3 skale o wymiarach liniowych

- l skala dużych wirów nazywana też skalą zewnętrzenje turbulencji

- η sprawność, skala wirów małych, ulegających dyssypacji

- l₀ skala molekularna

Turbulencje wg Kołmogorowa można określić jako proces przenoszenia energii kinetycznej od ruchu głównego przez duże wiry do poziomów wirów rozpraszających się. Ponieważ pomija się akumulację energii w wirach o skali pośredniej proces rozpraszania energii turbulencji może być określony na poziomie tworzenia się wirów o największej skali l. Stosunek skali długości l wirów przenoszących energie przepływu do skali długości η wirów, które energie rozpraszają jest proporcjonalny do Re_l^3/4 , Re=υl/v, υ- prędkość średnia ruchu głównego

ZASADA PODOBIEŃSTWA GEOMETRYCZNEGO, KINEMATYCZNEGO I DYNAMICZNEGO

Podobieństwo geometryczne: jest spełnione kiedy kształty oraz wymiary dwóch figur są podobne (np.stosunki boków w trójkątach są takie same). Jako skalę podobieństwa przyjmuje się stosunek dwóch charakterystycznych wymiarów liniowych (np. średnic).

Podobieństwo kinematyczne (pól fizycznych): jest spełnione kiedy pola fizyczne (rozkład linii tych pól) są geometrycznie podobne (np. rozkład linii ciśnienia lub prędkości). Jako skalę podobieństwa przyjmuje się stosunek dwóch wielkości charakterystycznych.

Podobieństwo dynamiczne: jest spełnione kiedy skale podobieństw różnych wielkości charakterystycznych pozostają w ściśle określonych zależnościach (zwanych modułami bezwymiarowymi, np. liczba Reynoldsa dla przepływów). Zależności te uzyskuje się na drodze analizy wymiarowej.

KRYTERIA PODOBIEŃSTWA: RE, FR, CA, WE

LICZBY PODOBIEŃSTWA

- liczba Frouda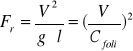

- licz. Reynoldsa

- licz. Cauchy'ego

- licz. Webera
, używając tych liczb redukujemy liczbę doświadczeń

ANALIZA WYMIAROWA, ZASADY BADAŃ MODELOWYCH W MECHANICE PŁYNÓW

Analiza wymiarowa

- aksionat - poprawne równanie musi być zgodne wymiarowo (zgodne jednostki)

- równanie można napisać w postaci bezwymiarowej

Zasady badań modelowych

pytanie→ rozwiązanie

↓_modelowanie ↑_{interpretacja}

model → wynik

_{doświadczenie}

1.modelowanie (zasady)

- schematyzacja- nie wszystko odtwarzamy, decyduje który parametr jest istotny

- wybór kryteriów podobieństwa ( te które chcemy zachować)

-ustalenie wielkości podobieństwa, model duży jest lepszy, pewniejszy, ale wymaga dużo miejsca i jest drogi, zastanawiamy o ile możemy go zmniejszyć aby badania miały sens

- dobór technik pomiarowych

- projekt i budowa modelu

2.doświadczenia

- testowanie i weryfikacja modelu

- właściwe badania

3.interpretacja

- analiza wyników i ocena wpływu uproszczeń

- obliczenie wielkości rzeczywistych

Co jest potrzebne, aby zmienić szybkość obracania się jakiegoś ciała ?

Musi być tarcie

Sposób zmiany rotacji - zadziałać siłą styczną

- zadziałać polem masowym, musi być to pole wirowe( pole sił ciężkości nie jest polem wirowym ) wodzie nie możemy nadać ruchu wirowego tym sposobem

---