REAKCJE WE WNĘTRZU SŁOŃCA
-SYNTEZA TERMOJĄDROWA
We wnętrzu słońca zachodzi cykl p-p
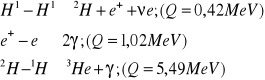
1012kg/s -szybkość powstawania 2H
3He+3He4He+1H+1H (Q=12,8MeV)
+Q=26,7MeV. 5*109 lat wystarczy paliwa na słońcu
Brak
1.Duża gęstość cząsteczek uczestniczących w syntezie -, np. atomy deuteru ulegają jonizacji i tworzy się plazma złożona z deuteru i elektronów.
2. plazma musi być gorąca- wytworzona w laboratorium stan o en.35 keV =(30k więcej niż na słońcu)
3.czas otrzymania plazmy -τ musi być długi
nτ>1020s/m2 -kryterium LAWSONA
inne reakcje syntezy:
D+D3He+n Q=3,27MeV; D+DT+p Q=4,03MeV; D+T4He+n Q=17,6MeV
D+3He4He+p Q=18,4MeV
TOKAMAKI: Utrzymanie plazmy -tokamaki - w kształcie torusa, za pomocą przemian magnetycznej utrzymuje się plazmę tak aby nie stykała się ze ścianami ;- sposób inercyjny - rozgrzewanie i kompresja bardzo małych kuleczek mieszaniny deuteru z trytem przy użyciu laserów lub cząstek o dużej energii z akceleratorów.
FIZYKA CZASTEK ELEMENTARNYCH
460-370p.n.e Demokryt (atom niepodzielny)
Rutherford 10-10m rozmiary atomu, 10-14m rozmiary jądra atomu, 10-15m rozmiary protonów, 10-18m rozmiary kwarków, elektronów
CZĄSTKI:1)Budulec materii (kwarki: u-up, d-down c-chorm, s-stronge, t-top, b-botton) (leptony:elektron, neutrino, mion, neutrino mionowe, taon, neutrino taonowe gdzie mion i taon są cząstkami niestabilnymi - ulegają rozpadowi do elektronu) 2)pośredniczące-przenoszące oddziaływanie (fotony, bozony, gluony, grawitony) Hipotezę kwarków podali w 1964r M. Gell-Mann i H. Zweig.
KLASYFIKACJE CZĄSTEK
I.Ze względu na spin a) spin połówkowy 1/2h,3/2h (fermiony -podlegają statystyce Fermiego-Diraca), b)spin całkowity 0h, 1h (bozony- podlegają statystyce Bozego-Einstaeina)
Cząstki są nierozróżnialne!!!!
[F-cja falowa]2- miara prawdopodobieństwa, że cząstka znajduje się w elementach objętości; [Ψ]2 -nie zależy od tego w której przegrodzie jest cząstka. Wyżej wymienione własności posiadają dwie kombinacje f-cji falowej. 1) Ψi(ri) Ψk(rk) …Ψn(rn) - funkcja symetryczna dla bozonów 2) Ψ1(r1) Ψ1(r2) …Ψ1(rn)
Ψn(r1) Ψn(r2) …Ψn(r2)
-f-cja antysymetryczna dla fermionów
II.Ze względu na oddziaływanie których cząsteczki uczestniczą: a)oddziaływanie silnych HADRONY: 1.Bariony:złożone z 3 kwarków np. proton, neutron (p(uud), n(udd) u=+2/3e,d=-1/3e Bariony są fermionami, Mezo0ny są bozonami 2. Hezony układ kwark-antykwark np. Π -(u-,d) b) w oddziaływaniach słabych LEPTONY elektronymiony, taony oraz ich neutrina.
W 1982 Dirac przewidział że elektron ma swój odpowiednik o takiej samej masie i spinie ale o przeciwnym ładunku elektrycznym. W 1932 odkryto doświadczalnie taką cząstkę pozyton. Obecnie sądzi się że każdej cząstce odpowiada antycząstka (różniąca się znakiem ładunku elektrycznego)
LICZBY KWANTOWE CZĄSTEK ELEMENTARNYCH
Każda cząstka posiada zespół liczb kwantowych którą wyznaczamy doświadczalnie są to wielkości:
1.masa spoczynkowa : mo= 0 dla fotonów, 0-106MeV dla leptonów, 135-880 - mezonów, >938 barionów. 2. Ładunek elek. Cząstki są obojętne lub posiadają ładunek elementarny e dodatni lub ujemny kwarki posiadają ułamkowy ładunek lek. 3.spin i moment magnetyczny μ=-e/m S. 4.statystyka: cząstki są fermionami lub bozonami. 5.liczba barionowa =B i liczba leptonowa =L , bariony mają B=+1, antyboriony -B=-1, Leptony mają L=1 i antyleptony -L=-1
Zasada zachowania liczby barionowej, Zasada zachowania liczby peptonowej. Np.
μ+e++γe+γμ ,Lμ=-1 0 0 , Lμ=-1. 6.Dziwność -S Π++pK++Σ+ tu dla sigma zawsze powstają parami.
ODDZIAŁYWANIA W PRZYRODZIE
a) grawitacyjne μ m grawiton; b)elektromagnetyczne + - foton; c) silne kwark kwark - gluon d) przy rozpadzie cząsteczek pierwiastków -bozony W,Z
ŚCIEŻKA OŚMIOKROTNA
-bariony o spinie 1/2ħ -mezony o spinie 0 ħ
AKCELERATORY-urz.do przyspieszenia. 1. Generator Cockrofta-Waltera 1932r reakcja jądrowa bombardowanie protonami wodór liten
11H+73Li42He+42He, energia cząstek α=8,5MeV, Kp=0,15MeV, Q-Kp=17,2MeV, Kα=8,6MeV 2.Generator Van de Graffa Princeton, napięcie przyspieszające do energi 1-20MeV 3.Cyklotron Lowrence'a Livingstona : pole wytwarzane -kilka T siła Lorenza K=1/2 q2/m2B2r2max - energia max przyspieszanych cząsteczek Cyklotron w Illinois ~200GeV 4.Betatrom Kersta 1941 do przyspieszania elektronów, do rozpędzania elektronów po orbicie kołowej stosuje się pole indukcyjne , elektron przyspiesza się do energii ~100MeV, liczba okrążeń 2,4*105. Współczesne akcelerometry wykorzystuje się do badania wewnętrznej struktury atomów i jąder atomów. Każda cząstka jest falą o długości α=h/Mv, im większy pęd cząstki tym krótsza fala , cząstka =sondą penetrującą materię.
AKCELERATORY LINIOWE: przyspieszenie wywołuje się falą elektromagnetyczną która uderza w grupę cząstek i je unosi.
AKCELERATORY KOŁOWE: kołowe cząstki utrzymywane są w polu magnetycznym wytwarzanych przez silne magnesy.
EXPERYMENTY: ze stałą tarczą i i wiązek przeciwbieżnych (E=mc2)
SLAC:W tym akceleratorze odkryto kwark C znajdujący się w cząstce psi do 9GeV -elektrony, do 3,1GeV -pozytony
FERMILAB:odkryto kwark Top 1995r.
CERN LHC- wielki zderzasz Hadronów en 7000GeV, tunel 27 km w ciągu sekundy 11000 Bozon Higgsa- jest to cząstka o masie ponad 100 mas protonów cząstki elementarne oddziaływają z polem Higgsa poprzez wymianę bozonu nabierają masy.
DESY: Odkryto gluon, KEK wykryto różnice między materią i antymaterią -Bella.
NEUTRINA wg modelu standardowego -neutrina elektronowe, mianowe, taonowe } + ich antycząsteczki. Teoretycznie istnienie neutrina przewidział Pauli 1831 natomiast w eksperymencie 1956 Reines potwierdzenie doświadczenia. NEUTRINA SŁONECZNE: z największym prawdopodobieństwem zachodzi :
p+p12d+e++Ve;7Be+e-7Li+Ve; 8B4He+4He+e++Ve, energia neutrin: pp <0,42MeV, 7Be>814keV, 8B 0-14,1 MeV NEUTRINA ATMOSFERYCZNE: powstają w reakcjach promieniowania kosmicznego z górną warstwą atmosfery. NEUTRINA ELEKTRONOWE powstałe wewnątrz słońca po 2 sekundach docierają na jego powierzchnię a po 8 docierają do ziemi. Przekrój czynny na reakcję neutrin z materią jest b.mały rzędu ~10-49m2
DETEKCJA NEUTRIN:-detektory umieszczone są w kopalniach w celu eliminacji błędów wynikających min. Tła promieniowania kosmicznego. DETEKTORY CHLOROWE: Ve+37Cl37Ar+e gdzie Ve neutrina, które mogą wywołać taką reakcję w słońcu typu 7Be, 8B, 37Ar-izotop promieniotwórczy
DETEKTORY POLOWE: Ve+37Ga71Ge+e-
Ve-neutrina pochodzące z reakcji typu pp, Ge izotop promieniotwórczy. DETEKTORY CIĘŻKOWODNE: D2o a)reakcja Ve+np+e-, gdzie e- wywołuje promieniowanie Czerenkowa, b) rozbicie deutronu Ve+dp+p+e- c)rozproszenie neutrin na lektrony. W eksperymentach otrzymywano zawsze mniej neutrin niż to wynikało z obliczeń. W detektorach z chlorem było ok. 3 razy mniej neutrin a w detektorach ciężkowodnych ok. połowę mniej (deficyt neutrin) Neutrina elektronowe po drodze ze słońca do ziemi przemieszczają się w neutrina mianowe lub taonowe - jest to zjawisko oscylacji neutrin. Wszystkie eksperymenty prowadzone przy wykorzystaniu omówionych detektorów potwierdzaja iż neutrina mają niewielką masę (niezerową)
WSZECHŚWIAT BUDOWA-płyn doskonały , gęstość materii jest stała (jednorodnie rozłożona w przestrzeni energia i materia) 1Mpc=3*1022m, 1pc=3 lata świetlne. Nasza galaktyka 30 tyś PC
1929-Edvin Hubble -wszechświat się rozszerza, 1927-Lemaitve- pierwszy twórca teorii wielkiego wybuchu, 1948 Gamrow też wielki wybuch, 1965- Pehzias, Wilson -okrycie reliktowego promieniowania tła (efekt doplera)
SATELITY 1992 COBE,WMAP -satelity rejestrujące promieniowanie reliktowe wykryły niejednorodności w rozkładzie materii we wszechświecie który miał 300 tyś lat
EWOLUCJA WSZECHŚWIATA: a)0-10-43s -Era Planca, gęstość materii -energii 1097 kg/m3, temp. 1032K, Obecne prawa fizyki nie dają informacji o wydarzeniach w Erze Planca. b) 10-43-10-35s Era wielkiej unifikacji -wszystkie oddziaływania z wyjątkiem grawitacyjnego są równoprawne w temp 1028 K -oddziaływanie silnie oddzieliło się od oddziaływania słabego i elektromagnetycznego. c) 10-35s -10-33 Era inflacji wszechświat przyspiesza swoje rozszerzanie się.
d) 10-33 -10-5 Era plazmy glonowo -kwarkowej T= 3*1012K. kwarki łączą się w protony i neutrony powstała nadwyżka materii nad antymaterią e) 1s-4 min Era nukleosyntezy T=109K -powstają lekkie jądra 2H, 3H, 3He, 4He, 7Li promieniowanie elektromagnetyczne nie może pokonać dużej drogi bo wciąż oddziałuje z jądrami - wszechświat nie jest przezroczysty. f) 4 min -3000000lat Era rozprzęgania materii i promieniowania T=104K - powstają atomy, a promieniowanie elektromagnetyczne może przebywać drogę bardzo dużą - wszechświat staje się przezroczysty. Wtedy wysłane fotony zarejestrowane jako promieniowanie reliktowe miały energię odpowiadającą 2,73K, g) 300000-2mld lat -powstają galaktyki, h) 2 mld chwila obecna -tworzenie się układów planetarnych
PRAWO HUBBLE'A V=H*d -prędkość oddalania się galaktyk jest proporcjonalna do odległości między nimi. V-prędkość, H- stała Hubble'a, d-odległość między galaktykami. Wg danych z sondy WMAP wiek wszechświata 13,7 mld lat, WMAP -sonda umieszczona od ziemi 1,5 mln km w tgz. Punkcie libacyjnym (tyłem do słońca ziemi i księżyca) wynik z sondy: wiek wszechświata 13,7 mld lat , model płaski wszechświata, ilość materii barionowej 4-5%, ilość ciemnej materii 23-25%, ilość ciemnej energii 70-73%. CIEMNA MATERIA: a) gorąca to prawdopodobnie neutrina w liczbie 1087 b) to tzw cząstki super symetryczne 1072 np. neutrino, bozon, superpartrela fotonu)
DETEKTORY DO REJESTRACJI CIEMNEJ MATERII: a) kriogeniczne :rejestracja impulsu cieplnego wywołanego przez cząstkę ciemnej materii (german, tlenek glinu) b) scyntylacyjne- rejestracja impulsu świetlnego -ciekły ksenon)
PRZYSZŁE LOSY WSZECHŚWIATA: Ω-gęstość krytyczna, Ω<1 -model otwarty, Ω=1 model płaski, Ω>1 model zamknięty (czas oś x)
CIAŁO STAŁE: Budowa krystaliczna: 1 Śieć krystaliczna -układ punktów przestrzeni regularnej (sieć+baza=struktura) , parametry ścian α ā; β ъ ; ĉ γ
TABELA 1!!!
Współ czynnik upakowania k
K=(objętość wszystkich atomów w komórce elementarnej )/(objętość komórki elementarnej)
Dla sieci F
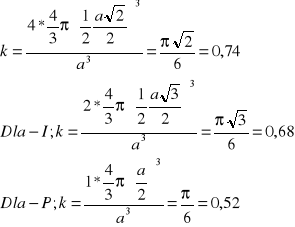
Dla sieci heksagonalnej współczynnik upakowania także wynosi k=0,74
WSKAŹNIKI MILLERA
1.Dla węzłów sieci krystalicznej - jest to 3 cyfry: m,n,p
2.Dla kierunków [h,k,l]
3.Dla płaszczyzn [h,k,l]
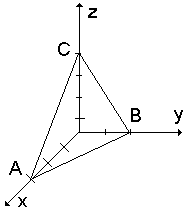
1) A=3, B=2, C=4 2) odwrotność 1/3, ½, ¼ 3)najmniejszy wspólny mianownik D=12 4) wskaźnik Millera h=D/A=4, k=D/B=6, l=D/C=3 (4,6,3)
Gdy płaszczyzna jest równoległa do danej płaszczyzny o współczynnikach (h,k,l) posiada takie same wskaźniki. Jeśli płaszczyzna przecina os w nieskończoności jej wskaźnik wynosi 0. Przykład dla układu regularnego:
WIĄZANIA KRYSTALICZNE: W kryształach siły przyciągania między atomami nie ulegają nasyceniu (tzn. że po dodaniu kolejnego nowego atomu kryształ rozrasta się) Energia spójności - różnica pomiędzy energią zbioru swobodnych atomów a energią kryształu lub energia potrzebna do rozłożenia kryształu na składowe atomy jest ona: - największa dla kryształów jonowych (~10eV/atom) dla metali przejściowych (~7eV/atom) - średnia dla metali alkaicznych (sód, potas, grupa I ) ~1eV/atom, -najmniejsza dla kryształów molekularnych (kryształy gazów szlachetnych ~0,1vE/atom) tabelka 2!!!
METODY BADANIA STRUKTUR KRYSZTAŁÓW (SIECI)
I METODY DYFRAKCYJNE:
1.Promieniowanie rentgenowskie: powstawanie widma i własności. 2. Rozproszenie promieniowania na atomach: warunki Lauego. 3. Prawo Bragga; 4.metody doświadczalne a) metoda Lauego; b) metoda obracalnego kryształu, c) metoda proszkowa;
Ad1. Lampa rentgenowska: bombardowanie elektronami tarczy np. miedzianej:
Widmo promieniowania:
eU=h(c/λ) , graniczna długość fali λgr=(hc)/(eU)
Widmo hamowania: Gdy elektrony mają bardzo dużą energię mogą wybić elektrony z powłoki K,L,M…. atomu tarczy-powstaje tzw promieniowanie charakterystyczne.
λ=10-8-10-10m już dla 35 tyś Volt.
WŁASNOŚCI PROMIENIOWANIA X:
-zaczernianie kliszy fotograficznej, - świecenie platynocyjanku boru; -wywołanie zjawiska fotoelektrycznego i Camptona; -dyfrakcja na kryształach.
Promieniowanie X twarde- dotyczy linii k (serie widmowe Kα, Kβ )
Promieniowanie X miękkie- serie Lα, Lβ i Mα, Mβ… kolejne powłoki)
Naturę falową promieni X potwierdził w 1914 roku Von Laue, przeprowadzając dyfrakcję na kryształach Nall. W każdym przypadku dyfrakcji musi być spełniony warunek: rozmiar odległości oczek na siatce dyfrakcyjnej musi być zbliżony bądź równy długości fali promieniowania!
Ad2.
d-odległość między atomami, stożek ugięcia
-różnica dróg optycznych Δl
Δl=a-b; a/d=cosφ; b/d=cosΨ
-warunek wzmocnienia: Δl=h*λ , h-liczba całkowita
![]()
-d(cosφ- cosΨ)=h*λ -warunek Lauego
Przypadek 3 wymiarowy: równania Lauego
d1(cosφ1- cosΨ1)=h*λ
d2(cosφ2- cosΨ2)=h*λ
d3(cosφ3- cosΨ3)=h*λ
Aby zaszła interferencja konstruktywna wszystkie poniższe 3 równania Lauego muszą być jednocześnie spełnione (wszystkie 3 stożki ugięcia mają wtedy wspólną tworzącą)
Ad3.
Δl=CB+BD, CB/d=sinΘ, Δl=2dsinΘ, BD/d= sinΘ, Θ-kąt Brogga (kąt połysku)
Warunek wzmocnienia: 2dsinΘ= n*λ- prawo Brogga gdzie n- rząd ugięcia
Warunki Lauego i prawo Brogga są równoważne, przy warunkach Lauego bierzemy pod uwagę osie kryształu, w przypadku prawa Brogga wybieramy określone płaszczyzny, a osią jest odległość między płaszczyznami d.
Ad4.W metodach dyfrakcyjnych należy pamiętać o tym aby długość była tego samego rzędu wielkości co badanego obiektu. Badania polegają na zmianie któregoś z parametrów w równaniach Lauego lub Brogga: λ; Θ;
Metoda Lauego do badania monokryształów wykorzystuje się tzw białe promieniowanie (promienie X o długościach fal z pewnego zakresu- próbka zamieszczona jest na stałe)
Próbki mają wymiar dł. 1mm. Kryształ, wybiera się z wiązki promieni te długości fali dla , których spełnione są warunki Lauego. Metoda ta pozwala n a określenie symetrii kryształu i niedoskonałości struktury wywołane obróbką termiczną lub mechaniczną.
Metoda obracanego kryształu:
Kryształ w skutek obrotów może być tak ustawiony, że można zmierzyć refleksy dyfrakcyjne od dowolnych płaszczyzn (h,k,l)
-promieniowanie monochromatyczne; -próbka monokryształu obraca się.
Metoda prążkowa (Debye'a - Scherrera)
-monochromatyczne promieniowanie; -próbka polikryształu - zapewnia prawie ciągłą zmianę kąta Θ.
Krystality w polikrysztale ustawione są przypadkowo. Zawsze któryś jest zorientowany tak, że spełnia warunek dyfrakcji dla którejś rodziny płaszczyzn sieciowych.
Uzyskuje się widmo: z dyfraktogramu można uzyskać info o: -typie sieci krystalicznej; - stałych sieciowych; -odkształceniu sieciowym; -średnich rozmiarach ziaren;
D- średnica D=(hλ)/(B(2Θ)cosΘ) , k-stała Scherrera = 0,89
MODEL ELEKTRONÓW SWOBODNYCH:
Założenia: -elektrony walencyjne atomów (w metalach jest ich 1-3) są swobodne i tworzą gaz doskonały; -elektrony poruszają się w trójwymiarowej studni potencjału (elektrony nie opuszczają metalu); -elektrony nie oddziałują z siecią jonów.
Równanie Schrodingera: Hφ =EΨ -funkcja własna, gdzie Hφ-operator energii, EΨ- energia własna.
![]()
Rozwiązanie, funkcja falowa , która ma postać:
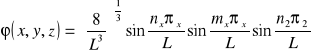
Energia własna:
![]()
n- liczba kwantowa
Jeżeli n oznacza liczbę elektronów to możliwych zatem liczb dodatnich równać się będzie ½ n -to wynika z zależności Pauliego.
Niech :![]()
- będzie promieniem kuli w przestrzeni liczba stanów równa będzie objętości jednej ósmej kuli.
![]()
nmax2=(3N/Π)2/3 Energia max jaką mogą posiadać elektrony w krysztale to energia Fermiego:
Ef=(ħ2Π2/2ml2)*(3N/Π)2/3
Objętość V=L3; Ef=(ħ2Π2/2ml2)*(3/Π*N/V)2/3 gdzie N/V -u- koncentracja
Ciśnienie gazu Fermiego: p=2/3n <E> gdzie n - liczba moli gazu, <E> - srednia energia; <E>=3/5 Ef; p=2/3h3/5Ef=2/5hEf dla Cu p=3,8*10^5 atmosfer. Nawet w temperaturze 0 stopni K elektrony mają dużą energię i poruszają się z dużymi prędkościami. Energie te są wiele razy większe od energii ruchów termicznych. Aby energia Fermiego Ef= Et to temperatura gazu musi być rzędu 50000K. Funkcja gęstości stanów 6n - przestrzeń wymiarowa. Element objętości: dΓ=dFv*dΓp; dxdpc=h, w objętości: dΓ=h3 jest 2 elektrony na 1 elektron przypada objętość h3/2
dΓ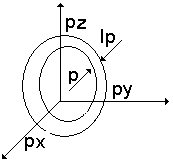
p=4Π2dp; liczba elektronów dla ъdΓ=1
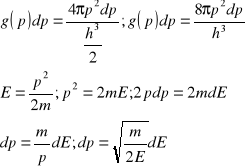
Funkcja gęstości stanów (w przestrzeni energii):
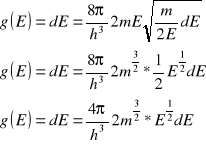
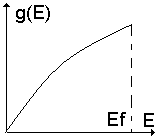
Koncentracja elektronów: 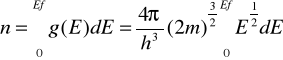
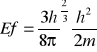
Energia średnia:
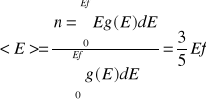
Średnia prędkość:
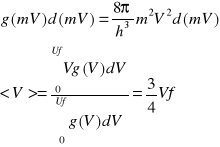
Wpływ temperatury na energię Fermiego: dla 0°K. dla: E<Ef f(E)=1, dla temp >0°K E>Ef f(E)=0, dla E<Ef f(E)<1, E>Ef f(E) >0
Funkcja Fermiego - Diraca:
![]()
Koncentracja elektronów = liczba stanów energetycznych
MODEL PASMOWY KRYSZTAŁU:
-uwzględniamy oddziaływanie elektronów z siecią krystaliczną; -potencjał sieci opisujemy funkcją okresową (bo sieć jest periodyczna) ; -funkcja falowa elektronu uwzględnia periodyczność sieci (ma ona postać funkcji Blocha) Ψ(x)=u(x)eihx
POTENCJAŁ SIECI WG KRONIGA-PENNECJA:
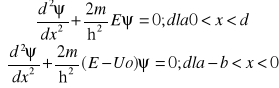
Pasmo energetyczne w zależności od odległości między atomami MODEL PASMOWY:
PRZEWODNICTWO ELEKTRYCZNE:
1.OBRAZ KLASYCZNY
-Natężenie prądu elektrycznego
![]()
Jednostka: 1 amper, 1A.
Gęstość prądu elektrycznego
![]()
W nieobecności zewnętrznego pola elektrycznego elektrony poruszają się chaotycznie we wszystkich kierunkach. W zewnętrznym polu E uzyskują wypadkową (stałą z założenia) prędkość unoszenia vu.
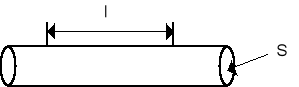
Jeżeli n jest koncentracją elektronów to ilość ładunku Q jaka przepływa przez przewodnik o długości l w czasie t = l/vu wynosi![]()
Q = nSle
Tak więc natężenie prądu wynosi
![]()
![]()
a gęstość prądu
gdzie q jest gęstością ładunku.
Przykład:
Prąd o natężeniu 1A płynie w drucie miedzianym o przekroju 1 mm2. Jaka jest średnia prędkość unoszenia elektronów przewodnictwa ? Masa atomowa miedzi μ = 63.8 g/mol, a gęstość ρ = 8.9 g/cm3.
Z równania na natężenie prądu otrzymujemy
![]()
Zakładamy, że na jeden atom przypada 1 elektron przewodnictwa (Cu+1). Możemy więc obliczyć koncentrację nośników
![]()
n = 8.4·1028 atom/m3
Wstawiając do równania na prędkość otrzymujemy
vu = 7.4·10-5 m/s = 0.074 mm/s
Prądy mogą też płynąć w gazach i cieczach. Lampy jarzeniowe są przykładem wykorzystania przepływu prądu w gazach. W gazach prąd jest wynikiem ruchu nie tylko elektronów ale i jonów dodatnich. Jednak lżejsze elektrony są znacznie szybsze i ich wkład do prądu jest dominujący. W zderzeniu elektronu z jonem lub atomem gazu energia może zostać zaabsorbowana przez atom, a następnie wypromieniowana w postaci promieniowania elektromagnetycznego w tym również widzialnego.
2.OBRAZ KWANTOWY
Model elektronów swobodnych dobrze opisuje przewodnictwo metali jednowartościowych. Stosujemy go przy założeniu, że elektrony rozpraszają się na jonach sieci:
Przestrzeń k:
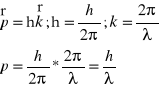
Gaz elektronów znajduje się w stanie równowagi, energia elektronów nie przekracza energii Fermiego. W przestrzeni pędu (h) możemy wyróżnić elektrony o pędzie
![]()
, całkowity pęd układu wynosi 0. Po przyłożeniu pola elektrycznego z zewnątrz na każdy elektron działa siła, która powoduje unoszenie elektronów, elektrony zderzają się z jonami sieci i jednocześnie poruszają się uporządkowanym ruchem z prędkością unoszenia (dryfu). Kula Fermiego przesuwa się ponieważ elektrony uzyskują dodatkowy pęd przesunięcia ![]()
prędkość dryfu
Po przyłączeniu zewnętrznego pola E elektrycznego kula się przesuwa. Tylko elektrony z pobliża powierzchni Fermiego biorą udział w transporcie. Ruch elektronów opisuje druga zasada dynamiki:
![]()
m*-masa efektywna ,τ-czas relaksacji, czas kiedy po odłączeniu zewnętrznego pola E kula powraca do stanu początkowego.
Gęstość prądu: j=-heVd; Vd=ατ, j=((ne2τ)m*)E
Ruchliwość: μ=eτ/m*, ogólne δ=e(nμc+pμp)
Elektrony w sieci krystalicznej zachowują się jakby miały masę inną niż masa elektronu swobodnego, jest to tzw. masa efektywna, która może być mniejsza lub większa od masy elektronu swobodnego, ujemna lub anizotropowa.
ZALEŻNOŚĆ PRZEWODNICTWA OD TEMPERATURY:
δ=(ne2τ)/m*, τ=Λ/V gdzie: Λ-średnia droga swobodna, V-prędkość na powierzchni Fermiego.
Koncentracja praktycznie nie zależy od temperatury, podobnie Vf, tak więc wielkością zależną od temperatury jest średnia droga swobodna Λ. Elektrony rozpraszają się na 1) fononach, 2) domieszkach. Fonony są to kwanty drgań sieci krystalicznej.
„RYS. SZEŚCIAN KULKI NA ROGACH FALBANKA „
Ad1. Λ-zależy od liczby centrów rozpraszających Λ~1/N; dla niskich temperatur Nfononów~T3,
dla wysokich temperatur Nfononów~T
Λ~1/T3 , Λ~1/T =>δΛ~, g~1/Λ to wszystko
ρ~T dla wysokich temperatur oraz ρ~T5 dla niskich temperatur
REGUŁA HOTHIESSENA:
ρ=ρ1+ρ2+ρ3+ρ4+….
W szerokim zakresie temperaturowa zależność ρ=F(T) jest liniowa i przedstawiają wzór empiryczny: ρ=ρo[1+α(T-To)]
α- temperaturowy współczynnik oporu
PRZEWODNICTWO CIEPLNE A PRZEWOPDNICTWO ELEKTRYCZNE
W klasycznej teorii metali (teoria Drudego) zakłada się że ciepło w przewodnikach przenoszone jest przez eketrony przewodnictwa. Założenie to opiera się na fakcie doświadczalnym dotyczącym znacznie lepszego przewodnictwa cieplnego metali w porównaniu z dielektrykami. Teoria Drudego dobrze wyjaśnia prawo Wiedemanna- Franza które mówi, że stosunek przewodnictwa cieplnego do elektrycznego jest wielkością stałą i w ~ taka samą dla wszystkich metali χ/δ=const
Przewodnictwo cieplne opisuje prawo Fouriera
Q= - χdT/dx, dT/dx-gradient temperatury , w oparciu o teorie kinetyczną gazów można stwierdzić że χ=1/3CvVl gdzie Cv -ciepło właściwe przy stałej objętości, V- średnia prędkość cząstki, l- średnia droga swobodna,
Cv=3/2 n*k*B gdzie B- stała Boltzmana.
W obliczeniach Drudego δ=me2τ/2m i dwójka w mianowniku dawała wyniki dobrze zgadzające się z doświadczeniem.
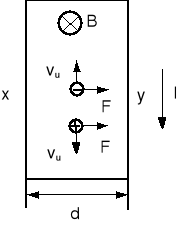
ZJAWISKO HALLA:
Jeżeli płytkę metalu (lub półprzewodnika) umieścimy w polu magnetycznym, prostopadłym do kierunku przepływu prądu, to na ładunki będzie działała siła odchylająca powodująca zakrzywienie torów ładunków w kierunku jednej ze ścianek bocznych płytki. Niezależnie czy prąd jest związany z ruchem ładunków dodatnich czy ujemnych mamy do czynienia z odchylaniem ładunków w kierunku jednej krawędzi. Przesunięcie ładunków powoduje powstanie poprzecznego pola elektrycznego Halla EH. To pole przeciwdziała dalszemu przesuwaniu ładunków. Pole Halla jest dane wzorem:
![]()
W stanie równowagi odchylające pole magnetyczne jest równoważone przez pole elektryczne: qEH + q(vu × B) = 0
Stąd: EH = - vu × B
Wynika stąd, że jeżeli zmierzymy EH i B to możemy znaleźć vu.
Gdy vu i B są prostopadłe to: EH = vuB
Ponieważ: vu = j/Ne, więc EH = (jB)/(ne) lub n = (jB)/(eEH)
Możemy wyznaczyć n. Można też wykorzystać ten efekt do pomiaru pola magnetycznego.
PÓŁPRZEWODNIKI
1.Pierwiastki Si, Ge, C, B, P, S, Se, Sn, Sb, Te, I
2. Związki typu AIII BV GaAs, Gap, IaSb, związki AIIBVI np. CdS, ZnO
Półprzewodniki dzielimy na samoistne i domieszkowe. Stosując efekt Halla można doświadczalnie wyznaczyć koncentrację nośników i z wykresu Arheniusa otrzymać wielkość przerwy energetycznej Eg.
Koncentracja nośników w p/p samoistnym:
![]()
Koncentracja nośników wzrasta wraz ze wzrostem temperatury.
POZIOM FERMIEGO
W temp 0 K Ef=Eg/2 ; T> 0K Ef=Eg/2+3/4kbT ln(mp*/mn*)
PÓŁPRZEWODNIKI DOMIESZKOWANE
Domieszkowanie umożliwia nam szeroką zmianę oporu właściwego półprzewodnika, a jest to około 10 rzędów wielkości. Do domieszkowania używa się głównie pierwiastków III i V grupy. Domieszki z pierwiastkami III grupy pozwalają na otrzymanie akceptorów (wytwarza się dziura), a z grupy V dostarczają donorów.
PRZEWODNICTWO ELEKTRYCZNE PÓŁPRZEWODNIKÓW
δ=[e](nμn+pμp), μ=eτ/m*, δ-zależy od wzrostu n i spadku μ (zależy od temperatury)
Odcinek AB: tgα1=Ej/2kB - temperatura wzrasta przewodnictwo też wzrasta. Ej energia jonizacji.
ZŁĄCZE PN nazywane jest złącze dwóch półprzewodników niesamoistnych o różnych typach przewodnictwa: P i N. W obszarze typu N występują nośniki większościowe ujemne (elektrony) oraz unieruchomione w siatce krystalicznej atomy domieszek (donory). Analogicznie w obszarze typu P nośnikami większościowymi są dziury o ładunku elektrycznym dodatnim oraz atomy domieszek (akceptory). W półprzewodnikach obu typów występują także nośniki mniejszościowe przeciwnego znaku niż większościowe; koncentracja nośników mniejszościowych jest dużo mniejsza niż większościowych.
Dioda LED (ang. Light Emitting Diode) - dioda zaliczana do półprzewodnikowych przyrządów optoelektronicznych, emitujących promieniowanie w zakresie światła widzialnego, jak i podczerwieni.
Jej działanie opiera się na zjawisku rekombinacji nośników ładunku (rekombinacja promienista). Zjawisko to zachodzi w półprzewodnikach wówczas, gdy elektrony przechodząc z wyższego poziomu energetycznego na niższy zachowują swój pseudo-pęd. Jest to tzw. przejście proste. Podczas tego przejścia energia elektronu zostaje zamieniona na kwant promieniowania elektromagnetycznego. Długość fali generowanego promieniowania:
przy czym: Wg = Wc - Wv - szerokość pasma zabronionego lub różnica energii poziomów, między którymi zachodzi rekombinacja, c - prędkość światła, h - stała Plancka.
NADPRZEWODNICTWO:
1911 Heiko Kamerling Ommes -doświadczenia nad rtęcią. Wynikiem badań było:

Tk=4,2K-teperatura krytyczna dla rtęci
Nadprzewodnictwo charakteryzuje się:
1.zerowym oporem elektrycznym, 2.doskonałym diamagnetyzmem.
Namagnesowanie: ![]()
Podatność magnetyczna χ=M/H gdzie H- natężenie makroskopowe pola magnetycznego, gdy χ<0 wówczas diamagnetyki a gdy χ>0 -paramagnetyki. Zachowanie się nadprzewodnika w polu magnetycznym, Onnes zauważył że gdy natężenie prądu przekroczyło pewną wartość krytyczną, stan nadprzewodnika zniknął.
![]()
Efekt Meissnera- p.mag. jest wypychane przez diamagnetyki w nadprzewodniku.
Ha+4ΠM=0, 4ΠM=-Ha, χ=M/Ha , χ=-1/4Π <0 czyli nadprzewodnik jest idealnym diamagnetykiem.
NADPRZEWODNIKI I I II RODZAJU:
W 1957r. Abrikosow, analizując zachowanie nadprzewodników w zewnętrznym polu magnetycznym, odkrył, iż należy rozróżnić dwa rodzaje nadprzewodników: nadprzewodniki I i II rodzaju.
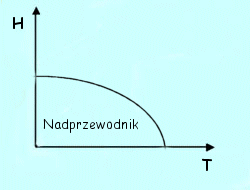
Nadprzewodniki I rodzaju wypychają całkowicie strumień magnetyczny ze swojego wnętrza, natomiast nadprzewodniki II rodzaju zachowują się tak tylko w słabym polu magnetycznym; w silnych polach strumień magnetyczny jest wypychany z ich wnętrzach tylko częściowo. Dzięki takiemu zachowaniu, tzn. utworzeniu stanu mieszanego, nadprzewodniki II rodzaju pozostają nadprzewodnikami nawet w polach magnetycznych o indukcji większej niż 10T.
Nadprzewodniki I rodzaju
Wykres fazowy dla nadprzewodnika I rodzaj
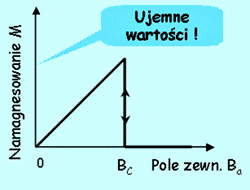
Zmiany namagnesowania w funkcji zewnętrznego pola magnetycznego dla nadprzewodników I rodzaju.
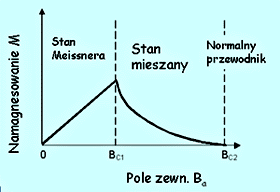
Nadprzewodniki II rodzaju. W przypadku nadprzewodników II rodzaju mamy do czynienia z dwoma polami krytycznymi: dolnym HC1 i górnym HC2. Strumień jest wypychany całkowicie jedynie poniżej dolnego pola HC1 i wówczas nadprzewodnik zachowuje się identycznie jak nadprzewodnik I rodzaju poniżej HC. Powyżej HC1 strumień zaczyna częściowo wnikać do próbki aż do osiągnięcia górnego pola krytycznego HC2. Powyżej HC2 próbka przechodzi w stan normalny.
Zmiany namagnesowania w funkcji zewnętrznego pola magnetycznego dla nadprzewodników II rodzaju.
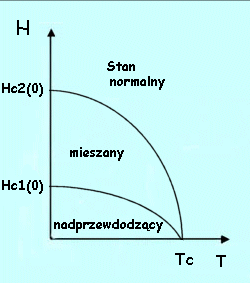
Zależność pól krytycznych HC1 i HC2 od temperatury dla nadprzewodników II rodzaju.Górne pole krytyczne może przybierać bardzo duże wartości, nawet powyżej 100 T. Pomiędzy dolnym i górnym polem krytycznym próbka znajduje się w stanie mieszanym. Wypychanie pola jest tylko częściowe. Dla wszystkich zewnętrznych pól magnetycznych o natężeniu HC1 << H << HC2, strumień magnetyczny częściowo wnika do próbki w postaci włókien o mikroskopowych rozmiarach tzw. vortex'ów. Jeśli H << HC1 strumień jest wypychany całkowicie. Tak więc we wnętrzu nadprzewodnika B = 0, powyżej HC2 próbka jest w stanie normalnym. Za pomocą mikroskopu elektronowego można obserwować sieć wirów okazuje się ze sieć ta ma postać trójkątną. Sieć tę można też obserwować za pomocą technik tzw. dekoracyjnych. Powierzchnię nadprzewodnika posypuje się drobnymi cząstkami ferromagnetyka a następnie przykłada się pole magnetyczne. Magnetyczne cząstki układają się w obszarach odpowiadającym rdzeniom wirów i pozostają tam także po ogrzaniu do temperatury pokojowej.
WŁAŚCIWOŚCI MAGNETYCZNE MATERIAŁÓW:
1. Moment magnetyczny: ![]()
, w atomie:![]()
2.Podatność magnetyczna:
χ=M/H m-namagnesowanie, H- pole magnetyczne makroskopowe.
3.Przenikalność magnetyczna: dla próżni
,
Jeśli ośrodkiem jest paramagnetyk lub diamagnetyk przenikalność magnetyczna jest również skalarem, i można zapisać że:
![]()
gdzie: μr - względna przenikalność magnetyczna ośrodka (liczba bezwymiarowa) określana jakos stosunek przenikalności magnetycznej danego ośrodka do przenikalności magnetycznej próżni.
Dla paramagnetyków przenikalność względna jest niewiele większa od 1, dla diamagnetyków jest niewiele mniejsza od jedności, dla próżni tożsamościowo przenikalność względna jest równa dokładnie 1.
![]()
W przypadku ferromagnetyków przenikalność względna nie może zostać opisana jedną liczba (skalarem). Dla jednoosiowego przemagnesowania przenikalność względna ferromagnetyków określana jest nieliniową funkcją.
![]()
W celu zaprojektowania danego obwodów magnetycznych stosuje się uproszczenie przenikalności do jednej wartości w danym punkcie pracy urządzenia. W takim przypadku konkretną wartość przenikalności oblicza się jako:
gdzie: Bm - szczytowa wartość przebiegu indukcji magnetycznej, Hm - szczytowa wartość przebiegu natężenia pola magnetycznego.
Funkcja ta ma pewną początkową niezerową wartość zwaną przenikalnością początkową, następnie osiąga maksimum (przenikalność maksymalna) po czym dla bardzo wysokich wartości pola magnetycznego, przy którym następuje nasycenie materiału wartość ta zbliża się do jedności (przenikalność względna materiału zbliża się do wartości przenikalności próżni).
![]()
![]()
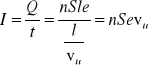
![]()
Wyszukiwarka