Wykład 1

EKONOMIA MATEMATYCZNA jest to dyscyplina naukowa, która obejmuje różnorodne zastosowania matematycznych pojęć, metod i teorii w ekonomii, a zwłaszcza- w teorii ekonomii.

Teorie: przedsiębiorstwa, oligopolu, równowagi konkurencyjnej, wzrostu gospodarczego.

Korzyści:

-bardziej precyzyjne formułowanie teorii

-otrzymanie z teoretycznego punktu widzenia wyników czasami niemożliwych do otrzymania w matematyce

-

EKONOMIA MATEMATYCZNA jest matematyką stosowaną, „spółka” matematyki z ekonomią.

EKONOMIE MATEMATYCZNĄ najlepiej jest uważać za proces wyprowadzenia wniosków z jakiegoś szczególnego zbioru niesprzecznych aksjomatów mających....

Etapy działania ekonomii matematycznej:

1. Przyjmuje się wstępne założenia o badanym obiekcie ekonomicznym i formułuje się je w języku matematyki

2. Posługując się pojęciami odpowiednich teorii matematycznych i korzystając z twierdzeń i metod tych teorii z przyjętych założeń wyprowadza się wnioski, stawia hipotezy i otrzymuje się rozwiązania postawionych problemów.

W ekonomii matematycznej charakterystyczne jest to, że rozpatrywane są typowe obiekty (konsument)

Rys historyczny. Prekursorzy i mistrzowie myśli ekonomicznej.

Ekonomia matematyczna wyłoniła się z historii ekonomii w latach 30 XIX w.

Francois Quesnay- ekonomista francuski (1694- 1774) podjął próbę stworzenia systemu wyjaśniającego mechanizmy rządzące gospodarką narodową. W 1759 r wydał dzieło pt. „Tableau economique” które jest uważane za pierwowzór tzw. Modelu przepływów międzygałęziowych Leontiefa. Mistrz szkoły ekonomicznej zwanej fizjokratyzmem.

Za prekursora ekonomii matematycznej, prekursora szkoły lozańskiej uważany jest Antoine Augustin Cournot (1801-1877). Napisał w 1838 „Badania nad zasadami teoretycznymi teorii bogactwa”. Posługiwał się rachunkiem różniczkowym, który jako pierwszy wprowadził do ekonomii.

Cesare Bonesana di Beccaria- zwolennik fizjokratyzmu . „Elementy ekonomii politycznej”

Leon Wal ras (1834-1910) mistrz szkoły lozańskiej. „Elementy czystej ekonomii politycznej”. Podstawy teorii równowagi ogólnej, stosował analizę matematyczną.

W.S. Javons (1824-1910)

Vilfredo Pareto (1848-1923)

Szkoła lozańska stworzyła teorię... firmy , oligopolu.

Obok szkoły austriackiej (psychologicznej) i angloamerykańskiej (neoklasycznej) była jedną z głównych szkól tworzących kierunek marginalistyczny.

Przedstawiciele szkoły austriackiej: Karl Mengel-mistrz

Przedstawiciele angloamerykańskiej: Jevons-mistrz

Pierwszy okres w historii ekonomii kończy się w latach 30-40 XX w dziełami :

J.R. Hicks „Wartość i kapitał” 1931

P.A. Samuelson „Podstawy analizy ekonomicznej” 1947

Michał Kalecki „Teoria cyklu biznesowego” 1937

„A Theory of business cycle”

Drugi okres w ekonomii matematycznej to lata 1948-1959 -okres modeli mnogościowych i liniowych.

Grupy zagadnień:

Pierwsza grupa osiągnięć- prace z równowagi teorii ekonomicznej:

G. Debren „Teoria wartości: aksjomatyczna analiza równowagi ekonomicznej” 1955

K. J. Arrow

Druga grupa

Pracec z zakresu ekonomicznych zastosowań programowania matematycznego

T. Ch. Koopmans

L. Kantorowicz

Prace z teorii przepływów międzygałęziowych

Matematyczne modele wzrostu gospodarczego i dynamiki gospodarczej

R. M. Solow

R. F. Harrod

E. D. Domer

Zagadnienia teorii gier

J. von Leumann

O.Morgenstern

J.F. Nash

Nobliści :

1994 John Charles Harsony, John F. Nash, Reinhard Selten- równowaga w teorii gier

1987 Robert M. Solow -teoria wzrostu gospodarczego

1983 Gerard Debreu- nowe metody analityczne w ekonomii

1973 Wassily Leontief- przepływy międzygałęziowe

1972 Sir John R. Hicks oraz Kenneth J. Arrow- ogólna teoria równowagi oraz teorii dobrobytu

1970 Paul Anthony Samuelson- statystyczna i dynamiczna teoria ekonomii

Wykład 2

Elementy popytu indywidualnego konsumenta

Zał.

Towary są nieskończenie podzielne i jednorodne

Przestrzeń towarów

Zał.

Na rozpatrywanym rynku znajduje się n różnych towarów

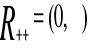
n-ta potęga kartezjańska

Def

Wektor x=(x₁, x₂...x_i,...x _n)∈R₊ⁿ, w którym i-ta współrzędna reprezentuje ilość i-tego towaru, którą konsument ewentualnie może kupić, wyrażoną w jednostkach naturalnych nazywamy koszykiem towarów (wiązka towarów)

X-zbiór wszystkich dostępnych na rynku koszyków towarów

Przykład1

N=4

X=(1, 2, 0, 2)

Y=(0, 3, 1, 5)

Wprowadzamy w zbiorze * metrykę z

X=(x₁, x₂,... x _n)

Y=(y₁, y₂,... y _n)

X=(1,2,0,2)

Y=(0,3,1,5)

Definicja

Przestrzenią towarów będziemy nazywali parę (X,d) gdzie X-zbiór wszystkich dostępnych na rynku towarów, a d jest metryką zdefiniowaną (*)

Przykład2

X0=(1,1)

R=1

K(x0,r)

1

1

Relacje preferencji konsumenta

To, który z koszyków konsumetn wybierze zależy od jego preferencji

Preferencje konsumentów można formalnie scharakteryzować za pomocą relacji w przestrzeni towarów X x,y∈X

Konsument silnie preferuje koszyk x nad koszyk y

Konsument woli koszyk y niż x

x∼y

konsument uważa koszyki za jednakowo dobre , koszyki x i y są indyferentne

Def

Relacją obojętności w postaci x nazywamy zbiór

I={(x,y)∈X*X|x∼y} I⊂X2

Zał

Relacja obojętności jest zwrotna , symetryczna przechodnia-jest relacją równoważności

Def

Relacją silnej preferencji konsumenta nazywamy zbiór:

Ps⊂x2

Zał

Relacja silnej preferencji jest przechodnia

Def

Relacją słabej preferencji nazywamy zbiór:

- konsument słabo preferuje x nad y lub konsument uważa koszyk x za niegorszy od y

Zał

Relacja słabej preferencji jest przechodnia i zupełna. Zupełność relacji

Preporządek- zwrotna i przechodnia

Pełny porządek-zwrotna, przechodnia i zupełna

Wyżej zdefiniowana relacja słabej preferencji jest przykładem pełnego preporządku w przestrzeni towarów i usług.

P=Ps∪I-w sensie mnogościowym

Związki między relacjami:

Twierdzenie1

Dla wolnych koszyków x, y, z∈X:

1. x>y ∨ y>x ∨ x∼y

2.

3.

4.

Definicja

Pole preferencji konsumenta to para

Dla każdego koszyka x∈X można zdefiniować;

Zbiór koszyków nie gorszych niż x:

Zbiór koszyków nie lepszych niż naszych X

Zbiór koszyków indyferentnych-względem koszyka x

Krzywą obojętności po raz pierwszy zastosował w ekonomii F.J. Edgeworth (druga poł XIXw)

Zbiór koszyków lepszych niż koszyk x

Zbiór koszyków gorszych niż koszyk x

Przykład 3

Dobra doskonale komplementarne to dobra, które mogą być konsumowane jedynie razem i w stałych proporcjach.

Cola

Własności:

1. Monotoniczność

Def

Relację

nazywamy monotoniczną, jeżeli dla każdych koszyków

x=(x₁,...x _n)∈X oraz y=(y₁,...y _n)∈X zachodzi implikacja

x>y⇒x>y

W której zapis x>y oznacza, że xi>yi dla i=1,2,...n. Jeśli relacja słabej preferencji jest monotoniczna to konsument kieruje się zasadą „im więcej tym lepiej”

2. Ciągłość relacji słabej preferencji

Def

Relację ≥ nazywamy ciągła w przestrzeni X jeżeli dla każdych dwóch koszyków x,y∈X takich, że x>y istnieje otoczenie Ux⊂X oraz Uy ⊂X takich, że:

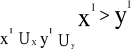
Interpretacja ciągłości:

1. Gdy relacja preferencji konsumenta jest ciągła i konsument uważa koszyk x za lepszy niż y to uważa on również każdy koszyk x ^I „niewiele” różniący się od koszyka x za lepszy od każdego koszyka y ^I „niewiele” różniącego się od koszyka y.

2. x∈X⊂R₊ⁿ

Jeżeli relacja ≥ jest ciągła to odcinek w Rⁿ łączący dowolny punkt y∈S ^>_x z dowolnym punktem z∈S ^< _x musi mieć niepustą część wspólną ze zbiorem obojętności K _x.

Przykład 4

Załóżmy że na rynku handluje się jednym doskonale podzielnym towarem którego podaż a (a>0)

Konsument ocenia koszyki następująco:

x∼yx=y

x>yx>y

R₊

X

R₊

Relacja słabej preferencji:

czyli

R₊

Ps

Uy X ^I >y ^I

x>y

Ux

Wykład 3

Twierdzenie (wkw ciągłości)

Relacja słabej preferencji jest ciągła przestrzeni X⊂R₊ ⁿ wtedy i tylko wtedy gdy dla każdego koszyka x, zbiory: zbiór koszyków niegorszych niż x S ^≥_x i nielepszych niż S^≤_x są zbiorami domkniętymi.

Przykład nieciągłej relacji preferencji.

X=R²₊

x=(x₁, x₂)∈X y=(y₁, y₂)∈X

Indyferentność

Zatem

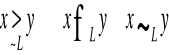
Tak zdefiniowana relacja jest przykładem relacji nieciągłej

Wypukłość relacji

X⊂Rⁿ nazywamy wypukłym ⇔

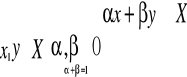
Silnie wypukły wypukły niewypukły

Def

Relację≥ nazywamy wypukła w przestrzeni x jeżeli

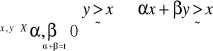
Można pokazać, że relacja słabej preferencji jest wypukła w X w.t.w. gdy zbiór S^≥_x koszyków niegorszych od x jest wypukły dla każdego koszyka x należącego do X.

A b

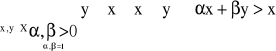
c

Relację ≥ nazywamy silnie wypukłą w przestrzeni x jeżeli

Można dowieść, że jeśli relacja preferencji jest silnie wypukła to zbiór koszyków niegorszych niż x jest silnie wypukły dla każdego koszyka x (typowa sytuacja to b)

X=R²₊

Koszyki optymalne i warunki ich istnienia

(X, ≥)- pole preferencji konsumenta

A⊂X(A≠φ)

Def

Koszyk x^*∈A nazywamy koszykiem optymalnym w zbiorze A jeżeli

Jeżeli relacja preferencji (słabej pref.) jest ciągła w przestrzeni towarów x i zbiór A jest zbiorem zwartym to w zbiorze A istnieje co najmniej jeden optymalny koszyk
towarów. Zbiór wszystkich koszyków optymalnych jest zwartym koszykiem zbioru A.

Zbiór A⊂Rⁿ nazywamy zwartym,gdy jest domknięty i ograniczony.

Jeżeli relacja preferencji jest ciągła i słabo wypukła w wypukłej przestrzeni towarów x a zbiór A jest zwarty i wypukły to w zbiorze A istnieje co najmniej jeden koszyk optymalny. Zbiór wszystkich koszyków optymalnych jest w tym przypadku zwartym i wypukłym podzbiorem zbioru A.

Jeżeli relacja słabej preferencji jest ciągłą i silnie wypukła w wypukłej przestrzeni towarów X i zbiór A jest zwarty i wypukły to w zbiorze A istnieje dokładnie jeden optymalny koszyk towarów.

Funkcja użyteczności konsumentów.

U:xR -tak też można opisać

Użyteczność to zdolność dóbr do zaspokojenia potrzeb konsumenta. Aksjomatyczną teorię użyteczności w latach 40 XX w stworzyli J. Von Neumann, O. Morgenstern.

XIIIw teoria gier hazardowych, paradoks petersburski

Def

Funkcję u:XR (x pole preferencji konsumenta)nazywamy funkcją użyteczności konsumenta reprezentującą relację preferencji jeżeli dla każdych dwóch koszyków.

Tak zdefiniowana funkcja użyteczności nazywa się porządkową funkcją użyteczności.

x∈X

u(x)∈R

Liczba zwana użytecznością u(x) bywa czasem interpretowana jako stopień zadowolenia.

Kardynalna interpretacja użyteczności

Tw

Jeżeli funkcja u reprezentuje relację słabej preferencji to dla każdych dwóch koszyków x,y∈X

• U(x)=u(y)x∼y

• U(x)>u(y)xy

Jeżeli funkcja u:XR reprezentuje relację preferencji y:RR jest funkcją rosnącą oraz istnieje funkcja zlożona

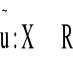
,x∈X to funkcja

też jest funkcją użyteczności reprezentującą relację słabej preferencji

Twierdzenie G. Debreu

Jeżeli przestrzeń towarów X⊂R₊ⁿ jest zbiorem:

• Niepustym i domkniętym

• 
  Spójnym

Tak Nie

• Nieograniczonym z góry

(x∈X∧y≥x⇒y∈X)

(y _i ≥x _i) i=1,...n

oraz relacja preferencji jest ciągła w przestrzeni X to istnieje ciągłą funkcja użyteczności, która reprezentuje tą relację.

Prawdziwe jest też twierdzenie w pewnym sensie odwrotne:

Jeżeli funkcja u:XR jest ciągła w przestrzeni towarów X spełniającej warunki 1-3 to relacja preferencji p= {(x,y)∈X*X\u(x)≥u(y)} też jest ciągła w przestrzeni towarów X.

Przyjmujemy że X=Rⁿ₊ rozważane funkcje będą:

1.Wklęsłe lub silnie wklęsłe (w. Zb. X=Rⁿ₊)

Rⁿ R jest wklęsła w zbiorze wypukłym A w.t.w.

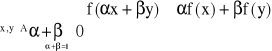
Funkcja jest silnie wklęsła w zb A w.t.w.

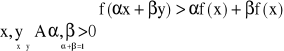
A A A

Wklęsła silnie wklęsła

2. Rosnące w X∈Rⁿ₊

3.Pochodne cząstkowe II rzędu funkcji użyteczności istnieją i są ciągłe w zbiorze Rⁿ₊₊

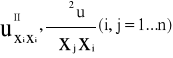
u∈c² (Rⁿ₊₊)

Wykład 4

Tw

Jeżeli funkcja użyteczności u: Rⁿ₊R jest wklęsła (silnie wklęsła)w zbiorze R_n+ to relacja preferencji wyznaczona przez tą funkcję jest wypukła (silnie wypukła)

Gdy f użyteczności jest silnie wklęsła to zbiór:

I

Są silnie wypukłe dla każdego koszyka x.

Przykłady funkcji użyteczności

• Funkcja multiplikatywna (Cobba-Douglasa)

Gdzie 0<α_i<1 x_i>0 (i=1,...n)a>0

• Funkcja addytywna

A_i>0 x_i>0 (i=1,2,...n)

• Funkcja logarytmiczna

A_i>0 x_i>0 (i=1,2..n)

• Funkcja liniowa

(a_i>0)

• Funkcja Leontiefa-Koopmansa

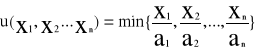
(a_i>0)

Preferencje typu Cobba-Douglasa

Charakterystyki użyteczności:

-Rachunek marginalny-

krańcowa użyteczność, krańcowa stopa substytucji, elastyczność substytucji towarów.

Zakładamy że funkcja użyteczności jest różniczkowalna, silnie wklęsła lub wklęsła, rosnąca.

Dowolny ustalony stopień towarów

Def1

Krańcową użytecznością i-tego towaru w koszyku x nazywamy pochodną cząstkową funkcji użyteczności względem zmiennej x_i czyli:

(i=1,...n)

Jeżeli u jest rosnąca to krańcowa użyteczność każdego towaru jest rosnąca- oznacza to, że zwiększenie ilości jednego towaru w koszyku przy niezmienionych innych zwiększa użyteczność koszyka.

Jeśli jest podwójnie różniczkowalna i silnie wklęsła to:

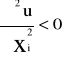
Tzn. krańcowa użyteczność każdego towaru maleje w miarę wzrostu jego spożycia. Zasady malejącej krańcowej użyteczności (prawo Gossena)

Def2

Krańcową stopą substytucji i-tego towaru przez j-ty towar w koszyku x, nazywamy wyrażenie

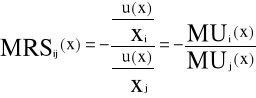
(i≠j)

Mówi o ile (w przybliżeniu) powinna zmniejszyć się ilość j-tego towaru , przy zwiększeniu ilości i-tego towaru o jednostkę aby użyteczność koszyka x pozostała bez zmian.

Def3

Elastycznością substytucji i-tego towaru przez j-ty towar w koszyku x, nazywamy wyrażenie:

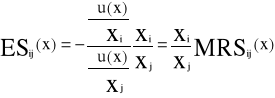
(i≠j)

Pokazuje o ile procent (w przybliżeniu) powinna zmniejszyć się ilość j-tego towaru przy zwiększeniu ilości i-tego towaru o 1% żeby użyteczność koszyka nie zmieniła się.

Maksymalizacja użyteczności konsumpcji. Funkcja popytu konsumenta.

I-dochód konsumenta (budżet konsumenta)

Zbiór budżetowy

D(p, I)={x∈X|<p, x> ≤I}

Czyli zbiór koszyków, na które stać konsumenta. Zbiór D jest zwarty(ograniczony) oraz wypukły

Linią budżetową , nazywamy zbiór

L(p, I)={x∈X| <p, x> =I}

Konsument chce kupić najlepszy koszyk x∈D(p, I)- najlepszy na jaki go stać- optymalny

Jeżeli relacja preferencji jest ciągła i silnie wypukła w przestrzeni towarów X=Rⁿ₊ to dla każdej pary (p, I) istnieje dokładnie jeden koszyk optymalny w zbiorze D(p, I)

Funkcja popytu konsumenta

Maksymalizacja funkcji konsumpcji

Problem

Wyznaczyć maksimum funkcji użyteczności

U(x)max (1)

Przy ograniczeniach <p,x> ≤1 (2)

x≥0 (3)

Jeżeli u spełnia : jest silnie wklęsła, podwójnie różniczkowalna i .........to funkcja popytu

Przy przyjętych założeniach funkcja popytu konsumenta jest funkcją ciągłą. Dla każdego p>0 i I>0 oraz k>0 zachodzi równość

Wtedy γ jest funkcją dodatnio jednorodną stopnia zerowego.

Tw

Jeżeli u jest silnie wklęsła, rosnąca i różniczkowalna w X=Rⁿ₊ oraz konsument musi kupić z n towarów (czyli x>0) to dla każdego wektora cen p>0 i każdego dochodu I>0 istnieje dokładnie jedno rozwiązanie optymalne x* problemu (1)(2)(3). Rozwiązanie to spełnia układ n+1 równań.

Z n+1 niewiadomymi: λⁿ oraz x₁^*, x₂^*...x _n^*

Układ równań (1^I),(2^I) można zapisać w postaci:

.........................................

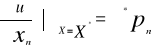
Warunek (1) oznacza, że

Grad u(x*)=λ*

Gdzie

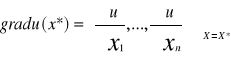
Gradient wskazuje kierunek najszybszego wzrostu funkcji użyteczności u.

Równość (2) oznacza, że koszyk optymalny x* leży na lini budżetowej L(p,I)

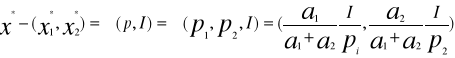
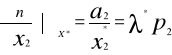
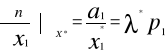
U(x₁, x₂)=a₁ ln x₁+ a₂ ln x₂max

P₁x₁ + p₂x₂ ≤ I

Wykład 5

Def

Macierz

O elementach

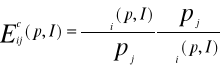
Nazywamy macierzą współczynników elastyczności cenowej popytu w szczególności:

(i=1,...n)

Nazywają się elastycznościami cenowymi popytu

Nazywają się elastycznościami krzyżowymi popytu. E_ii^c pokazuje o ile procent zmieni się popyt na i-ty towar przy wzroście jego ceny o 1%.

E_ij^c pokazuje o ile procent zmieni się popyt na i-ty towar przy wzroście ceny j-tego towaru.

Def

Wyrażenie

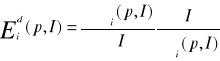
Gdzie i=1,...n nazywa się elatycznością dochodową popytu na i-ty towar

• Towary normalne E^c_ii <0

• Towary Giffena E^c_ii >0

• Towary wyższego rzędu E^d_i >0

• Towary niższego rzędu E^d_i <0

Temat: Elementy teorii produkcji

Producent towarów

Towar:jako towar konsumpcyjny albo czynnik produkcji lub nakład

Proces prod. Przekształcenie (funkcja, transformacja) jednego koszyka towarów w drugi koszyk towarów .

n- liczba towarów na rynku

x-wektor nakładów

y- wektor wyników

x=(x₁,x₂,...x_i...x _n) y=(y₁,y₂,...y_i...y_n)

Będą nas interesowały technologicznie dopuszczalne procesy produkcji, czyli procesy dopuszczalne z technologicznego pkt. Widzenia.

Przestrzeń produkcyjna

Zbiór

Wszystkich technologicznie dopuszczalnych procesów prod (x,y) z normą

Będziemy nazywali przestrzenią produkcyjną

• 
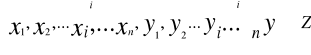
  Pierwsza sytuacja

I-ty towar może być jednocześnie nakładem i wynikiem-jednocześnie zużywany i wytwarzany np. elektrownia x_i>0, y_i>0

• Druga sytuacja

I-ty towar jest wyłącznie zużywany x_i>0, y_i=0

• Trzecia sytuacja

I-ty towar jest wyłącznie wytwarzany x_i=0 y_i>0

Prawa produkcji

I Prawo proporcjonalnych przychodów

Gdzie

Lub inaczej

α
-krotne zwiększenie nakładów powoduje α-krotne zwiększenie wyników.

1^I MALEJĄCE PRZYCHODY

a)

b)

1^II ROSNĄCE PRZYCHODY Prawa alternatywne

a)

b)

Malejące przychody rosnące przychody

II Addytywność dopuszczalnych procesów produkcji

(x,y)∈z∧ (x^I ,y^I)∈z⇒(x+x^I, y+y^I)∈z

III Brak „rogu obfitości”

(θ,y)∈z⇒y=θ z niczego się nic nie produkuje

IV Nieodwracalność procesu produkcji

(x,y)∈z∧x≠y⇒(y,x)∉z

V Możliwość marnotrawstwa

5.1 (x,y) ∈z ∧ θ ≤ y^I ≤ y ⇒ (x, y^I) ∈z

5.2 (x,y) ∈z ∧ x ^I ≥x ⇒(x ^I, y) ∈z

5.1 po stronie wyników

5.2 po stronie nakładów

VI Domkniętość przestrzeni produkcyjnej

Gdy przestrzeń prod spełnia założenia I i II to jest ona stosunkiem wypukłym o wierzchołku w przedziale θ=R²ⁿ₊

Funkcja produkcji

Zakładamy że z jest przestrzenią prod

Przekształceniem technologicznym nazywamy odwzorowanie typu:

Które każdemu wektorowi nakładów x∈Rⁿ₊ przyporządkowuje zbiór wszystkich wyników y∈Rⁿ₊ które można otrzymać dysponując nakładami x z wektora x.

α-multifunkcja

y=x

αx

x

Funkcja prod- def

Proces produkcji (x,y) ∈z nazywamy technologicznie efektywnym jeżeli nie istnieje proces produkcji (x,y^I) ∈z taki że :

Definicja

Jeżeli istnieje funkcja f: Rⁿ₊Rⁿ₊ taka że y=f(x) wtedy i tylko wtedy gdy proces (x,y) ∈z jest technologicznie efektywny, to funkcję f nazywamy wektorową funkcją produkcji związaną z przestrzenia prod z.

W szczególnym przypadku gdy producent wytwarza tylko jeden produkt zużywając w tym celu k-wymiarowy (k≤n) wektor nakładów funkcja produkcji jest typu f: R^k₊ R₊ i nazywamy ją wtedy skalarną k-czynnikową funkcją produkcji

Y₀

X₀

Założenie: (k-czynnikowej skalarnej funkcji produkcji)

1. f(Θ)=0

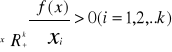
krańcowa wydajność i-tego czynnika zwiększa produkcję.Zwiększenie któregokolwiek z nakładów powoduje wzrost prod.

3.f-funkcja wklęsła

4.

f-funkcja jednorodna stopnia r

gdy r>1 w procesie produkcji występują „korzyści wielkiej skali”

gdy 0≤r<1 w procesie produkcji występują „niekorzyści wielkiej skali”

I

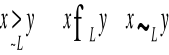
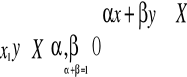
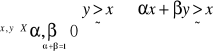
Kx

Kx

Kx

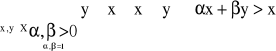
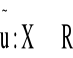
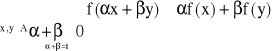
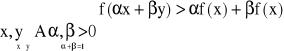
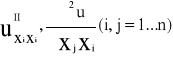
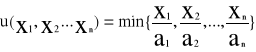
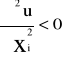
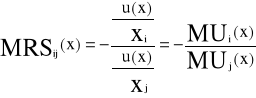
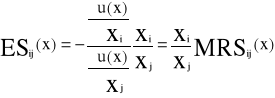
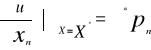
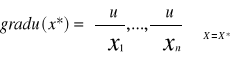
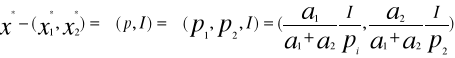
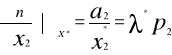
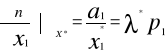
GradI(x*)

D(P,I)

L(P,I)

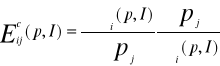
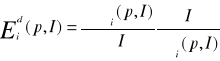
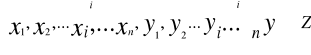
Z

Z

(y,x)∉Z

Y=x

Z

Z

Z

(x₀,y₀)

Z

---