ANALIZA NIEPEWNOŚCI POMIAROWYCH

Na podstawie strony przygotowanej z książki: "Teoria pomiarów", pod redakcją Henryka Szydłowskiego, PWN 1981. Skrócona wersja tego opracowania znajduje się w nowszych wydaniach skryptu "Ćwiczenia laboratoryjne z fizyki " pod redakcją Tadeusza Rewaja.

1. POMIARY FIZYCZNE I NIEPEWNOŚCI POMIAROWE

1.1. Niepewności systematyczne (błędy systematyczne)

1.2. Niepewności przypadkowe (błędy przypadkowe)

1.3. Podsumowanie

2. NIEPEWNOŚCI SYSTEMATYCZNE

2.1. Niepewności systematyczne pomiarów bezpośrednich

2.2. Niepewności systematyczne pomiarów pośrednich

2.3. Graficzne przedstawienie niepewności systematycznych

3. NIEPEWNOŚCI PRZYPADKOWE

3.1. Rozkład normalny

3.2. Populacja generalna, próba, estymatory

3.3. Rozkład Studenta, estymacja przedziałowa wartości oczekiwanej

3.4. Niepewność przypadkowa pomiarów pośrednich

3.5. Rozkład prostokątny

4. NIEPEWNOŚCI CAŁKOWITE

4.1. Pomiary bezpośrednie

4.2. Pomiary pośrednie

5. GRAFICZNA ANALIZA DANYCH POMIAROWYCH

5.1. Zasady sporządzenia wykresów

5.2. Regresja liniowa

1. Transformacja niektórych funkcji nieliniowych do postaci liniowej

1. PYTANIA I ZADANIA

2. TABELE

1. Pomiary fizyczne i niepewności pomiarowe

Załóżmy, że pewna mierzona wielkość fizyczna x (np. długość, czas, masa, prędkość) ma rzeczywistą wartość
, której z reguły nie znamy. W wyniku pomiaru tej wielkości nie uzyskujemy zasadniczo jej rzeczywistej wartości. Składa się na to wiele powodów, zależnych od metody pomiaru, użytych przyrządów pomiarowych, obserwatora, itp. Mówimy, że każdy pomiar obarczony jest niepewnościami (lub błędami pomiarowymi) pomiarowymi.

Występują dwa zasadnicze rodzaje niepewności pomiarowych:

• niepewności systematyczne

• niepewności przypadkowe.

Zwykle w każdym pomiarze występują one łącznie, składając się na niepewność całkowitą. Poniżej omówimy pokrótce oba rodzaje niepewności, które później zostaną przedstawione bardziej szczegółowo.

1.1. NIEPEWNOŚCI SYSTEMATYCZNE

A. W jaki sposób się objawiają ?

a) Wyniki kilkakrotnie powtarzanego pomiaru są identyczne

B. Jaka jest tego przyczyna ?

a) Użyty przyrząd pomiarowy nie pozwala na uzyskanie większej dokładności (ograniczona liczba kresek podziałki przyrządu, klasa miernika).

b) Obserwator ma ograniczoną dokładność odczytu.

Komentarze do powyższych punktów:

1.1.A.a: Powtarzanie pomiarów ma sens tylko wtedy, gdy powtarza się od początku wszystkie czynności prowadzące do uzyskania rezultatu liczbowego. Na przykład mierząc suwmiarką średnicę walca za każdym razem wybiera się na nowo miejsce pomiaru średnicy, na nowo dociska suwmiarkę itp. Powinno się zmieniać na nowo jak największą liczbę czynników wpływających na wynik pomiaru (osoba wykonująca pomiary, przyrząd pomiarowy, data wykonania pomiaru itp.). Jeżeli tak zrobione pomiary dają identyczne wyniki, to ich wielokrotne powtarzanie nie zwiększa dokładności rezultatu końcowego.

1.1.B.a: Przyrządy pomiarowe budowane są w taki sposób, aby wyniki pomiarów wielkości x nie różniły się od wartości rzeczywistej xp więcej niż o wartość najmniejszej działki na przyrządzie dx. Wartość rzeczywista mieści się zatem w przedziale (x - dx, x + dx). Dokładność dx stanowi maksymalną wartość niepewności systematycznej wnoszonej przez sam przyrząd i dlatego dx nazywana jest często niepewnością maksymalną. Oto przykładowe niepewności systematyczne dla kilku przyrządów pomiarowych:

linijka milimetrowa
.

sekundomierz
.

termometr pokojowy T = 1 ^oC.

Działki elementarne na niektórych miernikach są tak duże, że istnieje możliwość odczytu z większą dokładnością, ale mimo tego jako niepewność systematyczną przyjmujemy wartość równą działce elementarnej. Precyzja odczytu może być większa, gdy interesują nas nie wartości bezwzględne, ale różnice dwóch odczytów.

W przypadku analogowych mierników elektrycznych, różnicę pomiędzy wynikiem pomiaru a wartością rzeczywistą znajdujemy posługując się liczbą zwaną klasą przyrządu. Klasą przyrządu nazywamy wyrażony w procentach stosunek niepewności systematycznej do pełnego zakresu wychylenia miernika. Na przykład, dla amperomierza o klasie 0,5 i maksymalnym zakresie 5 A niepewność systematyczna ΔI jest równa

Dla mierników cyfrowych za niepewność systematyczną przyjmujemy najmniejszą wartość wyświetlaną na danym mierniku.

1.1.B.b: Obserwator wnosi niezależny przyczynek do niepewności systematycznej. Mierząc np. czas trwania jakiegoś procesu musimy uwzględnić skończony czas refleksu obserwatora. Przy pomiarze odległości popełniamy zwykle błąd paralaksy. Wkład obserwatora do niepewności systematycznej jest z reguły mniejszy od dokładności przyrządu pomiarowego.

Przykład 1. Woltomierzem klasy 0,2 o zakresie do 10 V wykonujemy odczyt napięcia na oporniku. Położenie wskazówki woltomierza możemy odczytać z dokładnością do 0,01 V. Jaka jest niepewność systematyczna pomiaru ?

Niepewność wynikająca z klasy przyrządu wynosi 0,02 V a niepewność odczytu 0,01 V. Całkowita niepewność systematyczna pomiaru wynosi więc U = 0,02 + 0,01 = 0,03 V. Gdybyśmy przykładowo odczytali wartość U = 3,05 V, to wynik końcowy zapiszemy w postaci

1.2. NIEPEWNOŚCI PRZYPADKOWE

A. W jaki sposób się objawiają ?

a) Przy kolejnych powtórzeniach pomiaru nie uzyskuje się identycznych wyników, występuje ich statystyczny rozrzut.

B. Jaka jest tego przyczyna ?

a) Brak identyczności elementów zbioru.

b) Niezgodność przyjętego modelu z obiektem mierzonym.

c) Metoda pomiaru, zmienne warunki pomiaru, wpływu zmysłów obserwatora.

Komentarze do powyższych punktów:

1.2.A.a: Zwiększenie ilości pomiarów prowadzi do zmniejszenia niepewności pomiarowej. Wartości pomiarów grupują się w specyficzny sposób wokół wartości rzeczywistej. Gdy wykonujemy bardzo dużo pomiarów, wyniki niektórych z nich mogą być takie same.

1.2.B.a: Ta przyczyna występuje wtedy, gdy pomiary wykonujemy nie na pojedynczym obiekcie, ale na pewnym zbiorze, dla którego zdefiniowana jest mierzona wielkość. Na przykład, mierzymy średnice pewnej liczby metalowych kulek, wykonujemy pomiary modułu Younga na wielu próbkach tego samego materiału itp. Rozrzut wyników wynika ze statystycznego charakteru mierzonej wielkości.

1.2.B.b: Tutaj przyczyną jest odstępstwo przedmiotu pomiaru od założonego modelu. Na przykład, mamy zmierzyć długość walca i zakładamy, że jest to idealny walec. Nie jest to oczywiście prawdą i dlatego pomiar jego długości wzdłuż różnych linii nie da nam tych samych wyników. Odstępstwo przedmiotu od ideału ujawni się wtedy, gdy dokładność stosowanego przyrządu pomiarowego jest wystarczająco duża.

1.2.B.c: Przykładem na to, że metoda pomiarowa wnosi własny przyczynek do niepewności przypadkowej jest pomiar długości gumki. Wynik pomiaru zależy od naprężenia gumki i sposobu przykładania linijki. Również przypadkowo zmieniające się czynniki zewnętrzne (ciśnienie, temperatura) mają wpływ na rezultat końcowy. Wpływ zmysłów na wynik pomiaru występuje najwyraźniej wtedy, gdy musimy ocenić minimum lub maksimum natężenia dźwięku, równości oświetlenia pola widzenia itp.

1.3. PODSUMOWANIE

Celem ustalenia, która z niepewności dominuje, pomiar należy powtórzyć kilkakrotnie, 3-4 razy. Jeżeli wyniki kolejnych pomiarów są identyczne, wtedy miarą dokładności pomiaru są niepewności systematyczne. Jeżeli natomiast występuje statystyczny rozrzut wyników, czyli każdy pomiar daje inny rezultat, lub przynajmniej niektóre wyniki są różne, a różnice pomiędzy poszczególnymi wynikami przewyższają niepewności systematyczne, wtedy dominuje niepewność przypadkowa.

W pomiarach, z którymi mamy do czynienia, występują z reguły niepewności systematyczne jak i przypadkowe. Na początku ograniczymy nasze rozważania do przypadków skrajnych, w których dominuje tylko jeden rodzaj niepewności.

W rozdziale 2 omówimy sposób opracowania wyników pomiarowych obarczonych jedynie niepewnościami systematycznymi, w rozdziale 3 jedynie niepewnościami przypadkowymi, zaś w !!!!!rozdziale 4 przedstawimy sposób na ich połączenie.

2. Niepewności systematyczne

2.1. NIEPEWNOŚCI SYSTEMATYCZNE POMIARÓW BEZPOŚREDNICH

O pomiarze bezpośrednim mówimy wtedy, gdy wartość liczbowa pewnej wielkości odczytana być może bezpośrednio z przyrządu pomiarowego. Do takich pomiarów należy np. odczyt długości ciała za pomocą linijki, odczyt długości czasu trwania spadku ciała za pomocą sekundomierza, odczyt temperatury za pomocą termometru.

W poprzednim paragrafie przedstawiono sposób wyznaczenia niepewności systematycznych dla mierników oraz dodawania ich, gdy występuje kilka źródeł niepewności systematycznych. Często stosowaną wielkością jest niepewność względna pomiaru

gdzie Δx jest niepewnością systematyczną mierzonej wielkości x. Niepewność względna jest niemianowana i często bywa wyrażona w procentach. Nazywa się wówczas niepewnością procentową

.

Przykładowo, gdy stoperem wyznaczyliśmy czas spadania ciała otrzymując t= 12,2 s, a jako niepewność systematyczną przyjmiemy Δt = 0,2 s, to wynik pomiaru zapiszemy

t = (12,2
0,2) s.

Zatem niepewność względna wynosi

a niepewność procentowa

2.1.1. KILKAKROTNE, NIEZALEŻNE POMIARY Z RÓŻNYMI NIEPEWNOŚCIAMI SYSTEMATYCZNYMI

Załóżmy, że czas spadku kuli mierzono raz zegarkiem z sekundnikiem otrzymując

t₁ = (10
1) s, drugim razem stoperem uzyskując t₂=(9,4
0,2) s.

Jak w takim przypadku obliczyć czas spadku kuli i niepewność systematyczną? Ponieważ oba te rezultaty nie przedstawiają tej samej wartości (drugi pomiar jest dokładniejszy), nie mogą one wnosić tego samego wkładu do wyniku końcowego. Wprowadźmy zatem liczby w_i zwane wagami w taki sposób, aby preferować większy wkład dokładniejszych pomiarów. Dla naszego przykładu można przyjąć:

w₁= 1, w₂= 5.

Sama wartość liczb w_i nie jest ważna, ważny jest ich stosunek, który odzwierciedla wielkość niepewności każdego przyrządu. Mamy bowiem

Δt₁ : Δt₂= 1 : 0,2 = 5 :1 = w ₂ : w ₁

Jako wynik końcowy przyjmujemy średnią arytmetyczną ważoną

(2.1)

a jako niepewność systematyczną średniej ważonej przyjmiemy średnią ważoną niepewności poszczególnych pomiarów

(2.2)

Dla naszego przykładu

Rezultat końcowy zapiszemy zatem tak

Podobnie postępujemy, gdy mamy kilka serii pomiarowych o różnych liczebnościach.

Przykład 2. Dwu obserwatorów zmierzyło długość pewnego odcinka, uzyskując następujące wyniki:

Jaka jest długość tego odcinka i jaka jest niepewność systematyczna ?

Większą wagę należy przypisać wynikom pierwszego obserwatora, ponieważ wykonał on więcej pomiarów. Dlatego przyjmujemy

w ₁= 1; w ₂= 0,5 .

Wtedy :

Rezultat końcowy zapiszemy w postaci

2.2. NIEPEWNOŚCI SYSTEMATYCZNE POMIARÓW POŚREDNICH

Załóżmy, że mierzymy wielkości x₁, x₂,…,x_n, a wartość wielkości  z  obliczamy ze wzoru z = f(x₁, x₂,…,x_n). Zatem wielkość z nie jest mierzona bezpośrednio i o takich pomiarach mówimy, że są pomiarami pośrednimi. Przykładowo, mamy za zadanie wyznaczyć prędkość pewnego ciała poruszającego się jednostajnie, dysponując jedynie sekundomierzem i linijką. Wielkościami, które mierzymy są zatem długość odcinka s i czas jego przebycia t. Prędkość ciała wyznaczymy ze wzoru
. Jak wyznaczyć niepewność Δv, która musi być związana z niepewnościami s i t ? Rozważmy ten problem ogólnie. Niech mierzone będą wielkości x₁, x₂,...,x_n i każda z nich obarczona jest niepewnością systematyczną, odpowiednio Δx₁, Δx₂,..., Δx_n. Zakładając, że
(są odpowiednio małe) dla i = 1,2,...,n, posługując się rozwinięciem Taylora otrzymamy

Jeżeli założymy ponadto, że wszystkie Δz_i mają ten sam znak (np. są dodatnie), to Δz obliczone z powyższego wzoru nazwiemy niepewnością maksymalną z_m.

Przykład 3. Zmierzono wymiary geometryczne walca, otrzymując:

Obliczyć objętość V tego walca oraz niepewność ΔV.

Objętość
Maksymalną niepewność systematyczną obliczymy ze wzoru (2.3), otrzymując

Wynik końcowy zapiszemy w postaci

V=(38,2
6,5) cm³

POCHODNA LOGARYTMICZNA

UWAGA! Jeżeli wielkość mierzona opisana jest funkcją w postaci jednomianu (tzn. mówiąc w uproszczeniu - nie występują w niej działania dodawania i odejmowania) można uprościć żmudne obliczanie pochodnych tych funkcji. W tym celu wstępnie logarytmujemy całą funkcję, a dopiero potem różniczkujemy. Jako przykład weźmy zależność

Występującą w liczniku różnicę potraktujmy jako całość tj.
. Teraz wyrażenie

Logarytmujemy

Różniczkujemy

zamieniamy różniczki "d" na przyrosty makroskopowe "Δ" a wszystkie znaki "-" na "+" (błędy mogą się dodawać):

Ostatecznie mamy

Wyrażenie w nawiasie określa tzw. błąd względny - można wyrazić go w procentach. Metoda pozwala "z grubsza" oszacować maksymalny błąd pomiarowy- pozostaje tylko poprawnie określić niepewności poszczególnych wielkości mierzonych.

2.3. GRAFICZNE PRZEDSTAWIENIE NIEPEWNOŚCI SYSTEMATYCZNYCH

Rys.1 Prezentacja graficzna niepewności systematycznych

Załóżmy, że sporządzamy wykres zależności y = f(x). Wartości x_i i y_i otrzymane z pomiarów są obarczone niepewnościami, odpowiednio Δx_i i Δy_i. Oznacza to, że rzeczywiste wartości tych wielkości mieszczą się w przedziałach od y_i - Δy_i do y_i + Δy oraz od x_i - Δx_i do x_i + Δx_i. Przedziały te wyznaczają na płaszczyźnie wykresu prostokąt o bokach 2Δx i 2Δy zwany prostokątem niepewności pomiarowej (patrz rysunek 1), w którym mieści się wartość rzeczywista. Inny sposób przedstawienia niepewności systematycznych pokazano na tym samym rysunku dla punktu o współrzędnych x_j, y_j. Niepewności zaznaczono tam odcinkami o długościach 2Δx_j, 2Δy_j.

3. Niepewności przypadkowe

Niepewności przypadkowe wynikają z równoczesnego działania bardzo wielu niezależnych czynników. Każdy z tych czynników wpływa jedynie nieznacznie na rezultat pomiaru, powodując z prawdopodobieństwem p = 0,5 odchylenie wartości pomiaru o małą wartość w górę lub dół. Sumaryczne działanie wszystkich tych zakłócających czynników jest chaotyczne, dlatego przy powtórnym pomiarze nie otrzymamy tego samego co wcześniej rezultatu. W każdym konkretnym pomiarze nie jest możliwe przewidzenie wielkości i znaku wartości niepewności pomiarowej, ale nie znaczy to, że niepewności nie podlegają żadnym prawom. Prawa te mają charakter statystyczny, tzn. że możemy podać jedynie prawdopodobieństwo wystąpienia wyniku pomiaru. Prawo rozkładu wyników pomiarowych opisuje tzw. rozkład normalny, zwany inaczej rozkładem Gaussa.

3.1. ROZKŁAD NORMALNY N(x_p,σ)

Rozkład ten zawiera tylko dwa parametry: x_p i σ, i jego postać matematyczna jest następująca:

gdzie f jest gęstością prawdopodobieństwa wystąpienia w pomiarze wartości x, µ jest wartością oczekiwaną, a σ odchyleniem standardowym. W kontekście teorii pomiarów f oznacza szansę na wystąpienie wartości x, µ jest pewną rzeczywistą wartością, a σ jest miarą rozrzutu otrzymywanych wartości x, czyli jest miarą niepewności pomiarowej. Prawdopodobieństwo uzyskania wyniku x zawartego w przedziale (x₁, x₂) wynosi .

Jest to krzywa gęstości prawdopodobieństwa f(x) niestandaryzowanego rozkładu normalnego dla µ=1 i σ=0,5

Wykres funkcji f dla µ=1 i σ=0,5 przedstawiony jest na rysunku 2. Widać, że w wyniku pomiarów obarczonych niepewnością przypadkową najczęściej otrzymamy wartości leżące w pobliżu rzeczywistej wartości. Krzywa jest symetryczna wokół wartości x = 1 w punktach odległych o od maksimum na punkty przegięcia. Jak nietrudno to obliczyć,

co oznacza, że prawdopodobieństwo otrzymania rezultatu z tego przedziału jest równe 68,3%.

Podana powyżej postać f(x) nosi nazwę niestandaryzowanego rozkładu normalnego. Używa się także standaryzowanej postaci tego rozkładu, wprowadzając zmienną standaryzowaną

Wtedy:

Jest to krzywa gęstości prawdopodobieństwa f(u) standaryzowanego rozkładu normalnego
Wykres tej funkcji przedstawia rysunek:

Jedyna różnica pomiędzy wykresami na powyższych rysunkach polega na przeskalowaniu osi układu współrzędnych.

3.2. POPULACJA GENERALNA, PRÓBA, ESTYMATORY

Dokładne poznanie rozkładu normalnego wymaga wykonania nieskończonej ilości pomiarów, co oczywiście nie jest możliwe. Praktycznie dysponujemy jedynie skończoną, i zwykle niewielką ilością pomiarów. Nazwijmy zespół tych pomiarów próbą. Próba może być duża, np. gdy ilość pomiarów n > 30, jak też i mała 10 < n < 30 , lub bardzo mała n < 10. Termin próba pojawił się dzięki następującej analogii. Wyobraźmy sobie, że pojemnik zawiera nieskończenie wiele kul, zaś na każdej z nich napisany jest wynik pomiaru pewnej wielkości x, obarczony jedynie niepewnością przypadkową, podlegającą rozkładowi normalnemu
. Nazwijmy ten zbiór kul populacją generalną. W tej populacji najwięcej jest oczywiście kul, na których znajdują się liczby bliskie m, zaś kul z wartościami znacznie się różniącymi od m jest dużo mniej. Gdy wykonujemy np. pięciokrotny pomiar tej wielkości x, to jest tak, jakbyśmy pięciokrotnie losowali w sposób zupełnie przypadkowy kule z tej populacji generalnej. Liczby na tych wylosowanych kulach to właśnie wyniki naszych pomiarów. Powstaje pytanie, czy parametry obliczone z tych wartości pomiarowych pozwolą obliczyć odpowiednie parametry populacji generalnej tzn. µ i σ? Parametry obliczone z próby celem uzyskania informacji o populacji generalnej nazywa się estymatorami. Estymatory są tym lepszym przybliżeniem parametrów z populacji, im są obliczone z próby o coraz większej liczebności. Należy podkreślić, że estymatory obliczone z próby, nie są identyczne z parametrami populacji ogólnej i same podlegają prawom statystyki.

Poniżej podamy bez dowodu estymatory dla próby dużej i małej.

Próba duża n > 30

a) Estymatorem wartości oczekiwanej m jest średnia arytmetyczna

b) Estymatorem odchylenia standardowego s jest odchylenie standardowe z próby Sx

Próba mała i bardzo mała n < 30

a) Estymatorem wartości oczekiwanej m jest średnia arytmetyczna

b) Estymatorem odchylenia standardowego s jest odchylenie standardowe dla małej próby

.

W powyższym wzorze tn jest współczynnikiem liczbowym, zależnym od ilości pomiarów n, zwanym wartością krytyczną rozkładu Studenta. Wartości tych współczynników podano w tabeli I, II. Sens fizyczny średniej arytmetycznej z próby jest oczywisty: jest to taka wartość, która najbardziej zbliżona jest do wartości rzeczywistej mierzonej wielkości. Nie twierdzimy, że jest ona dokładnie równa wartości rzeczywistej, bowiem powtórne wykonanie serii pomiarowej da nam z reguły inną wartość średniej arytmetycznej. Wartości średnie różnych prób same podlegają rozkładowi normalnemu z własnym odchyleniem standardowym (patrz dalej ).

Odchylenie standardowe z prób interpretujemy jako miarę niepewności przypadkowej pojedynczego pomiaru. Jest to wielkość inna niż niepewność przypadkowa średniej arytmetycznej, dla której miarą jest odchylenie standardowe średniej arytmetycznej

a) dużej próby n > 30

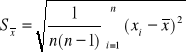
b) dla próby małej i bardzo małej n < 30

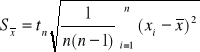
Jak tego należało oczekiwać, te ostatnie odchylenia standardowe
są mniejsze od Sx, ponieważ w średniej niepewności "kasują się", zmniejszając w ten sposób niepewność pomiarową.

Przykład 6. Wykonano n = 8 pomiarów czasu zderzenia dwu metalowych kul i uzyskano następujące wartości (wszystkie w ms): 125, 134, 121, 128, 127, 129, 130, 125. Obliczyć wartość średnią i odchylenie standardowe. Wartość średnia

W tabeli II odczytujemy wartość krytyczną t₈ = 1,0765, a odchylenia standardowe S_t i
obliczymy z powyższych wzorów , otrzymując

Niepewność pomiarowa pojedynczego pomiaru wynosi zatem 4,2 µs, a niepewność średniej arytmetycznej wynosi 1,5 µs. Ostatecznie zapiszemy

3.3. ROZKŁAD STUDENTA, ESTYMACJA PRZEDZIAŁOWA WARTOŚCI OCZEKIWANEJ

Dla prób o małej liczebności stosujemy zamiast rozkładu normalnego rozkład Studenta. Dla dużej próby jest on identyczny z rozkładem Gaussa, dla niewielkich wartości n krzywa Studenta jest bardziej płaska i odległość między punktami przegięcia jest większa niż dla rozkładu normalnego. Rozkład Studenta jest stabelaryzowany, ale zwykle nie interesuje nas ani gęstość prawdopodobieństwa, ani dystrybuanta, lecz tzw. wartości krytyczne
Parametr
, występujący jako wskaźnik przy t, nazywa się poziomem istotności, zaś (1 -
) nosi nazwę poziomu ufności. (Używam także litery a zamiennie, ze zwyczajowo używaną, literą
ze względu na wygodę pisania). Wartości
podane są w tabeli I, II (koniec dokumentu). Zauważmy, że
występujące we wcześniejszych wzorach jest wartością krytyczną
dla
= 0,317.

Sens poziomu istotności (lub poziomu ufności) wynika z poniższego równania

które mówi, że prawdopodobieństwo tego, że wartość Q leży w przedziale (q₁, q₂) jest równe 1 -
. Wartość
przyjmuje się dowolnie, jednakże w pomiarach fizycznych wybiera się ją tak, aby 1 -
było równe lub większe od 0,95. Oznacza to, że będziemy twierdzili coś z prawdopodobieństwem 95 % lub większym. Szerokość przedziału (q₁,q₂) zwanego przedziałem ufności zależy oczywiście od poziomu ufności. Im wyższy poziom ufności, tym szerszy przedział ufności.

Stosując rozkład Studenta, można udowodnić, że

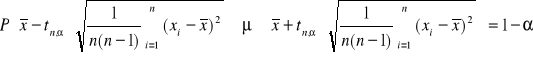
Jest to bardzo ważne równanie, bowiem pozwala wnioskować o nieznanej rzeczywistej wartości (µ) z obliczonej średniej arytmetycznej
.

Przykład 7. Posługując się danymi z przykładu 6, podać przedział ufności dla

1 -
= 0,98.

Z tabeli II odczytujemy wartość krytyczną t_8;0,02 = 2,998. Wyrażenie:

ma wartość równą

Stąd

Oznacza to, że nieznana wartość oczekiwana (czyli rzeczywista wartość czasu zderzenia kul)znajduje się z prawdopodobieństwem 98 % w przedziale (jest nakryta przedziałem):

.

3.4. NIEPEWNOŚĆ PRZYPADKOWA POMIARÓW POŚREDNICH

W praktyce laboratoryjnej jest to sytuacja najczęściej spotykana, gdy mierzona wielkość z jest funkcją innych zmiennych

i mierzy się bezpośrednio jedynie x₁, x₂,...,x_n. Dla każdej z tych bezpośrednio mierzonej wielkości x_i możemy obliczyć wartość średnią
i odchylenie standardowe
. Okazuje się, że wartość średnia
jest równa

Jakie jest odchylenie standardowe
 tej wielkości ? Można pokazać, że

Jest to tzw. prawo przenoszenia odchyleń standardowych.

Przykład 8. W celu wyznaczenia momentu bezwładności cienkiej tarczy zmierzono jej masę i średnicę, otrzymując

Obliczyć moment bezwładności tej tarczy i niepewność pomiarową.

Moment bezwładności tarczy względem osi przechodzącej przez jej środek i prostopadłej do jej płaszczyzny podaje wzór

Zatem

Niepewność pomiarową tej wielkości obliczymy korzystając z prawa przenoszenia odchyleń standardowych. W tym celu obliczmy najpierw składniki występujące w sumie pod pierwiastkiem

Zatem

Zgodnie z probabilistyczną interpretacją odchylenia standardowego, w przedziale
będzie leżało 68,3 % uzyskanych wyników pomiarów.

3.5. ROZKŁAD PROSTOKĄTNY

Rozkład ten odgrywa bardzo ważną rolę przy analizie niepewności systematycznych. Opisuje on taki proces, w którym wypadnięcie wartości z pewnego przedziału (a, b) jest tak samo prawdopodobne, a prawdopodobieństwo wartości spoza tego przedziału jest równe zeru (rysunek 4). Wyniki pomiarów obarczonych niepewnością systematyczną  (Δx) można przybliżyć rozkładem prostokątnym, dla którego b - a = 2Δx. Można udowodnić, że pomiędzy odchyleniem standardowym Sx a niepewnością systematyczną Δx istnieje następujący związek

.

Przykład 9: Obliczyć odchylenie standardowe pomiaru wykonanego za pomocą woltomierza o klasie 0,5 , mającego na skali maksymalną wartość

U = 50 V.

Obliczymy najpierw niepewność systematyczną ΔU

.

Następnie, korzystając z powyższego wzoru otrzymamy

Równanie to jest ważne dlatego, że umożliwia zamianę niepewności systematycznych na wielkość stosowaną dla niepewności przypadkowych, co umożliwia jednolite traktowanie obu tych różnych typów niepewności.

4. Niepewności całkowite

Dotąd zajmowaliśmy się wyłącznie dwoma skrajnymi przypadkami, w których bądź to dominowały niepewności systematyczne, bądź też niepewności przypadkowe. Rzeczywiste pomiary nie mieszczą się w tych dwóch skrajnych kategoriach, wobec czego należy zastanowić się, jak postępować w przypadkach pośrednich, w których obydwa rodzaje niepewności są tego samego rzędu.

4.1. POMIARY BEZPOŚREDNIE

Jeżeli wielkość mierzona x obarczona jest kilkoma niepewnościami systematycznymi
dla r =1,2,...,R, to zamieniamy je na odchylenie standardowe zgodnie ze wzorem

(w)

a następnie obliczamy sumaryczne odchylenie standardowe związane z niepewnością systematyczną:

Dalej musimy uwzględnić niepewność przypadkową, której miarą będzie odchylenie standardowe dane równaniem (3.8) lub (3.9), otrzymując odchylenie standardowe całkowite

Przykład 10. Ocenić niepewność pomiaru wykonanego 5-krotnie sekundomierzem o dokładności Δ₁t = 0,1 s, w którym uzyskano wyniki: 6,7; 6,5; 6,8; 6.6; 6,7. Eksperymentator ocenił niepewność systematyczną wiązaną z wyborem chwili włączenia i wyłączenia sekundomierza na Δ₂t = 0,2 s oraz dokładność odczytu Δ₃t= 0,1 s.

Na niepewność całkowitą składają się niepewność przypadkowa ΔS oraz 3 niepewności systematyczne Δ₁t, Δ₂t i Δ₃t. Jako niepewność przypadkową przyjmiemy odchylenie standardowe dla małej próby (n = 5), uzyskując

Niepewność całkowitą obliczamy korzystając z powyższego wzoru, otrzymując

Ostatecznie:

,
.

4.2. POMIARY POŚREDNIE

Chcemy wyznaczyć wielkość z i jej niepewność, mierzymy bezpośrednio
. Każda z wielkości x_i obarczona jest niepewnościami systematycznymi Δ_rx_i oraz niepewnością przypadkową, której miarą jest odchylenie standardowe
. Najbliższą rzeczywistej wartości mz będzie wartość
obliczona ze wzoru

gdzie
są średnimi arytmetycznymi odpowiednich wielkości x_i.

Miarą niepewności pomiarowej będzie odchylenie standardowe
, które obliczamy w ten sposób, że najpierw zamieniamy niepewności systematyczne Δ _rx_i na odchylenia standardowe, a potem stosujemy prawo przenoszenia odchyleń standardowych. W rezultacie otrzymamy

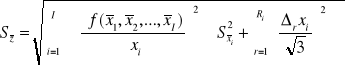
Przykład 11: Celem wyznaczenia przyspieszenia ziemskiego przeprowadzono pomiary czasu spadku ciała z pewnej wysokości. Wysokość spadku h zmierzono 6 razy linijką z podziałką milimetrową, uzyskując następujące wyniki (w mm)

h₁ = 127; h₂ = 126; h₃ = 127; h₄ = 128; h₅ = 128; h₆ = 127.

Czas spadku zmierzono 5-cio krotnie, otrzymując (w s)

t₁ = 0,509; t₂ = 0,511; t₃ = 0,507; t₄ = 0,508; t₅ = 0,509.

Dokładność linijki Δ₁h =1 mm, dokładność odczytu Δ ₂h = 1 mm, niepewność systematyczna związana z ustawieniem linijki Δ ₃h = 1 mm. Dokładność czasomierza Δ ₁t = 0,001 s, niepewność systematyczna związana z wyborem chwili i wyłączenia i wyłączenia Δ ₂t = 0,03 s. Obliczyć z tych danych przyspieszenie ziemskie i jego niepewność.

Przyspieszenie ziemskie będzie można obliczyć z następującego wzoru

Wartość g obliczymy podstawiając do powyższego równania średnie arytmetyczne

wysokości spadku
i czasu spadku
. Dla danych z tego przykładu

Stąd

Miarą niepewności pomiarowej tej wartości
będzie odchylenie standardowe obliczone ze wzoru . Obliczmy najpierw pochodne cząstkowe:

W powyższym wzorze

są odchyleniami standardowymi związanymi z niepewnościami przypadkowymi.

Podstawiając wartości liczbowe do wzoru (4.3) otrzymujemy

Jak to łatwo spostrzec, niepewności związane z pomiarem czasu mają główny wpływ na
.Wynik końcowy zapiszemy w postaci:

,

5. Graficzna analiza danych pomiarowych

Graficzna analiza danych pomiarowych charakteryzuje się względną prostotą i poglądowością. Służy ona do rozwiązywania różnorodnych problemów: znajdywania wartości wielkości fizycznych (interpolacja i ekstrapolacja graficzna), szukania zależności funkcyjnej pomiędzy dwoma wielkościami, znajdywania wartości różnych parametrów, porównywania danych doświadczalnych z teorią itp. Wykres umożliwia rozpoznanie pomyłek eksperymentalnych, dlatego byłoby wskazane sporządzać prowizoryczny wykres już podczas wykonywania pomiarów.

5.1. ZASADY SPORZĄDZANIA WYKRESÓW

Podczas robienia wykresu należy kierować się następującymi zasadami:

1. Wykres wykonuje się na papierze milimetrowym lub na papierze z naniesioną specjalną siatką linii. Rozmiar wykresu określa zakres mierzonych wielkości i wybrana skala na osiach (a nie odwrotnie!).

2. Na osi y odkładamy wartości funkcji, na osi x - wartości argumentów. Na przykład mając wykreślić temperaturową zależność oporu metalu, na osi x odkładamy temperaturę, na osi y - opór elektryczny.

3. Na każdej z osi odkładamy tylko taki zakres zmian mierzonej wielkości fizycznej, w którym zostały wykonane pomiary. Nie ma zatem obowiązku odkładania na osiach punktów zerowych, gdy nie było w ich okolicy punktów pomiarowych.

4. Rozmiar wykresu nie jest dowolny i nie powinien wynikać z tego, że dysponujemy takim a nie innym kawałkiem papieru. Rozmiar powinien być określony przez niepewności pomiarowe tych wielkości, które odkłada się na osiach. Niepewność ta powinna w wybranej skali być odcinkiem o łatwo zauważalnej, znaczącej długości. Na przykład, wykonując pomiar oporu elektrycznego w funkcji temperatury mamy:

Δt = 1 ^oC , ΔR = 1W. Wtedy Δt = 1 ^oC powinien odpowiadać odcinkowi np. 2 mm, ΔR = 1W również 2 mm.

5. Skalę na każdej z osi wybiera się niezależnie, tak że mogą one być różne. Dążymy do tego, aby uzyskany wykres lub jego główna część był pod kątem około 45^o do osi układu współrzędnych.

6. Skalę na osiach układu nanosimy zazwyczaj w postaci równooddalonych, pełnych liczb. Ich wybór i gęstość na osi musi zapewniać jak największą prostotę i wygodę korzystania z nich.

7. Punkty na wykres nanosimy tak, by były wyraźnie widoczne. Gdy na jednym rysunku ma być kilka krzywych, punkty na każdej z nich zaznacza się inaczej: kółkami, trójkątami, kwadracikami itp.

8. Po naniesieniu punktów na wykres, rysujemy ciągłą, bez nagłych zagięć i załamań, krzywą. Powinna ona leżeć tak, aby ilość punktów po obu jej stronach była taka sama. Nie należy dążyć do tego, aby przechodziła ona przez wszystkie punkty, ponieważ każdy z nich obarczony jest niepewnością.

9. Na osiach wykresu muszą być napisane odkładane wielkości i ich jednostki.

10. Aby wykres jak najlepiej odzwierciedlał zależność dwu wielkości, czasami na osiach odkłada się nie same te wielkości, ale ich funkcje. Rodzaj tych funkcji zależy od konkretnej sytuacji. Na przykład, badając temperaturową zależność oporu elektrycznego półprzewodnika oczekuje się następującej zależności

Gdybyśmy narysowali zależność R = f(T), to trudno byłoby stwierdzić, czy jest to eksponenta czy też nie. Natomiast, gdy odłożymy punkty pomiarowe w układzie współrzędnych

i znajdują się one na prostej, to potwierdzimy tym samym oczekiwaną zależność.

11. Na rysunku należy zaznaczyć niepewności pomiarowe w postaci prostokątów lub odcinków.

12. Każdy rysunek powinien być podpisany. Podpis mówi, co rysunek zawiera, wyjaśnia co reprezentują zaznaczone krzywe.

Rys. 5. Prawidłowo i nieprawidłowo sporządzone rysunki, przedstawiające temperaturową zależność oporu elektrycznego metalu

Powyżej przedstawiono dwa rysunki, sporządzone na podstawie tych samych pomiarów. Pierwszy z nich jest nieprawidłowo zrobiony, niezgodnie z wyżej przedstawionymi wskazówkami. Drugi sporządzono kierując się tymi regułami.

5.2. REGRESJA LINIOWA

Często spotykamy się z taką sytuacją, gdy mierzono dwie wielkości x i y związane są ze sobą równaniem liniowym

tak jest np. w przypadku temperaturowej zależności oporu elektrycznego metali

R = f(T), skręcenia płaszczyzny polaryzacji światła w funkcji stężenia roztworu cukru a = f(s), okresu drgań relaksacyjnych w obwodzie kondensatora i neonówki od pojemności kondensatora T = f(C) itp.

Wykonując pomiary tych dwu wielkości x i y uzyskujemy pary liczb (x_i, y_i) i naszym zadaniem jest znaleźć równanie linii prostej (tzn. parametry a i b w równaniu prostej), najlepiej "pasującej" do nich. Niech równanie to będzie miało postać

a "dopasowanie" zgodnie z metodą najmniejszych kwadratów oznacza, że

gdzie a i b są empirycznymi współczynnikami regresji liniowej.

Jak łatwo zauważyć, wyrażenie w nawiasie w tym równaniu jest odchyleniem punktu eksperymentalnego (liczonym wzdłuż osi y) od odpowiadającej mu wartości wynikającej z równania prostej. Poszukując ekstremum związanego powyższego równania udowadnia się, że

gdzie i = 1,2,3,...,n, czyli n jest ilością par punktów (x_i, y_i).

Na odchylenie standardowe S_a i S_b, będące miarą niepewności pomiarowych współczynników regresji a i b otrzymuje się następujące równania

 

Kryterium tego, jak nasze punkty pomiarowe (x_i,y_i) potwierdzają liniową zależność pomiędzy wielkościami x i y, stanowi wartość tzw. współczynnika korelacji liniowej r. Jego wartość zmienia się w granicach od
1 do 0. Gdy |r| = 1, to dopasowanie jest idealne, wszystkie punkty pomiarowe leżą na prostej. Gdy r = 0, to zależność liniowa pomiędzy x_i i y_i nie istnieje. W pomiarach fizycznych wartość współczynnika korelacji r jest zwykle większa niż 0,98. Wzór na współczynnik korelacji

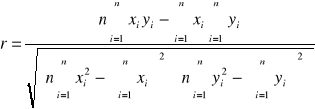
Przykład 11. Wykonując pomiary temperaturowej zależności oporu elektrycznego metalu otrzymano następujące rezultaty:

temperatura [^oC]	19	38	50	65	80
opór [Ω]	150	159	170	175	185

Znaleźć równanie prostej najlepiej pasującej do tych danych oraz współczynnik korelacji.

Wzory, z których będziemy korzystać ( zawierają różne sumy, które obliczymy na początku. U nas x_i to temperatury, a y_i to opory elektryczne, i = 1,2,3,4,5.

Podstawiając te wartości do wzorów (5.3) - (5.7) otrzymamy:

Tak więc nasze x i y spełniają równanie regresji liniowej postaci

y = 0,57 x + 139 lub y = 0,57(4) + 139(2)

Punkty pomiarowe i prosta o tym równaniu zostały pokazane na rysunku 5 , po lewej stronie.

5.3. TRANSFORMACJA NIEKTÓRYCH FUNKCJI NIELINIOWYCH DO POSTACI LINIOWEJ

Regresję liniową można zastosować do tych zależności nieliniowych, które przez odpowiednią transformację zmiennych można zlinearyzować. Rozpatrzmy te, które spotyka się w pracowni studenckiej.

a) równanie typu

gdzie
i a są stałymi, które należy wyznaczyć.

Równanie tego typu opisuje np. zależność amplitudy drgań tłumionych od czasu

,

aktywność próbki promieniotwórczej w czasie

itp.

Sprowadźmy to równanie do postaci liniowej. W tym celu najpierw zlogarytmujmy je stronami

Jeżeli zatem na osi rzędnych odłożymy lny = z , to powyższe równanie będzie równaniem prostej

gdzie
, zaś a = a

b) równanie typu

Z równaniem tego typu spotykamy się, gdy badamy temperaturową zależność oporu elektrycznego półprzewodników
, temperaturowa zależność współczynnika lepkości cieczy
, zależność temperatury wrzenia wody od ciśnienia
itp. Aby sprowadzić takie równanie do postaci liniowej, należy je najpierw zlogarytmować

a następnie dokonać podstawienie

Wówczas otrzymamy

które jest równaniem liniowym, wiążącym t i z.

Zatem sporządzając wykres, należy na osi odciętych odłożyć 1/x a na osi rzędnych lny.

Pytania i zadania

1. Zmierzono pięciokrotnie linijką milimetrową odległość pomiędzy soczewką i ekranem, otrzymując następujące rezultaty (w mm): 138, 139, 138, 139, 139. a) Jaką niepewnością (systematyczną czy przypadkową) obarczone są te pomiary; b) Obliczyć odległość soczewka-ekran, oraz jej niepewność, a także niepewność względną i procentową tego pomiaru.

2. Stoperem, o najmniejszej podziałce 0,1 s wykonano dwa pomiary okresu drgań wahadła matematycznego. W pierwszym pomiarze zmierzono czas 20-tu drgań, otrzymując t₁= 17,2 s. W drugim pomiarze zmierzono czas 30-tu drgań, otrzymując t₂ = 25,4 s. Jaki jest okres drgań tego wahadła i jaka jest niepewność pomiarowa tej wartości ?

3. Z amperomierza o skali do 5 A odczytano natężenie prądu płynącego w obwodzie:
(3,72+ 0,01)A. Jaka jest klasa tego amperomierza ?

4. W ćwiczeniu mającym na celu wyznaczenie parametru χ mierzy się wysokość słupów rtęci h₁ i h₂ na manometrze, a χ oblicza się ze wzoru

W pewnym pomiarze otrzymano h₁ = 152 mm Hg i h₂= 47 mm Hg. Dokładność odczytu wysokości Δh = 1 mm Hg. Obliczyć wartość parametru χ i jego niepewność maksymalną Δχ.

5.Zmierzono pojemność dwu kondensatorów, otrzymując

Jaka będzie pojemność układu tych kondensatorów oraz jej niepewność, gdy te kondensatory połączymy: a) szeregowo, b) równolegle ?

6. Załóżmy, że niepewność przypadkowa jest jedyną niepewnością występującą w pomiarach. a) Jakie jest prawdopodobieństwo uzyskania wyniku pomiaru mieszczącego się w przedziale (m - 2 s, m + 2 s)? b) W jakim przedziale leży 99 % wszystkich pomiarów?

7. Wykonano 5 pomiarów pracy wyjścia elektronu z metalu, otrzymując następujące wartości (w eV): 2,7;2,6; 2,7; 3,1; 2,8. a) Obliczyć wartość średnią i jej odchylenie standardowe. b) W jakim przedziale znajduje się rzeczywista wartość pracy wyjścia, jeżeli przyjmiemy poziom ufności równy 1- α = 0,98?

8. W celu wyznaczenia współczynnika tłumienia drgań tłumionych β zmierzono czas t dziesięciu drgań oraz amplitudę A po tym czasie (przyjmując amplitudę początkową A₀= 1). Uzyskano następujące rezultaty:

Współczynnik tłumienia obliczamy z równania

Obliczyć wartość współczynnika tłumienia i jego niepewność pomiarową.

9. W ćwiczeniu mającym na celu wyznaczenie długości fali świetlnej l za pomocą siatki dyfrakcyjnej o podanej stałej siatki d korzysta się ze wzoru:

gdzie: l - odległość siatki od ekranu, k - rząd ugięcia prążka, x_k- odległość prążka k-tego rzędu od prążka centralnego.

Wyprowadzić wzór na niepewność całkowitą długość fali
, jeżeli wiadomo, że odległość l mierzy się tylko jeden raz i jest ona obarczona niepewnością systematyczną Δ ₁l wynikającą z działki użytego przymiaru i niepewnością systematyczną Δ₂l wynikającą z niedokładnego przyłożenia tej linijki. Jeżeli chodzi o x_k, to dla danego k mierzy się go 5 razy i ponadto obarczone jest także niepewnościami systematycznymi Δ ₁x_k i Δ ₂x_k podobnej natury, co l. Zastosować metodę podaną w rozdziale 4.

10. Jakie wielkości należy odłożyć na osiach układu współrzędnych, jeżeli na rysunku chcemy otrzymać linię prostą w przypadku następujących ćwiczeń:

a) W ćwiczeniu, "Wyznaczanie długości fali światła za pomocą pierścieni Newtona" mierzy się promienie r_k pierścieni k-tego rzędu powstających w wyniku interferencji na warstewce powietrza pomiędzy płaską płytką i płytką sferyczną o promieniu R. Długość fali oblicza się ze wzoru

b) W ćwiczeniu "Badanie fotokomórki gazowej" mierzy się prąd I w obwodzie fotokomórki w funkcji odległość r punktowego źródła światła od fotokomórki. Wiadomo, że natężenie światła od źródła punktowego maleje z kwadratem odległości, a prąd I jest proporcjonalny do natężenia światła.

c) W ćwiczeniu "Badanie drgań tłumionych" mierzy się amplitudę drgań A(t) w chwilach kolejnych maksymalnych, dodatnich wychyleń. Wiadomo, że A(t) = A_oe^-
t.

11. W pręcie, którego jeden koniec jest podgrzewany źródłem o stałej mocy, a drugi koniec jest zanurzony w wodzie z lodem, powstał liniowy gradient temperatury. Oto wyniki pomiaru temperatury T w różnych odległościach x od końca pręta:

x [cm]	10	20	30	40	50
T[^oC]	7,3	16,1	25,0	34,2	43,0

Obliczyć parametry a i b regresji liniowej T = T(x) oraz ich niepewności S_a i S_b, a także współczynnik korelacji.

Tabela I

Wartości krytyczne t_n rozkładu Studenta.(Dla poziomu ufności α = 0,3174)

n	tn	n	tn	n	tn	n	tn
1	-	7	1,0903	13	1,0432	19	1,0284
2	1,8367	8	1,0765	14	1,0398	20	1,0268
3	1,3210	9	1,0663	15	1,0368	21	1,0254
4	1,1966	10	1,0585	16	1,0343	22	1,0242
5	1,1414	11	1,0524	17	1,0320	23	1,0231
6	1,1103	12	1,0474	18	1,0301	24	1,0220

Tabela II

Wartości krytyczne t_n,α rozkładu Studenta

n	α =0,1	α =0,05	α =0,02	α =0,005
2	6,3138	12,7062	31,8205	127,3213
3	2,9200	4,3027	6,9646	14,0890
4	2,3534	3,1824	4,5407	7,4533
5	2,1318	2,7764	3,7469	5,5976
6	2,0150	2,5706	3,3649	4,7733
7	1,9432	2,4469	3,1427	4,3168
8	1,8946	2,3646	2,9980	4,0293
9	1,8595	2,3060	2,8965	3,8325
10	1,8331	2,2622	2,8214	3,6897
15	1,7613	2,1448	2,6245	3,3257
20	1,7291	2,0930	2,5395	3,1737
25	1,7109	2,0639	2,4922	3,0905

1

---