1. def wektora prędkości kątowej i przyśpieszenia kątowego

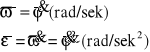
średnia PRĘDKOŚĆ KĄTOWA BRYŁY w przedziale czasu t jest ilorazem przyrostu kąta obrotu tej bryły przez czas, w któ­rym ten przyrost nastąpił

CHWILOWA PRĘDKOŚĆ KĄTOWA BRYŁY jest pochodną względem czasu kąta obrotu tej bryły

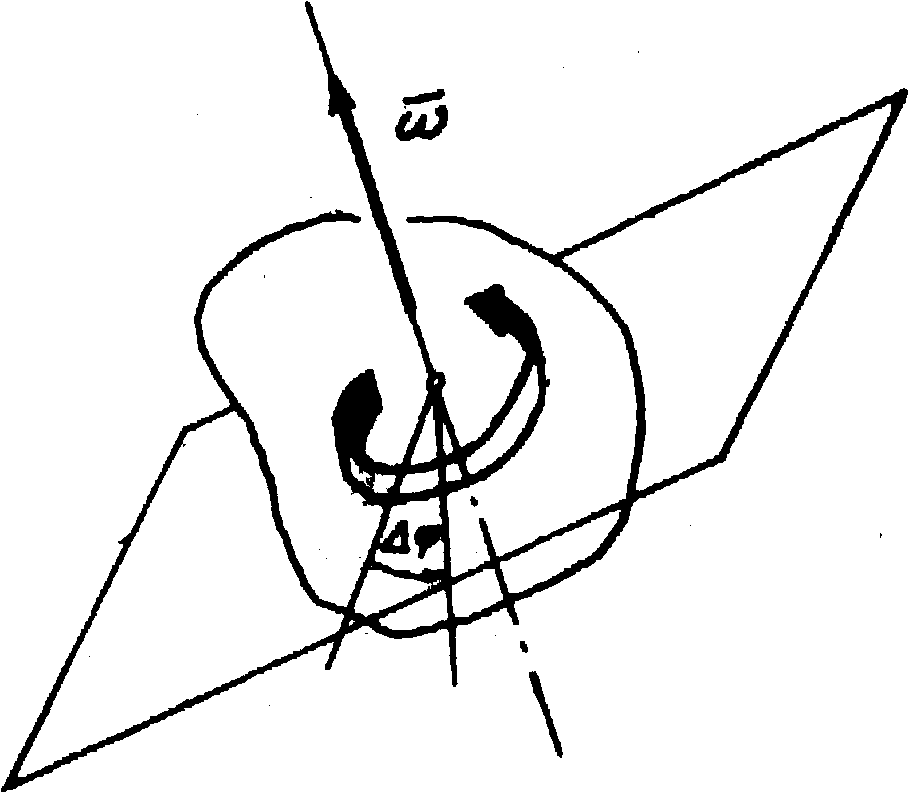
ŚREDNIE PRZYSPIESZENIE KĄTOWE BRYŁY w przedziale czasu t jest ilorazem przyrostu wektora prędkości kątowej tej bryły przez czas w którym ten przyrost nastąpił

CHWILOWE PRZYSPIESZENIE KĄTOWE BRYŁY jest pochodną względem czasu wektora prędkości kątowej

2. PODAĆ I WYJAŚNIĆ NA RYSUNKU TW. KINEMATYKI WYKREŚLNEJ

1. a) Ruty wektorów prędkości pt. leżących na jednej prostej są równe

2. 
   

b) końce wektorów prędkości punktów leżących na jednej prostej muszą leżeć na jednej prostej

3.SZCZEGÓLNE PRZYPADKI RUCHU BRYŁ

Ruch postępowy jest to taki ruch ciała, w którym wektor zwią­zany z tym ciałem nie zmienia swojego kierunku i zwrotu .Wynika stąd, że wektor prędkości kątowej i wektor przy­spieszenia kątowego są =0
4.PRZEŁOŻENIE PRZEKŁADNI ZĘBATEJ O STEŁYCH OSIACH Przekładnia - mechanizm, który zmienia prędkość obrotową jednego wału, na inną prędkość obrotową drugiego wału Przekładnie dzielimy na:

1. Zębate

2. Cierne

3. Pasowe i łańcuchowe

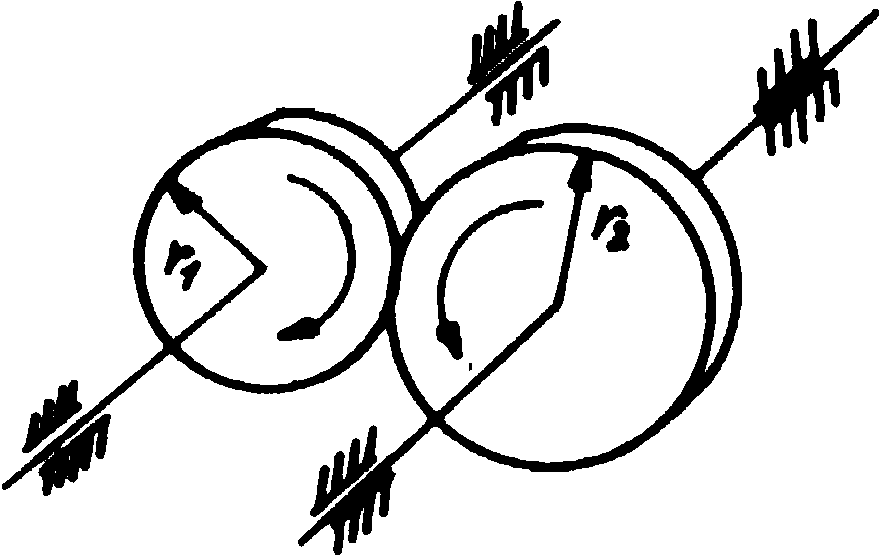
W przekładniach ciernych i pasowych, dla uproszczenia pomijamy po­ślizg między kołami, lub między kołem pasowym i pasem. W przekładniach zębatych operujemy pojęciem średnicy podziałowej .Przełożenie przekładni jest to stosunek prędkości obrotowej wału napędzanego do prędkości obrotowej wału napędzającego.
gdzie n1 i n2 to prędkości obrotowe odpowiednich kół przekładni. Przekładnie zębate i przekładnie cierne zmieniają kierunek prędkości kątowej. Przekładnie pasowe i łańcuchowe nie zmieniają tego kierunku ,z wyjątkiem przypadku, gdy pas jest skrzyżowany

5.METODY OBLICZANIA PR. PUNKTÓW NALEŻĄCYCH DO BRYŁY PORUSZAJĄCEJ SIĘ RUCHEM PŁASKIM

- Metoda analityczna która polega na zróżnicowaniu względem czasu równań ruchu rozpatrywanego punktu

- metoda chwilowego środka obrotu. Chwilowym środkiem obrotu jest punkt o prędkości = 0. Prędkość dowolnego punktu tarczy jest prostopadła do promienia łączącego ten punkt a chwilowym środkiem obrotu

- metoda biegunowa (superpozycji) - prędkość dowolnego punktu A jest równa sumie geometrycznej prędkości V_b bieguna od prędkości w ruchu obrotowym jego punktu A wokół bieguna B

- metoda prędkości obracanych - polega na obracaniu wektorów prędkości o kąt prosty.

- metoda reguły rzutów - rzuty wektorów prędkości dwóch jej dowolnych punktów na prostą łączącą te punkty są sobie równe.

6. Definicja chwil. środka prędkości i przyspieszenia: W ruchu płaskim istnieje taki punkt przynależny do rozpatrywanej bryły, którego prędkość w danej chwili =0, punkt ten nazywamy chwilowym środkiem prędkości. W ruchu płaskim istnieje taki punkt przynależny do rozpatrywanej bryły, którego przyspieszenie w danej chwili czasu jest =0, punkt ten nazywamy chwilowym środkiem przyspieszeń.

7.PRZEKŁADNIA PLANETARNA, OBL JEJ PRZEŁOŻENIE

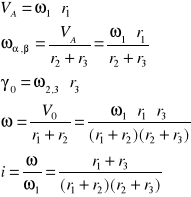
8. PRZYŚPIESZENIE CORIOLISSA

jest równe podwojonemu iloczynowi wektorowemu prędkości kątowej i pr. Względnej

Jest ono wiec prostopadle do wektorów  i W. Jego wartość wynika ze wzoru p₀=2 Wsin gdzie kąt pomiędzy wektorami W i w. Przez punkt p prowadzimy płaszczyznę prostopadłą do osi Z obrotu chwilowego układu U.

Iloczyn wektorowy [_ x W] równy polu utworzonemu z tych 2 wektorów jest w danym przypadku dany [_  W] jest wektorem prostopadłym do tego pola.

9.PRĘDKOŚĆ BEZWZGLĘDNA I PRZYŚPIESZENIE BEZWZGLĘDNE

Prędkością bezwzględną punktu poruszającego się po ruchomej bryle obliczamy z zależności:

gdzie: v_u - pr. unoszenia (pr. punktu bryły, na którym w danej chwili znajduje się rozpatrywany punkt)

v_w - prędkość względna punktu względem bryły, którą myślowo traktujemy jako nieruchomą.

Przyspieszenie bezwzględne punktu poruszającego się po ruchomej bryle obliczamy:

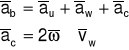
gdzie: a_u - przysp. unoszenia (przysp. punktu należącego do bryły, na którym w danej chwili czasu znajduje się rozpatrywany punkt. a_w - przysp. względne punktu względem bryły, którą myślowo traktujemy jako nieruchomą. a_c - przysp. Coriolisa, gdzie: ၷ jest wektorem prędkości kątowej unoszenia (ciała, względem którego porusza się rozpatrywany punkt).

10. Zasada d'Alemberta dla punktu materialnego.

Siła bezwładności (d'Alemberta) jest to fikcyjna siła, którą wyznaczamy z zależności:

gdzie: m - masa punktu materialnego, a - wektor przyspieszenia tego punktu.

Wypadkowa sił rzeczywistych i fikcyjnych sił bezwładności działających na punkt materialny jest równa zero.

11. Praca stałej siły na prostoliniowym przemieszcze -niu. Jest to iloczyn skalarny wektora tej siły i wektora przesunięcia.

lub z definicji iloczynu skalarnego: W=F*s*cosၡ

względnie:

12. Praca zmiennej siły na krzywoliniowym przemieszczeniu.

Jest to iloczyn skalarny siły przez wektor przesunięcia elementarnego
.

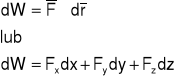
13. Praca i moc pary sił.

Jeżeli do bryły, wykonującej ruch obrotowy przyłożona jest para sił o momencie M to praca elementarna tej pary jest równa:

a praca całkowita podczas obrotu od ၪ₁ do ၪ₂:

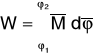
gdzie: M - moment działający na bryłę, dၪ - elementarny obrót bryły, ၪ₁, ၪ₂ - kąty określające położenie bryły na początku i na końcu przedziału czasu, w którym mierzona jest praca W. Jeżeli do bryły, wykonującej ruch obrotowy przyłożona jest para sił o momencie M to moc tej pary jest równa:
gdzie: ၷ - chwil. pr. kątowa

14. Mocy siły.

Moc siły jest to pochodna względem czasu pracy tej siły.

Moc jest iloczynem skalarnym wektora siły i wektora prędkości punktu jej przyłożenia.

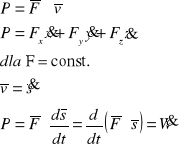
15. MOC PARY SIŁ

W przypadku gdy ciało sztywne porusza się ruchem obrotowym to moc momentu M_z

Jest to iloczyn momentu sił względem osi obrotu przez prędkość kątową.

16.SIŁY POTENCJALNE

Jeżeli praca siły po dowolnym torze jest = 0 taką siłę naz. siłą potencjalną. Siła potencjalna jest siłą ciężkości

17. ENERGIA KINETYCZNA I POTENCJALNA PUNKTU MATERIALNEGO

Energia potencjalna jest to funkcja spełniająca warunek:

V(x, y, z) = - U(x, y, z) + const.

Energia kinetyczna punktu materialnego jest wielkością która = jest połowie iloczynu masy i kwadratu prędkości tego punktu

Energia potencjalna punktu materialnego jest to praca jaką siły pola wykonują przy przemieszczeniu się punktu materialnego z dowolnego punktu do pewnego obranego położenia zerowego. Jest ona równa różnicy potencjałów w dowolnym punkcie zerowym E_p=V-V₀ ; V=-U₁(x₁y₁z₁)+const. W=+U(x₂y₂z₂) - U(x₁y₁z₁) 18. ENERGIA POTENCJALNA SPRĘŻYNY Energia potencjalna sprężyny jest równa pracy jaką wykonuje siła sprężystości przywracająca sprężynę do początkowej długości położenia równowagi x=0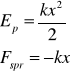

x - oznacza dowolne odkształcenie ciała (wydłużenie lub skrócenie) Siła sprężystości spr

19. Zasada pracy i energii dla punkt materialnego.

Przyrost energii kinetycznej punktu materialnego jest równy sumie prac wszystkich sił na drodze, na której ten przyrost nastąpił.

gdzie: E-E₀ - przyrost energii kinetycznej, W - praca sił.

20. Różniczkowa postać zasady energii

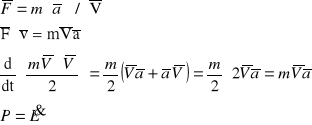
21. Zasada zachowania energii mech. dla punktu materialnego. Energia mechaniczna punktu materialnego jest to suma energii kinetycznej i potencjalnej tego punktu.

Zas. zach .en.mech. - Jeżeli dany układ punktów materialnych porusza się pod działaniem sił potencjalnych to energia mechaniczna tego układu jest wielkością stałą.

E + V = const. gdzie: E - energia kinetyczna, V - energia potencjalna punktu materialnego.

22. Zasada pędu i popędu dla punktu materialnego.

Przyrost pędu punktu materialnego jest równy popędowi sił działających na ten punkt.

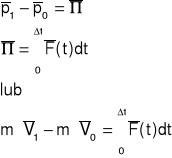
23. Zasada zachowania pędu. Jeżeli popęd sił zewnętrznych działających na punkt materialny jest równy zero to pęd tego punktu nie ulega zmianie.

24.Zasada krętu i pokrętu.

Suma pokrętów sił zewnętrznych względem punktu 0, działających na bryłę jest równa przyrostowi krętu tej bryły.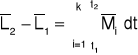

gdzie: L₁ - kręt bryły w chwili czasu t₁, L₂ - kręt w chwili czasu t₂, M_i-moment i-tej siły względem punktu 0, t - czas.

25. Zasada zachowania krętu.

Jeżeli moment sił zewnętrznych działających na bryłę względem punktu 0 jest równy 0, to kręt tej bryły względem punktu 0 nie może się zmienić.

26. Definicja masowego momentu bezwładności względem płaszczyzny.

Jest sumą iloczynów mas elementów tej bryły przez kwadraty odległości tych elementów od płaszczyzny. Masowe momenty bezwładności względem płaszczyzn x-y, y-z, z-x są równe:

gdzie:
- całka po masie bryły.

27. Masowy moment bezwładności względem osi. Jest sumą iloczynów mas elementów tej bryły przez kwadraty odległości tych elementów od osi. Masowe momenty bezwładności bryły względem osi x, y, z sa równe:

gdzie: r_x, r_y, r_z - odległości elementów masy od osi x, y, z.

28. Definicja masowego momentu dewiacyjnego.

Masowy moment dewiacyjny bryły jest sumą iloczynów mas elementów tej bryły przez iloczyny odległości tych elementów od dwóch wzajemnie prostopadłych płaszczyzn. Masowe momenty dewiacyjne względem płaszczyzn układu x, y, z są równe:

Masowy moment bezwładności bryły względem płaszczyzn, z których przynajmniej jedna jest płaszczyzną symetrii, jest równy zero.

35. Definicja głównych osi bezwładności.

Są to trzy wzajemnie prostopadłe osie, tworzące układ względem którego momenty dewiacyjne tej bryły =0

36.Podać def głównych , centralnych momentów bezwładności

Jeżeli: początek układu osi wspólżednych pokrywa się ze środkiem ciężkości figury oraz moment bezwładności = 0 to mamy do czynienia z głównym C.O.B.

37.Jak obliczamy moment bezwładności wzg. Osi nachylonej do osi x,y,z, pod kątem ,,γ

Masowe momenty bezw. bryły względem osi l przechodzą przez punkt 0 i nachylone do osi x,y,z pod kątem ,,γ

I_l=Ixcos²+Iycos²+Izcos²γ-2Dxcos²cosγ-2Dycosγcos  Dzcoscos

38. Podać i objaśnić macierz bezwładności.

Jeżeli znamy moment bezwładności I_x,I_y,Iż, i moment dewiacjny D_x,D_y,D_z, bryły względem dowolnego układu prostokątnego x,y,z to główne momenty bezwładności są równe własnością własnym macierzy bezwładności.

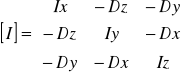
a - cosin. Kierunkowe głównych osi bezwładności są wektorami właściwymi tej macierzy, unormowanymi tak że suma kwadratów ich składowych jest = 0.

39. Definicja macierzy momentów bezwładności.

Jeżeli znamy momenty bezwładności J_x, J_y, J_z i momenty dewiacyjne D_x, D_y, D_z bryły, względem dowolnego układu prostokątnego x, y, z to głowne momenty bezwładności tej bryły sa równe wartościom własnym macierzy bezwładności.

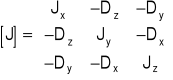
a cosinusy kierunkowe głównych osi bezwładności są wektorami własnymi tej macierzy unormowanymi w ten sposób, że suma kwadratów ich składowych jest równa jednosci.

40. Cosin. Kierunkowe głównych osi bezwładności Cosin kierunkowe osi i- tego (i=1,2,3) głównego mom. bezwładności są równe

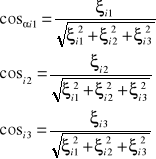
41. Dynamiczne reakcje łożysk wirnika.

Reakcja dynamiczna jest to dodatkowa reakcja więzów wywołana ruchem rozpatrywanego obiektu.

Reakcje dynamiczne łożysk wirnika wirującego względem osi z wyznacza się z następujących równań:

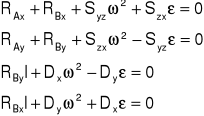
gdzie: ၷ - chwilowa prędkość kątowa wirnika, ၥ - przyspieszenie kątowe wirnika, S_yz, S_zx - masowe momenty statyczne wirnika względem płaszczyzn yz i zx, D_x, D_y - masowe momenty dewiacyjne wirnika względem odpowiednich płaszczyzn układu x, y, z.

42. Warunki statycznego i dynamicznego wyważenia wirników. Warunkiem koniecznym i dostatecznym wyważenia wirnika jest zerowanie się momentów statycznych (warunek wyważenia statycznego) i momentów dewiacyjnych (warunek wyważenia dynamicznego).

Środek masy musi leżeć na osi obrotu oraz oś z musi być jedną z głównych osi bezwładności.

43. Masowy moment dewiacyjny bryły względem płaszczyzn, których przynajmniej jedna jest płaszczyzną symetri = 0.

44.ENERGIA KINETYCZNA W RUCHU POSTĘPOWYM,OBROOTOWYM I PŁASKIM

En. Kin.w ruchu postępowym bryły.

W ruchu postępowym
energia kinetyczna bryły jest równa:

gdzie: m - masa bryły, V_c - prędkość środka masy bryły, która dla ruchu postępowego jest równa prędkości wszystkich punktów należących do bryły.

En. kin. w ruchu obrotowym bryły.

W ruchu obrotowym
energia kinetyczna bryły jest równa:

gdzie: J - masowy moment bezwładności względem osi obrotu, ၷ - prędkość kątowa.

En kin. w ruchu płaskim bryły.

W ruchu płaskim energia kinetyczna bryły jest równa:

+

gdzie: m - masa bryły, V_c - prędkość środka masy, J - masowy moment bezwładności względem osi przechodzącej przez środek masy i prostopadłej do płaszczyzny ruchu, ၷ - prędkość kątowa.

45. Przesunięcie przygotowane (wirtualnego).

Przesunięcie przygotowane
jest to pomyślane (wyobrażalne) przesunięcie punktu, o kierunku zgodnym z kierunkiem możliwej prędkości tego punktu.

Przesunięcie przygotowane jest wektorem, który można przedstawić w następujący sposób:

gdzie: ၤx, ၤy, ၤz - przyrosty elementarne współrzędnych x, y, z.

Jeżeli f(x, y, z) = 0 przedstawia równanie powierzchni, na której znajduje się rozpatrywany punkt (równanie więzów), to dla przesunięcia przygotowanego zachodzi następujący związek:

Przyrosty elementarne współrzędnych prostokątnych dowolnego i-tego punktu są równe:

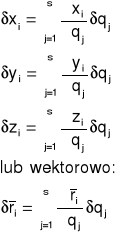
gdzie: s- liczba stopni swobody.

46. Zasada prac przygotowanych.

Praca przygotowana jest to elementarna praca siły
, na przesunięciu przygotowanym
.

Jeżeli układ n punktów materialnych, na który działają siły
, poddano przesunięciom przygotowanym
(i=1,2,...,n) to praca przygotowana tych sił jest równa:

Zasada: Warunkiem koniecznym i wystarczającym równowagi dowolnego ukł. punktów jest, aby suma prac przygotowanych wszystkich sił czynnych i reakcji wię-zów, przy dowolnym przemieszczeniu przygotowanym była równa zero.

gdzie: F_i - siła czynna działająca na i-ty punkt, R_i - reakcja więzów działających na i-ty punkt, ၤr_i - przesunięcie przygotowane i-tego punktu. Zaniedbując tarcie otrzymuj:

47. Co to jest siła uogólniona ? siły uogólnione Q_j(j=1,2,...s) są to wielkości spełniające równanie :

q_j

_{IL- praca przygotow. układu δ}q_j -przesunięcie przygotowane

Q_j - siła uogólniona

S - liczba stopni swobody

48.PODAĆ I OBJAŚNIĆ RÓWNANIA LAGRANGE'A II RODZAJU Równania Lagrange'a II rodzaju mają postać:

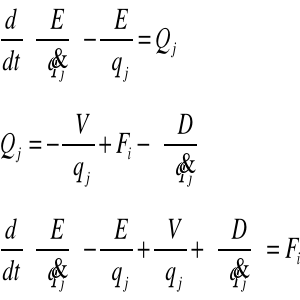
gdzie: E - energia kinetyczna układu, V - energia potencjalna układu, D - funkcja dysypacji energii układu (określa prędkość rozpraszania energii mechanicznej), F_j - niepotencjalna siła, działająca w kierunku j-tej współrzędnej uogólnionej, q_j - j-ta współrzędna uogólniona,
- j-ta prędkość uogólniona, s - liczba stopni swobody, Q_j - siła uogólniona odpowiadająca j-tej współrzędnej uogólnionej.

49.Podać wzór ok reślający siłę uogólnioną w przypadku sił potencjlnych

Siła uogólniona w zachowawczym polu sił:

Q_j= -(δV/δ_qj)*E j=1.2...s

V - en. potencjalna układu, podawana jako funkcja współrz. uogólnionych.

50. Kiedy siła uogólniona ma wymiar [N], a kiedy [Nm]. Siła uogólniona ma wymiar siły , jeżeli odpowiada jej współrzędną jest współrzędna translacyjna (liniowa) oraz wymiar momentu, gdy współrzędna uogólniona jest współrzędną kątową.

---