GEOMETRIA ANALITYCZNA W PRZESTRZENI
ALGEBRA WEKTORÓW
Definicja kartezjańskiego układu współrzędnych:
Kartezjańskim układem współrzędnych prostokątnych (układem ortogonalnym lub ortokartezjańskim) nazywamy uporządkowaną trójkę półosi regularnych wzajemnie do siebie prostopadłych o wspólnym początku i wspólnej jednej długości. Stosujemy oznaczenie OXYZ.
Definicja:
Położenie dowolnego punktu P w przestrzeni można określić za pomocą trójki liczb nazywanych współrzędnymi punktu P, co zapisujemy: P(xp,yp,zp), gdzie:
xp - oznacza współrzędną prostokątną rzutu punktu P na oś OX
yp - oznacza współrzędną prostokątną rzutu punktu P na oś OY
zp - oznacza współrzędną prostokątną rzutu punktu P na oś OZ
Z
zp
P(xp,yp,zp)
yp Y
xp
X
FAKT:
Weźmy punkty A(x1,y1,z1) i B(x2,y2,z2). Punkty te wyznaczają w układzie OXYZ odcinek ![]()
, którego długość wyraża się wzorem:
![]()
Definicja wektora:
Parę uporządkowaną punktów A i B w przestrzeni nazywamy wektorem i oznaczamy symbolem AB lub a, zapisujemy AB=(ax,ay,az), gdzie ax,ay,az nazywamy współrzędnymi wektora AB w układzie OXYZ i obliczamy z zależności:
ax=x2-x1, ay=y2-y1, az=z2-z1
FAKT:
Długość wektora AB, oznaczamy: |AB| lub |a| wyraża się wzorem:
![]()
Przykład: Obliczyć długość wektora rozpiętego między punktami P1(0,2,-1) i P2(3,0,1).
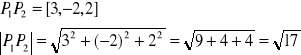
Definicja sumy wektorów:
Sumą wektorów a=[ax,ay,az] i b=[bx,by,bz] nazywamy wektor, którego współrzędne tworzymy dodając odpowiednie składowe wektorów a i b, tj. wektor postaci:
a + b = [ax+bx ; ay+by ; az+bz]
a
a + b
b
b
Własności sumy wektorów:
a+b=b+a (przemienność)
(a+b)+c=a+(b+c) (łączność)
a+0=0+a=a (element neutralny dodawania wektorów)
a+(-a)=0 (wektor przeciwny)
Definicja iloczynu wektora przez liczbę:
Iloczynem wektora (niezerowego) a przez liczbę λ![]()
R, λ![]()
0 nazywamy wektor λa skierowany zgodnie ze skierowaniem wektora a jeśli λ>0, a przeciwnie, jeśli λ<0, o długości równej |λa| w postaci. λa=[ λax, λay, λaz].
Jeśli λ=0 lub a=0 to iloczyn ten jest wektorem zerowym.
Własności iloczynu wektora przez liczbę:
(λ+α)a=λa+αa
λ(αa)=(λα)a
dla α, λ![]()
R
Definicja kombinacji liniowej n wektorów:
Weźmy n wektorów a1, a2,..., an oraz n liczb λ1, λ2,..., λn ![]()
R. Kombinacją liniową wektorów a1, a2,..., an nazywamy wektor postaci:
![]()
Definicja liniowej zależności i niezależności wektorów:
Wektory a1, a2,..., an nazywamy liniowo zależnymi jeśli istnieją liczby λ1, λ2,..., λn nie wszystkie jednocześnie równe zero (tj. ![]()
) takie, że: ![]()
Jeśli wektory a1, a2,..., an nie są liniowo zależne, to są one liniowo niezależne.
Definicja:
Mówimy, że dwa wektory a i b są kolinearne jeśli są liniowo zależne, natomiast trzy wektory a, b i c koplanarne jeśli są one liniowo zależne.
Definicja rzutu prostokątnego punktu:
Rzutem prostokątnym punktu A na oś (skierowaną) S nazywamy punkt A', w którym prostopadła poprowadzona przez punkt A do osi S przecina ją.
A S
.
A'
Definicja rzutu prostokątnego wektora:
Rzutem prostokątnym wektora a=AB na oś (skierowaną) S nazywamy wektor as=A'B', którego początek A' jest rzutem początku wektora a, tj. punktu A, natomiast koniec B' jest rzutem końca wektora a, tj. punktu B.
B
a
A S
B' Oznaczmy przez as długość rzutu wektora a na oś S.
as
A'
α
Twierdzenie:
Długość wektora as będącego rzutem wektora a na oś S jest równa iloczynowi długości wektora a i cosinusa kąta nachylenia wektora a i osi S, tj.: |as|=|a|cos(aS).
Definicja wersora:
Wersorem (lub wektorem jednostkowym) nazywamy wektor o długości jeden.
Definicja wersorów układu współrzędnych:
Wektory i=[1,0,0], j=[0,1,0], k=[0,0,1] nazywamy wersorami odpowiednio osi OX, OY i OZ w układzie kartezjańskim OXYZ.
k 1
j
i 1
1
Definicja:
Współrzędnymi kartezjańskimi prostokątnymi wektora a w przyjętym układzie OXYZ, oznaczonymi przez ax, ay, az, nazywamy współrzędne tego wektora na kolejnych osiach układu.
FAKT:
Dla dowolnego niezerowego wektora a w układzie kartezjańskim zachodzi zależność:
a=[ax, ay, az]
gdzie ax, ay, az oznaczają współrzędne prostokątne wektora w rozważanym układzie.
Piszemy również:
a=axi+ayj+azk
lub
a=ax[1,0,0]+ay[0,1,0]+az[0,0,1]
Definicja kątów kierunkowych:
Kątami kierunkowymi wektora a w układzie kartezjańskim OXYZ nazywamy kąty α, β, γ jakie ten wektor tworzy z kolejnymi osiami układu, tj.:
α=
(a, OX), β=
(a, OY), γ=
(a, OZ)
Cosinusy kątów kierunkowych nazywamy cosinusami kierunkowymi wektora a, przy czym:
![]()
FAKT:
Dla dowolnego wektora niezerowego a cosinusy kierunkowe spełniają następującą zależność:
![]()
Przykład: Wyznaczyć współrzędne wektora a o długości |a|=3 i kątach kierunkowych
![]()
.
Sprawdźmy, czy istnieje wektor a i ![]()
.
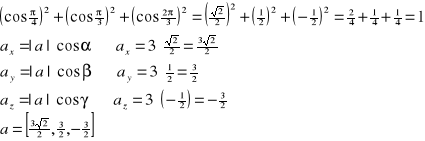
ILOCZYN SKALARNY WEKTORÓW
Niech dane będą wektory niezerowe a=[ax,ay,az] i b=[bx,by,bz].
Definicja iloczynu skalarnego:
Iloczynem skalarnym dwóch wektorów a i b nazywamy liczbę równą iloczynowi długości tych wektorów przez cosinus kąta między tymi wektorami, co zapisujemy:
a![]()
b=|a|∙|b|∙cos
(a, b)
FAKT:
Iloczyn skalarny wektorów a i b równy jest sumie iloczynów odpowiednich wektorów, co zapisujemy:
a![]()
b = axbx + ayby + azbz
Własności iloczynu skalarnego:
a
b=b
a
a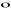
(b+c)=a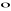
b+a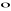
c (rozdzielność względem dodawania)
(αa)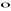
b=a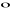
(αb)=α(a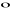
b), α
R
a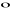
a =|a|2 dla a
0 a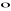
a=0 dla a=0
Przykład: Obliczyć kąt między wektorami:
a=[-1,2,-3] b=[2,0,-1]
a![]()
b=|a|∙|b|∙cos
(a, b) ![]()
cos
(a, b)=![]()
a![]()
b=(-1)∙2+2∙0+(-3)∙(-1)=-2+3=1
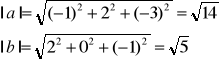
cos
(a, b)=![]()
![]()
(a, b)=arccos![]()
Definicja:
Mówimy, że dwa wektory niezerowe a i b są ortogonalne (prostopadłe), jeśli a![]()
b=0.
WNIOSEK: Dwa wektory niezerowe są prostopadłe wtedy i tylko wtedy, gdy:
axbx+ayby+azbz=0 warunek prostopadłości
natomiast są równoległe, gdy istnieje taka liczba λ![]()
R, λ![]()
0, że:
![]()
warunek równoległości
Definicja:
Przyjmujemy oznaczenie a![]()
a=a2. Liczbę a2 nazywamy kwadratem skalarnym wektora. Ponadto a2=|a|2.
Dowód:
a![]()
a=|a|∙|a|∙cos
(a,a)
a2=|a|2
Przykład: Obliczyć długość wektora p=4a+2b wiedząc, że |a|=3, |b|=2 oraz
(a, b)=![]()
.
|p|2=p2=p![]()
p=(4a+2b)![]()
(4a+2b)=4a![]()
4a+4a![]()
2b+2b![]()
4a+2b![]()
2b=16a![]()
a+8a![]()
b+8b![]()
a+4b![]()
b=
=16|a|2+16a![]()
b+4|b|2=16∙32+16∙3∙2∙cos![]()
+4∙22=16∙9+16∙3+16=13∙16=![]()
.
ORIENTACJA UKŁADU WSPÓŁRZĘDNYCH
Definicja orientacji układu OXY
Mówimy, że układ ortokartezjański OXY ma orientację dodatnią (orientację w prawo), jeśli przy obrocie przeciwnym do ruchu wskazówek zegara następuje pokrycie osi OY z osią OX, natomiast orientację ujemną (orientację w lewo), jeśli pokrycie to następuje przy obrocie zgodnym z ruchem wskazówek zegara.
Y X
X Y
Definicja orientacji układu OXYZ
Mówimy, że układ ortokartezjański OXYZ jest zorientowany dodatnio (ma orientację w prawo), jeśli dla patrzącego kierunku osi OZ układ OXY jest zorientowany dodatnio, a ujemnie (ma orientację ujemną), jeśli patrzący z osi OZ widzi układ OXY zorientowany ujemnie.
Z Z
Y X
X Y
Definicja:
Układ o orientacji dodatniej nazywamy układem prawym, natomiast układ o orientacji ujemnej nazywamy układem lewym.
Definicja przestrzeni zorientowanej:
Przestrzeń mającą orientację nazywamy przestrzenią zorientowaną.
Definicja:
Mówimy, że trójka wektorów a, b i c (niekoplanarnych) zaczepionych w jednym punkcie jest zorientowana zgodnie z orientacją przestrzeni (układu ortokartezjańskiego), jeżeli patrząc z końca wektora c obrót wektora a do porycia z wektorem b następuje w tym samym kierunku jak obrót osi OX do pokrycia z osią OY.
Z Z
c
c
b
b
a
a Y c X
c
X Y a
a
b
b
FAKT:
Niech a=[ax,ay,az], b=[bx,by,bz] i c=[cx,cy,cz] będą wektorami w przestrzeni. Wektory te tworzą układ w orientacji zgodnej z orientacją układu współrzędnych, jeśli:
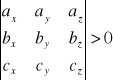
W przypadku, kiedy podany wyznacznik jest ujemny, mówimy, że orientacja układu wektorów a, b i c jest przeciwna do orientacji układu współrzędnych.
ILOCZYN WEKTOROWY WEKTORÓW
Definicja iloczyny wektorowego:
Iloczynem wektorowym pary niezerowych i nierównoległych wektorów a i b nazywamy wektor, ozn. axb, o następujących właściwościach:
długość wektora axb, ozn. |axb|, jest równa iloczynowi długości wektorów a i b oraz sinusa kąta między tymi wektorami, tj.:
|axb|=|a|∙|b|∙sin
(a,b)
wektor axb jest prostopadły do wektorów a i b, tj. axb_|_a i axb_|_b, skierowany w ten sposób, że orientacja trójki wektorów a, b i axb jest zgodna z orientacją w przestrzeni, w której się znajdują.
Jeżeli wektory a i b są równoległe lub przynajmniej jeden z nich jest wektorem zerowym to ich iloczyn wektorowy określany jest jako wektor zerowy.
Z
axb
. b
Y
a
X
WŁASNOŚCI ILOCZYNU WEKTOROWEGO:
axb=-(bxa) (antyprzemienność)
ax(b+c)=axb+axc (rozdzielność względem dodawania)
(αa)xb=ax(αb)=α(axb), α
R
Jeśli a
0 i b
0, to axb=0 wtedy i tylko wtedy, gdy a || b.FAKT:
W układzie ortokartezjańskim OXYZ iloczyn wektorowy wektorów a=[ax,ay,az] i b=[bx,by,bz] wyraża się wzorem:
axb=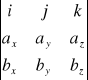
lub:
axb=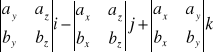
axb=[aybz-azby, azbx-axbz, bxby-aybx]
Przykład: Dane są wektory a=i+2j i b=3k-5j. Obliczyć axb i bxa.
a=[1,2,0]
b=[0,-5,3]
axb=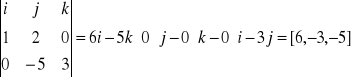
bxa =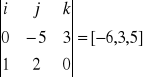
FAKT: Pole równoległoboku:
Pole równoległoboku zbudowanego na wektorach a i b jest równe długości ich iloczynu wektorowego, tj.:
Prównoległoboku =|axb|
FAKT: Pole trójkąta:
Pole trójkąta zbudowanego na wektorach a i b jest równe połowie długości ich iloczynu wektorowego, tj.:
PΔ=![]()
|axb|
Przykład: Obliczyć pole trójkąta o wierzchołkach w punktach A(1,2,1), B(2,1,-1) i C(0,1,2).
C
AB=[1,-1,-2]
PΔABC AC=[-1,-1,1]
A
B
ABxAC=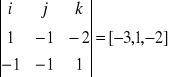
PΔABC=![]()
|ABxAC|
PΔABC=![]()
Definicja iloczynu mieszanego:
Iloczynem mieszanym uporządkowanej trójki wektorów a, b i c, ozn. symbolem abc, nazywamy liczbę równą iloczynowi skalarnemu wektora a przez wektor równy iloczynowi wektorowemu bxc, tj.:
a![]()
(bxc)
FAKT:
W ustalonym układzie ortokartezjańskim OXYZ iloczyn mieszany wektorów a=[ax,ay,az], b=[bx,by,bz] i c=[cx,cy,cz] wyraża się wzorem:
a![]()
(bxc)= 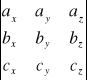
Własności iloczynu mieszanego:
a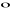
(bxc)=b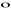
(cxa)=c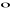
(axb) (przemienność cykliczna)
a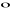
(bxc)=-c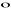
(bxa)
Twierdzenie:
Trzy wektory niezerowe a, b i c są koplanarne wtedy i tylko wtedy, gdy ich iloczyn mieszany jest równy zero, tj.: a![]()
(bxc)=0, co zapisujemy za pomocą warunku:
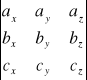
=0
FAKT: Objętość równoległościanu:
Objętość równoległościanu rozpiętego na trzech wektorach a, b i c jest równa wartości bezwzględnej z iloczynu mieszanego tych wektorów, tj.:
Vrównol.=|abc|
c
a
b
FAKT: Objętość czworościanu:
Objętość czworościanu rozpiętego na wektorach a, b i c jest równa jednej szóstej wartości bezwzględnej z iloczynu tych wektorów, tj.:
Vczwor.= ![]()
|abc|
c
a
b
Przykład: Obliczyć objętość czworościanu o wierzchołkach A(1,2,1), B(0,2,-2), C(2,1,0) i O(0,0,0).
C
OA=[1,2,1]
B OB=[0,2,-2]
OC=[2,1,0]
O
A
OA![]()
(OBxOC)=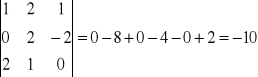
Vczwor.=![]()
PŁASZCZYZNA W PRZESTRZENI
Niech dana będzie płaszczyzna π w układzie ortokartezjańskim OXYZ. Niech punkt P0(x0,y0,z0) będzie dowolnym punktem płaszczyzny π oraz wektor N=[A,B,C] będzie do niej prostopadły.
Z
N=[A,B,C]
P0(x0,y0,z0)
π Y
X
Definicja wektora normalnego:
Wektor prostopadły do płaszczyzny nazywamy wektorem normalnym tej płaszczyzny.
Z
N=[A,B,C]
P0(x0,y0,z0)
π P(x,y,z) Y
X
P0P![]()
N=0 , P0P(x-x0, y-y0, z-z0)
A(x-x0)+B(y-y0)+C(z-z0)=0
Ax-Ax0+By-By0+Cz-Cz0=0
Ax+By+Cz+(-Ax0-By0-Cz0)=0
D
FAKT: Równanie normalne i ogólne płaszczyzny:
Równanie płaszczyzny π przechodzącej przez punkt P0(x0,y0,z0) i prostopadłej do wektora N=[A,B,C] ma postać:
π: A(x-x0)+B(y-y0)+C(z-z0)=0
Równanie to nazywamy równaniem normalnym płaszczyzny.
Wprowadzając oznaczenie D=-Ax0-By0-Cz0 otrzymujemy równanie płaszczyzny w postaci:
π: Ax+By+Cz+D=0
nazywane równaniem ogólnym płaszczyzny.
Przykład: Wyznaczyć równanie płaszczyzny π przechodzące przez punkt P0(2,1,-3) i równoległej do płaszczyzny π1:2x-3y+z-2=0.
N
P0
π π1 || π ![]()
N=N1 , N1=[2.-3,1] - z równania płaszczyzny
N=[2-3,1]
N1 π: 2(x-2)-3(y-1)+1(z+3)=0
π1 2x-3y+z-4+3+3=0
π: 2x-3y+z+2=0
FAKT:
Każde równanie postaci Ax+By+Cz+D=0, gdzie A, B i C są jednocześnie równe zeru, tzn. A2+B2+C2>0, przedstawia płaszczyznę. Płaszczyzna ta przecina oś OZ w punkcie z=![]()
, o ile C![]()
0.
Zał. A, B, C, D![]()
0
Ax+By+Cz+D=0
Ax+By+Cz=-D/:(-D)
![]()
ozn.: ![]()
FAKT: Równanie odcinkowe płaszczyzny:
Równanie płaszczyzny π odcinającej na osiach OX, OY i OZ układu współrzędnych odpowiednio odcinki a, b, c![]()
0 ma postać:
![]()
Powyższe równanie nazywamy równaniem odcinkowym płaszczyzny.
Z
(0,0,c)
(0,b,0) Y
(a,0,0)
X
Weźmy trzy punkty P1(x1,y1,z1), P2(x2,y2,z2), P3(x3,y3,z3) leżące na jednej płaszczyźnie,
tj. P1, P2, P3![]()
π
P1 P2 P1P=[x-x1,y-y1,z-z1]
P1P2=[x2-x1,y2-y1,z2-z1]
π P(x,y,z) P3 P1P3=[x3-x1,y3-y1,z3-z1]
Z warunku koplanarności wektorów: P1P![]()
(P1P2xP1P3)=0 wynika:
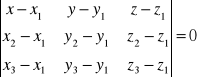
FAKT:
Równanie płaszczyzny π przechodzącej przez trzy punkty niewspółliniowe Pi(xi,yi,zi), gdzie 1<i<3 przyjmuje postać:
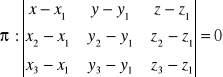
lub:
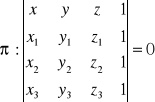
Przykład: Wyznaczyć równanie płaszczyzny π przechodzącej przez punkty A(1,2,0), B(0,2,-1) i C(1,1,1).
N
AB=[-1,0,-1]
AC=[0,-1,1] B C
.
π A
N=ABxAC![]()
ABxAC=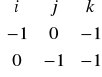
=[-1,1,1]
N=[-1,1,1] , A(1,2,0)
π: -1(x-1)+1(y-2)+1(z-0)=0
π: -x+y+z-1=0
PROSTA W PRZESTRZENI
Niech dana będzie prosta l w układzie ortokartezjańskim OXYZ przechodząca przez punkt P0(x0,y0,z0) i równoległa do danego wektora niezerowego n=[a,b,c].
Definicja wektora kierunkowego prostej:
Wektor równoległy do prostej nazywamy wektorem kierunkowym prostej.
Z
n=[a,b]c P0P=[x-x0,y-y0,z-z0]
P0(x0,y0,z0) P0P||n![]()
P(x,y,z)
Y
X
FAKT: Równanie parametryczne prostej:
Równanie prostej l przechodzącej przez punkt P0(x0,y0,z0) i równoległej do wektora n=[a,b,c] przyjmuje postać:
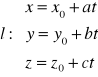
, gdzie t![]()
R
nazywaną równaniem parametrycznym prostej.
FAKT: Równanie kanoniczne prostej:
Równanie prostej l przechodzącej przez punkt P0(x0,y0,z0) i równoległej do wektora n=[a,b,c] postaci:
![]()
nazywamy postacią kanoniczną równania prostej.
Przykład: Wyznaczyć równanie prostej l przechodzącej przez punkt P0(2,1,-1) i prostopadłej do płaszczyzny π: 2x-y+z-5=0.
l
n P0 l_|_π ![]()
n || N
n=N , N=[2,-1,1]
N n=[2,-1,1] , P0[2,1,-1]
π
Weźmy dwa dowolne punkty P1(x1,y1,z1) i P2(x2,y2,z2) leżące na prostej l, tj. P1, P2![]()
l.
P1P2 || P1P
P2(x2,y2,z2) P1P2=[x2-x1,y2-y1,z2-z1]
P1P=[x-x1,y-y1,z-z1]
P1(x1,y1,z1)
P(x,y,z)
FAKT:
Równanie prostej l przechodzącej przez dwa punkty Pi(xi,yi,zi), gdzie 1<i<2, w postaci parametrycznej przedstawia się zależnością:
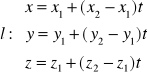
, gdzie t![]()
R,
natomiast w postaci kanonicznej równaniem:
![]()
Przykład: Wyznaczyć równanie prostej l przechodzącej przez punkty P1(1,2,3) i P2(3,1,-1).
n=P1P2
n P2 n=[2,-1,-4]
P1 P1(1,2,3)
FAKT: Równanie krawędziowe prostej:
Prostą l, która jest częścią wspólną dwóch nierównoległych płaszczyzn π1: A1x+B1y+C1z+D1=0 i π2: A2x+B2y+C2z+D2=0 zapisujemy w postaci:
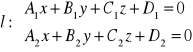
nazywanej równaniem krawędziowym prostej.
N1
N2
n
π2
l π1
Przykład: Przedstawić prostą 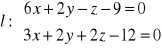
w postaci kanonicznej i parametrycznej.
N1=[6,2,-1]
N2=[3,2,2]
N=N1xN2=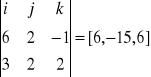
P0=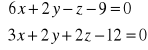
x=0
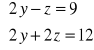
3x=-3
z=1
2y=10![]()
y=5
równanie parametryczne: 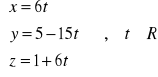
równanie kanoniczne: ![]()
PĘK PŁASZCZYZN
Definicja pęku płaszczyzn:
Pękiem płaszczyzn nazywamy zbiór wszystkich płaszczyzn przecinających się wzdłuż jednej prostej.
Weźmy dwie płaszczyzny π1 i π2:
π1: A1x+B1y+C1z+D1=0
π2: A2x+B2y+C2z+D2=0
Jeżeli wektory normalne tych płaszczyzn nie są kolinearne, to płaszczyzny te przecinają się wzdłuż pewnej prostej l i wyznaczają pewien pęk płaszczyzn.
Twierdzenie:
Płaszczyzna π należy do pęku płaszczyzn wyznaczonego przez dwie przecinające się płaszczyzny π1 i π2 wtedy i tylko wtedy, gdy istnieją liczby rzeczywiste λ1 i λ2, nierówne jednocześnie zero, tj.: λ12+λ22>0, takie, że równanie taj płaszczyzny przedstawia się w postaci:
λ1(A1x+B1y+C1z+D1)+λ2(A2x+B2y+C2z+D2)=0
Powyższe równanie nazywamy równaniem pęku płaszczyzn.
Przykład: Wyznaczyć równanie płaszczyzny π przechodzącej przez krawędź przecięcia płaszczyzn
π1:-x+2y+z-1=0 i π2: 2x-y+z=0 oraz punkt P0(1,2,-1).
Równanie pęku płaszczyzn wyznaczonych przez π1 i π2:
λ1(-x+2y+z-1)+λ2(2x-y+z)=0
λ1(-1+4-1-1)+λ2(2-2+2)=0
λ1+2λ2=0
niech λ2=1![]()
λ1=-2
-2(-x+2y+z-1)+1(2x-y+z)=0
π: 4x-5y-2z+4=0
WZAJEMNE POŁOŻENIE PUNKTÓW, PROSTYCH I PŁASZCZYZN
Definicja rzutu punktu na płaszczyznę i na prostą:
Rzutem prostokątnym punktu P na płaszczyznę π nazywamy punkt P' tej płaszczyzny spełniający warunek:
PP' _|_ π
Analogicznie rzutem prostokątnym punktu P na prostą l nazywamy punkt P' tej prostej spełniający warunek:
PP' _|_ l
Przykład: Znaleźć rzut prostokątny punktu P(3,-2,1) na płaszczyznę π: 2x-y+3z=0
N
P
1º l_|_π ![]()
P![]()
l
n=N![]()
n=[2,-1,3]
P' P(3,-2,1)
π
2º P':![]()
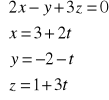
2(3+2t)-(2-t)+3(1+3t)=0
6+4t+2+t+3+9t=0
14t=-11
t=![]()
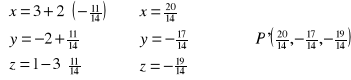
Przykład: Znaleźć rzut prostokątny punktu P(2,-1,4) na prostą ![]()
n
P
P' 1º l_|_ π ![]()
P![]()
π ![]()
N=n , N=[1,-1,-3]
π: 1(x-2)-1(y+1)-3(z-4)=0
π π: x-y-3z+9=0
l
2º P': ![]()
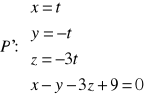
t+t+9t+9=0
11t=-9
t=![]()
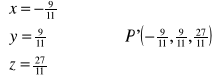
UWAGA: Odległość punktu P od płaszczyzny π jest równa długości odcinka PP', gdzie P' jest rzutem prostokątnym punktu P na płaszczyznę π. Analogicznie, odległość punktu P od prostej l jest równa długości odcinka PP', gdzie P' jest rzutem prostokątnym punktu P na prostą l.
FAKT: Odległość punktu od płaszczyzny:
Odległość punktu P0(x0,y0z0) od płaszczyzny π: Ax+By+Cz+D=0, wyraża się wzorem:
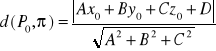
FAKT: Odległość płaszczyzn równoległych:
Odległość między płaszczyznami równoległymi π1 i π2 o równaniach π1: A1x+B1y+C1z+D1=0 i
π2: A2x+B2y+C2z+D2=0 wyraża się wzorem:
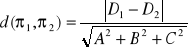
FAKT: Wzajemne położenie płaszczyzn:
Niech dane będą dwie płaszczyzny o równaniach:
π1: A1x+B1y+C1z+D1=0
π2: A2x+B2y+C2z+D2=0
Mówimy, że:
płaszczyzny π1 i π2 są równoległe, tj.: π1 || π2, wtedy i tylko wtedy, gdy:
![]()
płaszczyzny π1 i π2 pokrywają się wtedy i tylko wtedy, gdy:
![]()
płaszczyzny π1 i π2 są prostopadłe, tj.: π1 _|_ π2, wtedy i tylko wtedy, gdy:
A1A2+B1B2+C1C2=0
płaszczyzny π1 i π2 przecinają się pod dowolnym kątem różnym od
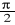
, jeśli nie zachodzi żaden z wyżej wymienionych przypadków. Wówczas układ:
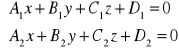
podaje równanie prostej będącej krawędzią przecięcia tych płaszczyzn.
α - kąt, pod jakim przecinają się płaszczyzny π1 i π2
![]()
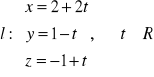
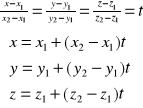
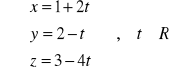
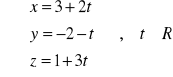
Wyszukiwarka