Geometria analityczna w przestrzeni, Matematyka

Pobierz cały dokument geometria.analityczna.w.przestrzeni.doc Rozmiar 455 KB

Fragment dokumentu:

GEOMETRIA ANALITYCZNA W PRZESTRZENI

• ALGEBRA WEKTORÓW

• Definicja kartezjańskiego układu współrzędnych:

Kartezjańskim układem współrzędnych prostokątnych (układem ortogonalnym lub ortokartezjańskim) nazywamy uporządkowaną trójkę półosi regularnych wzajemnie do siebie prostopadłych o wspólnym początku i wspólnej jednej długości. Stosujemy oznaczenie OXYZ.

• Definicja:

Położenie dowolnego punktu P w przestrzeni można określić za pomocą trójki liczb nazywanych współrzędnymi punktu P, co zapisujemy: P(x_p,y_p,z_p), gdzie:

x_p - oznacza współrzędną prostokątną rzutu punktu P na oś OX

y_p - oznacza współrzędną prostokątną rzutu punktu P na oś OY

z_p - oznacza współrzędną prostokątną rzutu punktu P na oś OZ

Z

z_p

P(x_p,y_p,z_p)

y_p Y

x_p

X

• FAKT:

Weźmy punkty A(x₁,y₁,z₁) i B(x₂,y₂,z₂). Punkty te wyznaczają w układzie OXYZ odcinek
, którego długość wyraża się wzorem:

• Definicja wektora:

Parę uporządkowaną punktów A i B w przestrzeni nazywamy wektorem i oznaczamy symbolem AB lub a, zapisujemy AB=(a_x,a_y,a_z), gdzie a_x,a_y,a_z nazywamy współrzędnymi wektora AB w układzie OXYZ i obliczamy z zależności:

a_x=x₂-x₁, a_y=y₂-y₁, a_z=z₂-z­₁

• FAKT:

Długość wektora AB, oznaczamy: |AB| lub |a| wyraża się wzorem:

Przykład: Obliczyć długość wektora rozpiętego między punktami P₁(0,2,-1) i P₂(3,0,1).

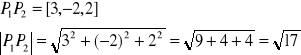
• Definicja sumy wektorów:

Sumą wektorów a=[a_x,a_y,a_z] i b=[b_x,b_y,b_z] nazywamy wektor, którego współrzędne tworzymy dodając odpowiednie składowe wektorów a i b, tj. wektor postaci:

a + b = [a_x+b_x ; a_y+b_y­ ; a_z+b_z]

a

a + b

b

b

• Własności sumy wektorów:

1. 
   
   
   
   a+b=b+a (przemienność)

2. 
   
   
   
   
   
   (a+b)+c=a+(b+c) (łączność)

3. 
   
   
   
   
   a+0=0+a=a (element neutralny dodawania wektorów)

4. 
   
   
   a+(-a)=0 (wektor przeciwny)

• Definicja iloczynu wektora przez liczbę:

Iloczynem wektora (niezerowego) a przez liczbę λ
R, λ
0 nazywamy wektor λa skierowany zgodnie ze skierowaniem wektora a jeśli λ>0, a przeciwnie, jeśli λ<0, o długości równej |λa| w postaci. λa=[ λa_x, λa_y, λa_z].

Jeśli λ=0 lub a=0 to iloczyn ten jest wektorem zerowym.

• Własności iloczynu wektora przez liczbę:

1. 
   
   
   (λ+α)a=λa+αa

2. 
   
   λ(αa)=(λα)a

dla α, λ
R

• Definicja kombinacji liniowej n wektorów:

  
  

  Pobierz cały dokument geometria.analityczna.w.przestrzeni.doc rozmiar 455 KB