Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej |
||||||||
Nazwisko i imię Ignatowicz Paweł studenta: |
Symbol grupy MD 103.1c |
|||||||
Data wykonania ćwiczenia:
|
Symbol ćwiczenia: O.12.3 |
Temat zadania: Wyznaczanie charakterystyki prądowo-strumieniowej fotoogniwa. |
||||||
Zaliczenie: |
Ocena: |
Data:25,11,99 |
Podpis |
|||||
Tabela pomiarów.
S = ... r = 0,15 m |
||||
U [V] |
I [A] |
P [W] |
|
I |
7,4 |
1,225 |
9,065 |
1,789 |
8,4 |
7,2 |
1,225 |
8,82 |
1,741 |
7,8 |
7,0 |
1,20 |
8,4 |
1,658 |
7,2 |
6,8 |
1,175 |
7,99 |
1,577 |
6,4 |
6,6 |
1,15 |
7,59 |
1,498 |
5,6 |
6,4 |
1,15 |
7,36 |
1,453 |
4,7 |
6,2 |
1,125 |
6,975 |
1,378 |
4,0 |
6,0 |
1,10 |
6,6 |
1,303 |
3,4 |
5,8 |
1,025 |
5,945 |
1,173 |
2,8 |
5,6 |
1,05 |
5,88 |
1,161 |
2,3 |
5,4 |
1,05 |
5,67 |
1,119 |
1,8 |
5,2 |
1,00 |
5,2 |
1,026 |
1,4 |
5,0 |
1,00 |
5,0 |
0,869 |
1,0 |
Obliczenia.
P= U ![]()
I P-moc [P]=W
P![]()
= 7,4V ![]()
1,225A = 9,065W U-napięcie [U]=V
I-natężenie [I]=A
![]()
[![]()
]=lumen
![]()
-strumień świetlny padający na fotokomórkę
k=0,00155 wat/lumen dla światła o długości fali ![]()
555 nm [r]=m
r- odległość fotokomórki od żródła światła r=15cm=0,15m
![]()
=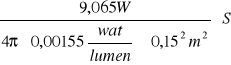
=![]()
20684,44639![]()
![]()
= 1,789 lm
Krótka teoria.
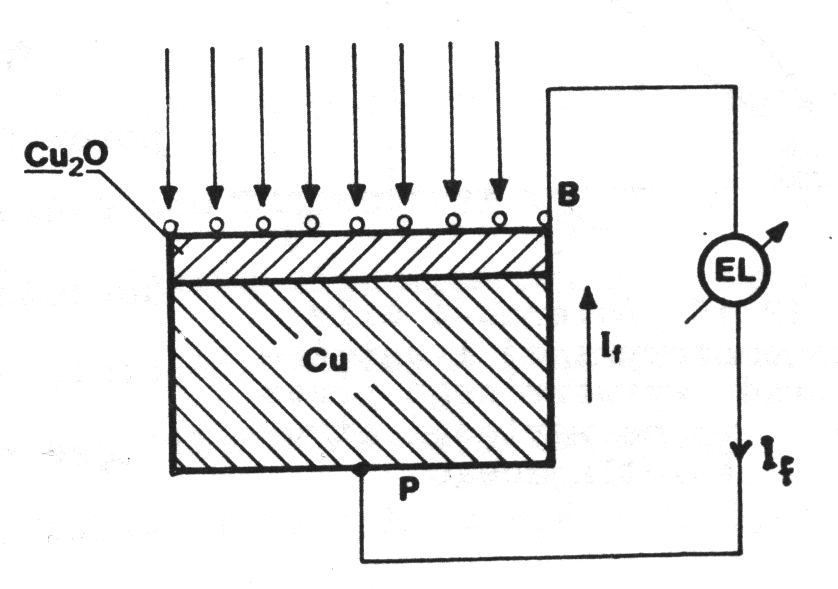
Zasada budowy i działania fotoogniwa.
Jak było wcześniej powiedziane, w ogniwie fotoelektrycznym mamy do czynienia z tzw. zjawiskiem fotowoltaicznym, które
powstaje na granicy pomiędzy metalem a półprzewodnikiem pod wpływem promieni świetlnych. Dla przykładu omówimy tutaj budowę fotoogniwa miedziowego, którego schemat przedstawia powyższy rysunek Składa się
ono z płytki wykonanej z czystej miedzi pokrytej (przez utlenianie)
przeźroczystą dla światła cienką
półprzewodzącą warstwą tlenku miedziowego. Od góry jako druga elektroda nałożona jest siatka z miedzi lub innego metalu. Jeśli połączymy siatkę B z płytką P przez elektrometr EL to wskaże on przepływ prądu o natężeniu If. Na granicy Cu - Cu20 powstaje warstwa zaporowa, która ma właściwości przepuszczania elektronów w kierunku: od tlenku miedziowego do miedzi. Wyzwolone pod wpływem światła z Cu20 elektrony przebywają warstwę zaporową i przechodzą do płytki miedzianej ładując ją ujemnie jednocześnie tlenek miedziowy i elektroda zewnętrzna (siatka) ładują się dodatnio. Tym samym w czasie oświetlania fotoogniwa powstaje na jego elektrodach różnica potencjałów, która jest podtrzymywana kosztem energii padających kwantów światła.
Zjawisko fotoelektryczne wewnętrzne. Fotoelementy pólprzewodnikowe.
przenikliwe promieniowanie świetlne może wyzwalać w kryształach wolne elektrony i dziury. to znaczy nośniki prądu. Zjawisko to nazywamy efektem fotoelektrycznym wewnętrzym w odróżnieniu od zjawiska fotoelektrycznego zewnętrznego, które zachodzi na powierzchni ciał. Uwolnione fotoelektrony, znajdując się w polu elektrycznym, przyczyniają się do powstawania fotoprzewodnictwa. Powstawanie swobodnych elektronów albo dodatnich dziur pod wpływem absorbowanego promieniowania zachodzi we wszystkich krysztalach będących izolatorami czy półprzewodnikami. W diamencie, który jest dobrym izolatorem, zjawisko fotoelektryczne zachodzi przy naświetlaniu kryształu promieniowaniem ultrafioletowym. W' kryształach krzemu i germanu oraz w selenie wywołuje je światło widzialne; niektóre związki, jak np. PbS uzyskuja przewodnictwo już pod wpływem podczerwieni.
Na zasadzie efektu fotoeIektrycznego wewnętrznego w pólprzewodnikach działają fotokomórki, tzw. zaporowe oraz fotoogniwa. Działanie fotokomórki zaporowej... W ciemności opór płytki półprzewodnikowej jeśt tak duży, że praktycznie prąd w obwodzie nie płynie. Oświetlenie płytki wytwarza w niej nośniki prądu, to jest swobodne elektrony i dziury; opór płytki, znacznie spada tak, że przyłożone do końców płytki napięcie elektryczne powoduje przepływ prapdu w obwodzie.
Fotoogniwo jest to urządzenie
przetwarzające energię świetlną na elektryczną. rys 70.1 przedstawia schematycznie przekrój fotoogniwa, tzw. miedziowego. Podstawowym materiałem jest tu tlenek miedzi Cu2O. Jest to półprzewodnik typu P, wykazujący przewodnictwo dziurowe. Nośnikami prądu są w nim zatem dziury, swobodnych elektronów natomiast prawie nie ma. Na płytkę miedzianą jest naniesiona warstwa
Cu20, na którą jest napylona cienka warstwa metaiu np.: platyny, złota, srebra czy miedzi. Przypuśćmy, że warstwy, z których składa się fotoogniwo nie stykają się ze sobą. Wówczas każda z nich jest elektrycznie obojętna. W płytce z miedzi elektrony swobodne są rozłożone ze stałą gęstością, w warstwie Cu20 tak samo równomiernie są rozłożone dziury, a w warstewce Cu - swobodne elektrony {rys. '. ~.2). Jeżeli warstwy te zetkniemy ściśle ze soba, jak
to ma miejsce w przypadku fotoogniwa; to wskutek ruchu ładunków część elektronów z warstewki Cu przedyfunduje do Cu2O i na odwrót , pewna ilość dziur z Cu20 do warstewki Cu.
Wskutek tego na granicy obu warstw w warstewce Cu
gromadzi się ładunek dodatni, w warstwie Cu2O zaś ładunek ujemny. Te ładunki powierzchniowe wstrzymują dalszą dyfuzję dziur z warstwy Cu20 i elektronów z warstewki Cu.Podobna sytuacja będzie zachódżić na granicy warstwy Cu20 i plytki Cu. Powyższą sytuację przedstayia rys.
. : 3. W dolnej części te
go rysunku pokazano rozkład potenejału elektrycznego w trzech omawianych powyżej obsza
rach. Wskutek dyfuzji
elektronów z warstwy miedzi do warstwy Cu20 ' oraz dziur w kierunku odwrotnym, warstwy miedzi mają potenejał dodatni względem warstwy Cn20.
Jeżeli przez cienka warstewkę Cu pada na ogniwo promieniowanie 0 odpowiedniej długości fali, w pólprzewodniku Cu2O na granicy z warstewką Cu po
wstają dziury i swobodne elektrony, co narusza dotychczasową równowagę dyfuzyjną. Flektrony pod wpływem granicznego skoku potencjału przechodżą z warstwy Cu20 do warstewki Cu i po przewodniku zamykającym obwód dostają się do płyty Cu. Zwiększenie ilości elektronów w płytce Cu obniża jej potencjał, co powoduje zmniejszenie skoku potenejału na granicy warstwy Cu20 i płyty Cu. Umożliwia to przechodzenie elektronów z płyty Cu do warstwy Cu2O (rys. .4). W ten sposób zamyka się obwód prądu. W warstwie Cu2O elektrony rekombinują z dziurami, ale działające .wciąż promieniowanie wytwarza nowe pary dziura-elektron, co powoduje stały przepływ prądu elektrycznego. W ten sposób energia promieniowania zamienia się bezpośrednio na energię prądu elektrycznego.
Fotoogniwa znalazły szerokie zastosowanie w światłomierzach fotograficznych. Baterie fotoogniw stanowią również często źródło zasilania mechanizmów uruchamiających aparaturę w sztucznych satelitach i pojazdach kosmicznych.
4.Schemat ćwiczenia i opis wykonania.
Układ pomiarowy zestawiamy wg. Schematu:
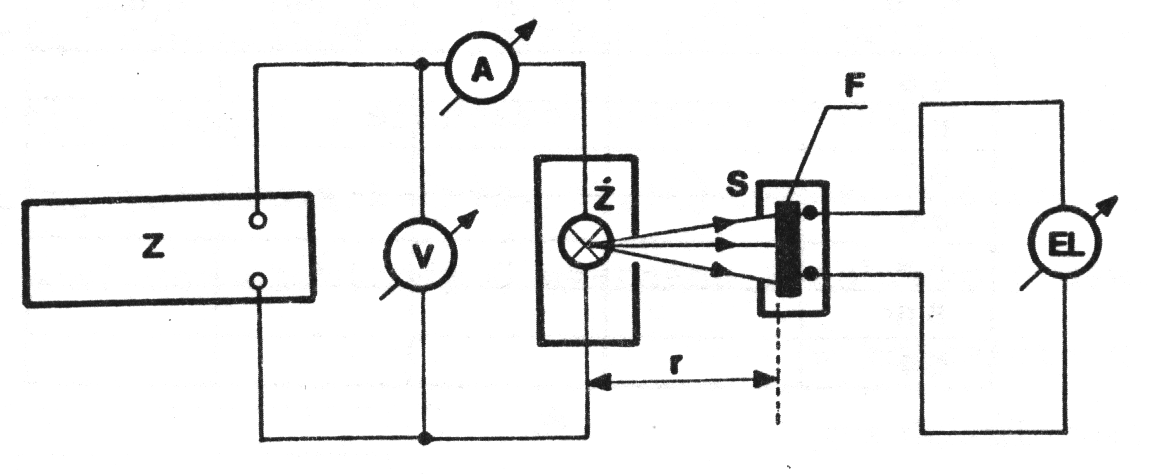
Zestaw doświadczalny do pomiaru czułości fotoogniw.
z![]()
- zasilacz stabilizowany prądu stałego,
V-woltomierz 0 - 10 V,
A-amperomierz 0 - 5 A,
Ż- żarówka 6V / 20W,
F-fotoogniwo w osłonie (o powierzchni okienka S),
EL- elektrometr,
r- odległość między żarówką a fotoogniwem.
Źródło światła i fotoogniwo umieszczamy na ławie optycznej w odległości
r![]()
0,25m. Zakres elektrometru dobieramy tak, aby można było mierzyć maksymalne natężenie prądu dawanego przez fotoogniwo. Napięcie zasilania żarówki zmieniamy przy pomocy pokrętła zasilacza Z granicach od 6,6 V do 5,4 V co 0,2 V, mierząc za każdym razem natężenie prądu płynącego przez żarówkę (amperomierz A) oraz natężenie prądu dawanego przez fotoogniwo (elektrometr EL). Stosowanie szerszych przedziałów zmian napięcia na żarówce oświetlającej nie jest wskazane ze względu na to, że zbytnio zmieni się skład widmowy emitowanego przez nią promieniowania.
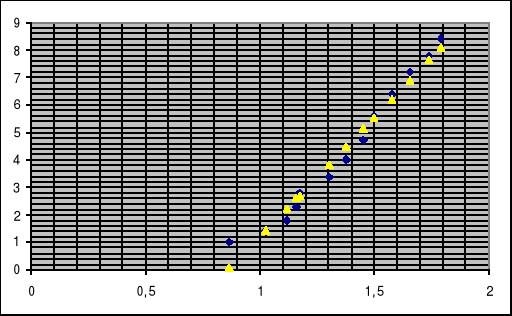
5.Opracowanie wyników pomiarów.
a) błędy przypadkowe
lp |
x |
y |
x |
x |
w |
a |
b |
y |
|
( |
|
1 |
1,789 |
8,4 |
3,200 |
15,028 |
1 |
|
|
8,053 |
-0,347 |
0,120 |
|
2 |
1,741 |
7,8 |
3,031 |
13,580 |
1 |
|
|
7,636 |
-0,164 |
0,027 |
|
3 |
1,658 |
7,2 |
2,749 |
11,938 |
1 |
|
|
6,915 |
-0,285 |
0,081 |
|
4 |
1,577 |
6,4 |
2,487 |
10,093 |
1 |
|
|
6,211 |
-0,189 |
0,037 |
|
5 |
1,498 |
5,6 |
2,244 |
8,389 |
1 |
|
|
5,525 |
-0,075 |
0,006 |
|
6 |
1,453 |
4,7 |
2,111 |
6,815 |
1 |
|
|
5,134 |
0,434 |
0,188 |
|
7 |
1,378 |
4,0 |
1,899 |
5,512 |
1 |
8,690 |
-7,493 |
4,482 |
0,482 |
0,232 |
|
8 |
1,303 |
3,4 |
1,698 |
4,430 |
1 |
|
|
3,830 |
0,43 |
0,185 |
|
9 |
1,173 |
2,8 |
1,376 |
3,284 |
1 |
|
|
2,700 |
-0,1 |
0,01 |
|
10 |
1,161 |
2,3 |
1,348 |
2,670 |
1 |
|
|
2,596 |
0,296 |
0,088 |
|
11 |
1,119 |
1,8 |
1,252 |
2,014 |
1 |
|
|
2,231 |
0,431 |
0,186 |
|
12 |
1,026 |
1,4 |
1,053 |
1,436 |
1 |
|
|
1,423 |
0,023 |
0,0005 |
|
13 |
0,869 |
1,0 |
0,755 |
0,869 |
1 |
|
|
0,059 |
-0,941 |
0,885 |
|
=17,745 |
|
=25,203 |
=86,058 |
|
|||||||
![]()
=2,0455
D = 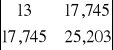
=13 25,203- 17,745 17,745= 12,754
a = 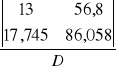
= 8,690
b = 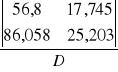
= - 7,493![]()
![]()
a = 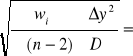
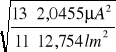
= 0,435![]()
![]()
b = 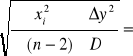
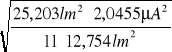
= 0,606 ![]()
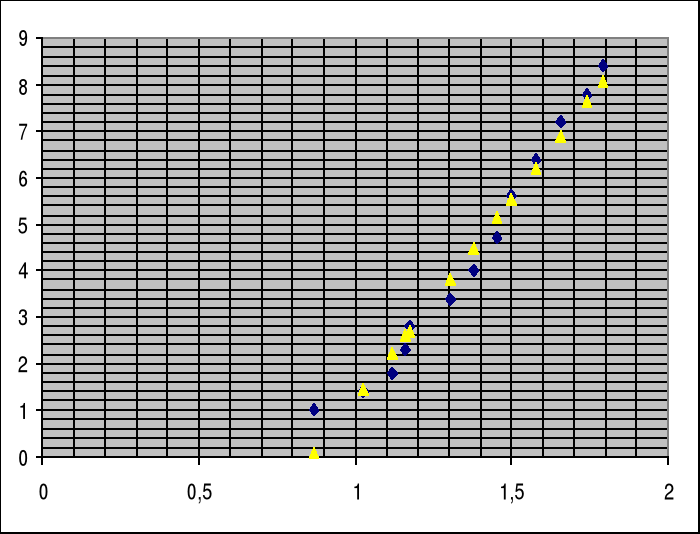
Interesujące nas równanie prostej zapiszemy w postaci.
y = (a![]()
![]()
a)x+(b![]()
b) ![]()
I![]()
= (8,690 ![]()
0,435) ![]()
![]()
![]()
+(-7,493 ![]()
0,606) ![]()
b) Błąd względny maksymalny - metoda różniczkowa.
![]()
(K) =![]()
=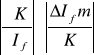
+![]()
+![]()
+![]()
![]()
![]()
![]()
![]()
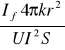
![]()
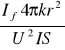
![]()
![]()
![]()
(K) =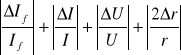
![]()
![]()
- błąd bezwzględny pomiaru napięcia wynikający z niedokładności woltomierza.
![]()
- błąd bezwzględny pomiaru napięcia prądu spowodowany niedokładnością odczytu.
![]()
![]()
- błąd bezwzględny pomiaru natężenia wynikający z niedokładności amperomierza.
![]()
- błąd bezwzględny pomiaru natężenia prądu spowodowany niedokładnością odczytu.
![]()
![]()
- błąd bezwzględny pomiaru napięcia wynikający z niedokładności woltomierza.
![]()
- błąd bezwzględny pomiaru napięcia prądu spowodowany niedokładnością odczytu.
![]()
r = 2 mm
![]()
=![]()
=![]()
= 0,0375 V ![]()
V
![]()
=![]()
=![]()
V
![]()
= ![]()
=![]()
A ![]()
![]()
= ![]()
= ![]()
![]()
=![]()
=![]()
=0,2![]()
A ![]()
= 2![]()
0,2![]()
= . =0,4![]()
A
![]()
= ![]()
=![]()
= 0,2![]()
A
![]()
(K) = ![]()
![]()
(K) = 0,01 + 0,0638 + 0,0222 + 0,0266 = 0,1226
i wyrażając w procentach :
![]()
0,1226 100% = 12,26%
błąd bezwzględny maksymalny wynosi :
![]()
K =![]()
K![]()
= 0,1226 8,690 = 1,0654
wynik pomiaru zapiszemy :
K = (K![]()
![]()
![]()
)
K = (8,690 ![]()
1,0654)
7,6246 < K< 9,7554
1
7
Wyszukiwarka