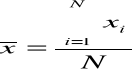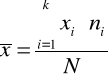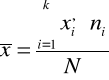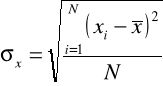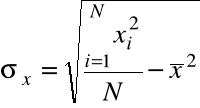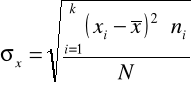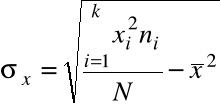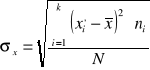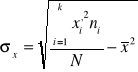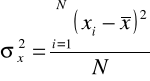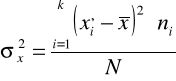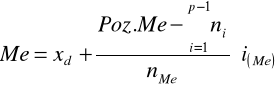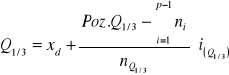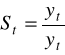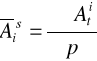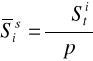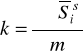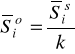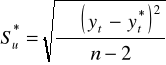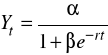Szereg wyliczający (prosty)	Szereg rozdzielczy z przedziałami jednostkowymi		Szereg Roz. z równymi przedz. klas.
Średnia arytmetr.			gdzie: k - liczba przedziałów klasowych w schemacie klasyfikacyjnym
Odchylenie standardowe	lub	lub		lub
Wariancja

Mediana - kwartyl drugi	Pozycja mediany			pozycje mediany kumulowanie liczebności ustalamy przedział p, który zawiera medianę W przypadku, gdy liczba jednostek jest parzysta i jest ich ponad 100 lub zamiast liczebności absolutnych posługujemy się odsetkiem ustalamy wartość mediany tylko dla jednostki N/2.
		Parzyste N	Nieparzyste N
	Inne kwantale -kwartale I i III	Pozycja kwartyli			pozycje kwartyli kumulowanie liczebności ustalamy przedział p, który zawiera kwartyl W przypadku, gdy liczba jednostek jest parzysta i jest ich ponad 100 lub zamiast liczebności absolutnych posługujemy się odsetkiem

Współczynnik zmienności

Współczynnik asymetrii

>0 prawostronna

<0 lewostronna

Dominanta np. w przypadku szer. Rozdz. zbud . metoda badania wariancyjnego

Gdzie: x_d -dolna granica przedziału

n_D - liczebność dominująca

n_D-1 - liczebność poprzedzająca dominującą

n_D+1 - liczebność następująca dominującą

i - rozpiętość przedziału

Mierniki koncentracji

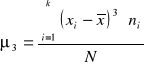
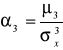
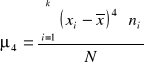
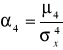
<3 brak konc.

>3 koncentracja

N	k
<50	4-5
51-100	5-7
101-200	6-8
201-500	7-10

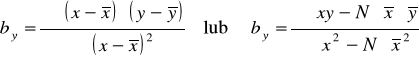
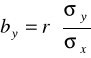
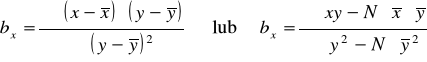
odchylenie standardowe składnika resztowego S_{u :}

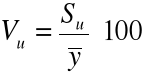
współczynnik zbieżności (indeterminacji)

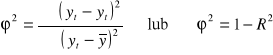
Błędy średnie szacunku ocen parametrów funkcji regresji:

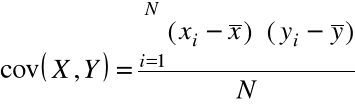
kowariancja

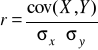
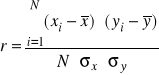
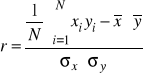
Współczynnik korelacji liniowej Pearsona

x_t - wartości zmiennej objaśniającej ( t = 1, 2, ..., N ), a_y - wyraz wolny,

b_y - współczynnik regresji Y względem X.

y_t - wartości zmiennej Y dla t = 1, 2, ..., N,

a_x - wyraz wolny,

b_x - współczynnik regresji X względem Y.

współczynnik zmienności resztowej V_u

współczynnik determinacji R² :

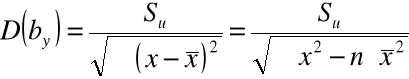
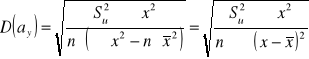
Równość Pearsona

typ.obsz.zmienn.

Obsz. Zmienności wynikający z reguły 3 sigm

Standaryzacja zmiennych

Współczynnik Czuprowa

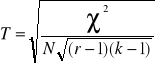
Współczynnik kontengencji

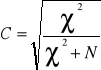
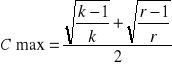
Model regresji w przypadku trzech zmiennych:

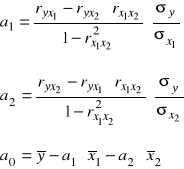
odchylenie standardowe składnika resztowego S_{u :}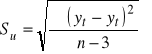

Współczynnik zmienności resztowej V_u:

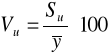
Współczynnik zgodności

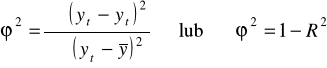
n_e -liczebności empiryczne

n_t -liczebności teoretyczne

Współczynniki korelacji cząstkowej:

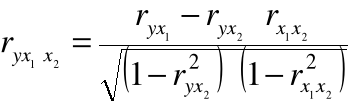
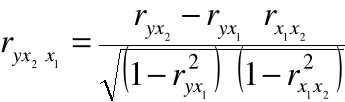
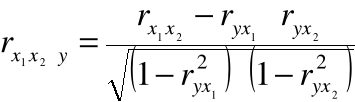
współczynnik korelacji wielu zmiennych

Indeksy indywidualne

łańcuchowy

średni indeks łańcuchowy

średnie tempo

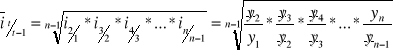
Indeksy agregatowe

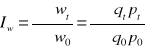
indeks wartości

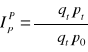
indeks cen Paschego

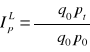
indeks cen Laspeyresa

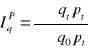
indeks ilości Paschego

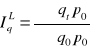
indeks ilości Laspeyresa

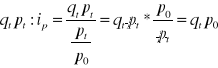
r i k - wymiary tabeli - liczba wierszy i liczba kolumn

jednopodstawowy

t=1,2,3n…,n

wsp. kor. rang Spearmana

Wahania sezonowe: Aproksymanta trendu

	Model addytywny	Model multiplikatywny
Eliminacja trendu
Surowe wskaźniki sezonowości
Elimin. Wahań przypadkowych
obliczanie oczyszczon. Wskaźnik. sezonowości
Prognozowanie zmiennej sezonowej

lub Prognoza przedziałowa zmiennej sezonowej

i - numer sezonu ( i = 1, 2, ..., m),

p - liczba lat badanych.

Przy

czym

Przy

czym

Gdy nie występuje trend:

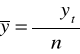
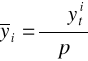
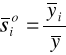
poziom badanej zmiennej w analizowanym przedziale czasowym

średnie poziomy badanej zmiennej dla jednoimiennych podokresów sezonowych

wskaźniki sezonowości dla poszczególnych sezonów

Modele szeregów czasowych

1. 1. addytywny:

2. multiplikatywny

− odchylenie standardowe składnika resztowego szeregu czasowego,

− wartości teoretyczne szeregu czasowego … przy czym

− trend

− wahanie cykliczne

− wahanie sezonowe

−wahania przypadkowe

t − zmienna czasowa

Metoda mechaniczna wyrównania szeregów czasowych:

k- stała wygładzania

skrócenie: nieparzyste k :
; parzyste k
…
-> śr. ruch

Metoda analityczna wyrównania szeregów czasowych:

funkcja liniowa	f. paraboliczna	f. potęgowa
f. wykładnicza	f. hiperboliczna	f. logistyczna

Dla

Parametry

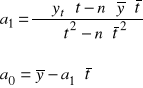
Odch.cząst.skł reszt:

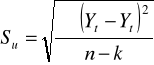
współczynnik zmienności losowej

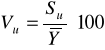
współczynnik zgodności współczynnik determinacji

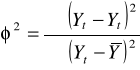
Błędy średnie: Oceny parametrów:

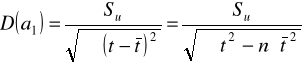
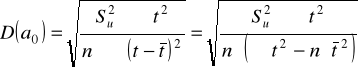
Ekstrapolacja f, trendu:
(liniowa:
)

Średni błąd prognozy ex ante względny bł. prog.ex ante

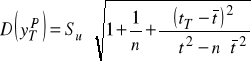
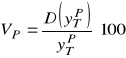
wysoce precyzyjna;
dostat.;
niedostat

t = 1, 2, 3, ..., n; f(t) − f trendu,
− składnik losowy

y_t − poziom Bad. zjaw. w jednostce czasu t,

t − zmienna czasowa (t = 1, 2, …, n),

u_t − realizacje składnika losowego,

− parametry liniowej funkcji trendu.

Sr y− śr. Aryt. zmiennej Y w przedziale czas. <1, n>,

Sr T − średnia arytmetyczna zmiennej czasowej,

− realizacje zmiennej Y w okresie t (t = 1, 2, …, n).

− wartości empiryczne zmiennej ( t = 1, 2, 3, ..., n ),

− wartości teoret. ( war trendu ) zmienn. objaśnianej,

k − liczba szacowanych parametrów trendu.

− średnia arytmetyczna zmiennej objaśnianej

- mały błąd

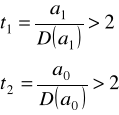
>0 prawostronn

<0 lewo.stronna

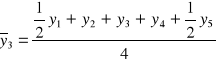
Średnia ruchoma

3-okresowa dla poziomu 2

Średnia ruchoma

4-okresowa dla poziomu 3

---