Rok: pierwszy Kierunek studiów: BUDOWNICTWO |
Imię i nazwisko:
Kamil Gaida
|
Data: 22.04.2015
|
Numer ćwiczenia:
10
|
Temat ćwiczenia:
Badanie ruchu bryły sztywnej
|
Ocena:
|
Cel ćwiczenia
Celem wykonania tego ćwiczenia jest sprawdzenie zasady zachowania energii mechanicznej, jak również wyznaczenie momentu bezwładności I bryły sztywnej.
W ćwiczeniu używa się kuli staczającej się z równi pochyłej. Ruch ten jest złożony z ruchu postępowego i obrotowego bryły sztywnej. Energia potencjalna kuli znajdującej się na wysokości h zamienia się całkowicie u podstawy równi, gdzie h=0, na energię kinetyczną ruchu postępowego i obrotowego. Wyrażone to jest równaniem wynikającym z zasady zachowania energii:
![]()
gdzie:
![]()
- masa kulki,
![]()
- przyspieszenie ziemskie,
![]()
- wysokość równi,
![]()
- prędkość końcowa kulki,
![]()
- moment bezwładności kulki,
![]()
- prędkość kątowa.
Na podstawie tej równości należy wyznaczyć moment bezwładności ![]()
kuli i porównać z wartością teoretyczną.
Część teoretyczna
Równia pochyła jest jedną z maszyn prostych. Urządzenia, których działanie oparte jest na równi były używane przez ludzkość od zarania dziejów. Przykładem równi jest dowolna pochylnia.
Maszyny proste - (w fizyce) idealizacje prostych rzeczywistych mechanizmów urządzeń mechanicznych wprowadzone w celu wyjaśnienia działania mechanizmów urządzeń ułatwiających wykonanie pewnych czynności (pracy) poprzez zmianę wartości lub kierunku działania siły wykonującej daną pracę. Maszyny proste określają wzajemną relację pomiędzy siłami poruszającymi a użytecznymi w stanie równowagi, w warunkach spoczynku, ruchu jednostajnego postępowego lub obrotowego przy zaniedbaniu sił tarcia i inercji układu.
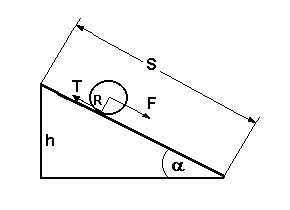
Zgodnie z zasadą zachowania energii, praca wykonana nad danym układem bez maszyny prostej oraz z użyciem dowolnego zbioru maszyn prostych jest zawsze taka sama. Korzyść polega na tym, że możemy np. użyć mniejszej siły, ale wówczas musimy pokonać dłuższą drogę.
Równia to płaska powierzchnia nachylona do poziomu pod pewnym kątem, po powierzchni równi przesuwa się ciało.
Moment bezwładności, miara bezwładności ciała w ruchu obrotowym. Charakteryzuje rozkład masy w ciele. Moment bezwładności ciała względem osi z nazywane jest wyrażenie:
![]()
Momenty bezwładności wybranych brył:
Przebieg doświadczenia
Ćwiczenie polegało na stoczeniu 3 kul, o różnych masach i średnicach, po równi pochyłej o długości 3,3m i zmierzeniu czasu ich staczania. Dla każdej kuli dokonaliśmy po 10 pomiarów przy dwóch różnych wysokościach.
Tabela pomiarowa:
h1 |
t [s] |
h2 |
t [s] |
||||
|
kula 1 m1=286,39 g |
kula 2 m2=2,63 g |
kula 3 m3=78,71 g |
|
kula 1 m1=286,39 g |
kula 2 m2=2,63 g |
kula 3 m3=78,71 g |
0,46 |
2,557 |
3,068 |
2,703 |
0,23 |
3,687 |
4,594 |
4,104 |
|
2,558 |
3,045 |
2,671 |
|
3,681 |
4,743 |
3,948 |
|
2,549 |
3,090 |
2,687 |
|
3,686 |
4,649 |
4,134 |
|
2,567 |
3,129 |
2,657 |
|
3,709 |
4,584 |
3,949 |
|
2,553 |
3,134 |
2,681 |
|
3,700 |
4,567 |
4,074 |
|
2,553 |
3,114 |
2,662 |
|
3,682 |
4,603 |
3,993 |
|
2,553 |
3,083 |
2,695 |
|
3,684 |
4,683 |
4,144 |
|
2,549 |
3,121 |
2,689 |
|
3,692 |
4,728 |
4,004 |
|
2,549 |
3,095 |
2,663 |
|
3,681 |
4,461 |
4,084 |
|
2,549 |
3,134 |
2,682 |
|
3,685 |
4,609 |
3,948 |
|
|
|
|
|
|
|
|
Obliczenia:
Obliczenie wartości C dla h= 0,46
![]()
Kulka 1
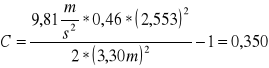
Kulka 2
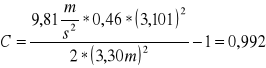
Kulka 3
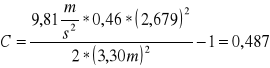
Obliczenie wartości C dla h= 0,23
Kulka 1
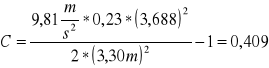
Kulka 2
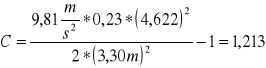
Kulka 3
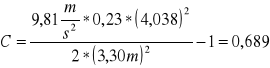
Obliczenie wartości momentu bezwładności I: dla h= 0,46
Kulka 1
![]()
![]()
![]()
![]()
![]()
![]()
Kulka 2
![]()
![]()
![]()
![]()
![]()
![]()
Kulka 3
![]()
![]()
![]()
![]()
![]()
![]()
dla h= 0,23
Kulka 1
![]()
![]()
![]()
![]()
![]()
![]()
Kulka 2
![]()
![]()
![]()
![]()
![]()
![]()
Kulka 3
![]()
![]()
![]()
![]()
![]()
![]()
Szacowanie niepewności pomiaru uwzględniając niepewność wzorcowania i eksperymentatora
Niepewność pomiarowa u(h)
![]()
![]()
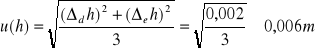
Niepewność pomiarowa u(m)
![]()
![]()
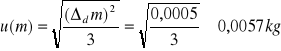
Niepewność pomiarowa u(R)
![]()
![]()
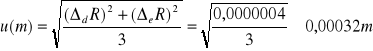
Niepewność standardowa
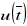
dla każdej kulki
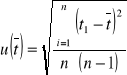
Rachunek niepewności pomiarowych dla kuli 1 toczonej z wysokości h1.
L.p. |
t |
|
|
|
1 |
2,557 |
2,553 |
0,004 |
0,000016 |
2 |
2,558 |
2,553 |
0,005 |
0,000025 |
3 |
2,549 |
2,553 |
-0,004 |
0,000016 |
4 |
2,567 |
2,553 |
0,014 |
0,000196 |
5 |
2,553 |
2,553 |
0 |
0 |
6 |
2,553 |
2,553 |
0 |
0 |
7 |
2,553 |
2,553 |
0 |
0 |
8 |
2,549 |
2,553 |
-0,004 |
0,000016 |
9 |
2,549 |
2,553 |
-0,004 |
0,000016 |
10 |
2,549 |
2,553 |
-0,004 |
0,000016 |
|
0,000301 |
|||
![]()
Rachunek niepewności pomiarowych dla kuli 2 toczonej z wysokości h1.
L.p. |
t |
|
|
|
1 |
3,068 |
3,101 |
-0,033 |
0,001089 |
2 |
3,045 |
3,101 |
0,056 |
0,003136 |
3 |
3,090 |
3,101 |
-0,011 |
0,000121 |
4 |
3,129 |
3,101 |
0,028 |
0,000784 |
5 |
3,134 |
3,101 |
0,033 |
0,001089 |
6 |
3,114 |
3,101 |
0,013 |
0,000169 |
7 |
3,083 |
3,101 |
-0,018 |
0,000324 |
8 |
3,121 |
3,101 |
0,02 |
0,000400 |
9 |
3,095 |
3,101 |
0,006 |
0,000036 |
10 |
3,134 |
3,101 |
0,033 |
0,001089 |
|
0,008237 |
|||
![]()
Rachunek niepewności pomiarowych dla kuli 3 toczonej z wysokości h1.
L.p. |
t |
|
|
|
1 |
2,703 |
2,679 |
0,024 |
0,000576 |
2 |
2,671 |
2,679 |
-0,008 |
0,000640 |
3 |
2,687 |
2,679 |
0,008 |
0,000640 |
4 |
2,657 |
2,679 |
-0,022 |
0,000484 |
5 |
2,681 |
2,679 |
0,002 |
0,000004 |
6 |
2,662 |
2,679 |
-0,017 |
0,000289 |
7 |
2,695 |
2,679 |
0,016 |
0,000256 |
8 |
2,689 |
2,679 |
0,010 |
0,000100 |
9 |
2,663 |
2,679 |
-0,016 |
0,000256 |
10 |
2,682 |
2,679 |
0,003 |
0,000009 |
|
0,003254 |
|||
![]()
Rachunek niepewności pomiarowych dla kuli 1 toczonej z wysokości h2.
L.p. |
t |
|
|
|
1 |
3,687 |
3,688 |
0,001 |
0,000001 |
2 |
3,681 |
3,688 |
-0,007 |
0,000049 |
3 |
3,686 |
3,688 |
-0,002 |
0,000004 |
4 |
3,709 |
3,688 |
0,021 |
0,000441 |
5 |
3,700 |
3,688 |
0,012 |
0,000144 |
6 |
3,682 |
3,688 |
-0,006 |
0,000036 |
7 |
3,684 |
3,688 |
-0,004 |
0,000016 |
8 |
3,692 |
3,688 |
0,004 |
0,000016 |
9 |
3,681 |
3,688 |
-0,007 |
0,000049 |
10 |
3,685 |
3,688 |
-0,003 |
0,000009 |
|
0,000765 |
|||
![]()
Rachunek niepewności pomiarowych dla kuli 2 toczonej z wysokości h2.
L.p. |
t |
|
|
|
1 |
4,594 |
4,622 |
-0,028 |
0,000784 |
2 |
4,743 |
4,622 |
0,121 |
0,014641 |
3 |
4,649 |
4,622 |
0,027 |
0,000729 |
4 |
4,584 |
4,622 |
-0,038 |
0,001444 |
5 |
4,567 |
4,622 |
-0,055 |
0,003025 |
6 |
4,603 |
4,622 |
-0,019 |
0,000361 |
7 |
4,683 |
4,622 |
0,061 |
0,003721 |
8 |
4,728 |
4,622 |
0,106 |
0,011236 |
9 |
4,461 |
4,622 |
-0,161 |
0,025921 |
10 |
4,609 |
4,622 |
-0,013 |
0,000169 |
|
0,062031 |
|||
![]()
Rachunek niepewności pomiarowych dla kuli 3 toczonej z wysokości h2.
L.p. |
t |
|
|
|
1 |
4,104 |
4,038 |
0,066 |
0,004356 |
2 |
3,948 |
4,038 |
-0,090 |
0,008100 |
3 |
4,134 |
4,038 |
0,096 |
0,009216 |
4 |
3,949 |
4,038 |
-0,089 |
0,001921 |
5 |
4,074 |
4,038 |
0,036 |
0,001296 |
6 |
3,993 |
4,038 |
-0,045 |
0,002025 |
7 |
4,144 |
4,038 |
0,106 |
0,011236 |
8 |
4,004 |
4,038 |
-0,034 |
0,001156 |
9 |
4,084 |
4,038 |
0,046 |
0,002116 |
10 |
3,948 |
4,038 |
-0,090 |
0,008100 |
|
0,049522 |
|||
![]()
Niepewność pomiarowa u(C)
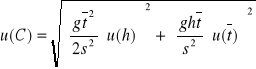
dla wysokości h = 0,46
kulka 1
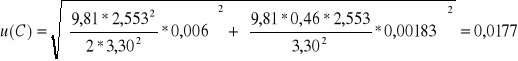
kulka 2
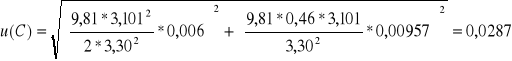
kulka 3
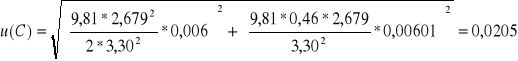
dla wysokości h = 0,23
kulka 1
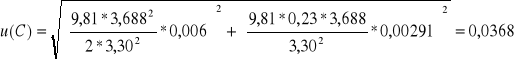
kulka 2
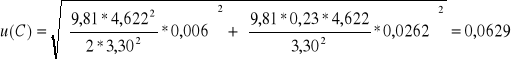
kulka 3
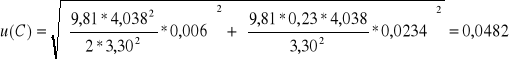
Niepewność pomiarowa u(Id)
dla wysokości h = 0,46
kulka 1
![]()
kulka 2
![]()
kulka 3
![]()
dla wysokości h = 0,23
kulka 1
![]()
kulka 2
![]()
kulka 3
![]()
Wyniki wszystkich obliczeń przedstawia poniższa tabela
Dla kulki 1 na wysokości 0,46 m i promieniu 2,05cm
Dla kulki 2 na wysokości 0,46 m i promieniu 1,85cm
Dla kulki 3 na wysokości 0,46 m i promieniu 1,35cm
Dla kulki 1 na wysokości 0,23 m i promieniu 2,05cm
Dla kulki 2 na wysokości 0,23 m i promieniu 1,85cm
Dla kulki 3 na wysokości 0,23 m i promieniu 1,35cm
Wnioski :
Celem naszego doświadczenia było wyznaczenia momentu bezwładności I bryły sztywnej. Po wykonaniu ćwiczenia i obliczeniach można stwierdzić że, momenty bezwładności kul wyznaczone doświadczalnie nieznacznie różnią się od momentów bezwładności kul wyliczonych teoretycznie. Spowodowane jest to pewną różnicą współczynnika C wyznaczonego doświadczalnie od teoretycznego współczynnika C ze wzoru na moment bezwładności I=C*m*R , który wynosi 2/5 dla kuli pełnej i 2/3 dla kuli wydrążonej cienkościennej.. Na tą różnicę mają wpływ błędy pomiarowe takie jak: błąd pomiaru masy kuli, błąd pomiaru promienia kuli.
|
h = 0,46 |
||
|
Kulka 1 |
Kulka 2 |
Kulka 3 |
C |
0,350 |
0,992 |
0,487 |
m [kg] |
0,286 |
0,00263 |
0,0787 |
R [m] |
0,0205 |
0,0185 |
0,0135 |
|
|
|
|
|
|
|
|
|
h = 0,23 |
||
|
Kulka 1 |
Kulka 2 |
Kulka 3 |
C |
0,409 |
1,213 |
0,689 |
m [kg] |
0,286 |
0,00263 |
0,0787 |
R [m] |
0,0205 |
0,0185 |
0,0135 |
|
|
|
|
|
|
|
|
Porównanie wartości doświadczalnej z wartością teoretyczna
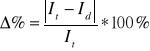
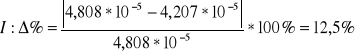
![]()
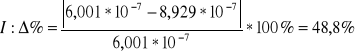
![]()
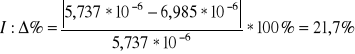
![]()
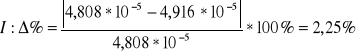
![]()
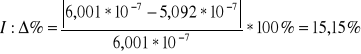
![]()
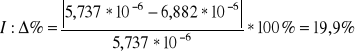
![]()
Wyszukiwarka