RENTA

1. Wartość przyszła renty

Wartością przyszłą renty FVA (renty z góry FVA_D) jest taka kwota na końcu ostatniego odcinka czasu, że jest ona równoważna serii płatności przy danym oprocentowaniu oraz danej liczbie okresów.

Oznaczmy przez PMT płatności renty dla i = 1, 2,..., n, gdzie n oznacza liczbę płatności. Płatności są dokonywane na końcu każdego odcinka czasu, a więc odcinków czasu jest również n, ponumerowanych od 1 do n. Natomiast chwil czasu jest (n+1), ponieważ pierwszy odcinek czasu rozpoczyna się w chwili zerowej i kończy w chwili pierwszej. Wartość obecna renty obliczana w chwili n (na końcu n-tego odcinka czasu) jest sumą wartości przyszłych każdej z płatności PMT. Oznaczając przez FV(PMT, i) wartość przyszłą w chwili n płatności dokonanej w chwili i-tej można zapisać (rys. Błąd! W dokumencie nie ma tekstu o podanym stylu..10, Błąd! W dokumencie nie ma tekstu o podanym stylu..11)

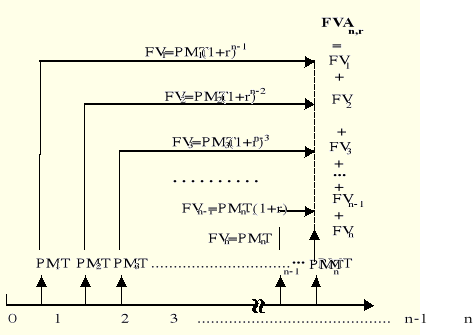
Rys. Błąd! W dokumencie nie ma tekstu o podanym stylu..1. Proces obliczania wartości przyszłej kapitału gromadzonego przez n okresów

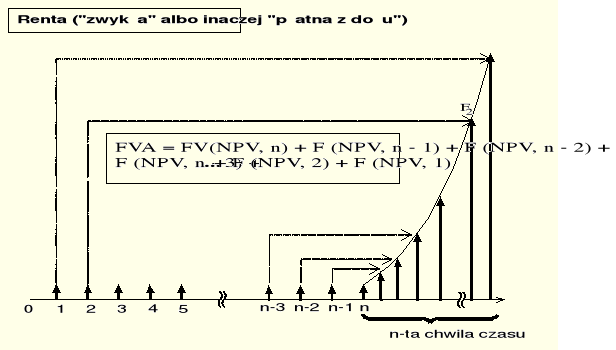
Rys..Błąd! W dokumencie nie ma tekstu o podanym stylu..2. Wartość przyszła renty.

FVA = FV(PMT, n) + FV(PMT, n-1) +... + FV(PMT, 2) + FV(PMT, 1) (Błąd! W dokumencie nie ma tekstu o podanym stylu..1)

Ze wzoru Błąd! W dokumencie nie ma tekstu o podanym stylu..5

FV(PMT, n) = PMT*(1+r)⁰ = PMT*1 = PMT,

FV(PMT, n−1) = PMT*(1+r)¹, wartość PMT z chwili (n−1) podlega oprocentowaniu przez jeden okres,

FV(PMT, 2) = PMT*(1+r)ⁿ⁻² wartość PMT z chwili drugiej podlega oprocentowaniu przez (n−2) okresy,

FV(PMT, 1) = PMT*(1+r)ⁿ⁻¹ wartość PMT z chwili pierwszej podlega oprocentowaniu przez (n−1) okresów.

Podstawiając 4 ostatnie obliczenia do wzoru Błąd! W dokumencie nie ma tekstu o podanym stylu..22 otrzymamy

FVA = PMT + PMT*(1+r)¹ +... + PMT*(1+r)ⁿ⁻² +PMT*(1+r)ⁿ⁻¹. (Błąd! W dokumencie nie ma tekstu o podanym stylu..22a)

Dokonamy teraz dwu różnych przekształceń wzoru Błąd! W dokumencie nie ma tekstu o podanym stylu..22a i przyrównamy do siebie wyniki obu przekształceń.

Przekształcenie A

Obie strony mnożymy przez (1+r), a następnie dodajemy do obu PMT

FVA*(1+r) + PMT=
= [PMT + PMT*(1+r)¹ +... + PMT*(1+r)ⁿ⁻² +PMT*(1+r)ⁿ⁻¹]*(1+r) + PMT.

Otwieramy z prawej strony nawias kwadratowy co powoduje, że rosną potęgi wyrazów (1+r)

FVA*(1+r) + PMT=
= PMT*(1+r) + PMT*(1+r)² +... + PMT*(1+r)ⁿ⁻¹ +PMT*(1+r)ⁿ + PMT.

Porządkujemy równanie przenosząc ostatni wyraz PMT na początek

FVA*(1+r) + PMT=
=PMT + PMT*(1+r) + PMT*(1+r)² +... + PMT*(1+r)ⁿ⁻¹ +PMT*(1+r)ⁿ. (Błąd! W dokumencie nie ma tekstu o podanym stylu..2A)

Przekształcenie B

Do obu stron wzoru Błąd! W dokumencie nie ma tekstu o podanym stylu..22a dodajemy PMT*(1+r)ⁿ:

FVA + PMT*(1+r)ⁿ =
PMT + PMT*(1+r)¹ +... + PMT*(1+r)ⁿ⁻² + PMT*(1+r)ⁿ⁻¹ + PMT*(1+r)ⁿ (Błąd! W dokumencie nie ma tekstu o podanym stylu..23B)

Prawe strony wzorów Błąd! W dokumencie nie ma tekstu o podanym stylu..23A i Błąd! W dokumencie nie ma tekstu o podanym stylu..23B są identyczne, wobec tego i lewe muszą się sobie równać:

FVA*(1+r) + PMT = FVA + PMT*(1+r)ⁿ.

Otwieramy z lewej strony nawias:

FVA+ FVA*r + PMT = FVA + PMT*(1+r)ⁿ.

Odejmujemy od obu stron FVA oraz PMT

FVA*r = PMT*(1+r)ⁿ − PMT.

Z prawej strony wyciągamy przed nawias PMT, a następnie obie strony dzielimy przez r i uzyskujemy ostateczną postać wzoru na wartość przyszłą renty płatnej z dołu:

. (Błąd! W dokumencie nie ma tekstu o podanym stylu..3)

Wzór można przedstawić również z pomocą mnożnika wartości przyszłej dla renty
:

, gdzie (Błąd! W dokumencie nie ma tekstu o podanym stylu..24a)

. (Błąd! W dokumencie nie ma tekstu o podanym stylu..24b)

Wartość
jest stablicowana na końcu książki.

2. Wartość obecna renty

Wartością obecną renty PVA (PVA_D dla płatnej renty z góry) jest taka kwota w chwili 0, że jest ona równoważna serii płatności przy danym oprocentowaniu i danej liczbie okresów.

Skoro obliczyliśmy wartość przyszłą, to łatwo można teraz obliczyć wartość obecną renty płatnej z dołu korzystając ze wzoru Błąd! W dokumencie nie ma tekstu o podanym stylu..9. Ponieważ mamy do czynienia z rentą, oznaczmy we wzorze Błąd! W dokumencie nie ma tekstu o podanym stylu..9 wartość obecną przez PVA zamiast PV oraz FVA zamiast FV. Wówczas otrzymamy:

oraz podstawiając za FVA wartość ze wzoru Błąd! W dokumencie nie ma tekstu o podanym stylu..24 mamy:

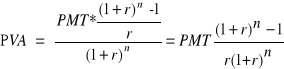
(Błąd! W dokumencie nie ma tekstu o podanym stylu..4)

lub rozbijając ułamek na różnicę dwu ułamków

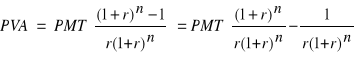
otrzymujemy ostatecznie

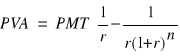
(Błąd! W dokumencie nie ma tekstu o podanym stylu..5)

Wzór można przedstawić również z pomocą mnożnika wartości obecnej dla renty
:

, gdzie (Błąd! W dokumencie nie ma tekstu o podanym stylu..26a)

. (Błąd! W dokumencie nie ma tekstu o podanym stylu..26b)

Wartość
jest stablicowana na końcu książki.

3. Wnioski

Wniosek D

Jeśli mamy dwie renty o tym samym oprocentowaniu r i tej samej liczbie okresów n, to jeśli płatności A pierwszej renty są X razy większe od płatności B drugiej renty, to również wartość przyszła pierwszej renty PVA(A) jest X razy większa od wartości przyszłej drugiej renty PVA(B):

FVA(A) =
=
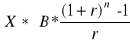
= X*FVA(B). (Błąd! W dokumencie nie ma tekstu o podanym stylu..6D)

Wniosek E

Jeśli mamy dwie renty o tym samym oprocentowaniu r i tej samej liczbie okresów n, to jeśli płatności A pierwszej renty są X razy większe od płatności B drugiej renty, to również wartość obecna pierwszej renty PVA(A) jest X razy większa od wartości obecnej drugiej renty PVA(B):

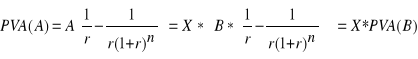
(Błąd! W dokumencie nie ma tekstu o podanym stylu..27E)

Przykład Błąd! W dokumencie nie ma tekstu o podanym stylu..1.

Ile powinien wpłacić Pan Adam do banku dziś, aby w następnych kolejnych latach otrzymywać wypłaty w wysokości 2 000 zł rocznie przez nieograniczony okres czasu, jeśli zakłada się, ze stopa procentowa będzie stała r=15%?. Albo, inaczej mówiąc, jaka kwota wpłacona dziś, zrównoważy konieczność dokonywania wpłat przez nieograniczony okres czasu w wysokości 2 000 zł.?

Rozwiązanie sprowadza się do obliczenia wartości obecnej renty wiecznej, rys. Błąd! W dokumencie nie ma tekstu o podanym stylu..13.

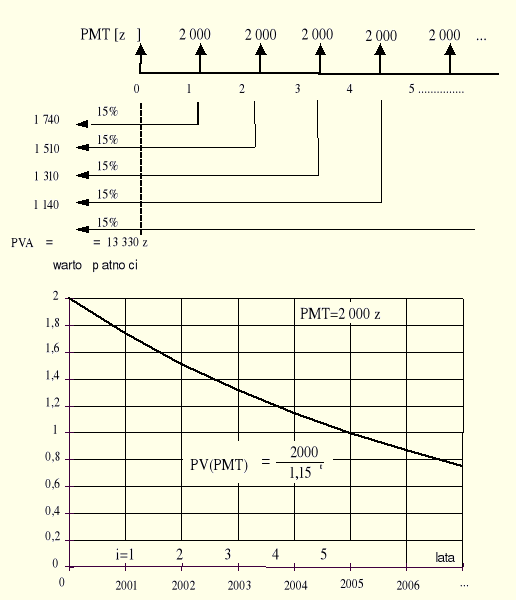
Rys..Błąd! W dokumencie nie ma tekstu o podanym stylu..3. Proces obliczania PVA (2 000 zł) dla renty wiecznej.

Przykład Błąd! W dokumencie nie ma tekstu o podanym stylu..2.

Ile powinien wpłacić Pan Adam do banku dziś, aby w następnych kolejnych latach otrzymywać wypłaty rosnące o 12% rocznie w stosunku do obecnej wartości 2 000 zł przez nieograniczony okres czasu, jeśli zakłada się, ze stopa procentowa będzie stała r=15%?. Inaczej mówiąc, jaka kwota wpłacona dziś, zrównoważy konieczność dokonywania rosnących o 12% rocznie wpłat przez nieograniczony okres czasu, przy obecnej wartości wpłaty równej 2 000 zł.?

Rozwiązanie sprowadza się do obliczenia wartości obecnej renty wiecznej, rys Błąd! W dokumencie nie ma tekstu o podanym stylu..15.

,

gdzie g - stopa wzrostu płatności (12%).

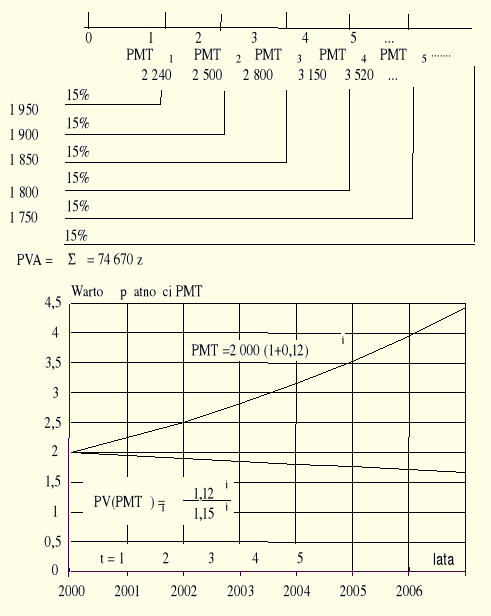
Rys..Błąd! W dokumencie nie ma tekstu o podanym stylu..4. Proces obliczania wartości obecnej renty wiecznej przy wzrastających płatnościach.

2. Spłata pożyczek

Istnieje wiele sposobów rozłożenia spłaty rat i odsetek pożyczki w czasie. Leży to w gestii umawiających się stron, najczęściej banku i jego klienta. O ile niegdyś banki polskie stosowały sztywne umowy kredytowe, to współcześnie są bardzo elastyczne i sposób spłaty (amortyzacji) pożyczki może zostać przykrojony do potrzeb klienta, na przykład, jego różnej możliwości spłat w ciągu roku z powodu sezonowego charakteru produkcji i sprzedaży.

Negocjacji, poza stopą procentową, prowizją, wysokością kredytu, liczbą spłat, czasem i wysokością transz (częściowe wypłaty kredytu), sposobem zabezpieczenia spłaty i celem wykorzystania kredytu podlegają:

1. karencja (termin pierwszej spłaty),

2. czy w okresie karencji odsetki mają być regularnie spłacane, czy też mają być kapitalizowane (dopisywane do podstawowej kwoty kredytu),

3. częstość spłat rat pożyczki (co miesiąc, co kwartał, co roku czy też inaczej),

4. czy raty spłaty kwoty podstawowej kredytu (kapitału) mają być równe, czy też suma raty i odsetek spłacanych przy danej racie ma być stała.

W tym rozdziale zostaną omówione dwa najbardziej popularne sposoby amortyzacji pożyczki, to znaczy:

1. spłata pożyczki równymi ratami i bieżącymi (nierównymi) odsetkami (sposób znany jako spłata równymi ratami kapitałowymi),

2. spłata pożyczki różnymi ratami i bieżącymi odsetkami, tak aby suma danej raty spłaty kapitału i bieżących odsetek była stała (sposób znany jako spłata stałą kwotą sumy raty i odsetek).

Dla uproszczenia założymy, że:

a) kredyt jest pobierany w całości (jedną transzą),

b) nie ma karencji kredytu,

c) spłaty rat są stałe i następują co stały okres,

d) oprocentowanie kredytu za każdy okres wynosi r,

e) odsetki spłacane są „na bieżąco” przy spłacie raty kapitału pożyczki.

Najpierw omówimy bardziej znany, pierwszy sposób.

1. Spłata kredytu równymi ratami kapitałowymi

Ponieważ wszystkie raty są równe, więc

, gdzie: (Błąd! W dokumencie nie ma tekstu o podanym stylu..7)

R_i − kwota spłaty i-tej raty,

R_i = R, dla i = 1, 2,...n (wszystkie raty są równe)

K − kwota pożyczonego kapitału,

n − liczba rat równa liczbie okresów spłaty.

Natomiast odsetki I_i spłacane na koniec i-tego okresu są zależne od salda kredytu K_i w i-tym okresie:

I_i = K_i*r, (Błąd! W dokumencie nie ma tekstu o podanym stylu..33a)

K₁ = K,

K_i = K − (i − 1)* R_{i − 1} = K − (i − 1)* R, czyli (Błąd! W dokumencie nie ma tekstu o podanym stylu..33b)

I_i = [K − (i − 1)* R]*r . (Błąd! W dokumencie nie ma tekstu o podanym stylu..33c)

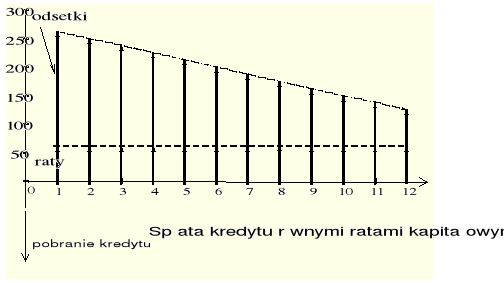
Rys. Błąd! W dokumencie nie ma tekstu o podanym stylu..5. Spłata kredytu − r = 20% w okresie, kwota kredytu = 1 000, 12 rat.

2. Spłata kredytu stałą kwotą sumy raty i odsete

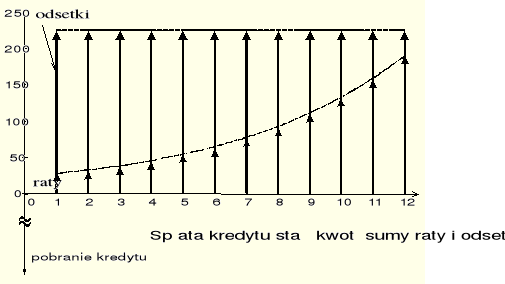
Rys. Błąd! W dokumencie nie ma tekstu o podanym stylu..6. Spłata kredytu − r = 20% w okresie, kwota kredytu = 1 000, 12 rat. Widać początkowo bardzo małe kwoty raty i olbrzymie odsetki. Z kolei pod koniec spłacania kredytu zanikają odsetki, a prawie całą kwotę płatności tworzy rata kapitałowa.

Taki sposób spłacania kredytu to po prostu renta zwykła, co ilustruje rysunek Błąd! W dokumencie nie ma tekstu o podanym stylu..16. Aby ustalić wielkość równych kwot sumy raty i odsetek, korzysta się więc z wzoru na wartość obecną renty:

⇒

⇒
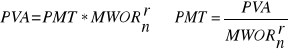
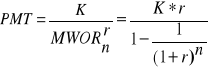
(Błąd! W dokumencie nie ma tekstu o podanym stylu..8)

gdzie: PVA = K (kwota kredytu),

PMT = R_i + I_i,

I_i, − kwota odsetek w i-tym okresie.

I₁ = r*K, K₁ = K,

odsetki w i-tym okresie I_i = r* K_i,
kwota raty w i-tym okresie R_i = PMT − I_i,
natomiast saldo kredytu w i-tym okresie

, (Błąd! W dokumencie nie ma tekstu o podanym stylu..9)

ponieważ saldo w i-tym okresie jest rentą pozostałych jeszcze płatności w liczbie (n − i +1), tak jak kwota kredytu czyli saldo w 1-ym okresie jest rentą pozostałych jeszcze (n − 1 +1) = n płatności. Stąd ostatecznie odsetki w i−tym okresie wynoszą

,

natomiast pozostałą część całej płatności stanowi rata kapitałowa

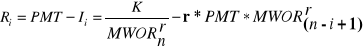
(Błąd! W dokumencie nie ma tekstu o podanym stylu..10)

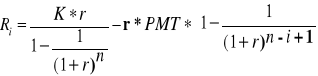
(Błąd! W dokumencie nie ma tekstu o podanym stylu..36a)

Przykład Błąd! W dokumencie nie ma tekstu o podanym stylu..3.

Spółka TOR S.A. zaciągnęła pięcioletni kredyt bankowy w wysokości 18 000 000 zł. Oprocentowanie kredytu w skali roku wynosi 20%. Menedżer finansowy spółki przeprowadza analizę amortyzacji kredytu dwoma sposobami.

Wpłaty równymi ratami kapitałowymi plus odsetki (wpłaty nierówne).

Wpłaty równe - raty kapitałowe plus odsetki tworzą równe kwoty.

Tabela Błąd! W dokumencie nie ma tekstu o podanym stylu..1 oraz rysunek Błąd! W dokumencie nie ma tekstu o podanym stylu..17 przedstawiają amortyzację kredytu spłacanego równymi ratami kapitałowymi

Tab. Błąd! W dokumencie nie ma tekstu o podanym stylu..1. Amortyzacja kredytu równymi ratami kapitałowymi.

	Okres	Rata kapitałowa	Odsetki	Wpłata	Stan kredytu
	0				18 000 000
	1	3 600 000	3 600 000	7 200 000	14 400 000
	2	3 600 000	2 880 000	6 480 000	10 800 000
	3	3 600 000	2 160 000	5 760 000	7 200 000
	4	3 600 000	1 440 000	5 040 000	3 600 000
	5	3 600 000	720 000	4 320 000	0
	SUMA	18 000 000	10 800 000	28 800 000

Wartość pięcioletnich odsetek wynosi 10 800 000 zł.

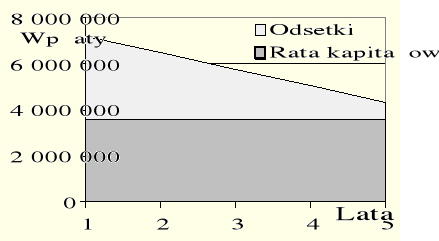
Rys..Błąd! W dokumencie nie ma tekstu o podanym stylu..7. Spłaty kredytu równymi ratami kapitałowymi.

Amortyzację kredytu równymi wpłatami przedstawia tabela Błąd! W dokumencie nie ma tekstu o podanym stylu..2 oraz rysunek Błąd! W dokumencie nie ma tekstu o podanym stylu..18.

Kwotę równych wpłat obliczyć można ze wzoru na wartość obecną renty

Wartość mnożnika dla renty 5-letniej i 20% oprocentowania wynosi 2,9906, wówczas

Tab. Błąd! W dokumencie nie ma tekstu o podanym stylu..2. Amortyzacja kredytu równymi wpłatami.

	Okres	Rata kapitałowa	Odsetki	Wpłata	Stan kredytu
	0				18 000 000
	1	2 418 859	3 600 000	6 018 859	15 581 141
	2	2 902 631	3 116 228	6 018 859	12 678 510
	3	3 483 157	2 535 702	6 018 859	9 195 353
	4	4 179 789	1 839 071	6 018 859	5 015 564
	5	5 015 564	1 003 113	6 018 859	0
	SUMA	18 000 000	12 094 114	30 094 295

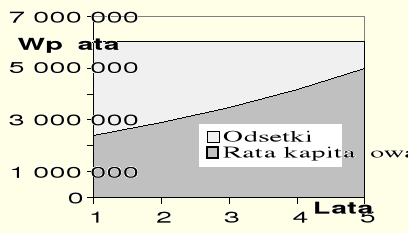
Rys. Błąd! W dokumencie nie ma tekstu o podanym stylu..8. Spłaty kredytu równymi wpłatami.

Wartość odsetek wpłaconych wciągu 5 lat wynosi 12 094 114 zł.

Pozornie sposób drugi wydaje się droższy. Ale tylko pozornie - pożyczony kapitał spłacany jest wolniej, (rys. Błąd! W dokumencie nie ma tekstu o podanym stylu..19.).

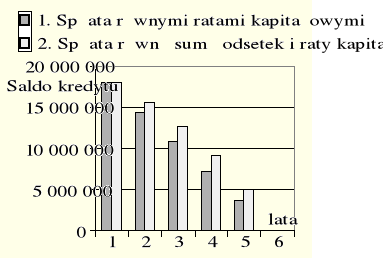
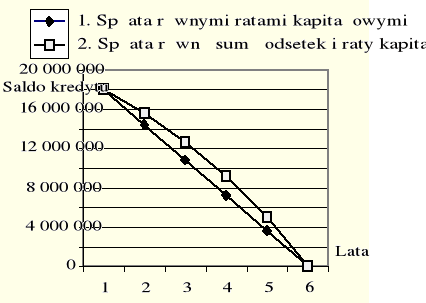
Rys. Błąd! W dokumencie nie ma tekstu o podanym stylu..9. Stan kredytu w kolejnych latach w różnych formach płatności.

Przykład Błąd! W dokumencie nie ma tekstu o podanym stylu..4.

Pan Adam osiągnie wiek emerytalny za n lat. Postanowił przez te lata wpłacać na swoje konto osobiste kwoty w wysokości PMT₁, PMT₂,..., PMT_n rocznie, aby przez następne m. lat móc otrzymywać emeryturę roczną w kwocie EMT₁, EMT₂,..., EMT_m.

W jakiej sytuacji pan Adam może się spodziewać, że jego oczekiwania zostaną zrealizowane? Pan Adam zakłada, że w całym rozważanym okresie 1,..., n+m. lat stopa procentowa będzie taka sama.

Rozważaną sytuację przedstawia rysunek Błąd! W dokumencie nie ma tekstu o podanym stylu..20.

Wynika z niej, że wartość przyszła kapitału na koniec roku n-tego FVA_n.r powinna być równa wartości obecnej kapitału wypłaconego w latach n+1 do n+m., czyli PVA_m,r.

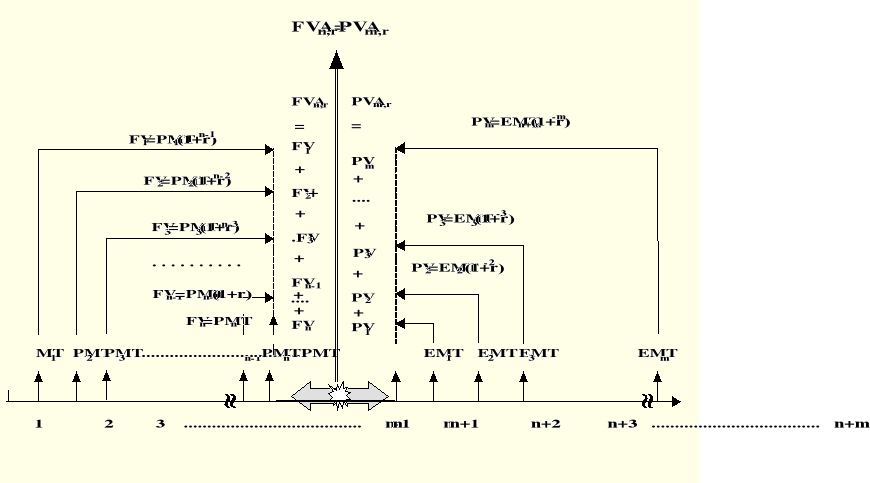
Rys. Błąd! W dokumencie nie ma tekstu o podanym stylu..10. Proces obliczania równowagi między rocznymi składkami a rocznymi wypłatami.

Kapitalizacja - wartość obecna

Rozważmy najpierw sytuację inwestora długoterminowego kupującego akcje z zamiarem trzymania ich w nieskończoność - oczekującego dochodu tylko w formie wypłacanych mu corocznie dywidend. W tej sytuacji wychodząc z określenia ceny akcji P0 jako nieskończonej sumy zdyskontowanych dywidend (6.3) i podstawiając za Dt wyrażenie (6.6) otrzymuje się

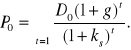
(Błąd! W dokumencie nie ma tekstu o podanym stylu..11)

Oznaczmy

(Błąd! W dokumencie nie ma tekstu o podanym stylu..12)

Jeśli ks > g, to 1+h< 1 i wówczas wykorzystując wzór na sumę skumulowanych strumieni gotówki otrzymujemy

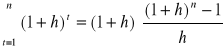
. (Błąd! W dokumencie nie ma tekstu o podanym stylu..13)

Granica (6.9) przy n wynosi

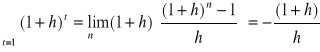
. (Błąd! W dokumencie nie ma tekstu o podanym stylu..14)

Biorąc pod uwagę wyrażenie (6.8), otrzymujemy

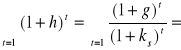
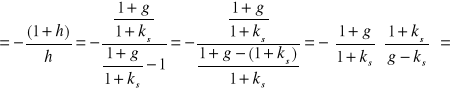
(Błąd! W dokumencie nie ma tekstu o podanym stylu..15)

Wstawiając teraz wyrażenie (6.10) do (6.11), otrzymujemy

(Błąd! W dokumencie nie ma tekstu o podanym stylu..16)

Zatem cena akcji, jaką potencjalny inwestor jest skłonny zapłacić w chwili t = 0 przy żądanej stopie zwrotu ks i prognozowanej stopie wzrostu firmy g jest równa stosunkowi oczekiwanej dywidendy roku przyszłego t = 1 oraz różnicy między żądaną stopą zwrotu i stopą wzrostu firmy. Ma więc wartość renty wiecznej o płatności rocznej D1 i stopie dyskontowej r = ks - gs, czyli mniejszej o g od żądanej stopy zwrotu k_s.

Należy podkreślić, że wyrażenie (6.12) jest słuszne wtedy i tylko wtedy, gdy ks > g;

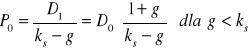
W przypadku k_s * g wyrażenie (6.11) traci sens, ponieważ jest ono słuszne tylko w tym przypadku, gdy zachodzi (6.9).

Dla g = ks, tzn. gdy stopa wzrostu i żądana stopa zwrotu akcjonariusza są sobie równe zachodzi

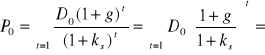
Analogicznie w przypadku, gdy g > ks;

ponieważ g > ks, a więc 1 + g > 1 + ks oraz h > 0, stąd

.

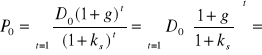
W sytuacji, gdy inwestor kupuje akcje z zamiarem sprzedania ich po upływie n lat, cena akcji P0, jaką jest on skłonny zapłacić w chwili t = 0 przy żądanej stopie zwrotu ks oraz stopie wzrostu firmy (w sensie zysku netto i dywidendy) g < ks, zgodnie ze wzorem (6.2) oraz (6.12) wynosi

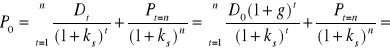
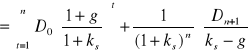
, (Błąd! W dokumencie nie ma tekstu o podanym stylu..17)

albo przy oznaczeniu

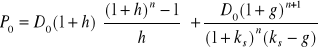
, (Błąd! W dokumencie nie ma tekstu o podanym stylu..18)

czyli składa się z dwu składników

- skończonej sumy zdyskontowanych strumieni dywidend z n okresów oraz

- zdyskontowanej (stopa dyskontowa jest równa ks) przez n okresów oczekiwanej ceny akcji w chwili t = n, która zgodnie z (6.12) wynosi

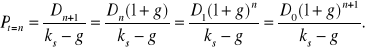
, dla g < k_s. (Błąd! W dokumencie nie ma tekstu o podanym stylu..19)

Jeżeli stopa wzrostu g
ks, zachodzi:

dla g = ks

dla g > ks

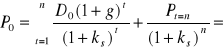
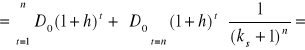
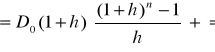
W obu przypadkach, inwestycji długoterminowych i krótkoterminowych, w sytuacji gdy

• przewidywana stopa wzrostu firmy jest stała i

• inwestor godzi się zarobić mniej, niż prognozowany poziom stopy wzrostu firmy k_s < g, a

• z polityki firmy dotyczącej wypłaty dywidend wynika, że udział wypłaconych dywidend w zysku netto jest stały,
  = const;

cena akcji P₀ jaką może zapłacić potencjalny inwestor wynika tylko z kompromisu będącego wynikiem negocjacji między sprzedającym i kupującym. Z rozważanego modelu dywidendowego wynika bowiem, że cena akcji powinna być nieskończenie wysoka, co oczywiście w praktyce jest sytuacją nierealną.

W sytuacji, gdy stopa wzrostu firmy przekracza żądaną stopę zwrotu inwestora, g₁>k_s, ale tylko w początkowym okresie dla t
{1,2,..., n}, czyli od momentu zakupienia akcji aż do chwili t = n, a następnie przewiduje się stałą stopę wzrostu g₂<k_s, to cenę akcji można wyznaczyć w następujący sposób:

zgodnie z (6.12)

,

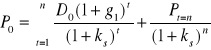
cenę akcji w przypadku, gdy g < k_s zgodnie ze wzorem (6.12) wyznacza się jako
. Zatem można napisać, że
. Ponieważ D_n+1 = D_n(1+g), a w rozważanym przypadku do momentu t = n stopa wzrostu wynosi g₁, a w okresie t = n+1 obowiązuje już stopa wzrostu g₂, to D_n+1 = D_n(1+g₂), gdzie D_n = D₀(1+g₁).

Stąd

Zatem

. (Błąd! W dokumencie nie ma tekstu o podanym stylu..20)

W podobny sposób wyznaczyć można cenę akcji P₀ w sytuacji, gdy inwestor rozważa zakup akcji o nierównomiernie zmieniającej się stopie wzrostu firmy, przy założeniu jednak, że końcowa stopu wzrostu będzie stała i mniejsza od żądanej stopy zwrotu akcjonariusza.

Rozważając stopę wzrostu firmy (w sensie wzrostu zysku netto) rozważa się następujące sytuacje

1. malejący zysk netto firmy, stopa wzrostu g < 0,

2. zerowy wzrost firmy (zysk netto = constans), stopa wzrostu g = 0,

3. stały lub normalny wzrost firmy, stopa wzrostu g > 0, ale g < ks,

4. supernormalny wzrost firmy, stopa wzrostu gs > 0, rzędu kilkunastu procent rocznie, ale gs < ks,

5. niestały wzrost firmy: supernormalny wzrost w początkowym skończonym okresie, stopa wzrostu gs niekoniecznie musi być mniejsze od stopy ks, a następnie wzrost normalny gn < gs i z warunkiem gn < ks,.

10

13

---