Teoria Maszyn i Mechanizmów
Analiza Mechanizmu:
Krzysztof Batko
Gr. 16A
Rok akad. 2007/2008
Wymiary mechanizmu:
|AB|=0,1[m]
|BC|=0,05[m]
|OC|=0,15[m]
|BD|=0,05 [m]
Dane:
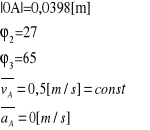
Grafoanalityczne wyznaczanie prędkości mechanizmu.
Zgodnie z przyjętą prędkością członu napędzającego, prędkość ![]()
=0,5[m/s].
Aby wyznaczyć prędkość punktu B należy zapisać równanie:
![]()
.
Człon 2 porusza się ruchem złożonym więc ![]()
to prędkość unoszenia, a ![]()
to prędkość ruchu względnego (ruch obrotowy wokół punktu A). Podwójne podkreślenie wektora oznacza, że znamy kierunek i wartość wektora; pojedyncze oznacza, że znamy jedynie kierunek wektora. Wektor ![]()
jest równoległy do |OA|, a ![]()
jest prostopadły do członu 2.
Dla punktu D możemy zapisać:
![]()
![]()
![]()
![]()
Wektor prędkości ![]()
jest prostopadły do |DA|
Wyznaczanie prędkości środka masy
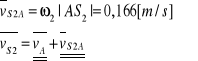
Podziałka rysunkowa dla planu prędkości:![]()
.
Na podstawie powyższych obliczeń można utworzyć plan prędkości (w programie AutoCAD):
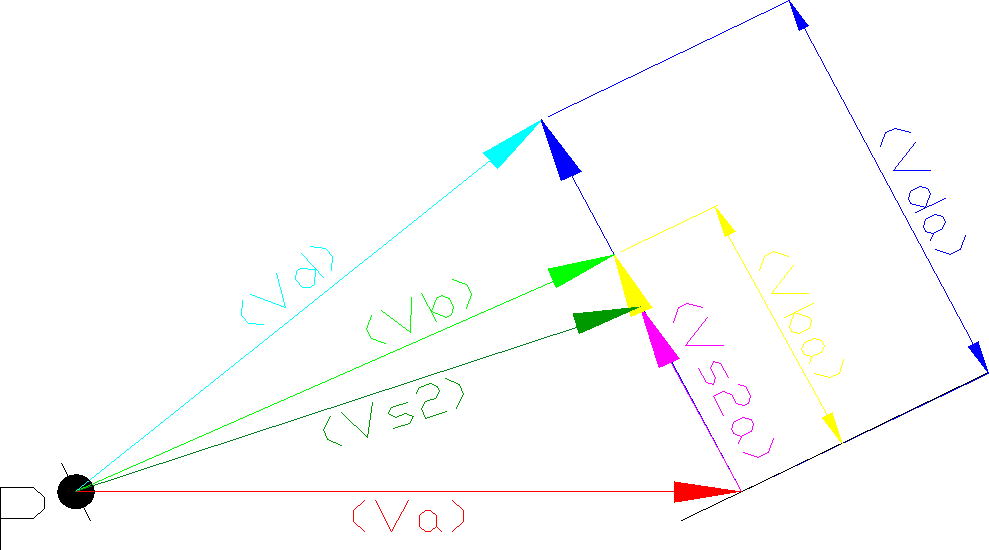
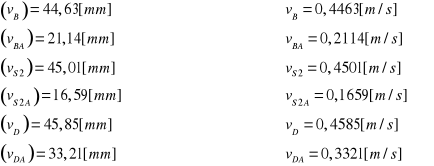
Grafoanalityczna metoda wzynaczania przyspieszeń mechanizmu.
Przyspieszenie członu napędzającego wynosi:
![]()
Wyznaczając przyspieszenie punktu B możemy zapisać równania:
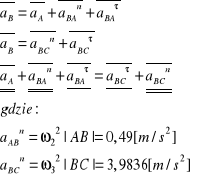

Przyspieszenie kątowe:
![]()
![]()
![]()
Wyznaczenie przyspieszenia pkt.D
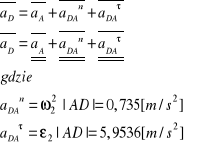
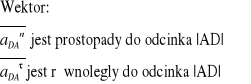
Wyznaczenie przyspieszenia pkt. środka masy S2
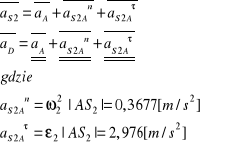
Przyjęcie podziałki rysunkowej dla planu przyśpieszeń:
![]()
Na podstawie powyższych obliczeń można utworzyć plan przyspieszeń:

Model mechanizmu w programie SAM:
Wykresy prędkości dla poszczególnych punktów w programie SAM
Wykresy przyspieszeń dla poszczególnych punktów w programie SAM
Metoda analityczna.
Dane: φ2 φ3
- φSA(t)=0
- φ0(t)=180
- l0(t)= 0,15[m]
- l2(t)=0,1[m]
- l3(t)=0,05[m]
położenie początkowe: sA(t)=0,0398[m]
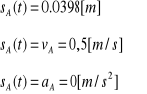
Mechanizm opisujemy wielobokiem wektorowym:
![]()
Po zrzutowaniu na osie układu:
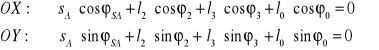
Uwzględniając:
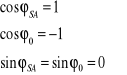
Otrzymujemy:
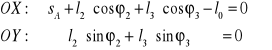
Oznaczając ![]()
, a następnie podnosząc obie strony do kwadratu i dodając stronami mamy:
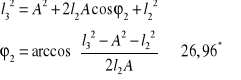
Nast. z równania OY wyznaczamy:
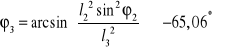
Analityczne wyznaczanie prędkości mechanizmu.
Aby wyznaczyć analitycznie prędkości kątowe mechanizmu, należy zróżniczkować równania OX i OY po czasie. Otrzymujemy:
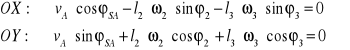
W celu wyznaczenia prędkości ![]()
obracamy układ współrzędnych o kąt φ3 :
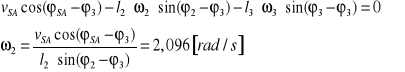
W celu obliczenia ![]()
obracamy układ współrzędnych kąt φ2 :
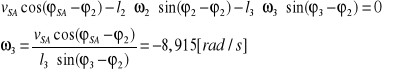
Analityczne wyznaczanie przyspieszeń mechanizmu.
Obliczamy drugą pochodną po przemieszczeniu:
![]()
Obracając układ współrzędnych o kąt ![]()
mamy:
![]()
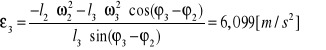
Obracając układ współrzędnych o kąt ![]()
mamy:
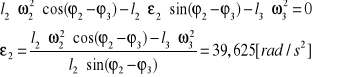
Wykresy prędkości katowych oraz przyspieszen w programie SAM
Dla czlonu drugiego
Dla czlonu trzeciego
|
metoda grafoanalityczna |
metoda analityczna |
Wyniki w programie SAM |
|
Prędkości [m/s] |
||||
vA |
0,5 |
0,5 |
0,5 |
|
vB |
0,446 |
- |
0,446 |
|
vD |
0,459 |
- |
0,455 |
|
vS2
|
0,449 |
- |
0,451 |
|
Prędkości [rad/s]
|
||||
ω2 |
2,214 |
2,109 |
2,117 |
|
ω3 |
8,926 |
-8,917 |
-8,916 |
|
Przyspieszenia [m/s2]
|
||||
aA |
0 |
0 |
0 |
|
aB |
3,964 |
- |
3,987 |
|
aD |
5,999 |
- |
5,981 |
|
aS2 |
2,995 |
- |
2,991
|
|
Przyspieszenia [rad/s2]
|
||||
ε2 |
39,691 |
39,625 |
-39,621 |
|
ε3 |
6,964 |
6,099 |
6,256 |
|
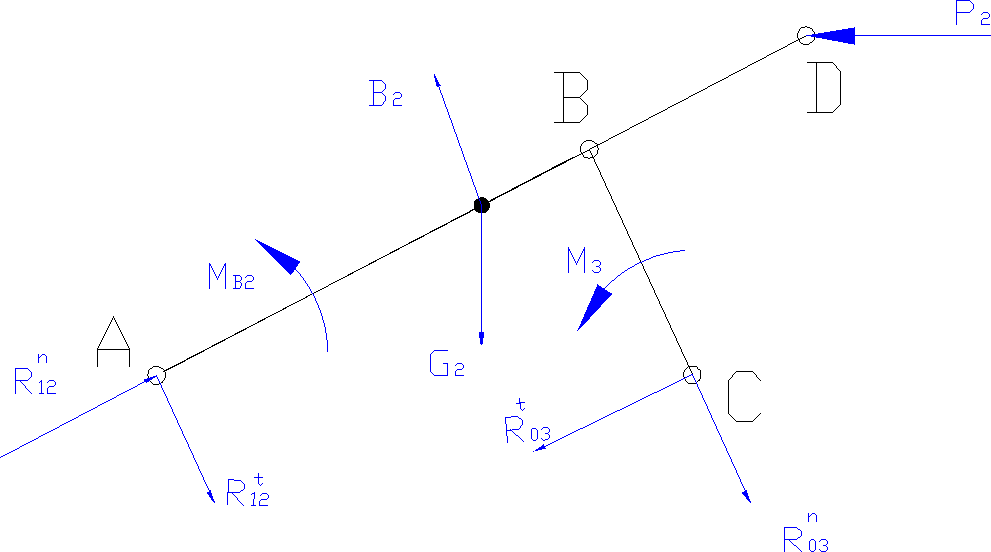
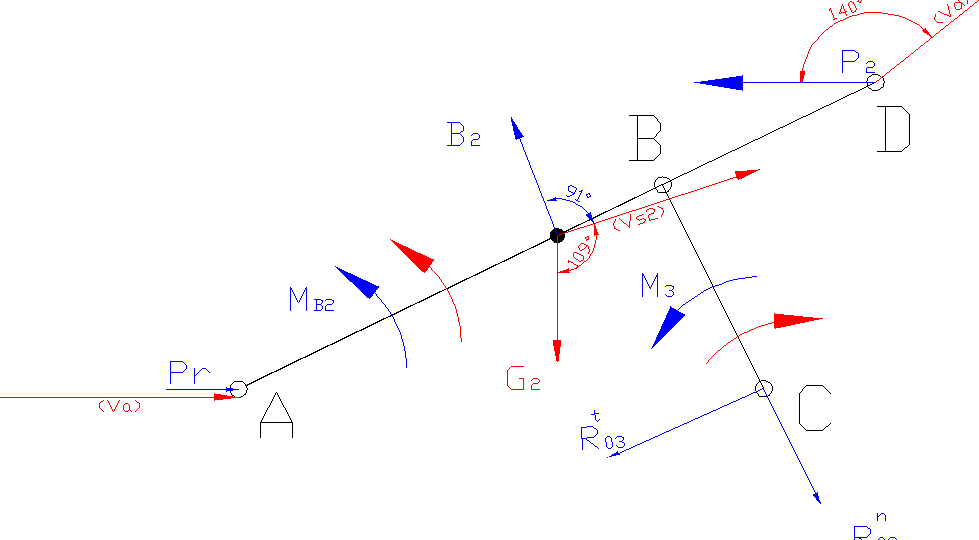
Analiza kinetostatyczna mechanizmu.
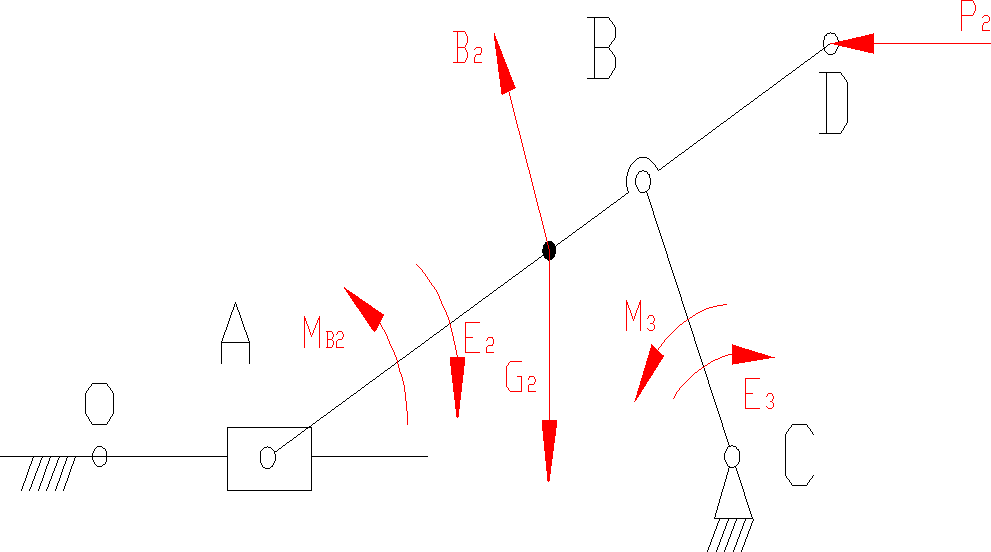
Na powyższym schemacie zaznaczono wszystkie obciążenia jakim poddany jest mechanizm. Siła B2 jest siłą bezwładności, której kierunek jest taki sam jak kierunek przyspieszenia aS2, a zwrot przeciwny do tego przyspieszenia. Przyspieszenie kątowe ε2 jest przeciwne do kierunku prędkości obrotowej; przyspieszenie ε3 jest zgodne z kierunkiem obrotu członu 3.
Dane:
P2=5[N]
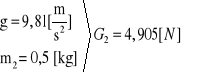
M3=0,5Nm
Moment bezwładności wzgl. punktu S2 na podstawie wzoru:
![]()
wyznaczenie sił bezwładności B2, momentu od siły bezwładności oraz siły przyciągania G2:
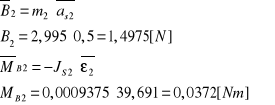
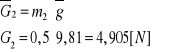
c) uwolnienie układu od więzów:
d) obliczenia sił
Po rozpisaniu sił dla członów 2 i 3 oraz dodaniu stronami powstałych równań otrzymujemy:
![]()
Równanie momentów dla członu 3 względem pkt B:
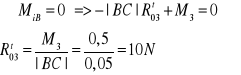
Równanie momentów dla członu 2 względem pkt B
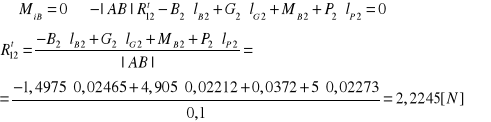
Otrzymujemy:
![]()
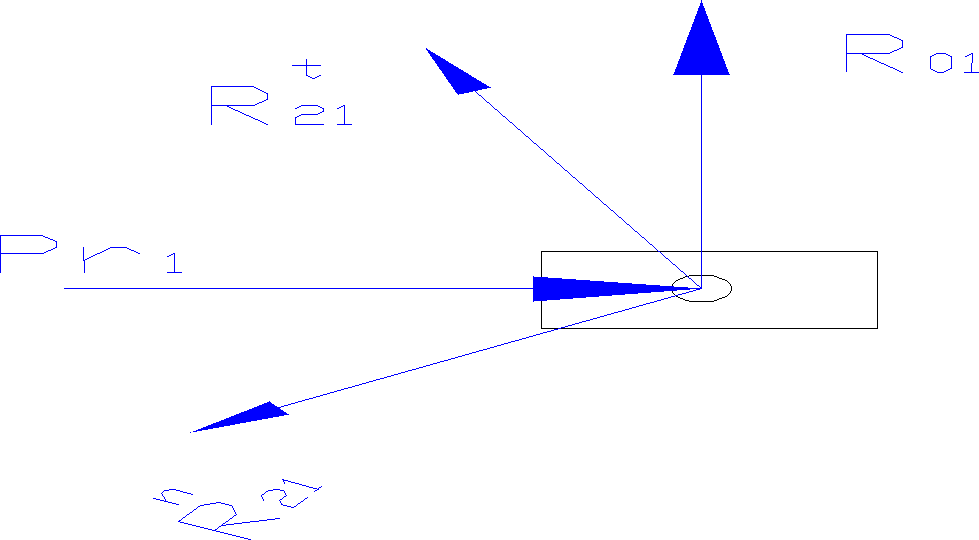
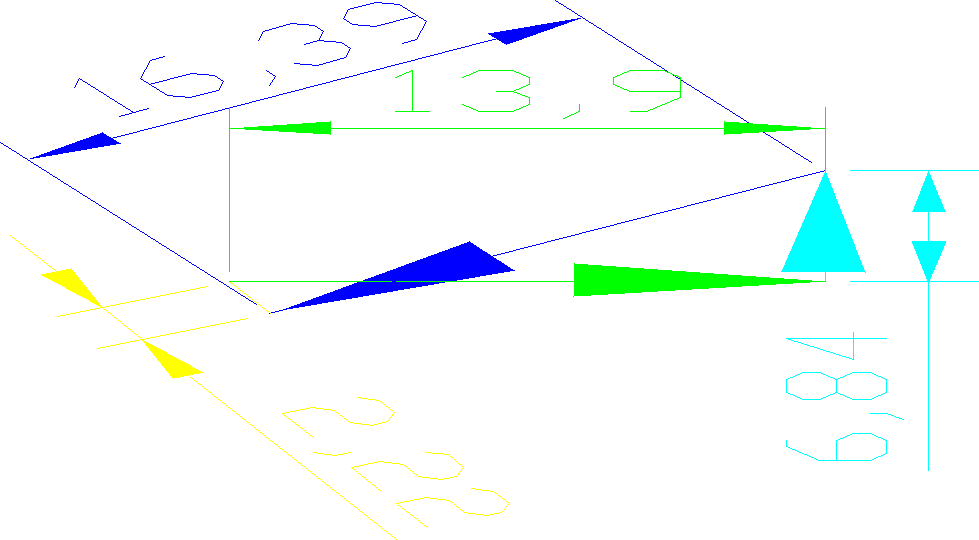
Przy pomocy programu AutoCAD można wykreślić plan sił działających na człony 2 i 3:
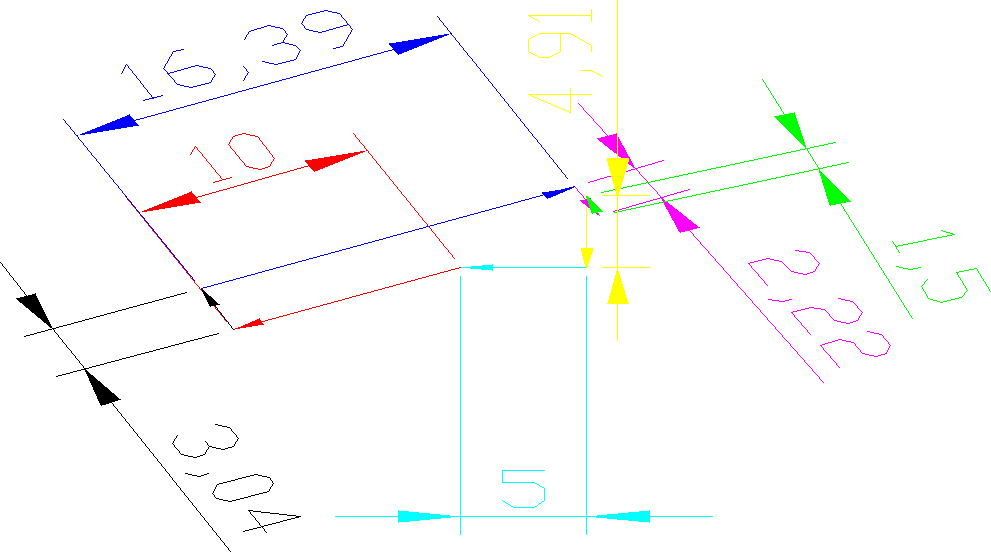
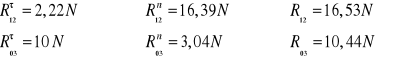
Człon napędzający:
|
|
Siła równoważąca: Pr=13,9[N]
Reakcji podłoża: R01=6,29[N]
Wyniki analizy kinestostatycznej wg programu SAM:
Metoda mocy chwilowych.
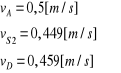
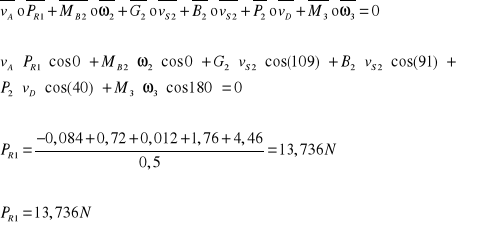
Siła równoważąca:
![]()
Podsumowanie analizy kinetostatycznej.
Rodzaj metody |
Metoda wykreślna |
Metoda mocy chwilowych |
Analiza kinetostatyczna w SAM-ie |
PR1 |
13,9 |
13,736 |
13,76 |
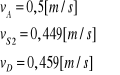
![]()
Wyszukiwarka