 | Pobierz cały dokument tmm.projekt.1b.projekty.teoria.maszyn.i.doc Rozmiar 484 KB |
Teoria Maszyn i Mechanizmów
Analiza Mechanizmu:
Krzysztof Batko
Gr. 16A
Rok akad. 2007/2008
Wymiary mechanizmu:
|AB|=0,1[m]
|BC|=0,05[m]
|OC|=0,15[m]
|BD|=0,05 [m]
Dane:
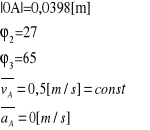
Grafoanalityczne wyznaczanie prędkości mechanizmu.
Zgodnie z przyjętą prędkością członu napędzającego, prędkość ![]()
=0,5[m/s].
Aby wyznaczyć prędkość punktu B należy zapisać równanie:
![]()
.
Człon 2 porusza się ruchem złożonym więc ![]()
to prędkość unoszenia, a ![]()
to prędkość ruchu względnego (ruch obrotowy wokół punktu A). Podwójne podkreślenie wektora oznacza, że znamy kierunek i wartość wektora; pojedyncze oznacza, że znamy jedynie kierunek wektora. Wektor ![]()
jest równoległy do |OA|, a ![]()
jest prostopadły do członu 2.
Dla punktu D możemy zapisać:
![]()
![]()
![]()
![]()
Wektor prędkości ![]()
jest prostopadły do |DA|
Wyznaczanie prędkości środka masy
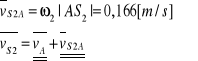
Podziałka rysunkowa dla planu prędkości:![]()
.
Na podstawie powyższych obliczeń można utworzyć plan prędkości (w programie AutoCAD):
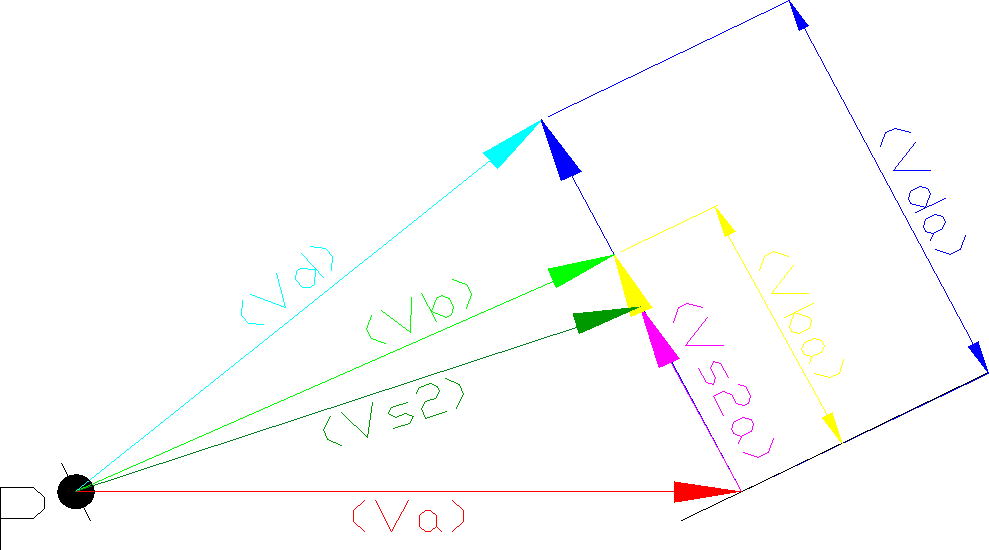
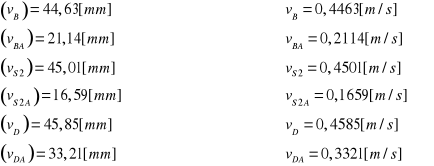
Grafoanalityczna metoda wzynaczania przyspieszeń mechanizmu.
Przyspieszenie członu napędzającego wynosi:
![]()
Wyznaczając przyspieszenie punktu B możemy zapisać równania:
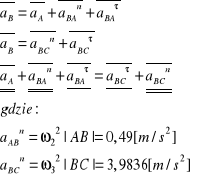

Przyspieszenie kątowe:
![]()
![]()
![]()
Wyznaczenie przyspieszenia pkt.D
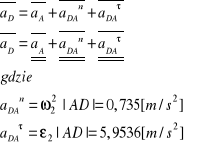
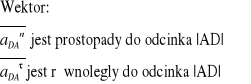
Wyznaczenie przyspieszenia pkt. środka masy S2
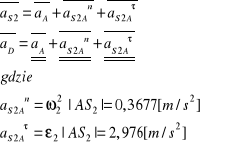
Przyjęcie podziałki rysunkowej dla planu przyśpieszeń:
![]()
Na podstawie powyższych obliczeń można utworzyć plan przyspieszeń:

Model mechanizmu w programie SAM:
Wykresy prędkości dla poszczególnych punktów w programie SAM
Wykresy przyspieszeń dla poszczególnych punktów w programie SAM
Metoda analityczna.
Dane: φ2 φ3
- φSA(t)=0
- φ0(t)=180
- l0(t)= 0,15[m]
- l2(t)=0,1[m]
- l3(t)=0,05[m]
położenie początkowe: sA(t)=0,0398[m]
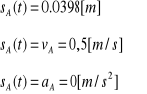
 | Pobierz cały dokument tmm.projekt.1b.projekty.teoria.maszyn.i.doc rozmiar 484 KB |