Imię i nazwisko
|
Ćwiczenie nr 19
Wyznaczanie współczynnika załamania światła metodą interferometru |
||
Kierunek i rok
Fizyka Mag. Uzup. I |
Ocena z kolokwium
|
Ocena ze sprawozdania
|
Ocena końcowa |
Prowadzący ćwiczenia
|
|
|
|
I CZĘŚĆ TEORETYCZNA
1.Oddziaływanie światła z materią.
Fala elektromagnetyczna, a więc i światło mogą rozchodzić się nie tylko w próżnia ale również w ośrodkach materialnych. Oddziaływanie światła (rozumianego jako strumień fotonów) z materią opisujemy przy pomocy następujących procesów:
emisji spontanicznej, w wyniku której foton emitowany jest samorzutnie przez wzbudzony atom,
emisji wymuszonej, w wyniku której foton oddziałujący ze wzbudzonym atomem wymusza emisję identycznego fotonu przez ten atom,
absorpcji, w wyniku której foton zostaje pochłonięty przez atom, a ten przechodzi w stan wzbudzony.
Emisja spontaniczna zachodzi, gdy elektrony znajdujące się na poziomach wzbudzonych w sposób spontaniczny wracają na niższe poziomy energetyczne, emitując przy tym fotony.
Emisja wymuszona zachodzi wtedy, gdy atom wzbudzony zderza się z fotonem o takiej częstotliwości, ze jego energia kwantu jest równa różnicy energii poziomów między stanem wzbudzonym a podstawowym. Foton uderzający nie ulega pochłonięciu, ale przyspiesza przejście atomu ze stanu wzbudzonego do podstawowego i dlatego z atomu wylatują w tym samym kierunku dwa spójne , to znaczy zgodne w fazie fotony o tej samej energii i częstotliwości.
Aby światło było absorbowane przez materię, energia fotonów musi odpowiadać różnicy energii poziomów energetycznych w atomach lub cząsteczkach, z którymi oddziałuje (energia fotonów jest bezpośrednio związana z długością fali światła czyli z jego barwą ). Wykorzystuje się to do identyfikacji nieznanych substancji, poprzez badanie absorpcji światła o różnych długościach fali w próbkach tych substancji. Jest to tak zwana absorpcyjna analiza spektroskopowa.
2. Interferencji i dyfrakcja
Interferencją fal nazywamy zjawisko nakładania się fal, w których zachodzi stabilne w czasie ich wzajemne wzmocnienie w jednych punktach przestrzeni, oraz osłabienie w zależności od stosunków fazowych fal.
Interferować mogą tylko fale spójne, dla których odpowiadające im drgania zachodzą wzdłuż tego samego lub podobnych kierunków.
Jeżeli odległość punktów w których fale są wytwarzane, wynosi Δx = λ/2, to w wyniku ich nałożenia nastąpi wygaszenie fali. Ogólnie możemy to zapisać wzorem
Δx = (2n+1) λ/2
n = 0,1,2,3,...
n - rząd widma
W przypadku, gdyby źródła fal były odległe od siebie o Δx = λ, zaobserwowalibyśmy wzmocnienie. Zapisujemy to ogólnym wzorem
Δx = nλ,
n = 0,1,2,3,...
Dyfrakcja światła polega na odchyleniu kierunku rozchodzenia się światła od pierwotnego kierunku, kiedy przechodzi ono przez niewielkie szczeliny, otwory lub natrafia na przeszkody.
Zjawisko dyfrakcji i interferencji fali
3. Równanie Clausiusa-Mossattiego
Równanie Clausiusa-Mossattiego opisuje zależność przenikalności dielektrycznej ε niepolarnego dielektryku od polaryzowalności α jego molekuł, atomów lub jonów i ich liczby N w jednostce objętości.
Polaryzowalność na mol wyrażam wzorem:
![]()
M - masa drobinowa
NA- liczba Avogadro
Wektor polaryzacji jest związany z polaryzowalnością równaniem:
![]()
N - polaryzowalność na jednostkę objętości
Z czego otrzymujemy:
![]()
lub:
![]()
Na podstawie powyższych wzorów otrzymujemy RÓWNANIE CLAUSIUSA-MOSSATTIEGO
![]()
Prawą stronę równania nazywamy refrakcją molową i oznaczamy R.
Z równiania Clausiusa-Mossattiego wynika, że refrakcja molarna jest wielkością stałą z pominięciem oddziaływania otoczenia na drobiny dielektryka.
4. Refrakcja
Refrakcja fali to zjawisko zmiany kierunku rozchodzenia się fali na granicy dwóch ośrodków, w których dana fala rozchodzi się z różnymi prędkościami. Kierunki rozchodzenia się fali załamanej i padającej zawarte są w jednej płaszczyźnie, spełnione jest także prawo Snelliusa.
Prawo Snelliusa - prawo optyki geometrycznej opisujące zjawisko załamania światła. Brzmi ono następująco: stosunek sinusa kąta padania do sinusa kąta załamania jest dla dwóch danych ośrodków wielkością stałą, równą stosunkowi szybkości światła w tych dwóch ośrodkach i nazywa się współczynnikiem załamania ośrodka drugiego względem pierwszego
n = sin α / sin β = v1 / v2
gdzie: n - współczynnik względny załamania,
α - kąt padania,
β - kąt załamania,
v1 - prędkość fali w ośrodku I,
v2 - prędkość fali w ośrodku II.
Jednym z celów ćwiczenia jest wykazanie, że refrakcja właściwa opisana poniższym wzorem jest wielkością stałą
![]()
5. Zasada działania i rodzaje interferometru
Interferomerty to przyrządy, w których wykorzystano zjawisko interferencji fal. W zależności od rodzaju fal dzieli się je na interferometry akustyczne i interferometry elektromagnetyczne. Interferometry stosuje się do pomiaru długości fal linii widmowych i badania ich struktury, do pomiaru współczynnika załamania ośrodków, do bezwzględnego i względnego pomiaru długości, do pomiaru rozmiarów kątowych gwiazd itd.
Zasada działania interferometru. Wiązka świetlna zostaje za pomocą pewnego urządzenia rozdzielona na dwie lub więcej wiązek spójnych, które po przebyciu różnych dróg optycznych zostają ponownie zebrane i ulegają interferencji. Interferometry wielowiązkowe stosowane są głównie jako spektroskopy interferencyjne o wysokiej zdolności rozdzielczej. Interferometry dwuwiązkowe są w większości przyrządami technicznymi. Typowymi interferometrami są interferometry Fabry'ego - Perota, Jamina, Macha - Zehndera, Michelsona, Rayleigha, Twymana - Greena.
6. Interferometr laboratoryjny LI - 3
Interferometr Rayleigha, refraktometr interferencyjny, rodzaj interferometru optycznego służący do bardzo precyzyjnego pomiaru różnicy współczynnika załamania światła dwóch ośrodków.Zbudowany jest ze źródła światła, obiektywu, diafragmy z dwiema szczelinami dyfrakcyjnymi (dyfrakcja fal), dwóch naczyń wypełnionych wzorcową i badaną substancją oraz lunetki z okularem cylindrycznym. Wychodząc ze źródła światła wiązka światła oświetla przez kondensator szczelinę i po przejściu przez obiektyw kolimatora biegnie równolegle. Ugięcie światła następuje na brzegach podwójnej przesłony, znajdującej się tuż za obiektywem. Dolna część wiązek światła przechodząca poniżej kuwety szklanej zostaje wprowadzona do lunety. Wiązki te wytwarzają w okularze stały układ prążków interferencyjnych. Górna wiązka światła przedostaje się do przez kuwety i płytki kompensacyjne również do lunety, dając w okularze górny, ruchomy układ prążków. Prążki interferencyjne obserwuje się przez lupę. Ponieważ soczewka powiększa obraz horyzontalnie, używa się światła o dużym natężeniu w celu uzyskania dobrej widoczności podziału linii poziomej.
Schemat interferometru LI-3
II. CZĘŚĆ PRAKTYCZNA
Cel ćwiczenia:
Celem ćwiczenia jest pomiar zależności współczynnika załamania światła od ciśnienia dla powietrza w danej temperaturze.
Przyrządy:
Interferometr Rayleigha typ LI-3 z oprzyrządowaniem, aparatura próżniowa, termometr.
Wykonanie ćwiczenia:
Odczytałam temperaturę z termometru.
Zamocowałam kuwetę czerwoną kropką w stronę okularu i podłączyłam do układu próżniowego.
Kurek 1 ustawiłam w pozycji Z (zapowietrzenie pompy), natomiast kurek 2 w pozycji pompującej obie komory. Kurek 3 zamknięty.
Włączyłam pompę rotacyjną, przekręciłam kurek 1 o 180 oC i pompowałam obie komory przez około 10 minut.
Ustawiłam ostrość prążków, odaretowałam śrubę mikrometryczną, wyzerowałam i zaaretowałam.
Kurek 2 ustawiłam w pozycji odpompowywania komory I i odcięcia komory II.
przy pomocy kurka 3 zmieniłam ciśnienie w komorze II i dopasowywałam obraz górnych prążków do dolnych. Różnicę dróg optycznych Δ odpowiadającą ustawionemu ciśnieniu odczytujemy na bębnie.
Czynności powtórzyłam dla innych kuwet.
Wyniki pomiarów:
Kuweta I
l =10[cm] =100[mm]
![]()
Tabela 1
Lp. |
Ciśnienie p [hPa] |
Różnica dróg optycznych Δ[mm] |
1 |
100 |
1,82 |
2 |
150 |
2,37 |
3 |
200 |
2,64 |
4 |
250 |
4,39 |
5 |
300 |
5,10 |
6 |
350 |
6,31 |
7 |
400 |
7,10 |
8 |
450 |
7,45 |
9 |
500 |
7,49 |
10 |
550 |
8,73 |
11 |
600 |
9,80 |
12 |
650 |
10,43 |
13 |
700 |
11,82 |
14 |
750 |
12,53 |
15 |
800 |
13,15 |
16 |
850 |
14,09 |
17 |
900 |
14,70 |
18 |
950 |
15,39 |
Kuweta II
l = 25[cm] = 250[mm]
![]()
Tabela2
Lp. |
Ciśnienie p [hPa] |
Różnica dróg optycznych Δ[mm] |
1 |
100 |
2,80 |
2 |
200 |
6,60 |
3 |
300 |
11,84 |
4 |
400 |
15,02 |
5 |
500 |
18,03 |
6 |
600 |
20,17 |
7 |
700 |
25,60 |
8 |
800 |
30,05 |
Kuweta III
l =50[cm] = 500[mm]
![]()
Tabela3
Lp. |
Ciśnienie p [hPa] |
Różnica dróg optycznych Δ[mm] |
1 |
50 |
2,54 |
2 |
100 |
5,19 |
3 |
150 |
10,20 |
4 |
200 |
12,65 |
5 |
250 |
18,09 |
6 |
300 |
21,97 |
7 |
350 |
27,35 |
8 |
400 |
31,03 |
Wyznaczanie współczynnika załamania światła dla poszczególnych ciśnień posługując się wzorem:
![]()
Kuweta I l = 10 [cm] =100 [mm]
Dla:
p = 100 [hPa]

n = 1,0182
p = 150 [hPa] n = 1,0237
p = 200 [hPa] n = 1,0264
p = 250 [hPa] n = 1,0439
p = 300 [hPa] n = 1,0510
p = 350 [hPa] n = 1,0631
p = 400 [hPa] n = 1,0710
p = 450 [hPa] n = 1,0745
p = 500 [hPa] n = 1,0779
p = 550 [hPa] n = 1,0873
p = 600 [hPa] n = 1,0980
p = 650 [hPa] n = 1,1043
p = 700 [hPa] n = 1,1182
p = 750 [hPa] n = 1,1253
p = 800 [hPa] n = 1,1315
p = 850 [hPa] n = 1,1409
p = 900 [hPa] n = 1,1470
p = 950 [hPa] n = 1,1539
Kuweta II l = 25 [cm] = 250 [mm]
Dla:
p = 100 [hPa] n = 1,0112
p = 200 [hPa] n = 1,0265
p = 300 [hPa] n = 1,0474
p = 400 [hPa] n = 1,0601
p = 500 [hPa] n = 1,0721
p = 600 [hPa] n = 1,0807
p = 700 [hPa] n = 1,1024
p = 800 [hPa] n = 1,1202
Kuweta III l = 50 [cm] = 500 [mm]
Dla:
p = 50 [hPa] n = 1,0051
p = 100 [hPa] n = 1,0104
p = 150 [hPa] n = 1,0204
p = 200 [hPa] n = 1,0253
p = 250 [hPa] n = 1,0362
p = 300 [hPa] n = 1,0439
p = 350 [hPa] n = 1,0547
p = 400 [hPa] n = 1,0621
Wykreślenie zależności współczynnika załamania światła od ciśnienia dla poszczególnych długości kuwet n = f(p).
Obliczanie gęstości powietrza dla poszczególnych ciśnień za pomocą wzoru:
![]()
![]()
Kuweta I ![]()
Dla:
p = 100 [hPa]
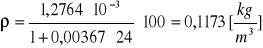
p = 150 [hPa]
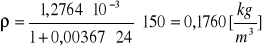
p = 200 [hPa]
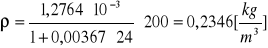
p = 250 [hPa]
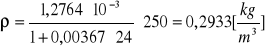
p = 300 [hPa]
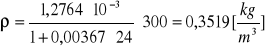
p = 350 [hPa]
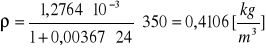
p = 400 [hPa]
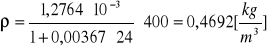
p = 450[hPa]
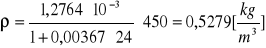
p = 500 [hPa]
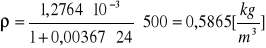
p = 550 [hPa]
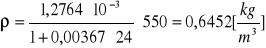
p = 600 [hPa]
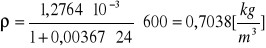
p = 650 [hPa]
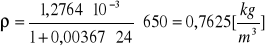
p = 700 [hPa]
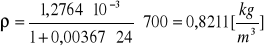
p = 750 [hPa]
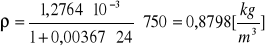
p = 800 [hPa]
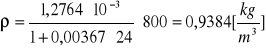
p = 850 [hPa]
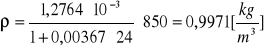
p = 900 [hPa]
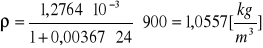
p = 950 [hPa]
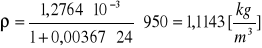
Kuweta II ![]()
Dla:
p = 100[hPa]
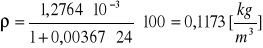
p = 200 [hPa]
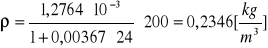
p = 300 [hPa]
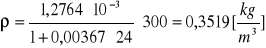
p = 400 [hPa]
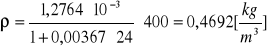
p = 500 [hPa]
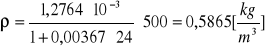
p = 600 [hPa]
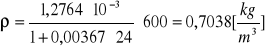
p = 700 [hPa]
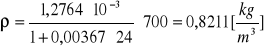
p = 800 [hPa]
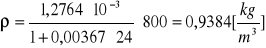
Kuweta III ![]()
Dla:
p = 50 [hPa]
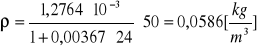
p = 100 [hPa]
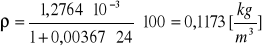
p = 150 [hPa]
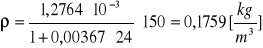
p = 200 [hPa]
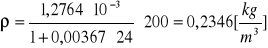
p = 250 [hPa]
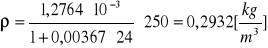
p = 300 [hPa]
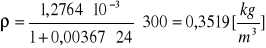
p = 350 [hPa]
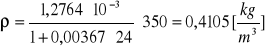
p = 400 [hPa]
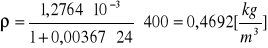
Obliczanie wartości refrakcji używając wzoru:
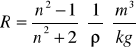
Kuweta I
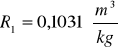
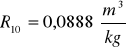
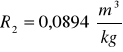
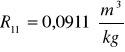
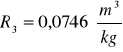
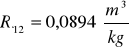
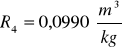
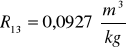
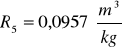
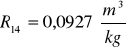
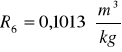
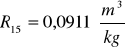
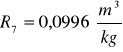
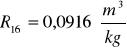
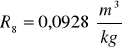
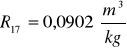
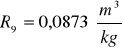
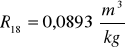
Kuweta II
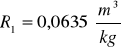
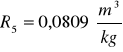
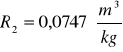
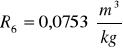
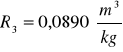
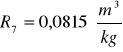
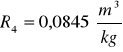
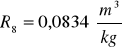
Kuweta III
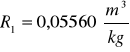
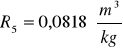
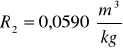
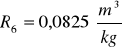
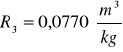
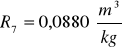
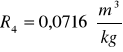
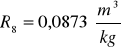
Obliczam wartość średnia z refrakcji molarnej
dla kuwety I
![]()
dla kuwety II
![]()
dla kuwety III
![]()
Dokładność interferometru jest zależna od długości kuwety. Im większa jest długość kuwety, tym dokładniejszy jest pomiar. Z drugiej strony większa długość kuwety zmniejsza zakres pomiaru
Niepewność współczynnika załamania światła wynosi tyle co niepewność śruby mikrometrycznej czyli.
![]()
Niepewność gęstości powietrza dla poszczególnych dla poszczególnych ciśnień wynosi:
![]()
Może być ona obarczona niepewnością temperatury, którą odczytuję z termometru [T] = 1 oC
III. WNIOSKI
Celem ćwiczenia było wykonanie pomiaru zależności współczynnika załamania światła od ciśnienia w danej temperaturze.
Po wykonaniu pomiarów obliczono ze stosownych wzorów współczynniki załamania światła, gęstość powietrza oraz refrakcje właściwą.
Otrzymane wyniki są do siebie zbliżone, należy powiedzieć, iż pojawiły się błędy które mają wpływ na otrzymane wyniki. W trakcie wykonywania ćwiczenia nie udało się rozpocząć pomiarów od ciśnienia 0 hPa, wpływ na otrzymane wyniki ma na pewno zaokrąglenie wyników i użycie wzorów. Niestety nie udało się wykonać pomiarów w idealnych warunkach ze względu na nieszczelność aparatury.
Wyszukiwarka