2. Pociąg o długości L₁ = 100 m jedzie z prędkością v₁ = 45 km/godz. Po sąsiednim torze jedzie z prędkością v₂ = 81 km/godz. pociąg o długości L₂ = 75 m. Obliczyć:

a) czas mijania się pociągów, gdy ich prędkości mają przeciwne zwroty,

b) czas wyprzedzania, gdy zwroty prędkości są zgodne.

R. Pociągi zaznaczamy jako grube kolorowe strzałki. Wzdłuż torów prowadzimy oś liczbową OX. Drogę przebywaną przez wybrany punkt pociągu opisujemy przez zmianę współrzędnej tego punktu, czyli s_x = Δx = x_końc - x_pocz. Droga może być tutaj ujemna, gdy x_końc < x_pocz. Wektory prędkości mają w tym zadaniu tylko współrzędne x-owe, czyli v_x. Wzór s = v·t przybiera postać s_x = v_x·t, więc x_końc - x_pocz = v_x·t.

a) mijanie się pociągów;

1) Początek mijania, przednie obrysy pociągów znajdują się w punktach o współrzędnej x = 0.

Tylny obrys pierwszego pociągu ma współrzędną x_1pocz = -L₁, a drugiego pociągu - współrzędną x_2pocz = L₂. Ponieważ pierwszy pociąg jedzie zgodnie ze zwrotem osi OX, to x-owa współrzędna jego prędkości wynosi v_1x = v₁. Drugi pociąg jedzie przeciwnie do zwrotu osi OX, więc x-owa współrzędna jego prędkości wynosi v_2x = -v₂.

2) Koniec mijania, tylne obrysy pociągów mają tę samą współrzędną x_końc.

Oznaczamy współrzędną tylnego obrysu pierwszego pociągu przez x_1t. Po upływie czasu t od początku mijania, drogę tego obrysu można zapisać następująco x_1t - x_1pocz = v_1x·t, czyli

x_1t - (-L₁) = v₁·t, a stąd x_1t = v₁·t - L₁.

Podobnie współrzędną tylnego obrysu drugiego pociągu oznaczamy przez x_2t. Po czasie t od początku mijania, drogę tego obrysu można zapisać w postaci x_2t - x_2pocz = v_2x·t, czyli

x_2t - L₂ = -v₂·t, a stąd x_2t = -v₂·t + L₂.

Mijanie kończy się po czasie t_m i wtedy x_1t = x_2t = x_końc, co daje równanie

v₁·t_m - L₁= -v₂·t_m + L₂.

Czas mijania wynosi zatem

?

b) wyprzedzanie (pociągu pierwszego przez drugi);

1) Początek wyprzedzania, tylny obrys pierwszego pociągu i przedni obrys drugiego pociągu znajdują się w punktach o współrzędnej x = 0.

Przedni obrys pierwszego pociągu ma współrzędną x_1pocz = L₁, a tylny obrys drugiego pociągu współrzędną x_2pocz = -L₂. Oba pociągi jadą zgodnie ze zwrotem osi OX, więc x-owe współrzędne ich prędkości wynoszą v_1x = v₁, v_2x = v₂.

2) Koniec wyprzedzania, teraz przedni obrys pierwszego pociągu i tylny obrys drugiego pociągu mają tę samą współrzędną x_końc.

Oznaczamy współrzędną przedniego obrysu pierwszego pociągu przez x_1p. Po upływie czasu t od początku wyprzedzania, drogę tego obrysu można zapisać następująco x_1p - x_1pocz = v_1x·t, czyli

x_1p - L₁ = v₁·t, a stąd x_1p = v₁·t + L₁.

Tak, jak dla mijania, tylny obrys drugiego pociągu ma współrzędną x_2t. Po czasie t od początku wyprzedzania, drogę tego obrysu można zapisać w postaci x_2t - x_2pocz = v_2x·t, czyli

x_2t - (-L₂) = v₂·t, a stąd x_2t = v₂·t - L₂.

Wyprzedzanie kończy się po czasie t_w i wtedy x_1p = x_2t = x_końc, co teraz daje równanie

v₁·t_w + L₁= v₂·t_w - L₂.

Otrzymujemy czas wyprzedzania

?

Uwaga. Długości pociągów podano w metrach, a ich prędkości w km/godz. Przed obliczeniami należy więc ujednolicić jednostki. Zalecenie używania układu SI, ale też zdrowy rozsądek, powinny skłonić do użycia metrów i sekund (nikt chyba nie spodziewa się, że czasy mijania czy wyprzedzania będą porównywalne z godziną!)

5. Motorówka osiąga prędkość v_m = 3 m/s płynąc po stojącej wodzie. Kierowca łodzi chce przepłynąć rzekę o szerokości d = 200 m, prostopadle do brzegów. Nurt ma względem brzegów prędkość v₀ = 0,5 m/s. Pod jakim kątem względem brzegów należy utrzymywać kadłub łodzi? Jak długo potrwa przepłynięcie rzeki? Jaki byłby kątowy znos łodzi, gdyby kadłub ustawiono prostopadle do brzegów? Jak daleko od zaplanowanego miejsca motorówka przybiłaby do brzegu? Jak długo wtedy płynęłaby łódź do celu, gdyby kierowca zawrócił i płynął dalej wzdłuż brzegu?

R. Nurt rzeki zniósłby łódź do punktu P'. Wioślarz dopłynąłby do punktu P' z prędkością wypadkową
. Jej wartość liczymy z tw. Pitagorasa (v'_wyp)² = (v_m)² + (v₀)², czyli

.

Płynąłby po drodze s, liczonej także z tw. Pitagorasa s² = d ² + z², gdzie znos
(liczony na zajęciach). Mamy stąd

.

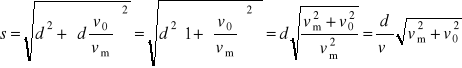
Czas t' płynięcia do P' obliczymy ze wzoru s = v'_wyp·t' , a to daje

(*)

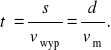
Czas t' jest taki sam, jaki zabrałoby przepłynięcie szerokości rzeki d, prostopadle do brzegów z prędkością v_m. Wynika to z zasady niezależności ruchów. Jeżeli wektor prędkości łodzi względem wody
jest prostopadły do brzegów, to przepłynięcie przez rzekę trwa tyle samo, niezależnie od tego, czy zachodzi dodatkowy ruch związany ze znoszeniem łodzi przez nurt. Następnie wioślarz zawraca z punktu P' do punktu P, płynie więc pod prąd po drodze z. Jego prędkość jest różnicą prędkości względem wody i prędkości samej wody, czyli jest to wartość v_pp = v_m - v₀, podobnie jak w zadaniu 3. Czas t" przepłynięcia tego odcinka liczymy ze wzoru z = v_pp·t", zatem

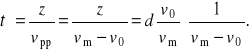
Całkowity czas dopłynięcia do punktu docelowego P wynosi t_c = t'+ t", czyli

= ?

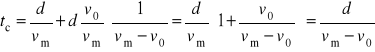
Jest to wyidealizowana rzeka, w której woda płynie z taką samą prędkością v₀ na całej szerokości d.

13. Za pomocą linki można podnosić ze stałym przyspieszeniem ciała o masie nie większej od m₁ = 4 kg. Ta sama linka umożliwia opuszczanie z tym samym przyspieszeniem ciał o masie nie większej od m₂ = 5 kg. Jakie największe naprężenie wytrzymuje linka? Jaką największą masę można podnosić na tej lince ruchem jednostajnym?

R. W czasie ruchu ciała linka jest rozciągana siłą naprężenia N. Siła ta działa na ciało pionowo w górę. Pionowo w dół działa siła ciężkości Q = mg, zatem dla podnoszenia ciała o masie m z przyspieszeniem a, z II zasady dynamiki wynika równanie m·a = N - m·g. Można je zapisać w formie N = m(g + a). Dla danego przyspieszenia naprężenie rośnie ze zwiększaniem masy. Dla masy m = m₁ naprężenie przyjmuje wartość krytyczną N_k, zatem

m₁·a = N_k - m₁·g. (1)

W przypadku opuszczania ciała mamy równanie m·a = m·g - N, skąd N = m(g - a). Dla masy m = m₂ naprężenie N = N_k, więc

m₂·a = m₂·g - N_k. (2)

Z układu równań (1) i (2) dostajemy
= ?, ponadto można wyznaczyć a = ?

Przy podnoszeniu ruchem jednostajnym mamy a = 0 i dla pewnej masy m₀ równanie (1) przybiera kształt 0 = N_k - m₀·g, z którego wyznaczamy m₀ = N_k /g = ?

14. Człowiek o masie m₁ = 60 kg stoi w windzie na wadze sprężynowej. Gdy winda jechała z pewnym przyspieszeniem w dół waga wskazywała ciężar P₁ = 570 N. Następnie na wadze zamiast pierwszego człowieka stanął drugi a winda ruszyła w górę z przyspieszeniem większym o Δa = 0,15 m/s² niż w czasie jazdy w dół. Waga wskazywała wtedy P₂ = 760 N. Jaką masę ma drugi człowiek?

R. Wskazanie wagi P jest równe naciskowi N, który wywiera umieszczony na niej obiekt. Waga „odpowiada” na ten nacisk siłą reakcji R, a z III zasady dynamiki wynika, że R = N = P. Dla uproszczenia, człowieka reprezentuje szary prostokąt. Na człowieka działają dwie pionowe siły: w dół siła ciężkości Q = mg i w górę siła reakcji R.

a) jazda w dół człowieka o masie m₁

z II zasady dynamiki m₁·a = Q₁ - R₁,

przy czym Q₁ = m₁·g, R₁ = N₁ = P₁.

zatem m₁·a = m_1·g - P₁, (*)

b) jazda w górę człowieka o masie m₂

z II zasady dynamiki m₂·a' =  R₂ - Q₂

ale a' = a + Δa, Q₂ = m₂·g, R₂ = N₂ = P₂.

zatem m₂·(a + Δa) = P₂ - m₂·g, (**)

Z (*) eliminujemy
, wstawiamy do (**) i dostajemy

 ?

15. Na poziomym podłożu stoją dwie skrzynki o masach m₁ = 12 kg i m₂ = 8 kg, związane poziomą linką, wytrzymującą naprężenie do N_k = 40 N. Współczynniki tarcia skrzynek o podłoże wynoszą odpowiednio μ₁ = 0,4 i μ₂ = 0,3. Jaką największą siłą, przyłożoną do masy m₁ poprzez poziomą linkę, można ciągnąć obie skrzynki? Jakie jest wówczas przyspieszenie tego układu? Jaka jest odpowiedź gdy siłę przyłożono do masy m₂?

R. Niech ruch zachodzi zgodnie ze zwrotem osi X. Wielkości, których wektory mają zwroty zgodne ze zwrotem osi X, przyjmujemy za dodatnie. Można założyć, że do masy m₁ przyłożono pewną umiarkowaną siłę F, która wywołuje naprężenie N w lince łączącej skrzynki. Od podłoża działają siły tarcia: na masę m₁ siła T₁, na masę m₂ siła T₂. Skrzynki wywierają na podłoże naciski normalne odpowiednio N₁ i N₂, którymi są ich ciężary, czyli N₁ = Q₁ = m₁·g, N₂ = Q₂ = m₂·g. Siły tarcia wyrażają się wobec tego wzorami: T₁ = μ₁·N₁ = μ₁·m₁·g, T₂ = μ₂·N₂ = μ₂·m₂·g. Dopóki linka łącząca skrzynki nie zrywa się, obie masy mają to samo przyspieszenie a, zatem z II zasady dynamiki mamy równania ruchu skrzynek

m₁·a = F - μ₁·m₁·g - N, m₂·a = N - μ₂·m₂·g. (*)

Stąd naprężenie
. Ale naprężenie nie może przekroczyć N_k, a to prowadzi do nierówności N ≤ N_k, która daje ograniczenie na siłę ciągnącą

111,77 N.

Przyspieszenie najszybciej liczy się dodając stronami równania (*) i wstawiając znalezione F_max. Dostajemy
2,057 m/s².

Ruch zachodzi gdy F ≥ (μ₁m₁ + μ₂m₂)g, czyli siła ciągnąca jest co najmniej równa sumie sił tarcia. Gdy siłę F przyłożyć do masy m₂, to z tyłu znajdzie się masa m₁, którą może ciągnąć naprężona linka zgodnie z równaniem m₁a = N - μ₁m₁g. Masa m₁ poruszy się gdy naprężenie będzie nie mniejsze niż siła tarcia siła, zatem dla N ≥ μ₁m₁g = 47,1 N. To jest jednak więcej niż naprężenie krytyczne N_k, czyli linka zerwie się przy próbie wprawienia układu w ruch.

16. Paleta o masie m₁ = 5 kg leży na poziomej podłodze. Współczynnik tarcia kinetycznego palety o podłogę wynosi μ₁ = 0,4. Na palecie leży paczka o masie m₂ = 1 kg. Współczynnik tarcia statycznego paczki o deskę równy jest μ₂ = 0,6. Jaką największą poziomą siłą można ciągnąć paletę aby paczka nie zsunęła się z niej?

R. Niech siła F ciągnie paletę, tak, że paczka nie zsuwa się. Od podłoża działa na paletę siła tarcia T₁, a od paczki siła tarcia T₂. Siły te, zgodnie z II zasadą dynamiki, nadają jej przyspieszenie a, więc

m₁·a = F - T₁ - T₂. (*)

Paleta z paczką działają na podłoże naciskiem normalnym, równym łącznemu ciężarowi, więc siła T₁ dana jest wzorem T₁ = μ₁·(m₁ + m₂)g. Tarcie między paletą a paczką jest statyczne. Ponieważ nacisk normalny paczki na podłoże jest równy ciężarowi paczki, to wartość siły T₂ ograniczona jest nierównością T₂ ≤ μ₂·m₂·g. Zgodnie z III zasadą dynamiki, paleta działa na paczkę siłą T_p = T₂. Siła ta nadaje także paczce przyspieszenie a, więc z II zasady dynamiki mamy równanie dla paczki

m₂·a = T₂.

Z powyższego równania mamy a = T₂/m₂. Wstawiamy to wyrażenie i wyrażenie na siłę T₁ do równania (*) i wyznaczamy siłę T₂

.

Uwzględniamy warunek T₂ ≤ μ₂·m₂·g i otrzymujemy ograniczenie na siłę ciągnącą

F  (μ₁ + μ₂)(m₁ + m₂)g = 58,9 N.

18. Równia jest nachylona pod kątem α = 25° względem poziomu. Klocek mający u podnóża równi prędkość v₀ = 5 m/s zaczyna płynnie wsuwać się na równię, a następnie zsuwa się z niej. Współczynnik tarcia klocka o równię wynosi μ = 0,4. Po jakim czasie od początku wsuwania klocek znajdzie się z powrotem u podstawy równi?

R. Ruch klocka po równi odbywa się pod działaniem siły ciężkości Q i siły tarcia kinetycznego T. Do opisu ruchu posługujemy się układem współrzędnych, którego oś X jest równoległa do zbocza równi, a oś Y - prostopadła do zbocza. Ciężar rozkładamy na składowe wzdłuż tych osi. Równię reprezentuje szary prostokątny trójkąt ABC. Kąt ACB jest równy α. Bok AB jest pionowy, a bok
BC poziomy. Składowa 
 jest więc równoległa do zbocza równi, a składowa
- prostopadła do tego zbocza. Ponieważ
|| AB, to kąt β jest równy kątowi BAC, czyli mamy β = 90° - α. Kąt pomiędzy
a
też jest równy β, więc
. Ale skoro β = 90° - α, to cosβ = sinα, stąd Q_x = Qcosβ = Qsinα. Ponadto
, więc kąt pomiędzy
a
jest równy α. Dlatego
, a stąd Q_y = Qcosα. Ciężar zapisujemy w postaci Q = mg, gdzie m jest masą klocka. Wobec tego Q_x = mgsinα oraz Q_y = mgcosα.

Ruch odbywa się równolegle do osi X. Składowa
pełni rolę nacisku normalnego
, czyli prostopadłego do podłoża. Siła tarcia dana jest więc wzorem T = μN_n = μmgcosα.

a) wsuwanie się klocka

Siły Q_x i T są zwrócone przeciwnie do ruchu klocka. Z II zasady dynamiki dostajemy równanie

m·a₁ = -Q_x - T = -mgsinα - μmgcosα.

Przyspieszenie klocka w czasie wsuwania wynosi zatem

a₁ = -g(sinα + μcosα),

a jego prędkość jest równa v = v₀ + a₁·t. Wsuwanie zakończy się po czasie t₁, gdy klocek zatrzyma się, czyli v₀ + a₁·t₁ = 0. Czas wsuwania się dany jest wyrażeniem t₁ = -v₀/a₁. Wstawiając to do wzoru na drogę s₁ = v₀·t₁ +a₁·t₁²/2, uzyskujemy

s = -v₀²/2a₁.

b) zsuwanie się klocka

Siła Q_x jest zwrócona zgodnie z ruchem, a siła T przeciwnie do ruchu klocka. Z II zasady dynamiki

m·a₂ = Q_x - T= mgsinα - μmgcosα.

W czasie zsuwania klocek ma więc przyspieszenie

a₂ = g(sinα - μcosα),

a jego drogę do podstawy można wyrazić wzorem s₂ = a₂·t₂²/2, gdzie t₂ jest czasem zsuwania się i wynosi t₂ =
. Z treści zadania wynika, że s₂ = s.

Uwzględniając wyrażenia na a₁, a₂ i s obliczamy czas powrotu klocka do podstawy równi

?

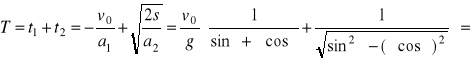
19. Pochylnia tworzy kąt α = 15° względem poziomu. Po pochylni zaczęto wciągać dwie skrzynie o masach m₁ = 6 kg i m₂ = 4 kg, połączone linką równoległą do zbocza pochylni. Siła ciągnąca o wartości P = 70 N była przyłożona do masy m₁ równolegle do zbocza pochylni. Współczynniki tarcia mas m₁ i m₂ o podłoże wynosiły odpowiednio μ₁ = 0,3 i μ₂ = 0,4. Jak długo trwało wciąganie skrzyń na wysokość h = 1,5 m? Jaką siłę należy przyłożyć do masy m₂, aby zsunąć skrzynie z tej wysokości w tym samym czasie? Jaka może być największa wartość siły ciągnącej jeżeli linka łącząca skrzynki wytrzymuje naprężenia do N_k = 40 N?

R. Dla przypomnienia na rysunku poniżej jest rozkład siły ciężkości Q = mg, ciała o masie m, znajdującego się na równi. Tak, jak podano w rozwiązaniu zadania 29. otrzymujemy wartości składowych: Q_x = Qsinα = mgsinα, Q_y = Qcosα = mgcosα.

a) wciąganie skrzyń

Zaznaczone są osie układu współrzędnych XY. Oś X-ów ma kierunek i zwrot zgodny z ruchem skrzyń. Oprócz składowych ciężarów skrzyń zaznaczono siłę ciągnącą P, siły tarcia kinetycznego skrzyń podłoże T₁ i T₂ oraz siłę naprężenia linki N.

Ruch skrzyni o masie m₁

Zgodnie kierunkiem ruchu działa siła ciągnąca P, a przeciwnie do kierunku ruchu: składowa Q_1x, siła tarcia T₁ i siła naprężenia N. Zapis równania II zasady dynamiki ma postać

m₁·a = P - Q_1x - T₁ - N.

Ruch skrzyni o masie m₂

Zgodnie kierunkiem ruchu działa siła naprężenia N, a przeciwnie do kierunku ruchu składowa Q_2x i siła tarcia T₂. Równanie II zasady dynamiki ma postać

m₂·a = N - Q_2x - T₂.

Składowe x-owe sił ciężkości są równe Q_1x = Q₁·sinα = m₁·gsinα, Q_2x = Q₂·sinα = m₂·gsinα. Naciski normalne skrzyń na podłoże wynoszą N_n1 = Q_1y, N_n2 = Q_2y, zatem siły tarcia są równe T₁ = μ₁·N_n1 = μ₁·m₁·gcosα, T₂ = μ₂·N_n2 = μ₂·m₂·gcosα. Równania ruchu obu mas przybierają więc formę układu równań

m₁·a = P - m₁·gsinα - μ₁·m₁·gcosα - N, (1)

m₂·a = N - m₂·gsinα - μ₂·m₂·gcosα. (2)

Dodając stronami równania dostajemy

a(m₁ + m₂) = P - gsinα(m₁+ m₂) - gcosα(μ₁·m₁ + μ₂·m₂)

Przyspieszenie układu mas wynosi

?

Przyspieszenie jest stałe a ponieważ skrzynie zaczęto ciągnąć, to miały prędkość początkową v₀ = 0. Droga skrzyń po czasie t od początku ciągnięcia wynosi
. Z rysunku widać, że
. Stąd czas wciągania skrzyń na wysokość h wynosi
?

b) zsuwanie skrzyń

Oś X-ów ma ten sam kierunek ale przeciwny niż poprzednio zwrot. Nieznana siła ciągnąca P' przyłożona jest do skrzyni m₂. Siła naprężenia ma inną wartość N'. Siły tarcia mają te same wartości ale przeciwne zwroty. Wartości i zwroty Q_1x, Q_2x, Q_1y, Q_2y pozostają bez zmian.

Ruch skrzyni o masie m₁

Zgodnie kierunkiem ruchu działa siła naprężenia N' i składowa Q_1x, a przeciwnie do kierunku ruchu siła tarcia T₁. Piszemy równanie II zasady dynamiki w postaci

m₁·a' = N' + Q_1x - T₁.

Ruch skrzyni o masie m₂

Zgodnie kierunkiem ruchu działa siła ciągnąca P' i składowa Q_2x, a przeciwnie do kierunku ruchu siła tarcia T₂ i siła naprężenia N'. Z II zasady dynamiki wynika równanie

m₂·a' = P' + Q_2x - T₂ - N'.

Układ równań ruchu ma teraz następującą formę

m₁·a' = N' + m₁·gsinα - μ₁·m₁·gcosα (1')

m₂·a' = P' + m₂·gsinα - μ₂·m₂·gcosα - N'. (2')

Przyspieszenie wyraża się teraz wzorem

.

Skrzynie zsuwają się z tej samej wysokości h, więc ich droga
będzie także taka sama, jak przy wciąganiu. Czas zsuwania ma być także ten sam, w takim razie ze wzoru
wynika, że „nowe” przyspieszenie a' musi być takie, jak „stare” przyspieszenie a. Przyrównujemy a' = a i po przekształceniach uzyskujemy wartość siły ciągnącej w dół

P' = P - 2(m₁ + m₂)·g·sinα = ?

Aby wyznaczyć największe wartości sił ciągnących w obu przypadkach wyliczamy z układów równań ruchu siły naprężenia linki i przyrównujemy je do wartości maksymalnej N_k.

a) wciąganie skrzyń

Z układu (1) i (2) uzyskujemy wartość siły naprężenia

.

Z powyższego wzoru widać, że gdy rośnie siła ciągnąca P, to rośnie też siła naprężenia N. Gdy zwiększymy siłę P do pewnej wartości P_max, to wartość N osiągnie N_k, czyli

.

Stąd największa wartość siły ciągnącej w górę wynosi

?

b) zsuwanie skrzyń

Podobnie z układu (1') i (2') dostajemy

.

W powyższej równości podstawiamy N' = N_k oraz P' = P'_max i po przekształceniach otrzymujemy największą wartość siły ciągnącej w dół

?

23. Wiaderko ze znajdującym się w nim kamykiem obraca się w płaszczyźnie pionowej ze stałą prędkością kątową. Promień okręgu zakreślanego przez kamyk równy jest r = 90 cm. Jaka jest najmniejsza liczba obrotów na minutę, przy której kamyk nie wypadnie z wiaderka?

R. Kamyk jest jasnoniebieski. Traktujemy go jak punkt materialny, w którym skupiona jest cała masa i przyłożone wszystkie siły. Siły te to ciężar Q = mg i siła reakcji R, pochodząca od dna wiaderka (brązowe). Wypadnięcie kamyka grozi tylko gdy znajduje się on na górnej części okręgu. Rysunek przedstawia sytuację gdy promień okręgu, przechodzący przez kamyk, tworzy z pionem kąt α. Siła dośrodkowa F_r jest tu sumą składowej ciężaru wzdłuż promienia, oznaczonej przez Q_r i siły reakcji R, czyli F_r = Q_r + R. Siły, które składają się na siłę dośrodkową i są zwrócone do środka okręgu, bierze się ze znakiem „+”. Siła Q_r ma taki zwrot na górnej części okręgu, a siła reakcji powinna mieć taki zwrot w każdym położeniu kamyka. Kamyk nie wypada z wiaderka, gdy wywiera na dno nacisk N. Istnienie nacisku pociąga za sobą istnienie reakcji na nacisk. Reakcja jest równa R = F_r - Q_r. Musi ona być nieujemna, tzn. być skierowana tak samo jak siła Q_r, czyli od dna do środka okręgu. Inaczej nie byłaby to reakcja dna, lecz siła „klejąca” kamyk do dna. A kleju tu nie ma. Składowa ciężaru wzdłuż promienia jest równa Q_r = Qcosα = mgcosα. Ogólny wzór na siłę dośrodkową ma postać

albo F_r = mω²r ponieważ v = ωr

m - masa kamyka, v - jego prędkość, ω - prędkość kątowa w ruchu po okręgu. Skoro R ≥ 0 w każdym położeniu, to F_r - Q_r ≥ 0, czyli mω²r - mgcosα ≥ 0, a zatem ω²r ≥ gcosα dla każdego kąta α. Prawa strona nierówności jest największa dla cosα = 1, czyli w najwyższym położeniu kamyka na okręgu, gdy α = 0. W tym położeniu musi być

ω²r ≥ g ,

ale gdy ta nierówność jest spełniona, to tym bardziej ω²r ≥ gcosα, dla α ≠ 0.

Prędkość kątowa ω, to stosunek przyrostu kąta do przyrostu czasu, czyli
. Kąt w tego typu obliczeniach liczy się w radianach, więc ω ma wymiar rad/s. 1 obrót to kąt pełny, czyli 2π rad. Prędkości obrotowej n obrotów na sekundę odpowiada prędkość kątowa ω = 2πn (rad/s). Stąd

(2πn)²r ≥ g,

a to oznacza
? (obrotów na sekundę!). Na minutę będzie 60 razy więcej obrotów, czyli odpowiednia prędkość obrotowa

 = ?

Krytycznym punktem jest „szczyt” okręgu. Gdy tam kamyk nie wypada, to nie wypadnie już nigdzie. W tym położeniu mamy od razu F_r = Q + R, czyli

R = F_r - Q = mω²r - mg.

Dalej już tak, jak poprzednio, czyli R ≥ 0, a stąd ω²r ≥ g itd.

25. Na nici o długości L₁ = 50 cm wisi mała kulka. Kulkę tę wprawiono w ruch po okręgu w płaszczyźnie poziomej tak, że nić zakreśla stożek a okres obrotu kulki wynosi T = 1,3 s. Jakie jest przyspieszenie dośrodkowe kulki? Jaka będzie prędkość liniowa kulki po skróceniu nici do długości L₂ = 45 cm, jeżeli częstotliwość obrotów nie zmieni się?

R. Przyspieszenie dośrodkowe obliczymy ze wzoru a_r = ω²·r, w którym ω oznacza prędkość kątową, a r jest promieniem okręgu. Prędkość kątową wyznaczamy ze związku ω = 2π/T, pozostaje znaleźć promień, który dla nici o długości L₁ oznaczymy przez r₁. Podczas ruchu kulki nić jest naprężona siłą N i odchylona od pionu o kąt α₁, taki, że r₁/L₁ = sinα₁. Kulka zakreśla więc okrąg o promieniu

r₁ = L₁·sinα₁. (1)

Pozioma składowa N_x naprężenia spełnia rolę siły dośrodkowej, czyli

N_x = F_r = ma_r = mω²·r₁. (2)

Przez m oznaczono masę kulki. Pionowa składowa N_y naprężenia równoważy siłę ciężkości, zatem

N_y = Q = mg. (3)

Z rysunku wynika, że N_x = Nsinα₁, N_y = Ncosα₁. Stąd oraz z (1), (2) i (3) wynikają równania

Nsinα₁ = mω²·L₁·sinα₁, (4)

Ncosα₁ = mg. (5)

Ponieważ 0 < α₁ < 90°, to sinα₁ ≠ 0 i z (4) dostajemy

N = mω²·L₁.

Po podstawieniu tego wyrażenia do (5) mamy mω²·L₁·cosα₁= mg, a stąd wyznaczamy

.

Ponieważ
, to z (1) wyznaczamy r₁ i otrzymujemy przyspieszenie dośrodkowe

?

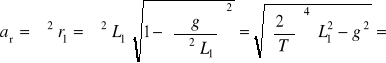
Prędkość liniową wyznaczamy ze związku v = ωr. Skoro po skróceniu nici częstotliwość obrotów nie zmieni się, to i okres będzie nadal ten sam. Kąt odchylenia nici od pionu i jej naprężenie mogą się jednak zmienić. Można powtórzyć kolejne kroki rozumowania dla krótszej nici i otrzymać cosinus nowego kąta odchylenia nici od pionu

.

Nowy promień okręgu wynosi r₂ = L₂·sinα₂, więc prędkość liniowa jest równa

?

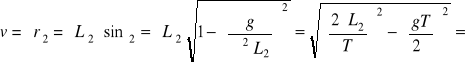
30. Ładunek o masie m = 10 kg był początkowo nieruchomy. Podniesiono go stałą siłą na wysokość h = 2 m w czasie t = 1,5 s. Obliczyć pracę jaką wykonano przy podnoszeniu. Z jaką mocą działano? Znaleźć rozwiązanie: a) bezpośrednio z określenia pracy b) z bilansu pracy i energii.

R. a) Chodzi o pracę, którą wykonuje siła podnosząca F na drodze s = h. Siła i przesunięcie mają ten sam kierunek i zwrot więc stosujemy najprostszy wzór, czyli W = Fs = Fh. Równanie dla tej siły jest takie, jak w zadaniu 22, gdzie siłą tą jest naprężenie linki, zatem ma = F - mg. Ponieważ
, to
, a stąd siła podnosząca wynosi
. Siła wykonała pracę
= ?, a rozwinięto moc P = W/t = ?

b) Gdy nie ma strat energii na tarcie i opór powietrza to praca = przyrost energii. Początkową energię potencjalną można przyjąć za E_p1 = 0. Nieruchomy początkowo ładunek miał także energię kinetyczną E_k1 = 0. Na wysokości h energia potencjalna wynosi E_p2 = mgh. Ładunek ma teraz prędkość
, a więc też energię kinetyczną
.

Przyrost energii wynosi
. Widać, że ΔE jest równe pracy W wyznaczonej w punkcie a).

31. Skrzynia o masie m = 15 kg stała na dole rampy nachylonej do poziomu pod kątem α = 25°. Współczynnik tarcia skrzyni o rampę wynosi μ = 0,5. Jaką pracę należy wykonać i jakiej mocy użyć, aby za pomocą stałej, równoległej do powierzchni rampy siły: a) wsunąć skrzynię na wysokość h = 2 m w czasie t = 4 s, b) zsunąć tę skrzynię z wysokości h = 2 m w czasie t = 4 s?

R. a1) Ponieważ
, to z definicji pracy W = F∙s, gdzie droga s = h/sinα. Siłę F liczymy z II zasady dynamiki ma = F - Q_x - T, przy czym Q_x = mgsinα, T = μmgcosα. Skoro F = const to a = const, zatem
,
, a stąd siła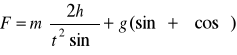
. Praca jest więc równa

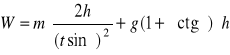
 = ?, użyta moc P = W/t = ?

a2) Z bilansu pracy i energii W_całk = ΔE, W_całk = W + W_T,  ΔE = E₂ - E₁, E₁ = 0 (jak w zadaniu 43.),
,
, praca siły tarcia W_T = 
= Tscosφ,  między wektorami
i
jest kąt φ = 180°, cosφ = -1, czyli W_T = Ts, więc wykonana praca

= ?

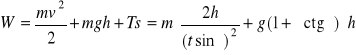
b1) Z definicji pracy jak w a1), ale II zasadę dynamiki wyraża równanie ma = F + Q_x - T, więc siła wynosi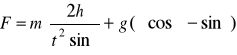
. Stąd praca i moc

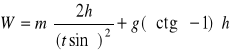
= ?, P = W/t = ?

b2) Z bilansu pracy i energii W_całk = W + W_T = E₂ - E₁, ale teraz E₁ = mgh,
. Zatem

= ?

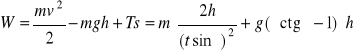
X

m₂

m₁

m₂

m₁

L₁

r₁

α₁

r

r

α

α

s

X

Y

Q_2x

T₂

Q₂

Q_2y

N'

h

Q_1x

Q_1y

T₁

Q₁

P'

α

m₂

m₁

s

X

Y

Q_2x

T₂

Q₂

Q_2y

N

h

Q_1x

Q_1y

T₁

Q₁

P

α

m₂

m₁

α

α

α

Q_x

Q_y

Q

β

C

B

A

α

α

X

Y

X

m₂

m₁

m

P'

P

s

z

d

δ

δ

x_końc

X

0

L₁

-L₂

X

0

L₁

-L₂

x_końc

X

0

L₂

-L₁

X

0

L₂

-L₁

---