Zespół Szkół nr 9 im. Romualda Traugutta
w Koszalinie
Temat: Badanie liczników TTL
Koszalin rok szk. 2002/200
Systemy zapisu liczb.
System dwójkowy zapisu liczb.
Liczby zapisuje się za pomocą cyfr i znaków pomocniczych. Powszechnie jest używany system dziesiętny zapisu (numeracji) liczb. Używa się w nim dziesięciu cyfr: 0,1,2,....,9; zapisy liczb interpretuje się zgodnie z podanymi przykładowo zależnościami:
(27)10 = 2∙ 10 + 7∙1
(325)10 = 3∙100 + 2∙10 +5∙1
(3,7)10 = 3∙1+ 7∙0,1
Konstrukcja cyfrowych urządzeń elektronicznych jest oparta na wykorzystaniu sygnałów logicznych, których wartości logiczne 0 (fałsz) i 1 (prawda) są interpretowane jako cyfry 0 i 1. Liczby są zapisywane przy użyciu tych dwóch cyfr. Na tak zapisanych liczbach można, jak się okazuje, wykonać takie same działania jak w systemie dziesiętnym, przy czym nawet samo wykonanie działań przebiegać może podobnie.
Do wykonywania działań na liczbach są stosowane układy logiczne. Ze względu na interpretowanie zmiennych logicznych jako cyfr, układy logiczne nazywa się także układami cyfrowymi.
Liczba dziesiętna (o podstawie liczenia dziesięć) jest po prostu ciągiem symboli, czyli cyfr, które są rozumiane jako mnożnik kolejnych potęg liczby 10, a cała liczba jest rozumiana jako suma tych iloczynów cząstkowych.
Na przykład: 137,06 = 1∙102 = 3∙101 + 7∙100 + 0∙10-1 +6∙10-2
Potrzeba na to 10 cyfr (od 0 do 9), a waga każdej cyfry jest określona jej położeniem względem przecinka dziesiętnego. Jeżeli chcemy reprezentować liczbę używając tylko dwóch symboli (0 i 1), musimy zastosować system dwójkowy liczenia (inaczej binarny), w którym podstawą jest cyfra 2. Cyfry 1 lub 0 mnoży się przez kolejne potęgi cyfry 2.
Na przykład: 11012 = 1∙23 + 1∙22 +0∙21 + 1∙20 = 1310
Poszczególne jedynki i zera są nazywane „bitami” (cyframi binarnymi). Dolny indeks określa obowiązujący system liczenia i jest często niezbędny dla uniknięcia niejednoznaczności, ponieważ stosowane w różnych systemach liczenia symbole wyglądają tak samo.
Liczbę dwójkową zamieniamy na dziesiętną metodą właśnie opisaną. Aby dokonać zamiany w przeciwnym kierunku, powtarzamy dzielenie liczby przez 2 i zapisujemy kolejne reszty. Aby zamienić liczbę 1310 na dwójkową wykonujemy dzielenie:
13:2 = 6 reszta 1
6:2 = 3 reszta 0
3:2 = 1 reszta 1
1:2 = 0 reszta 1
co daje 1310 = 11012. Zauważmy, że wynik otrzymujemy w kolejności od najmłodszego bitu (ang. least significant bit - LSB) do najstarszego bitu (ang. most significant bit - MSB).
Kodowanie BCD.
Innym sposobem zapisywania liczb jest dwójkowe kodowanie każdej cyfry dziesiętnej. Ten sposób nazywa się kodowaniem BCD (ang. binary coded decimal) i wymaga zastosowania grup 4- bitowych dla każdej cyfry dziesiętnej.
Na przykład: 13710 = 000100110111BCD
Zauważmy, że notacja BCD nie jest identyczna z zapisem dwójkowym, którym w tym przypadku jest 13710 = 100010012. Najlepiej uważać kolejne pozycje bitów (poczynając od prawego) za reprezentacje liczb 1,2,4,8, 10, 20, 40, 80, 100, 200, 400, 800, itd. W zapisie BCD marnotrawimy oczywiście część bitów, ponieważ każda grupo 4-bitowa mogłaby przedstawić liczby od 0 do 15, podczas gdy przedstawia tylko liczby od 0 do 9. Jednakże zapis BCD jest idealny, jeśli chce się wyświetlać liczby dziesiętne, ponieważ wszystko co trzeba zrobić, to zamienić każdą 4-bitową grupę BCD na odpowiadającą jej cyfrę dziesiętną i ją wyświetlić. Istnieje wiele układów specjalnie do tego przeznaczonych, np. dekoder, wzmacniacz i wyświetlacz BCD, który jest małym układem scalonym z przeźroczystym wierzchem. Doprowadza się do niego sygnały o poziomach logicznych odpowiednich dla pożądanej cyfry BCD i zapala się właściwa cyfra. Z tego powodu zapis BCD jest powszechnie używany do wprowadzania i wyprowadzania informacji numerycznych. Niemniej jednak arytmetyka binarna jest tak wydajna, że większość komputerów zmienia wszystkie dane wejściowe na postać binarną, przeprowadzając konwersję odwrotną tylko wtedy, gdy wymaga tego wyjście.
Liczby ze znakiem.
Zapis znak-moduł. Wcześniej czy później niezbędna staje się zapisywanie dwójkowe liczb ujemnych, szczególne w urządzeniach, które maja wykonać jakieś obliczenia. Najprostszą metodą jest poświęcenie jednego bitu (powiedzmy najstarszego - MSB) na znak, podczas, gdy pozostałe bity reprezentują moduł liczby. Ten sposób jest nazywany zapisem znak-moduł i odpowiada sposobowi, w jaki zwykle zapisywane są liczby ujemne. Jest on wykorzystywany zarówno przy wyświetlaniu liczb, jak i w niektórych przetwornikach A/C. Ogólnie możemy powiedzieć, że nie jest to najlepszy sposób zapisu liczb szczególnie, gdy mają być przeprowadzone jakieś obliczenia, i to z kilku powodów. Obliczenia są niewygodne, gdyż odejmowanie różni się od dodawania (tzn. dodawanie „nie działa” na liczbach ze znakiem). Pojawiają się także dwa zera (+0 i -0), więc należy dobrze uważać, aby używać tylko jednego z nich.
Zapis binarny przesunięty. Drugą metodą zapisu liczb ze znakiem jest zapis binarny przesunięty, w którym aby otrzymać reprezentowaną wartość, odejmuje się od niej połowę największej możliwej liczby. Ma to tę zaletę, że kody liczb od najbardziej ujemnej do najbardziej dodatniej tworzą zwykły binarny postęp arytmetyczny, odpowiadający w sposób naturalny trybowi liczników dwójkowych. Najstarszy bit w dalszym ciągu zawiera informację o znaku, a zero występuje tylko raz. Zapis binarny przesunięty jest popularny w przetwornikach A/C i C/A, ale wykonanie operacji arytmetycznych jest w nim w dalszym ciągu niewygodne.
Zapis z uzupełnieniem do dwóch. Najczęściej spotykamy w obliczeniach na liczbach całkowitych zapis z uzupełnieniem do dwóch. W tym zapisie liczby dodatnie są reprezentowane przez zwykłe liczby binarne bez znaku. Liczbę ujemną reprezentuje liczba binarna, którą trzeba dodać do liczby dodatniej o tym samym module, aby otrzymać zero. Aby zapisać liczbę ujemną, najpierw trzeba zanegować każdy bit liczby dodatniej (tzn. zastąpić 0 przez 1 i odwrotnie, do jest nazywane „uzupełnieniem do jedynki”), a następnie należy dodać (to jest „uzupełnić do dwóch”). Jak można wywnioskować z tablicy 1, związek pomiędzy zapisem z uzupełnieniem do 2 i zapisem binarnym przesuniętym polega na zanegowaniu najstarszego bitu (MSB). Podobnie jak dla innych sposobów przedstawiania liczb ze znakiem, również w tym przypadku MSB zawiera informację o znaku. Występuje tylko jedno zero, wygodnie reprezentowane przez same bity 0.
Liczba całkowita |
Znak-modulo |
Binarny przesunięty |
Z uzupełnieniem do 2 |
+7 |
0111 |
1111 |
0111 |
+6 |
0110 |
1110 |
0110 |
+5 |
0101 |
1101 |
0101 |
+4 |
0100 |
1100 |
0100 |
+3 |
001 |
1011 |
0011 |
+2 |
0010 |
1010 |
0010 |
+1 |
0001 |
1001 |
0001 |
0 |
0000 |
1000 |
0000 |
-1 |
1001 |
0111 |
1111 |
-2 |
1010 |
0110 |
1110 |
-3 |
1011 |
0101 |
1101 |
-4 |
1100 |
0100 |
1100 |
-5 |
1101 |
0011 |
1011 |
-6 |
1110 |
0010 |
1010 |
-7 |
1111 |
0001 |
1001 |
-8 |
- |
0000 |
1000 |
(-0) |
1000 |
- |
- |
Tabela 1. Trzy sposoby reprezentacji 4-bitowych liczb całkowitych ze znakiem.
Szesnastkowa (heksadecymalna) reprezentacja liczb.
Dla układów dwunastkowych najbardziej naturalnym sposobem zapisu liczb jest zapis binarny. Ponieważ liczby binarne są stosunkowo długimi ciągami cyfr, przyjęło się zapisywanie ich jako liczb szesnastkowych (o podstawie liczenia 16). Każda pozycja liczby szesnastkowej reprezentuje odpowiednią potęgę szesnastu, a symbol umieszczony na dowolnej pozycji ma wartość od 0 do 15. Ponieważ potrzebne są pojedyncze symbole umieszczane na pozycjach liczby szesnastkowej, wartościom od 10 do 15 przypisano symbole literowe od A do F. Aby liczbę binarną zamienić na szesnastkową (zapisać w postaci szesnastkowej), należy pogrupować ją, poczynając od najmniej znaczącego bitu, na fragmenty 4-bitowe i każdy taki fragment zapisać jako cyfrę szesnastkową np.:
70710 = 10110000112= 2C316
Reprezentacja szesnastkowa najbardziej odpowiada typowej bajtowej (8-bitowej) organizacji informacji we współczesnych komputerach, w których najczęściej występują „słowa” 16- lub 32-bitowe. Słowo składa się, zatem z dwóch lub czterech bajtów. Znak alfanumeryczny (litera, cyfra lub symbol) jest jednobajtowy. Tak więc w zapisie szesnastkowym każdy bajt składa się z dwóch cyfr szesnastkowych, słowo komputera 16-bitoergo z 4 cyfr szesnastkowych itd.
Liczniki.
Licznik służy do zliczania impulsów (zmian sygnału wejściowego) i pamiętania ich liczby. Na ogół ma on wyjście równoległe, na którym pojawia się informacja o liczbie zliczonych impulsów.
Każdy licznik na pewną pojemność P. Różnym liczbom impulsów wejściowych, różniącym się o wielokrotność P, odpowiada ten sam stan (zawartość) licznika. Liczba P jest również zwana okresem licznika; mówi się często, że licznik zlicz impulsy modulo P. Układ pamięciowy licznika jest zbudowany z przerzutników, a więc przy pojemności P trzeba użyć do budowy licznika, co najmniej N przerzutników, przy czym:
P≤ 2N
Liczbę N nazywa się długością licznika. Licznik o pojemności P przyjmuje P różnych kombinacji stanów N przerzutników, zgodnie z wynikającą z jego budowy kolejnością. Jedna z tych kombinacji jest przyjęta za zerową (początkową). Ustawienie jej za pomocą specjalnego wejścia nazywa się zerowaniem licznika. Wejście zerujące umożliwia wprowadzenie do licznika kombinacji zerowej niezależnie od aktualnej zawartości licznika. Po podaniu na wejście liczące P-1 zmian sygnału wejściowego licznik znajdzie się w stanie odpowiadającym ostatniej kombinacji. Pojawia się wtedy sygnał przeniesienia (przepełnienia;) przy pojawieniu się następnego impulsu wejściowego następuje wyzerowanie licznika.
Sygnał przeniesienia Y może mieć różną postać. Pokazano to na tys.1, na przykładzie licznika liczącego w naturalnym kodzie dwójkowym od 0 do 7 (P=9). Licznik tan składa się z trzech przerzutników Q0, Q1, Q2 (a więc N=3). przerzutniki zmieniają swój stan przy zmianie sygnału wejściowego z 1 na 0, dlatego też wspólną cechą narysowanych na rys.1 sygnałów przeniesień jest to, że wszystkie one zmieniają się z 1 na 0 w chwili wyzerowania się licznika.
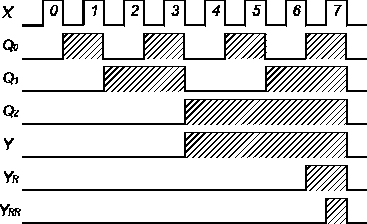
Rys. 1. Zasada działania licznika.
Pojawienie się sygnału YR=1 sygnalizuje znalezienie się licznika w stanie odpowiadającym ostatniej kombinacji kodu (w przypadku licznika dwójkowego- kombinacja 11...11). Sygnał YRR jest równy:
YRR= YRX
Liczniki o Pojemnościach P1, P2,......,Pk można łączyć ze sobą, otrzymując licznik o pojemności:
P=P1· P2· ..... ·Pk
Rozróżnia się dwa sposoby łączenia liczników:
szeregowe (licznik asynchroniczny),
równoległe (licznik synchroniczny).
Łączenie szeregowe liczników (rys. 2a) polega na tym, że wejście liczące X następnego licznika zostaje połączone z wyjściem przeniesienia Y poprzedniego licznika.
Ponieważ założono, że licznik zwiększa swoją zawartość przy zmianie sygnału X z 1 na 0, przy łączeniu szeregowym sygnałem przeniesienia Y może być dowolny sygnał, zmieniający się z 1na 0 w chwili wyzerowania się licznika, a więc którykolwiek z sygnałów z rys.1. Powrót poprzedniego licznika do zera, po przebiegnięciu całego okresu liczenia powoduje zwiększenie stanu następnego licznika o 1.
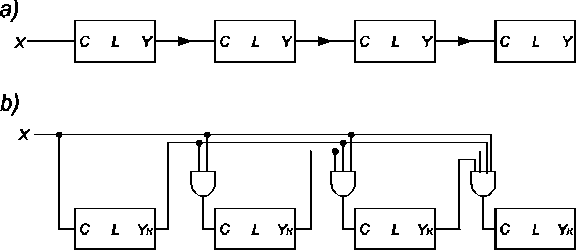
Rys. 2. Sposoby łączenia liczników: a) szeregowe; b) równoległe.
Ponieważ złażono, że licznik zwiększa swoją zawartość przy zmianie sygnału X z 1 na 0, przy łączeniu szeregowym sygnałem przeniesienia Y może być dowolny sygnał, zmieniający się z 1 na 0 w chwili wyzerowania się licznika, a więc którykolwiek z sygnałów Y z rys.1. Powrót poprzedniego licznika do zera, po przebiegnięciu całego okresu liczenia, powoduje zwiększenie stanu następnego licznika o 1.
Przy łączeniu równoległym sygnał wejściowy X jest podawany równocześnie na wszystkie liczniki (rys. 2b), przy czym dociera on do wejścia liczącego i-tego licznika, gdy wszystkie poprzednie liczniki są w stanach końcowych (odpowiadających ostatniej kombinacji kodu). Do łączenia równoległego liczników trzeba więc wytworzyć przeniesienie YR. Zaleta tego sposobu łączenia jest większa szybkość pracy układu, gdyż zmiana stanów wszystkich liczników następuje jednocześnie.
Ze względu na cechy oby systemów tworzenia liczników stosuje się często rozwiązania pośrednie. Człony składowe są budowane jako liczniki równoległe i łączone szeregowo (licznik szeregowo-równoległy). Sytuację odwrotną spotyka się rzadziej. Liczniki dziesiętne są budowane jako szeregowo-równoległe.
Jeśli wszystkie człony składowe mają pojemność równa 2, to cały licznik jest nazywany dwójkowym, a jego pojemność:
P=2N
Licznik dwójkowy stanowi często układ wyjściowy do tworzenia liczników o dowolnej pojemności.
Jeśli wszystkie człony składowe mają pojemność równą 10, to cały licznik jest nazywany dziesiętnym, a jego pojemność:
P=10N
Liczniki, oprócz wejścia liczącego i zerującego, mogą mieć również wyjście równoległe służące do wpisywania dowolnej wartości początkowej do licznika. Wpisywanie równoległe noże odbywać się niezależnie od zliczania (przy czym wtedy wpisywanie blokuje zliczanie) - takie wpisywanie będzie nazywane asynchronicznym. W wielu przypadkach korzystniejsze jest wpisywanie synchroniczne, odbywające się pod wpływem impulsów podawanych na wejście zegarowe. W zależności od sygnału na wejściu sterującym rodzaj pracy, impulsy wejściowe powodują bądź zwiększenie zawartości licznika o 1 (zliczanie), bądź też wpisanie równoległe informacji do licznika.
W wielu przypadkach buduje się liczniki o pojemnościach P nie będących ani potęgą 2 ani 10.Tworzenie liczników o dowolnej pojemności P odbywa się trzema sposobami:
przez zaprojektowanie odpowiedniego układu z przerzutników i elementów kombinacyjnych;
przez rozkład żądanej pojemności P na czynniki i łączenie gotowych członów o pojemnościach wynikających z tego rozkładu (nie zawsze jest to możliwe);
przez zmniejszenie pojemności licznika dwójkowego za pomocą sprzężenia zwrotnego;
Budowa liczników o dowolnej pojemności wg. drugiego sposobu opiera się na wykorzystaniu zasady łącznie członów. Pojemność licznika powstałego przez połączenie kilku członów jest równa iloczynowi pojemności tych członów
Metodę sprzężeń zwrotnych opisano w dalszej części instrukcji.
Dotychczas opisane liczniki odznaczają się tym, że zmiany sygnału wejściowego powodują przebieganie ciągu kombinacji kodu w jednym kierunku. Można budować liczniki zliczające w kierunku odwrotnym w tym samym zbiorze kombinacji przy zachowaniu ich uszeregowania. Jeden z kierunków jest definiowany jako prosty (licznik prosty), a drugi jako odwrotny (licznik odwrotny). Liczniki prosty i odwrotny są nazywane jednokierunkowymi. Oba rodzaje liczników buduje się tymi samymi metodami. Różnica między licznikiem prostym a odwrotnym uwidacznia się dopiero przy porównaniu dwóch liczników pracujących w tym samym kodzie.
W niektórych urządzeniach cyfrowych konieczne jest stosowanie liczników dwukierunkowych, tzn. mogących zliczać w jednym lub drugim kierunku. Liczniki dwukierunkowe lub rewersyjne są budowane w dwu wersjach, a mianowicie:
jako licznik o jednym wejściu sygnałów zliczanych oraz wejściu statycznym wybierającym kierunki;
jako licznik o dwu wejściach sygnałów zliczanych: jednym dla impulsów dodawanych do zawartości i drugim dla impulsów odejmowanych od zawartości.
Rewersję pracy licznika uzyskuje się przez łączenie przerzutników miedzy sobą układami, które mogą pracować jak w liczniku prostym lub jak w liczniku odwrotnym, w zależności od sygnału sterującego.
Podstawowymi parametrami licznika są:
maksymalna szybkość pracy - jest to maksymalna częstotliwość sygnałów wejściowych przy której licznik przyjmuje kolejno żądane stany. Wartość ta zależy głównie od parametrów użytych elementów.
czas ustalania zawartości licznika (T) - jest określony jako maksymalny okres między impulsem wyjściowym z ustaleniem się zawartości odpowiedniej dla danego przypadku. Czas ten jest różny dla różnych kombinacji zawartych w liczniku. Parametr ten w istotny sposób zależy od użytych podzespołów i od schematu logicznego licznika. Ogólnie rzecz biorąc, dla liczników szeregowych wyraża się on zależnością:
T ≈ τN
τ - czas propagacji przerzutnika.
Dla liczników równoległych obowiązuje zależność:
T ≈ τ
W dalszej części instrukcji są szczegółowo opisane trzy przykładowe liczniki, które zostały użyte w stanowisku pomiarowym. Są to:
7493 - asynchroniczny licznik dwójkowy (binarny), czterobitowy
7490 - dekada asynchroniczna (asynchroniczny licznik modulo 10)
74193 - synchroniczny, rewersyjny licznik dwójkowy (binarny), czterobitowy.
Liczniki asynchroniczne (MSI).
Sprzężenie zwrotne w licznikach.
Licznik 7493
Czterobitowy licznik dwójkowy 7493 i dekada 7490 należą do najprostszych liczników o średnim stopniu scalenia (MSI).
Moduł licznika dwójkowego 7493 (rys. 3) zawiera dwójkę liczącą i licznik szeregowy liczący do 8. Pierwsza dwójka może być wykorzystywana niezależnie bądź też połączona z wejściem C1 licznika liczącego do 8, tworząc licznik szeregowy liczący do 16. Wszystkie przerzutniki mają wspólne zerowanie, dołączone do elementu NAND z wejściami Z1 i Z2, wyzerowanie licznika następuje przy podaniu jedynki na oba wejścia zerujące. Wejście zerujące dominuje nad wejściami liczącymi C0 i C1, tzn. podanie sygnału zerującego powoduje wyzerowanie licznika niezależnie od sygnałów na wejściach liczących. Wejścia liczące zaczynają być czynne dopiero po pewnym czasie od chwili zniknięcia sygnału zerującego, tzn. zmiana sygnału C z 1 na 0 spowoduje zmianę zawartości licznika, jeżeli pojawia się po czasie tr (czas zwalniania) od chwili zniknięcia sygnału zerującego
R = Z1Z2
Parametry licznika takie jak: częstotliwość maksymalna zliczania i czas propagacji sygnału od wejścia C0 do wyjścia ostatniego przerzutnika Q3, są podane w katalogach.
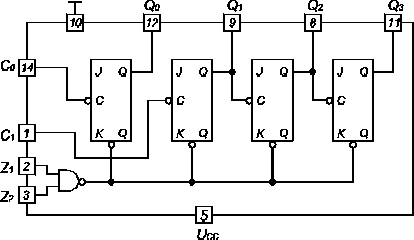
Rys. 3. Schemat licznika dwójkowego 7493.
Licznik 7490
Dekada 7490 (rys. 4) zawiera dwójkę licząca i licznik szeregowy liczący do 5. Licznik może pracować jako dekada licząca w naturalnym kodzie dwójkowym, 8421 - gdy wyjście pierwszej dwójki zostanie połączone z wejściem licznika liczącego do 5. Jeżeli połączy się wyjście Q3 licznika liczącego do 5 z wejściem C0 dwójki, to otrzyma się dekadę liczącą w kodzie 8421. Na wyjściu Q0 pojawi się wówczas przebieg prostokątny o wypełnieniu ½ i częstotliwości dziesięć razy mniejszej niż częstotliwość wejściowa. Reszcie liczniki liczące od 2 i do 5 mogą pracować niezależnie.
Dekada 7490 ma wejście zerujące identyczne jak w liczniku dwójkowym
R=Z1Z2
oraz wejście ustawiające
S= W1W2
powodujące ustawienie licznika w stan 9=1001. Wyzerowanie lub ustawienie następuje przy podaniu sygnałów 1 na oba wejścia Z1, Z2 lub W1, W2 (oczywiście nie wolno licznika jednocześnie zerować i ustawiać). Oba wejścia dominują nad wejściami liczącymi powodując zablokowanie licznika.
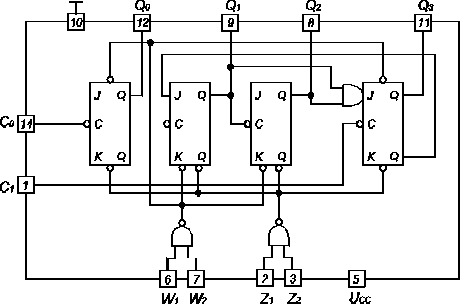
Rys. 4. Schemat dekady 7493.
Licznik rewersyjny 74193
Jako bloki funkcjonalne o średnim stopniu scalenia (MSI) są produkowane liczniki rewersyjne dwójkowe i dziesiętne z wejściami oby rodzajów wymienionych w p.1. Liczniki te z reguły mają wejścia równoległe, umożliwiające wpisywanie asynchroniczne lub synchroniczne informacji do licznika.
Licznik 74193 jest licznikiem z dwoma wejściami, a mianowicie z wejściem impulsów dodawanych do zawartości licznika C+ i wejściem impulsów odejmowanych C-. Ponadto licznik ten ma wpisywanie równoległe asynchroniczne. Licznik 74193 jest licznikiem dwójkowym o pojemności 16. schemat tego licznika podano na rys. 5; ma on następujące wejścia i wyjścia:
X0, X1, X2,X3 - wejście równoległe,
Q0, Q2, Q3, Q4 - wyjścia równoległe,
C+ - wejście impulsów dodawanych do zawartości licznika,
C- - wejście impulsów odejmowanych od zawartości licznika,
Y+ - wyjście przeniesienia
Y- - wyjście pożyczki
L - wpisywanie asynchroniczne
R - zerowanie asynchroniczne
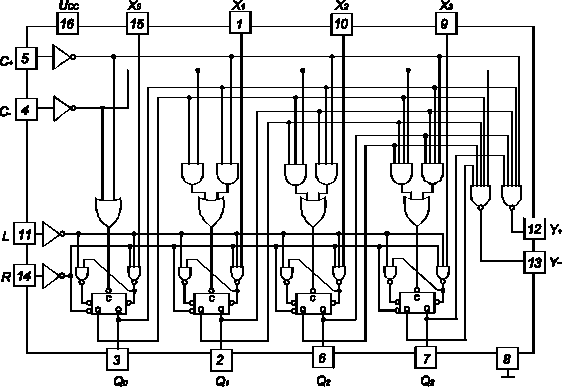
Rys. 5. Schemat licznika rewersyjnego 74193
Podanie sygnału R=1 powoduje wyzerowanie licznika, niezależnie od stanu pozostałych wejść. Podanie sygnału L=0 powoduje wpisanie liczby X0, X1, X2,X3 do licznika, niezależnie od sygnałów na wejściach liczących. Zerowanie dominuje więc nad wszystkimi innymi sygnałami, a wpisywanie nad zliczaniem.
Przy zliczaniu impulsów wejściowych licznik zmienia swój sta przy zmianie sygnału C+ lub C- z 0 na 1. Jeśli są podawanie impulsy C+, to na wejściu C- powinien być sygnał 1 i odwrotnie.
Przykładowy cykl pracy licznika pokazano na rys. 6. Licznik jest zerowany, następnie wpisuje się do niego liczbę 13 i podane na wejście impulsy C+. Po osiągnięciu stanu 15 licznik wraca do zera, w chwili, gdy stan jego jest równy 15 i przychodzi impuls C+ = 0 pojawia się sygnał przeniesienia Y+ = 0. Licznik liczy dalej „w przód”, gdy osiągnie stan 2, przestaje się podawać impulsy C+, a zaczyna się podawać impulsy C-. Licznik zmniejsza swoją zawartość, gdy osiągnie stan 0 i przyjdzie impuls C+ = 0, pojawia się sygnał pożyczki Y- = 0.
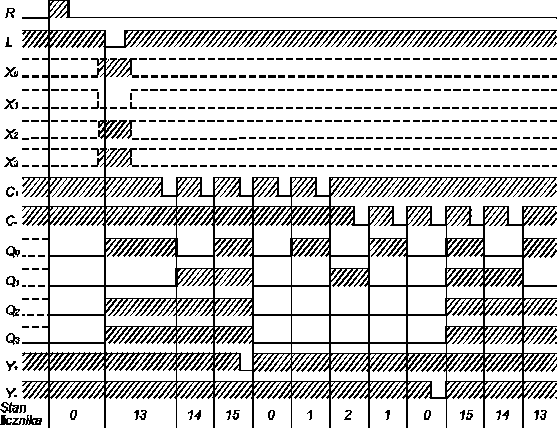
Rys. 6.Przebiegi czasowe w liczniku 74193
W punkcie tym omówiono sposoby zmieniania pojemności licznika przez wprowadzenie sprzężenia zwrotnego zerującego ten licznik lub ustawiającego go w określony stan. ten sposób zmiany pojemności licznika ma szczególne znaczenie przy korzystaniu z gotowych bloków funkcjonalnych MSI, gdyż liczniki MSI są budowane zazwyczaj jako moduły o pojemności P=16 lub P=10.
W najprostszym przypadku sprzężenie zwrotne wprowadza się w ten sposób, że dekoduje się określony stan licznika za pomocą elementu iloczynu i sygnałem z wyjścia tego elementu zeruje się liczniki lub ustawia go w określony inny stan (przy użyciu wejść statycznych przerzutników). Sprzężenie takie działa niepewnie, gdyż np. w przypadku zerowania, wyzerowanie jednego przerzutnika, którego wyjście jest podane na element dekodera, wystarczy do zniknięcia sygnału zerującego, gdy tymczasem inne przerzutniki mogły się jeszcze nie zdążyć wyzerować. Tego typu bezpośrednie sprzężenie można stosować tylko do liczników zbudowanych jako bloki funkcjonalne MSI, gdyż wszystkie przerzutniki w bloku mają zbliżone parametry.
W celu zwiększenia pewności działania należy wprowadzić do sprzężenia zwrotnego opóźnienie w postaci przerzutnika. Przerzutnik ten zapamiętuje sygnał pojawiający się na wyjściu elementu dekodera do chwili przyjęcia następnego impulsu wejściowego, zapewniając ty samym niezawodne wyzerowanie lub ustawienie licznika.
W licznikach z wpisywaniem synchronicznym lub zerowaniem nie jest wymagane żadne opóźnienie w torze sprzężenia zwrotnego, jeśli jest one podane na wejście sterujące rodzaj pracy licznika.
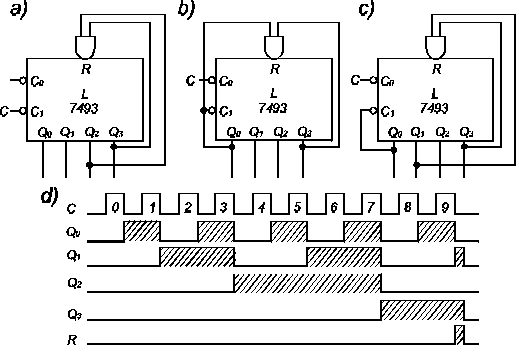
Rys. 7. Przykładowe zastosowanie sprzężenia zwrotnego w liczniku 7493 o pojemności: a) 6; b) 9; c) 10. d) wykres czasowy dla układu c.
Spis treści:
2
3
Badanie liczników TTL.
2
12
Badanie liczników TTL.
13
Teoria.
Wyszukiwarka