WIADOMOŚCI WSTĘPNE

1. PODSTAWOWE STRUKTURY ALGEBRAICZNE

1. Definicja Działaniem 2-argumentowym na niepustym zbiorze A nazywamy dowolne odwzorowanie Wartość f(a,b) nazywamy rezultatem (wynikiem) działania f na elementach a, b ze zbioru A.

2. Jeśli f jest działaniem w A, X ⊆ A oraz dla dowolnych elementów x, y ∈ X f(x,y) ∈ X, to mówimy, że zbiór X jest zamknięty ze względu na działanie f. Możemy wtedy zdefiniować działanie g na X, g(x,y) := f(x,y), dla x, y ∈ X.

3. Przykłady : + , −, ⋅ są działaniami w zbiorze liczb rzeczywistych R. Podzbiór N zbioru R jest zamknięty ze względu na + oraz ⋅ a nie jest zamknięty ze względu na −.

4. Definicja Grupą nazywamy parę (G,•), gdzie G jest niepustym zbiorem a • jest działaniem 2-argumentowym w G, takim że następujące warunki są spełnione:

G1. x•(y•z) = (x•y) •z (łączność •)

G2. x•e = e•x = x (istnienie elementu neutralnego)

G3. x•x^-1 = x^-1•x = e (istnienie elementu odwrotnego).

5. Przykłady : (R,+), (Q,+), (Z,+), (r-{0}, ⋅), ({x∈R; x > 0}, ⋅}

1.6. Definicja . Niech (G,•) będzie grupą a H podzbiorem G, takim że e ∈ H oraz dla dowolnych x, y ∈ H element x•y ∈ H. Jeżeli H wraz z działaniem • grupy (G,•) jest grupą to mówimy, że (H,•) jest podgrupą grupy (G,•).

TWIERDZENIE. Niech (G,•) będzie grupą a H niepustym podzbiorem G. (H,•) jest podgrupą grupy (G,•) wtedy i tylko wtedy gdy dla dowolnych x, y ∈ H element x•y^-1 ∈ H.

1.7. DEFINICJA. Ciałem nazywamy trójkę (K,+, ⋅), taką że

C1. (K,+) jest grupą przemienną z elementem neutralnym 0.

C2. (K-{0},⋅) jest grupą przemienną .

C2. x ⋅ (y + z) = x ⋅ y + x ⋅ z (rozdzielność mnożenia względem dodawania).

1.8. PRZYKŁADY. Ciało liczb rzeczywistych (R, +, ⋅), ciało liczb wymiernych (Q,+, ⋅).

2. GRUPY PERMUTACJI

1. Niech A = {1, ...,n} oraz S_n := {f: A → A, f odwracalne}. Wtedy (S_n, •) gdzie • jest składanie odwzorowań jest grupą. Nazywamy ją grupą permutacji zbioru n-elementowego A. Niech a, b ∈ A oraz a ≠ b. Transpozycją nazywamy permutację τ ∈ S_n zdefiniowaną następująco

τ(x) = . Permutację τ oznaczamy <a,b>.

2. TWIERDZENIE. Każdą permutację ze zbioru S_n można przedstawić jako złożenie skończonej liczby transpozycji.

TWIERDZENIE. Każdą transpozycję można przedstawić jako złożenie nieparzystej liczby transpozycji wyrazów sąsiednich ( <k,k+1>)

3. LEMAT. Niech P: S_n → Z, P(σ) :=
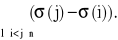
   Wtedy dla dowolnej permutacji σ i dowolnej transpozycji τ ze zbioru S_n , P(σ•τ) = − P(σ).

TWIERDZENIE. Niech σ ∈ S_n. Jeśli σ =
oraz σ =
, gdzie
są transpozycjami z S_n, to (-1)^r = (-1)^s.

DEFINICJA. Niech σ ∈ S_n i σ =
gdzie
są transpozycjami z S_n. Liczbę (-1)^r nazywamy znakiem permutacji σ i oznaczamy sgnσ. Jeśli sgnσ = 1 to permutację σ nazywamy permutacją parzystą, Jeśli sgnσ = -1 to permutację σ nazywamy permutacją nieparzystą,

3. LICZBY ZESPOLONE

1. DEFINICJA Liczbą zespoloną nazywamy uporządkowaną parę liczb rzeczywistych. Zbiór wszystkich liczb zespolonych oznaczamy przez C. Mamy zatem C:= {z=(x,y) : x,y ∈ R}. Niech z₁ = (x₁,y₁), z₂ = (x₂,y₂) będą liczbami zespolonymi.

Sumę liczb zespolonych określamy wzorem: z₁ + z₂ := (x₁ + x₂, y₁ + y₂).

Iloczyn liczb zespolonych określamy wzorem: z₁ ⋅ z₂ := (x₁x₂ - y₁y₂, x₁y₂ + x₂y₁).

2. FAKT (Własności działań w zbiorze liczb zespolonych). Niech z = (x,y) oraz z_1, z₂, z₃ będą dowolnymi liczbami zespolonymi. Wtedy

1. dodawanie liczb zespolonych jest przemienne, tzn. z₁ + z₂ = z₂ + z₁;

2. dodawanie liczb zespolonych jest łączne, tzn. (z₁ + z₂) + z₃ = z₁ + (z₂ + z₃);

3. liczba zespolona 0:= (0,0) jest elementem neutralnym dodawania, tzn. 0 + z =z;

4. dla każdej liczby zespolonej z istnieje liczba -z := (-x,-y), taka że z + (-z) = 0;

5. mnożenie liczb zespolonych jest przemienne, tzn. z₁⋅z₂ = z₂ ⋅z_1;

6. mnożenie liczb zespolonych jest łączne, tzn. (z₁⋅z₂)⋅z₃ = z₁⋅(z₂⋅z₃);

7. liczba zespolona 1 := (1,0) jest elementem neutralnym mnożenia, tzn. z⋅1 = z;

8. dla każdej liczby zespolonej z ≠ 0 istnieje liczba z^-1 :=
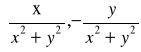
   odwrotna do niej, tj. taka że z^-1⋅z = 1;

9. mnożenie liczb zespolonych jest rozdzielne względem dodawania, tzn. z₁⋅(z₂ + z₃) = z₁⋅z₂ + z₁⋅z₃.

FAKT. (C, +, ⋅) jest ciałem.

3.3. Liczbę zespoloną (0,1) nazywamy jednostką urojoną i oznaczamy ją przez i; i := (0,1). Liczba i jest pierwiastkiem równania x² + 1 = 0. Każdą liczbę zespoloną postaci (a,0) utożsamiamy z liczbą rzeczywistą a. Po tym utożsamieniu każdą liczbę zespoloną (x,y) można jednoznacznie przedstawić w postaci z = x + yi, gdzie x, y ∈R. Ten sposób przedstawienia liczb zespolonych nazywa się ich postacią algebraiczną.

MACIERZE I WYZNACZNIKI

1. OPERACJE NA MACIERZACH.

1.1. DEFINICJA. Niech K = (K, +, ⋅) będzie ciałem. Macierzą typu m×n nad K lub m×n - macierzą nad K nazywamy funkcję A: {1, ..., m} × {1, ..., n} → K.

Najczęściej zamiast A(i,j) piszemy a_ij dla i ∈ {1, ..., m} oraz j ∈ {1, ..., n} i przedstawiamy macierz A w postaci tablicy

A =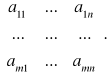

Wartości a_ij nazywamy wyrazami macierzy A. Często piszemy krócej A =
lub A =
. Symbolem
będziemy oznaczali zbiór wszystkich macierzy typu m × n nad K.

Niech A ∈
oraz niech i₁, ...,i_p ∈ {1, ..., m} i j₁, ...,j_r ∈ {1, ..., n}. Wtedy p × r macierz B, taką że B(k,l) := A(i_k,j_l) dla k = 1, ...,p, j = 1,... ,r oznaczamy symbolem . W przypadku gdy (i₁,...,i_p) = (1,...,m) zamiast piszemy , a gdy (j₁,...,j_r) = (1,...,n) zamiast piszemy . Jeśli 1 ≤ i₁ < ... <i_p ≤ m oraz 1 ≤ j₁ < ... <j_r ≤ n, to nazywa się podmacierzą macierzy A. Podmacierze typu 1 × n nazywamy wierszami a podmacierze typu m × 1 kolumnami macierzy A. Oznaczamy je odpowiednio: c^j(A) = A^(j) = j-ta kolumna macierzy A oraz r_i(A) = A_(i) = [a_i1...a_in] i-ty wiersz macierzy A.

Niech A ∈ , B ∈ . Wtedy symbolem AB będziemy oznaczali m × (n + p)-macierz taką że c^j(AB) = .

Niech A ∈ , C ∈ . Wtedy symbolem oznaczamy (m + r) × n-macierz, taką że r_i() = .

Każdą macierz n × n nazywamy macierzą kwadratową. Wyrazy a₁₁, ...,a_nn tworzą główną przekątną macierzy A.

Macierz kwadratową której wszystkie wyrazy poza główną przekątną są równe 0 nazywamy macierzą diagonalną. Macierz diagonalną mającą wyrazy a₁, ..., a_n na głównej przekątnej oznaczamy symbolem diag(a₁, ..., a_n).

1.2. DEFINICJA. Niech A, B ∈ , c ∈ K. Sumą macierz A i B nazywamy m × n macierz A + B, (A + B)(i,j) := A(i.j) + B(i,j), i = 1,...,m, j = 1, ...,n. Iloczynem macierzy A przez c nazywamy m × n macierz cA, cA(i,j) := cA(i,j), i = 1,...,m, j = 1, ...,n.

Symbolem lub 0 oznaczamy macierz której wszystkie wyrazy są równe 0.

TWIERDZENIE. Niech A, B, C ∈ , a, b ∈ K. Wtedy:

1. 0 + A = A + 0, A + (-1)A = 0,

1. (A + B) + C = A + (B + C),

2. A + B = B + A,

3. 1A = A,

4. a(bA) = (ab)A,

5. (a + b)A = aA + bA, a(A + B) = aA +aB.

TWIERDZENIE. (,+) jest grupą przemienną.

Macierz (-1)A oznaczamy -A.

1.3. DEFINICJA. Niech A ∈ , B ∈ . Iloczynem macierzy A i B nazywamy macierz C typu m × p nad K, taką że C(i,j) = , dla i = 1 ,..., m, j = 1 ,..., p. Iloczyn macierzy A i B oznaczamy symbolem AB.

TWIERDZENIE. Niech A, A'∈ , B, B' ∈ , C ∈ , a ∈ K. Wtedy

1. (AB)C = A(BC),

1. (A + A')B = AB + A'B oraz A(B + B') = AB + AB',

2. (aA)B = A(aB) = a(AB),

3. I_mA = A = AI_n , gdzie I_n ∈ oraz I_n = diag(1,...,1).

1.4. TWIERDZENIE. Jeśli A ∈ i B ∈ , to

1. c^j(AB) = Ac^j(B) dla j = 1, ..., p,

1. r_i(AB) = r_i(A)B dla i = 1, ..., m.

WNIOSEK. Jeśli A ∈ i B ∈ , to

1. c^j(AB) = dla j = 1, ..., p,

1. r_i(AB) = dla i = 1, ..., m.

TWIERDZENIE. Niech A ∈ oraz B ∈ . Jeśli {k₁, ..., k_r} ∪ {l₁,...,l_p} = {1, ...,n}, gdzie n = p + r, to AB = .

1.5. DEFINICJA. Niech A ∈ . Macierz A nazywamy macierzą odwracalną, jeśli istnieje macierz B ∈ , taka że AB = BA = I_n. Macierz B spełniającą powyższy warunek nazywamy macierzą odwrotną do A i oznaczamy symbolem A^-1.

TWIERDZENIE. Zbiór wszystkich odwracalnych macierzy n × n nad ciałem K tworzy grupę ze względu na mnożenie macierzy oraz:

1. macierz I_n jest macierzą odwracalną i (I_n)^-1 = I_n,

1. jeśli A jest macierzą odwracalną to A^-1 jest macierzą odwracalną i (A^-1)^-1 = A,

2. jeśli A, B są odwracalnymi macierzami n × n nad ciałem K, to AB jest macierzą odwracalną i (AB)^-1= B^-1A^-1.

1.6. DEFINICJA. Niech A ∈ . Macierzą transponowaną do macierzy A nazywamy macierz A^T∈ , taką że A^T(i,j) := A(j,i) dla i = 1, ...,n, j = 1,..., m. Odwzorowanie przyporządkowujące macierzy A macierz A^T nazywamy transpozycją.

TWIERDZENIE. Niech A , B ∈ , c ∈ K. Wtedy

1. (A + B)^T = A^T + B^T,

1. (cA)^T = cA^T,

2. (A^T)^T = A,

3. I^T = I.

TWIERDZENIE. Niech A ∈ oraz B ∈ . Wtedy (AB)^T = B^TA^T.

TWIERDZENIE. Jeśli macierz A jest odwracalna, to macierz A^T jest również odwracalna i (A^T)^-1 = (A^-1)^T.

2. Operacje Elementarne

2.1. DEFINICJA. Elementarnymi operacjami na wierszach macierzy A o współczynnikach w ciele K nazywamy:

1. mnożenie dowolnego wiersza macierzy przez niezerowy element ciała,

1. dodawanie do dowolnego wiersza macierzy dowolnego innego pomnożonego przez dowolny element ciała K,

2. zamianę dwóch różnych wierszy miejscami .

Będziemy posługiwali się następującymi oznaczeniami:

A A' oznacza, że macierz A' powstaje z macierzy A przez pomnożenie i-tego wiersza przez element a ∈ K, (a ≠ 0)

A A' oznacza, że macierz A' powstała z macierzy A w wyniku dodania do i-tego wiersza macierzy A wiersza k-tego A pomnożonego przez a ∈ K, gdzie i ≠ k,

A A' oznacza, że macierz A' powstała z macierzy A przez zamianę miejscami wierszy i-tego oraz k-tego (gdzie i ≠ k).

Analogicznie definiujemy operacje elementarne na kolumnach A.

TWIERDZENIE. Dla każdej operacji elementarnej istnieje odwrotna do niej operacja będąca operacją elementarną tego samego typu.

2.2. TWIERDZENIE. Niech f będzie złożeniem skończonej liczby operacji elementarnych na wierszach oraz g będzie złożeniem skończonej liczby operacji elementarnych na kolumnach macierzy. Wtedy

f(AB) = f(A)B oraz g(AB) =Ag(B),

dla dowolnych macierzy A i B (oczywiście jeśli zdefiniowany jest iloczyn AB).

WNIOSEK. Niech A ∈ oraz niech f będzie złożeniem skończonej liczby operacji elementarnych na wierszach a g będzie złożeniem skończonej liczby operacji elementarnych na kolumnach macierzy. Wtedy

f(A) = NA, gdzie N = f(I_m)

g(A) = AN, gdzie N = g(I_n).

WNIOSEK. Jeśli f jest złożeniem skończonej liczby operacji elementarnych na wierszach i N = f(I), to N jest macierzą odwracalną i N^-1 = f^-1(I).

2.3. TWIERDZENIE. Niech f będzie operacją elementarną na wierszach a g będzie operacją elementarną na kolumnach macierzy. Wtedy jeśli A = (B C), to f(A) = (f(B)f(C)) oraz jeśli A =

TWIERDZENIE. Niech A ∈ oraz niech f będzie złożeniem skończonej liczby operacji elementarnych na wierszach. Jeśli f(AI) = (IB), to B = A^-1. Podobnie jeśli g jest złożeniem skończonej liczby operacji elementarnych na kolumnach i g, to B = A^-1.

2.4 DEFINICJA. Macierzą elementarną nazywamy każdą macierz otrzymaną w wyniku wykonania jednej elementarnej operacji na wierszach macierzy jednostkowej.

TWIERDZENIE. Niech E będzie macierzą elementarną. Wtedy

1. E jest macierzą odwracalną oraz E^-1 jest macierzą elementarną,

1. E^T jest macierzą elementarną.

3. MACIERZE RÓWNOWAŻNE

3.1.DEFINICJA. Mówimy, że macierz A' jest wierszowo równoważna (kolumnowo równoważna) macierzy A i piszemy A' ≈_w A (A' ≈_k A), jeśli A' można otrzymać z A przy pomocy skończonej liczby operacji elementarnych na wierszach (kolumnach).

TWIERDZENIE. Relacje ≈_w i ≈_k są relacjami równoważności na zbiorze .

TWIERDZENIE. A' ≈_w A ⇔ istnieje skończony ciąg E₁, ..., E_k macierzy elementarnych, takich że A' = E₁...E_kA. Podobnie, A' ≈_k A ⇔ istnieje skończony ciąg E₁, ..., E_k macierzy elementarnych, takich że A' = AE₁...E_k.

3.2. DEFINICJA. Niech A ∈ . Macierz A nazywamy macierzą wierszowo zredukowaną, jeśli istnieje liczba całkowita r, 1 ≤ r ≤ m, oraz liczby całkowite k₁, ... , k_r , 1 ≤ k₁ < ... < k_r ≤ n, takie że

1. ,

1. jeśli r < m, to A_(r+1,...,m) = 0.

TWIERDZENIE. Jeśli A jest odwracalną macierzą wierszowo zredukowaną to A = I.

TWIERDZENIE. Każda niezerowa macierz A ∈ jest wierszowo równoważna pewnej macierzy wierszowo zredukowanej.

3.3. TWIERDZENIE. Niech A ∈ .Wtedy następujące warunki są równoważne:

1. A jest macierzą odwracalną,

1. A jest wierszowo równoważna macierzy jednostkowej,

2. A jest iloczynem macierzy elementarnych,

3. A jest kolumnowo równoważna macierzy jednostkowej.

4. WYZNACZNIKI

4.1. DEFINICJA. Niech A ∈ . Wyznacznikiem macierzy A nazywamy element ciała K, DetA :=

LEMAT. Niech A ∈ . Wtedy DetA =

TWIERDZENIE. Jeśli A ∈ , to DetA = DetA^T.

4.2. TWIERDZENIE. Niech A ∈ , α ∈ S_n, a ∈ K. Wtedy:

1. DetA^{(α(1),..., α(n))} = sgnαDetA,

1. Det(A⁽¹⁾,...,aA^(j),...,A⁽ⁿ⁾) = aDet(A⁽¹⁾,...,A^(j),...,A⁽ⁿ⁾),

2. Det(A⁽¹⁾,..., A^(j)+A'^(j), ...,A⁽ⁿ⁾) = Det(A⁽¹⁾,..., A^(j), ...,A⁽ⁿ⁾) + Det(A⁽¹⁾,..., A'^(j), ...,A⁽ⁿ⁾),

3. Jeśli macierz A ma dwie jednakowe kolumny (wiersze), to DetA = 0.

WNIOSEK.

1. Jeśli w macierzy A zmienimy kolejność kolumn (wierszy), to wyznacznik zmieni znak.

1. Wyznacznik macierzy nie ulegnie zmianie jeśli do dowolnej kolumny macierzy dodamy inną pomnożoną przez dowolny element ciała.

TWIERDZENIE. Niech A, B ∈ . Wtedy Det(AB) = DetADetB.

4.3. DEFINICJA. Dopełnieniem algebraicznym wyrazu a_ij macierzy A nazywamy element ciała K oznaczany A_ij, A_ij := (-1)^i+jDet
. Macierz nazywamy się macierzą dopełnień macierzy A i oznaczamy A^D.

LEMAT. Niech A = [a_ij]_nⁿ oraz r_i(A) = [0,...,0,a_ij,0,...,0]. Wtedy

DetA = a_ijA_ij = a_ij(-1)^i+jDet
.

TWIERDZENIE. Niech A = [a_ij]_nⁿ. Wtedy dla dowolnego i, j = 1, ...,n

1. DetA = a_i1A_i1 + ... + a_inA_in, (rozwinięcie Laplace'a wyznacznika A względem i-tego wiersza)

1. DetA = a_1jA_1j + ... + a_njA_nj, (rozwinięcie Laplace'a wyznacznika A względem j-tej kolumny).

4.4. TWIERDZENIE. Niech A = [a_ij]_nⁿ. Wtedy macierz A jest odwracalna wtedy i tylko wtedy gdy DetA ≠0. Ponadto, jeśli DetA ≠0, to A^-1 = A^D(DetA)^-1, oraz DetA^-1 = (DetA)^-1.

Układy Równań liniowych

1. DEFINICJA. Układem m równań liniowych z n niewiadomymi o współczynnikach w ciele K nazywamy każdy układ równań postaci:

(*)
,

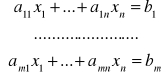
gdzie a_ij , b_i ∈ K, dla i =1,..., m, j = 1, ..., n.

Jeśli dla dowolnego i, b_i = 0, to układ (*) nazywamy układem jednorodnym.

Dowolny ciąg x₁, ...,x_n elementów z ciała K spełniający (*) nazywamy rozwiązaniem układu.

Macierz A =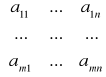
nazywamy macierzą układu, macierz B =
macierzą wyrazów wolnych, a macierz (AB) macierzą rozszerzoną układu.

Rozw(AB) oznacza zbiór wszystkich rozwiązań układu równań liniowych o macierzy rozszerzonej (AB), (u.r.l. (AB)).

Ciąg (x₁, ...,x_n) jest rozwiązaniem u.r.l. (AB) ⇔ macierz [x₁, ...,x_n]^T jest rozwiązaniem równania macierzowego AX = B.

2. Będziemy teraz rozwiązywać równania macierzowe postaci AX = B, gdzie A ∈ , oraz B ∈ Oczywiste jest że szukana macierz X ∈

Jeśli q = 1, to otrzymujemy układ równań liniowych.

TWIERDZENIE. Niech A, A'∈ , B, B'∈ Jeśli A'B' ≈_w AB, to macierz X jest rozwiązaniem równania AX = B wtedy i tylko wtedy, gdy X jest rozwiązaniem równania A'X = B'.

WNIOSEK. Jeśli A'B' ≈_w AB, to Rozw(A'B' ) = Rozw(AB).

3. Niech A ∈ , B ∈ , oraz niech AB ≈_w A'B', gdzie macierz A' jest wierszowo zredukowana. Niech r będzie liczbą niezerowych wierszy macierzy A'. Wtedy istnieją 1 ≤ j₁ < ... < j_r ≤ n, takie że Jeśli r = n, to 1= j₁, ..., j_n = n. Jeśli r < n to p = n-r oraz niech k₁, ...,k_p będą ustawionymi w porządku rosnącym numerami pozostałych kolumn A', tj. 1 ≤ k₁ < ... < k_p ≤ n, oraz {j₁ ,... ,j_r }∪ { k₁ , ... , k_p} = {1, ... ,n}.

TWIERDZENIE. Przy powyższych oznaczeniach otrzymujemy:

I. Jeśli r < m i B'_(r+1,...,m) ≠ 0, to równanie AX = B nie ma rozwiązań.

II. Jeśli r = m lub r < m i B'_(r+1,...,m) ≠ 0, to równanie AX = B ma conajmniej jedno rozwiązanie, przy czym:

1. Jeśli r = n, to rozwiązanie jest dokładnie jedno i ma postać X = B'_(1,...,n).

2. Jeśli r < n, to dla dowolnej p × q macierzy S o współczynnikach w K macierz X zdefiniowana następująco: jest rozwiązaniem AX = B i nie ma innych rozwiązań.

4. TWIERDZENIE (Cramera). Niech A = [a_ij]_nⁿ oraz b ∈ . Układ równań Ax = b ma dokładnie jedno rozwiązanie wtedy i tylko wtedy gdy DetA ≠0. Wtedy x = [x₁,...x_n]^T, x_j = DetB_j(DetA)^-1, gdzie B_j = (A⁽¹⁾,...,A^(j-1),b,A^(j+1),...,A⁽ⁿ⁾) jest rozwiązaniem tego układu.

1

3

---