RACHUNEK CAŁKOWY FUNKCJI WIELU ZMIENNYCH

I. CAŁKI PODWÓJNE

Niech dana jest funkcja ograniczona:

:

.

W celu zdefiniowania całki podwójnej funkcji f(x,y) w obszarze ograniczonym i regularnym D
R postępujemy następująco:

1^o Dzielimy obszar D na n podobszarów D_i takich, by
D_i=D , D

D_j = 0,
odpowiednio o polach

_i.

2^o W każdym podobszarze D
wybieramy w dowolny sposób punkt P_i (

,
_i)

(i=1,2 ... n).

3^o Tworzymy sumę całkową Riemanna w następujący sposób:

S_n =
f(
_i,
_i)

_i

(wartość funkcji mnożymy przez długość pola i sumujemy).

DEFINICJA:

Jeżeli przy dowolnym ciągu {
_n} normalnym podziałów obszaru D na podobszary D_i [
(
) = 0] i przy dowolnym doborze punktów P_i (
_i,
_i)
D_i ciąg sum całkowych
dąży stale do tej samej skończonej granicy I tj. S_n
I, to mówimy, że została określona całka podwójna z funkcji f(x,y) w obszarze D.

Symbolicznie:

, gdzie
[średnica podziału D na podobszary D_i (i = 1...n)],

czyli

.

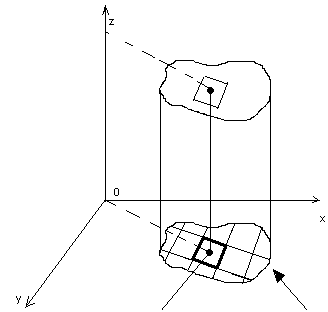
c.d. DEF.

Dowolny punkt P_i = (
_i,
_i)
D_i , gdzie D_i są podobszarami o polach
, na które został podzielony obszar D ( i=1,2,...,n).

W interpretacji geomertrycznej całka podwójna

oznacza objętość bryły ograniczonej powierzchnią
i obszarem płaskim D.

W ogólności:

V =

Jeżeli
1, to liczbowo:

V = P =

Zatem pole obszaru płaskiego D wyliczamy ze wzoru:

P(D) =

Jeżeli
>0 jest gęstością masy w obszarze D, to całkowita masa skupiona w tym

obszarze jest określona wzorem:

Wszystkie podstawowe własności całki podwójnej są analogiczne jak przy całce pojedynczej.

TWIERDZENIE 1:

Jeżeli
ciągła w obszarze D, gdzie D jest obszarem normalnym względem osi OX lub OY, to:

1^o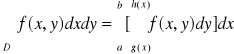
,

gdy D = D_x = {
- jest obszarem normalnym względem osi OX.

2^o Całka

,

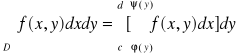
gdy D = D_y =
- jest obszarem normalnym względem osi OY.

WNIOSEK 1:

Jeżeli D = D_x = D_y, to 1^o = 2^o .

WNIOSEK 2:

Jeżeli D = P =
jest prostokątem, to

=
.

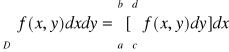
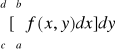
Jeśli ponadto
, to

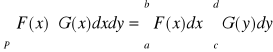
PRZYKŁAD 1:

Oblicz pole obszaru ograniczonego krzywymi: x = y², y = x²

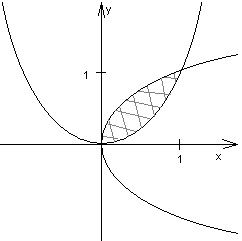
D = Dx =
- obszar normalny

względem osi OX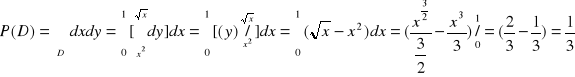

PRZYKŁAD 2:

Oblicz masę skupioną w obszarze D, który jest trójkątem o wierzchołkach (0,0), (0,1), (1,0) wiedząc, że gęstość masy jest określona wzorem f(x,y) = x + y

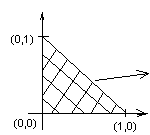
D = T

P(D) =

W tym przypadku D = T =

.

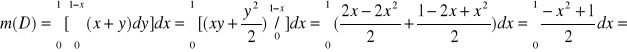
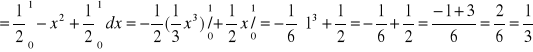
PRZYKŁAD 3:

Oblicz objętość bryły ograniczonej powierzchnią z = 1 - x² - y² i płaszczyzną XOY (z=0)

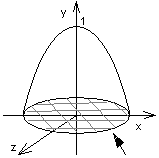
z = 1 - x² - y²

x² + y²
1 = K(r = 1) - koło domknięte

V =
,

gdzie D =
.

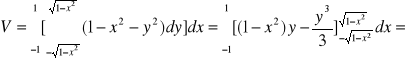
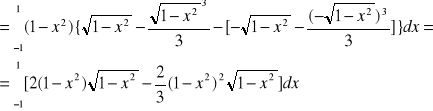
TWIERDZENIE 2 (zamiana zmiennych w całce podwójnej)

Niech funkcje:

(*)
określają pewne odwzorowanie T:

^(zbioru
)

przy czym
leży na płaszczyźnie
, a D na płaszczyźnie
.

Jeżeli:

1^o przekształcenie T określone (*) jest wzajemnie jednoznaczne oraz
(są ciągłe wraz z pierwszymi pochodnymi),

2^o funkcja f(x,y) jest ciągła w D tzn.
,

3^o jakobiem przekształcenia

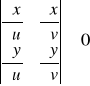
to

.

WNIOSEK 3 (współrzędne biegunowe):

Ponieważ

,

to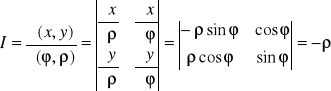
i

oraz

PRZYKŁAD 4:

Oblicz pole powierzchni z = 1 - x² - y² leżącej nad płaszczyzną z=0.

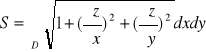
Tutaj D jest kołem określonym nierównością
tzn. jest obszarem normalnym względem osi OX, czyli

.

Ponieważ

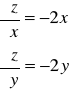
to

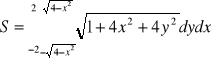
Zauważmy, że taka całka sprawia kłopoty rachunkowe w układzie kartezjańskim. Z tego względu wprowadźmy współrzędne biegunowe:

:

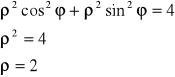
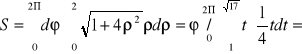
		2

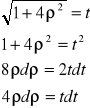
WNIOSEK 4:

Uogólnione współrzędne biegunowe (eliptyczne)

Wtedy

UWAGA:

Współrzędne biegunowe stosujemy przy podstawie kołowej, a uogólnione współrzędne biegunowe przy podstawie eliptycznej

II. CAŁKI KRZYWOLINIOWE

1. Całka krzywoliniowa nieskierowana

Całkę postaci
nazywamy całką krzywoliniową funkcji
określoną na łuku
.

Jeżeli
jest gęstością masy rozłożonej na łuku
, to całkowita masa skupioną na tym łuku wynosi:

Wszystkie podstawowe własności całki krzywoliniowej są podobne jak w przypadku całki pojedynczej.

TWIERDZENIE 3:

Niech łuk
jest określony parametrycznie:

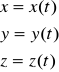
Jeżeli
jest gładki, tzn. że
,

^{(są ciągłe wraz z pochodnymi)}

to różniczka łuku wyraża się wzorem:

i

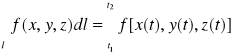
Jeżeli d(x, y, z) = d(stała)

to

, czyli

WNIOSEK 5:

Jeżeli łuk
leżący na płaszczyźnie jest określony w postaci parametrycznej

i
,

to

oraz

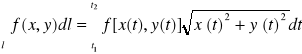
WNIOSEK 6:

Jeżeli łuk jest krzywą na płaszczyźnie określoną za pomocą funkcji:
,
, to

i

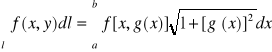
UWAGA:

Środek ciężkości łuku jednorodnego (d = stała gęstość) wyraża się wzorami:

= długość łuku jednorodnego.

PRZYKŁAD 5:

Oblicz środek ciężkości okręgu
[jednorodnego (d = constans)]

czyli

;

.

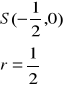
Korzystając z postaci parametrycznej okręgu

; w którym
,
;
,

równanie okręgu
; (
) przedstawimy następująco:

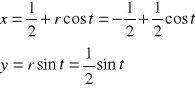
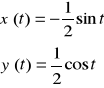
Wtedy

.

Zatem

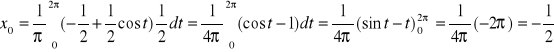
Podobnie

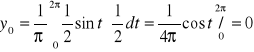
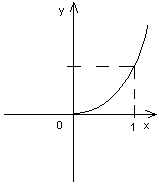
PRZYKŁAD 6:

Obliczyć masę linii niejednorodnej
określonej funkcją
,
, na której gęstość masy jest określona wzorem:

Ponieważ:

to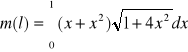

2. Całka krzywoliniowa skierowana

Rozważmy całkę krzywoliniową skierowaną w polu wektorowym

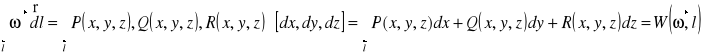
oznaczającą pracę W pola wektorowego
po łuku
.

Twierdzenie 1

Jeżeli pole wektorowe
jest ciągłe
na krzywej
regulowanej gładkiej skierowanej określonej parametrycznie:

,

to

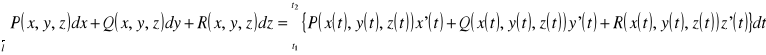
WNIOSEK

Jeżeli l jest łukiem regularnym, skierowanym, gładkim w
określonym parametrycznie:

x= x (t)
,

y= y (t)

to

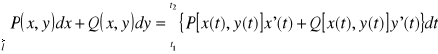
t

Uwagi:

Jeżeli l jest postaci y=y(x) dla x: a b,

to

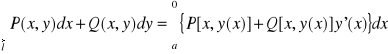
Jeżeli l jest określone w postaci x=x(y) , y: c d

to

dx=x'(y)dy

i

.

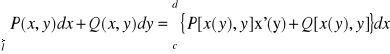
Tw. GREENA

Niech krzywa l jest zamknięta skierowana dodatnio (przeciwnie do wskazówek zegara), ograniczona obszarem płaskim D normalnym względem osi OX i OY i

C
(D) tzn., że
(x,y) i Q(x,y) są ciągłe wraz z pochodnymi cząstkowymi,

to

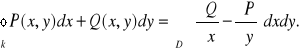
PRZYKŁAD 6

Obliczyć pracę siły
po okręgu o promieniu 1.

Równanie okręgu o promieniu r = 1 przyjmuje następujące postacie:

lub

Poszukiwaną pracę obliczamy wg wzoru

W =
=
.

1. Zamiana na całkę pojedynczą

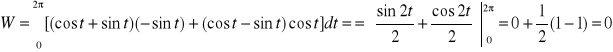
2. Zamiana na całkę podwójną( krzywa zamknięta)

WNIOSEK

Praca w polu wektorowym potencjalnym po krzywej zamkniętej wynosi zero tzn,

W = 0

Opracował:

Paweł Płóciniczak

[e-mail]

ZiM4

Poprawiali :

Agata Furmańczak ZiM1

Michał Drzewiecki ZiM1

Karolina Gańczak ZiM2

1

---