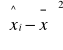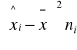Statystyka obejmuje metody zbierania, prezentacji i analizy danych dotyczących zjawisk masowych.
Zadaniem statystyki jest badanie prawidłowości zachodzących w zjawiskach masowych na podstawie badań.
Badanie statystyczne:
- planowanie badania
- obserwacja statystyczna
- opracowanie i prezentacja zebranego materiału statystycznego
- opis i wnioskowanie statystyczne
Planowanie badania - na etapie planowania badania należy określić:
- cel badania
- przedmiot badania
- zakres badania
Przedmiotem badania jest zawsze pewna zbiorowość statystyczna (populacja generalna).
Zbiorowością statystyczną nazywamy zbiór przedmiotów bądź osób (fizycznych bądź prawych) posiadających wiele cech wspólnych oraz przynajmniej jedną cechę pozwalającą rozróżnić elementy tego zbioru pomiędzy sobą.
Jednostką statystyczną nazywamy dowolny element zbiorowości statystycznej.
Przykład 1:
Celem badania jest diagnoza kondycji finansowej gospodarstw domowych w mieście Katowice za styczeń 2005 r.
Populacja: wszystkie gospodarstwa domowe w Katowicach
Jednostka statystyczna: jedna lub kilka osób prowadzących gospodarstwo domowe
Przykład 2:
Celem badania jest spędzanie wolnego czasu studentów GWSH w Katowicach za styczeń 2005 r.
Populacja: studenci GWSH w styczniu 2005 r.
Jednostka statystyczna: 1 osoba (1 student).
Wszystkie badania ze względu na zakres dzielimy na:
pełne
rejestracje
spisy
częściowe
próba statystyczna
Badanie nazywamy pełnym, jeżeli badaniu podlega cała populacja.
Rejestracja są to badania prowadzone w czasie ciągłym (na potrzeby zarządzania państwem).
Spisy są to badania, które prowadzone są okazjonalnie, mają ustaloną datę początku, czas trwania oraz datę końca (np. spisy powszechne, rolne, inwentażowe).
Badania częściowe są to badania, w których badaniu podlega wybrana część zbiorowości statystycznej, którą nazywamy próbą statystyczną.
Próba reprezentatywna - próbę nazywamy reprezentatywną, jeżeli struktura jednostek statystycznych w próbie odpowiada strukturze jednostek w populacji. Żeby poprawnie wybrać taką próbę należy znać wiedzę o populacji (poprzez powtarzanie zadania)
Obserwacja statystyczna:
cechy statystyczne, które będą podlegać badaniu
skale statystyczne służące uporządkowaniu wartości badanych cech statystycznych obserwowanych w próbie
należy zdecydować jaki będzie rodzaj ankiety
przeprowadzamy kontrolę zebranego materiału statystycznego
Cechy statystyczne:
stałe
rzeczowe (co?, kto?)
czasowe (kiedy przeprowadzamy badanie?)
przestrzenne (gdzie?)
zmienne
jakościowe - są to cechy, których wartości nie wyrażamy liczbowo () płeć, wykształcenie, miejsce zamieszkania, marka samochodu)
ilościowe - to takie, których wartość wyrażamy za pomocą liczb
skokowe - liczby całkowite (liczba osób prowadzących gospodarstwo domowe)
ciągłe - liczby rzeczywiste (dochód/osobę w gospodarstwie domowym)
Cechy stałe są to cechy, które nie podlegają badaniu. Służą identyfikacji jednostki statystycznej ze zbiorowością statystyczną.
Cechy zmienne są to cechy, które podlegają badaniu - mają zrealizować cel badania.
Skale statystyczne:
- nominalna (klasyfikacja) - służy do opisu wartości cech jakościowych, pozwala na klasyfikację wartości obserwowanej cechy na podzbiory, np. kolor żółty lub czerwony lub zielony
- porządkowa - wykorzystywana do cech jakościowych i ilościowych, mamy możliwość uporządkowania i klasyfikacji wartości badanych cech na podzbiory, np. wykształcenie, miejsce zamieszkania, porządek alfabetyczny, nazwy
- przedziałowa (interwałowa) - dotyczy cech ilościowych. Skala ma dwie charakterystyki:
brak stałego zera, przedziały mają ustaloną długość
- stosunkowa (proporcjonalna, ilorazowa) - zero absolutne, przedziały mają ustaloną długość
Brak stałego zera - zero ma pozycję umowną, np. skala temperaturowa.
W ankiecie mogą być pytania zamknięte (wybór jednej z podanych odpowiedzi), otwarte (należy wpisać odpowiedź) lub kombinacja tych podejść.
Kontrola:
- formalna - weryfikuje odpowiedzi dotyczące cech stałych
- merytoryczna - weryfikuje odpowiedzi dotyczące cech zmiennych - błędne odpowiedzi i brak odpowiedzi
Opracowanie i prezentacja zebranego materiału statystycznego
Zebrany materiał statystyczny można zaprezentować jako:
- szeregi statystyczne
- tablice statystyczne
- wykresy statystyczne
Szeregi statystyczne:
szczegółowe (wyliczające)
rozdzielcze (strukturalne)
cechy mierzalnej (ilościowej)
punktowe
przedziałowe
cechy niemierzalnej (jakościowe)
przestrzenne
czasowe
momentów
okresów
Każda prezentacja statystyczna powinna mieć:
- tytuł, w którym ujmujemy cechy stałe oraz cechę zmienną, która jest przedmiotem prezentacji (nad wykresem)
- źródło - podać pod spodem
Przykład:
Szereg wyliczający czasu dojazdu na zajęcia wybranej grupy studentów kierunku administracja GWSH w dniu 6.03.2005 r. (w min.)
Cechy wspólne: studenci kierunku administracja GWSH
23, 34, 45, 23, 34, 23, 45
Źródło: dane umowne
7 obserwacji
3 różne wartości
Rozdzielenie informacji dotyczących wartości badanej cechy oraz liczebności danej wartości.
xi |
yi |
23 |
3 |
34 |
2 |
45 |
2 |
xi - wartość obserwowanej cechy
yi - liczebność z jaką występuje kolejna wartość
n - liczba obserwacji
∑ - suma (sigma)
Jeżeli pojawia się subskrypt dolny „i” - będziemy mieli do czynienia z ciągiem, a jeśli subskryptu nie ma to będzie tylko 1 liczba
![]()
![]()
Szereg rozdzielczy przedziałowy
< |
ni |
4-6 |
12 |
6-8 |
10 |
8-10 |
8 |
10-12 |
6 |
Przedziały są lewostronnie domknięte, a prawostronnie otwarte, np. 6 należy do drugiego przedziału
![]()
Agregacja (grupowanie) danych - „zgubienie” pewnej informacji, nie można zmienić szeregu rozdzielczego przedziałowego w szereg wyliczający.
Szereg czasowy okresowy
ti |
yi |
1998 |
24 |
1999 |
25 |
2000 |
23 |
2001 |
22 |
2002 |
23 |
Szereg momentów - jeśli w pierwszej kolumnie są obserwacje dzienne.
Tablica statystyczna - jest to więcej niż jeden szereg statystyczny.
1. Poprawny dobór typu wykresów do informacji zawartych w szeregu bądź tablicy statystycznej.
2. Porównywalność wykresów między sobą - wykresy muszą być wykonane w tej samej skali.
Wykresy statystyczne:
- diagram
- wykres słupkowy
- histogram
- wielobok liczebności
- krzywa liczebności
Opis i wnioskowanie statystyczne
Opis statystyczny to analiza wartości badanych cech statystycznych obserwowanych w próbie statystycznej:
- analiza struktury zbiorowości
- analiza współzależności cech
- analiza zmian zjawisk w czasie
Wnioskowanie statystyczne - to przenoszenie wniosków badań z próby na populację statystyczną z wykorzystaniem rachunku prawdopodobieństwa.
Analiza struktury zbiorowości
Analiza statystyczna - przeprowadzana jest przy wykorzystaniu mierników i parametrów statystycznych.
Parametry statystyczne - są to liczby służące do opisu zbiorowości statystycznej.
Badanie prowadzimy z wykorzystaniem mierników które służą do oszacowania przybliżenia parametrów populacji.
Grupy mierników:
- miary poziomu przeciętnego
- miary zmienności
- miary asymetrii.
Miara poziomu przeciętnego:
- średnia arytmetyczna - podstawowy miernik do podziału średniej w szeregu wyliczającym
![]()
n - wielkość próby
![]()
- wartość badanej cechy w próbie
- średnia arytmetyczna ważona w szeregu rozdzielczym punktowym
xi |
ni |
x1 |
n1 |
... |
... |
xk |
nk |
![]()
k - liczba wartości cechy szeregu
ni - liczebność i-tej wartości cechy
n - suma liczebności ni
wagi = liczebności = ni
- średnia arytmetyczna ważona w szeregu rozdzielczym przedziałowym
![]()
n - suma liczebności ni
k - liczba klas (wierszy) w szeregu
![]()
- środek i-tego przedziału
ni - liczebność i-tego przedziału
Scharakteryzować zużycie energii w 168 gospodarstwach domowych na podstawie informacji <![]()
>
Zużycie energii (w kWh) |
Liczba gospodarstw domowych |
cum ni |
|
|
|
|
|
0-2 |
3 |
3 |
1 |
3 |
-6,8 |
46,24 |
138,72 |
2-4 |
12 |
15 |
3 |
36 |
-4,8 |
23,04 |
276,48 |
4-6 |
22 |
37 |
5 |
110 |
-2,8 |
7,84 |
172,48 |
6-8 |
48 |
85 |
7 |
336 |
-0,8 |
0,64 |
30,72 |
8-10 |
52 |
137 |
9 |
468 |
1,2 |
1,44 |
74,88 |
10-12 |
24 |
161 |
11 |
264 |
3,2 |
10,24 |
245,76 |
12-14 |
7 |
168 |
13 |
91 |
5,2 |
27,04 |
189,28 |
|
168 |
|
|
1308 |
|
|
1128,32 |
![]()
Miary poziomu przeciętnego (konsumpcyjne):
- dominanta
- kwartyle
Dominanta (moda, wartość modalna) - wartość cechy, która występuje w danej próbie najczęściej.
23, 34, 45, 23, 34, 23, 45
D=23
Dominanta ma w tym szeregu wartość 23.
xi |
ni |
2 |
8 |
3 |
10 |
4 |
5 |
5 |
2 |
D=3
xi |
ni |
2 |
3 |
3 |
5 |
4 |
2 |
5 |
5 |
D=3
D=5
Szereg dwumodalny - występują dwie dominanty.
Wyznaczamy przedział, w którym jest dominanta
Wyznaczamy dominantę wykorzystując wzór:
D ε <8;10)
![]()
k - k-ty przedział
xk - lewy koniec przedziału
∆xk - długość przedziału, w którym jest dominanta
nk - liczebność w przedziale dominanty
nk-1 - liczebność w przedziale poprzedzającym przedział dominanty
nk+1 - liczebność w przedziale następnym po przedziale dominanty
D= ![]()
W badanej próbie zużycie energii najczęściej wynosiło 825 kWh.
Mediana - wartość cechy, która dzieli próbę na 2 części, tak że połowa wartości jest nie większa oraz połowa wartości jest niemniejsza od mediany (wartość środkowa w próbie).
43, 56, 76, 84, 102 Me=(56+76)/2=66
Próba musi być uporządkowana
xi |
ni |
2 |
3 |
3 |
5 |
4 |
2 |
5 |
5 |
|
15 |
![]()
Szereg rozdzielczy przedziałowy:
wyznaczyć przedział, gdzie mieści się mediana
wyznaczyć wartość miernika wykorzystując wzór
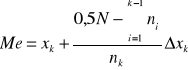
![]()
- suma liczebności w przedziałach od jeden (i=1) do przedziału poprzedzającego przedział (k-1), w którym jest mediana
Kwartyle dla szeregu rozdzielczego
Kwartyle - są to liczby, które dzielą uporządkowaną próbę na 4 części, w taki sposób, że ¼ wartości jest nie większa oraz ¾ wartości jest niemniejsza od mediany (wartość środkowa w próbie).
Q1=0,25
Q3=0,75
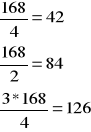
Q1=x42 <6;8)
Q2=x84 <6;8)
Q3=x126 <8;10)
![]()
W badanej próbie ½ gospodarstw domowych miała mnie3jsze zużycie energii nie przekraczające 6,2kWh.
![]()
Połowa badanych gospodarstw domowych miała zużycie energii nie przekraczające 2,96kWh.
![]()
25% badanych gospodarstw domowych miało zużycie energii przekraczające 9,58kWh.
2, 2, 3, 4
![]()
Me = 2
Miary zmienności (zróżnicowanie, rozproszenie, dywersyfikacja)
Badając zmienność wartości badanej cechy obserwujemy zmienność odległości od wartości przeciętnej. Im większe odchylenia tym większa zmienność wartości badanej cechy.
Wariancja - jest to średnia kwadratowa odchyleń wartości cechy od wartości przeciętnej.
Wariancja w szeregu rozdzielczym przedziałowym
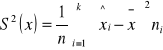
n - suma liczebności ni
k - liczba klas (wierszy) w szeregu
![]()
- środek i-tego przedziału
ni - liczebność i-tego przedziału
W szeregu punktowym nie występuje ^
W szeregu wyliczającym nie występuje ni
Wariancja jest miarą zmienności - im mniejsza wartość wariancji tym mniejsza zmienność badanej cechy.
Ze względu na trudną do interpretacji jednostkę z jaką wyznaczamy wariancję celem interpretacji obliczamy odchylenie standardowe jako:
![]()
Dla porównań zmienności cech statystycznych, które obserwowane są w różnych jednostkach nieporównywalnych wyznaczamy względną miarę względności i współczynnik zmienności.
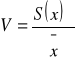
Liczba nieinterpretowana (bez jednostki), więc podajemy w %.
![]()
W badanej próbie przeciętne zużycie energii wyniosło 7,8 kWh z odchyleniem +/- 2,6kWh, czyli typowe zużycie energii w badanej próbie mieściło się w przedziale od (5,2; 10,4kWh).
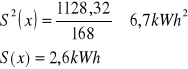
Asymetria rozkładu
Średnia większa od dominanty.
Asymetria prawostronna
Asymetria lewostronna
Rozkład symetryczny
Dla szeregu symetrycznego ![]()
Do pomiaru asymetrii rozkładu służy współczynnik skośności Persona
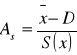
Współczynnik skośności jest miarą unormowaną. Wartości tego miernika należą do przedziału [-1; 1].
O znaku decyduje licznik, ponieważ S(x) jest zawsze dodatnie.
I Rozkład symetryczny
As=0
II Prawostronna asymetria
As>0
III Lewostronna asymetria
As<0
Jeżeli wartość bezwzględna współczynnika skośności rośnie do 1 wówczas rośnie siła asymetrii.
ANALIZA ZALEŻNOŚCI POMIĘDZY DWOMA CECHAMI STATYSTYCZNYMI
x |
y |
x1 x2 . . xn |
y1 y2 . . yn |
Zależność funkcjonalna - zmiana wartości jednej zmiennej powoduje ściśle określoną zmianę wartości drugiej zmiennej.
y = f(x)
Zależność funkcjonalna nie zawsze może być stosowana. Może być stosowana w momencie, kiedy znane są jakieś nadrzędne prawa, które pozwalają wyznaczyć tą zależność.
Zależność stochastyczna - wraz ze zmianą jednej zmiennej następuje zmiana rozkładu prawdopodobieństwa drugiej zmiennej.
Rozkład prawdopodobieństwa wyznaczamy wykorzystując wcześniejsze badania.
Przy zastosowaniu tego podejścia należy zadać pytanie o stabilność wyznaczonych rozkładów w czasie.
Zależność korelacyjna (statystyczna) - określonym wartością jednej zmiennej przyporządkowane są ściśle określone wartości średnie drugiej zmiennej.
Jest to podejście, które może być powszechnie stosowane.
Aby zbadać zależność korelacyjną miedzy dwoma cechami statystycznymi należy ustalić:
jaki jest rodzaj zależności korelacyjnej
jaka jest siła zależności korelacyjnej
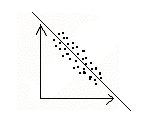
Odpowiadając na pytanie 1 wykonujemy wykres, który nazywa się wykres rozrzutu lub diagram korelacyjny.
Odpowiadając na pytanie 2 należy wyznaczyć odpowiedni miernik.
Kształt nie jest uzależniony od skali.
Zależność korelacyjna liniowa
Korelacja dodatnia - wraz ze wzrostem wartości jednej cechy następuje wzrost wartości drugiej cechy (zmiany są wprostproporcjonalne).
Korelacja ujemna - wzrostowi wartości jednej cechy odpowiada spadek wartości drugiej cechy (zmiany są odwrotnieproporcjonalne, tempo tych zmian nie musi być takie samo).
Badając siłę zależności liniowej korelacyjnej wyznaczamy współczynnik korelacji liniowej Pearsona przyjmujący wartości z przedziału [-1;1]
rxy = ![]()
= 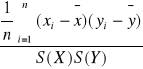
Licznik: iloraz kowariancji cech X i Y
Mianownik: iloczyn odchylenia standardowego cechy X i odchylenia standardowego cechy Y.
Przy analizie korelacji mamy symetrię. Obie zmienne oddziałowują na siebie tak samo.
S(x) = ![]()
>0
Odchylenie standardowe jest pierwiastkiem wariancji.
O znaku współczynnika w korelacji decyduje znak korelacji.
r = 1 Jeżeli punkty ułożą się na prostej o nachyleniu dodatnim
r = -1 Jeżeli punkty ułożą się na prostej o nachyleniu ujemnym
Przykład:
Zbadaj zależności między wydatkami na reklamę (x) oraz wielkością sprzedaży (y).
xi |
yi |
|
|
|
|
|
24 |
58 |
-13,4 |
-10,2 |
137,4 |
180,75 |
104,49 |
32 |
64 |
-5,4 |
-4,2 |
23,0 |
29,64 |
17,83 |
31 |
64 |
-6,4 |
-4,2 |
27,2 |
41,53 |
17,83 |
37 |
68 |
-0,4 |
-0,2 |
0,1 |
0,2 |
0,05 |
42 |
75 |
4,6 |
6,8 |
30,9 |
20,75 |
45,94 |
46 |
74 |
8,6 |
5,8 |
49,4 |
73,2 |
33,38 |
48 |
70 |
10,6 |
1,8 |
18,8 |
111,42 |
3,16 |
38 |
68 |
0,6 |
-0,2 |
-0,1 |
0,31 |
0,005 |
39 |
73 |
1,6 |
4,8 |
7,4 |
2,42 |
22,83 |
337 |
614 |
|
|
294,1 |
460,22 |
245,56 |
Wykonujemy wykres rozrzutu.
Wniosek: W badanej próbie zależność pomiędzy wielkością wydatków ma reklamę a wielkością sprzedaży jest korelacyjna liniowa dodatnia.
Siła zależności:
obliczmy wartości średnie badanych cech
![]()
37,4 zł
![]()
68,2 zł
W badanej próbie średnia wydatków na reklamę wynosi 37,4 zł.
odchylenia od średnich
(![]()
)
(![]()
)
kowariancja
cov (X,Y)=32,7
wariancja
S(x) = 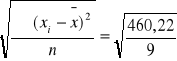
= 7,15
S(y) = 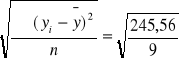
= 5,22
S(x)*S(y) = 34,35
współczynnik korelacji
Vxy =![]()
= 0,87
współczynnik determinacji - informuje w jakim stopniu zmiany wartości cechy x wyjaśniają zmiany wartości cechy y
d = r2 = 0,77
W badanej próbie zaobserwowano silną liniową zależność korelacyjną, co oznacza, że wraz ze wzrostem wydatków na reklamę rośnie wielkość sprzedaży. W badanej próbie poziom sprzedaży w 77% zależał od poziomu wydatków na reklamę, natomiast w pozostałych 23% zależał od innych czynników.
Współczynnik RANG
![]()
![]()
n - wielkość próby
Vx, Vy - rangi nadane wartościom badanych cech
Własności jak poprzednio omawiany miernik - stosowany tylko do liniowych.
Przykład:
Zbadaj zależność pomiędzy liczbą emitowanych reklam a wielkością obrotów wyznaczając współczynnik korelacji i rang.
L. reklam |
Wielkość obrotów |
Vx |
Vy |
Vx-Vy |
(Vx-Vy)2 |
3 |
115 |
1 |
1 |
0 |
0 |
5 |
133 |
3,5 |
2 |
1,5 |
2,25 |
4 |
142 |
2 |
3 |
-1 |
1 |
5 |
150 |
3,5 |
5 |
-1,5 |
2,25 |
6 |
148 |
5 |
4 |
1 |
1 |
7 |
151 |
6 |
6 |
0 |
0 |
|
|
|
|
|
6,5 |
n = 6
wykres rozrzutu
zależność dodatnia liniowa
rangi
![]()
![]()
= 0,814
współczynnik determinacji
d=0,662
W badanej próbie zaobserwowano silną liniową zależność korelacyjną dodatnią. Wielkość obrotów w 66,2% zależało od liczby emitowanych reklam.
Jeżeli badamy zależność korelacyjną pomiędzy:
- cechą jakościową i ilościową
- dwoma cechami jakościowymi
należy zastosować współczynnik rangowy.
Dane zagregowane (pogrupowane szeregi rozdzielcze) występują w postaci tablicy, która nazywa się tablicą korelacyjną.
X/Y |
y1 |
y2 |
∑ |
x1 x2 |
a c |
b d |
a+b c+d |
∑ |
a+d |
b+d |
n |
Sumy liczebności w wierszach oraz sumy liczebności w kolumnach są to liczebności brzegowe.
Współczynnik asocjacji Yulea Q
Q=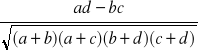
Własności jak w poprzednich miernikach.
Przykład:
W 500 rodzinach przeprowadzono obserwacje dotyczące koloru oczu ojca i syna.
|
Kolor oczu ojca |
|
|
Kolor oczu syna |
jasny |
ciemny |
∑ |
jasny |
30 |
80 |
110 |
ciemny |
170 |
220 |
390 |
∑ |
200 |
300 |
500 |
Q=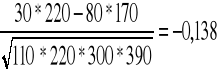
W badanej próbie zaobserwowano słabą zależność pomiędzy dziedziczeniem koloru oczu.
Tablica tychotomiczna - każda badana cecha ma tylko dwie wartości.
Analiza regresji
W analizie korelacji nie ma znaczenia, która zmienna została nazwana x, a która y.
Analiza regresji - pomiędzy badanymi cechami x i y przeprowadzamy, jeżeli pomiędzy badanymi cechami istnieje związek przyczynowo-skutkowy:
- badana cecha x ma wpływ na cechę y
- badana cecha y ma wpływ na cechę x
- badane cechy wpływają na siebie wzajemnie.
W przypadku zależności korelacyjnej liniowej przeprowadzając analizę regresji wyznaczamy liniowe funkcje regresji.
Funkcję regresji wyznaczamy posługując się metodą najmniejszych kwadratów.
Metoda najmniejszych kwadratów pozwala na wyznaczanie funkcji regresji tak, aby suma kwadratów odległości wartości empirycznych od wartości teoretycznych była minimalna.
zmienność ogólna = zmienność wyjaśniona regresją + zmienność resztowa
(![]()
) (![]()
![]()
) (![]()
)
Dla opisu wpływu zmian wartości cechy x na cechę y wyznaczamy w przypadku zależności liniowej funkcję regresji
![]()
wyznaczając minimum następującej funkcji:
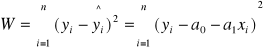
niewiadome: a1, a0
Niezależne współczynniki linii regresji (a1; a0) uzyskujemy rozwiązując układ równań normalnych.
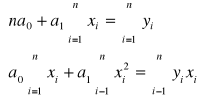
W wyznaczonym równaniu regresji interpretujemy wartość współczynnika a1, który informuje jak średnio zmienia się wartość cechy y, jeżeli cecha x rośnie o jedną jednostkę.
Dla opisu wpływu zmian wartości cechy y na zmiany wartości cechy x w przypadku zależności liniowej wyznaczamy równanie regresji
![]()
wyznaczając minimum następującej funkcji
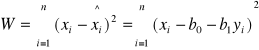
Niewiadome współczynniki równania regresji (b1, b0) wyznaczamy rozwiązując układ równań normalnych
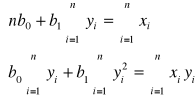
W wyznaczonym równaniu interpretujemy wartość współczynnika b1, który informuje jak średnio zmienia się wartość cechy x, jeżeli cecha y rośnie o jedną jednostkę.
a0, b0 - współczynniki przesunięcia, nie podlegają komentarzowi
a1, b1 - współczynniki kierunkowe linii regresji
Przykład:
Obliczanie parametrów funkcji regresji opisującej wpływ liczby zatrudnionych osób (x) na obroty w mln złotych (![]()
) w sklepach branży spożywczej.
|
|
xi2 |
xiyi |
yi2 |
|
|
23 |
149 |
529 |
3427 |
22201 |
160,9 |
141,61 |
4 |
35 |
16 |
140 |
1225 |
29,6 |
29,16 |
12 |
69 |
144 |
828 |
4761 |
84,9 |
|
3 |
33 |
9 |
99 |
1089 |
22,7 |
106,09 |
17 |
119 |
289 |
2023 |
14161 |
119,5 |
0,25 |
2 |
6 |
4 |
12 |
36 |
15,8 |
96,04 |
21 |
176 |
441 |
3696 |
30976 |
147,1 |
835,21 |
9 |
98 |
81 |
882 |
9604 |
62,2 |
1142,44 |
7 |
48 |
49 |
336 |
2304 |
50,4 |
5,76 |
12 |
47 |
144 |
564 |
2209 |
84,9 |
1436,41 |
110 |
780 |
1706 |
12007 |
88566 |
778 |
4045,78 |
wykres - zależność liniowa
które równanie? (X - Y czy Y - X)
X wpływa na Y
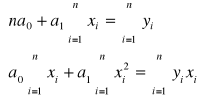
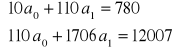
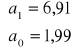
Równanie regresji ma postać: ![]()
Współczynnik regresji informuje, że wraz ze zwiększeniem zatrudnienia o 1 osobę wielkość obrotów rośnie średnio o 6,91 mln zł.
Przykład:
Obliczanie parametrów funkcji regresji opisującej wpływ wielkości obrotów w mln zł (![]()
) na liczbę zatrudnionych osób w sklepach branży spożywczej.
Y X
![]()
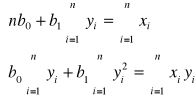
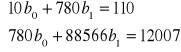
![]()
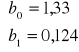
Równanie regresji ma postać: ![]()
Współczynnik regresji informuje, że zwiększenie obrotów o 10 mln zł powoduje zwiększenie zatrudnienia średnio o 1,24 osoby (1 osobę).
Równoważna metoda wyznaczania współczynników linii regresji
Współczynnik regresji informuje, ze wraz ze zwiększeniem zatrudnienia o 1 osobę wielkość obrotów rośnie średnio o 6,91 mln zł.
![]()
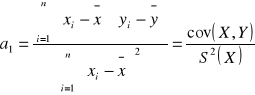
![]()
![]()
Związki pomiędzy współczynnikami regresji i współczynnikiem korelacji
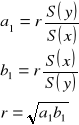
Współczynnik korelacji jest średnią geometryczną wyznaczoną ze współczynników kierunkowych linii regresji.
Jeżeli zmienne są niezależne wówczas linie regresji są prostopadłe.
Miary dopasowania linii regresji do danych empirycznych.
Trzy mierniki:
współczynnik determinacji (powinien być jak największy) r2
współczynnik zbieżności (powinien być jak najmniejszy) 1 - r2
wariancja resztowa
Współczynniki determinacji i zbieżności są miernikami symetrycznymi (wyrażone w %) i wyznaczane są dla obydwu linii regresji jednocześnie.
Wariancje resztowe:
- dla funkcji regresji y względem x wariancję resztową określamy wzorem:
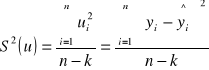
- dla funkcji regresji x względem y wariancję resztową określamy wzorem
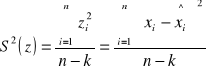
n - liczba elementów w próbie
k - liczba szacowanych elementów (dla funkcji liniowej k = 2)
S(u) [] taka jednostka jak cecha y
S(z) [] taka jednostka jak cecha x
Im mniejsza wartość wariancji resztowej tym lepsze dopasowanie linii regresji do danych.
![]()
mln zł
Oznacza to, że faktycznie zaobserwowane obroty w sklepach różnią się od szacowanego za pomocą funkcji regresji o 22,49 mln zł.
Analiza indeksowa szeregów czasowych
ti |
yi |
t1 |
y1 |
t2 |
y2 |
t3 |
y3 |
... |
... |
tn-1 |
yn-1 |
tn |
yn |
szereg dynamiczny
Proste metody badania zmian szeregu dynamicznego:
- przyrosty absolutne ∆
- przyrosty względne p
- wskaźniki dynamiki (indeksy) i
Przyrosty absolutne:
- ciąg przyrostów o podstawie stałej, za podstawę porównań przyjmujemy wielkość yk
y1-yk, y2-yk, y3-yk, ..., yn-1-yk, yn-yk
k=1,...,n
- ciąg przyrostów o podstawie łańcuchowej
y2-y1, y3-y2, y4-y3, ..., yn-1-yn-2, yn-yn-1
Ciąg przyrostów o podstawie stałej informuje o ile zmieniła się wartość badanej cechy w porównaniu z wartością yk.
Ciąg przyrostów o podstawie łańcuchowej informuje o ile zmieniła się wartość badanej cechy w porównaniu z wartością w okresie poprzednim.
Obydwie grupy mają jednostkę taką jak badana cecha.
Przyrosty względne:
- ciąg przyrostów o podstawie stałej, za podstawę porównań przyjmujemy wielkość yk
y1-yk / yk , y2-yk / yk, y3-yk / yk, ..., yn-1-yk / yk, yn-yk / yk
- ciąg przyrostów o podstawie łańcuchowej
y2-y1 / yk, y3-y2 / yk, y4-y3 / yk, ..., yn-1-yn-2 / yk, yn-yn-1 / yk
Ciąg przyrostów względnych o podstawie stałej informuje o ile zmieniła się wartość badanej cechy w stosunku do wartości yk.
Ciąg przyrostów względnych łańcuchowych informuje o ile zmieniła się wartość badanej cechy w stosunku do wartości w okresie poprzednim.
Dla interpretacji zamieniamy te liczby na procenty (ponieważ są liczbami niemianowanymi).
Wskaźniki dynamiki (indeksy):
- ciąg indeksów o podstawie stałej, za podstawę porównań przyjmujemy wielkość yk:
y1/yk, y2/yk, y3/yk ,..., yn-1/yk ,yn/yk
- ciąg indeksów o podstawie łańcuchowej
y2/y1, y3/y2, y4/y3, ..., yn-1/yn-2, yn/yn-1
Ciąg indeksów o podstawie stałej informuje ile razy wzrosła (zmalała) wartość badanej cechy w porównaniu z wartością yk.
Ciąg indeksów łańcuchowych informuje ile razy zmieniła się wartość badanej cechy w porównaniu z wartością w okresie poprzednim.
Indeksy są to mierniki niemianowane, które dla interpretacji zamieniamy na procenty.
Między dwoma ostatnimi grupami mamy następujące zależności:
indeks = przyrost względny + 1
i = p + 1
Przykład:
Ludność województwa śląskiego (w tys. osób)
|
|
|
|
|
|
|
|
1998 |
4882,4 |
0,0 |
- |
0 |
|
1 |
|
1999 |
4872,8 |
-9,7 |
-9,7 |
-0,002 |
-0,002 |
0,998 |
0,998 |
2000 |
4863,3 |
-19,1 |
-9,4 |
-0,004 |
-0,002 |
0,996 |
0,998 |
2001 |
4855,3 |
-27,1 |
-8,0 |
-0,006 |
-0,002 |
0,994 |
0,998 |
2002 |
4848,2 |
-34,3 |
-7,2 |
-0,007 |
-0,001 |
0,993 |
0,999 |
wyznaczyć przyrosty absolutne o podstawie stałej z roku 1998
k = 1998
W roku 2002 liczba mieszkańców w porównaniu z rokiem 1998 zmalała o 34,3 tys. osób.
wyznaczyć przyrosty absolutne łańcuchowe
W roku 2002 w porównaniu z rokiem 2001 nastąpił spadek liczby ludności o 7,2 tys. osób.
wyznaczyć przyrosty względne o podstawie stałej z roku 1998
W 2002 roku nastąpił spadek liczby ludności o 0,7% w porównaniu z rokiem 1998.
wyznaczyć przyrosty względne łańcuchowe
W roku 2002 nastąpił spadek liczby ludności w porównaniu z rokiem 2001 o 0,1%.
wyznaczyć indeksy o podstawie stałej z roku 1998
wyznaczyć indeksy łańcuchowe
Aby wyznaczyć średnia wartość badanego zjawiska w czasie należy wyznaczyć średnie tempo zmian, czyli średnią geometryczną obliczoną w ciągu indeksów łańcuchowych.
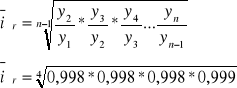
Agregatowe wskaźniki dynamiki dla wielkości absolutnych:
- zbiór produktów, towarów lub usług
q = [q1, q2, ..., ql]
Każda współrzędna tego wektora wyrażona jest w innej, nieporównywalnej bezpośrednio jednostce, np.: kg, zł
- wektor cen jednostkowych
p = [p1, p2, ..., pl]
- łączna wartość badanego zjawiska
![]()
Badanie prowadzimy w dwóch wybranych okresach czasu. Okres badany będziemy zapisywać „n”, okres podstawowy „o”. Badane okresy czasu mają jednostki porównywalne między sobą (2 lata, 2 miesiące, 2 kwartały).
Agregatowy indeks wartości informuje jak zmieniła się łączna wartość badanego zjawiska w okresie badanym w porównaniu z okresem podstawowym.
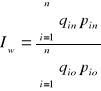
Przykład:
Wyznaczanie indeksów agregatowych charakteryzujących dynamikę produkcji wybranej grupy artykułów w marcu w porównaniu z lutym.
|
Miesięczna produkcja |
Cena jednostkowa w zł |
Wartość faktyczna w zł |
Wartość hipotetyczna w zł |
||||
|
qo |
qn |
po |
pn |
qopo |
qnpn |
qopn |
qnpo |
|
luty |
marzec |
luty |
marzec |
|
|
|
|
A[t] |
20 |
25 |
20 |
22 |
400 |
500 |
440 |
500 |
B[szt.] |
100 |
120 |
10 |
8 |
1000 |
960 |
800 |
1200 |
C[kg] |
360 |
300 |
8 |
9 |
2880 |
2700 |
3240 |
2400 |
∑ |
|
|
|
|
4280 |
4210 |
4480 |
4100 |
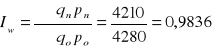
Łączna wartość trzech obserwowanych artykułów produkowanych w marcu zmalała o 1,64% w porównaniu z wartością produkcji w lutym.
Agregatowe indeksy ilości i cen - służą wyodrębnieniu wpływu ilości lub cen na zmianę wartości:
- formuła standaryzacyjna Paaschego polega na tym, że czynnik eliminowany stabilizujemy na poziomie okresu badanego (n)
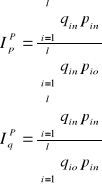
- formuła standaryzacyjna Laspeyresa - czynnik eliminowany stabilizujemy na poziomie okresu podstawowego
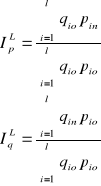
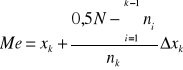
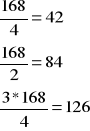
liczebność
x
D
ni
D x
ni
x
D
Zależność liniowa dodatnia
r>0
Brak zależności
(współczynnik korelacji w przybliżeniu wynosi 0)
Zależność nieliniowa
(nie wyznaczamy rxy)
Zależność liniowa ujemna
r<0
10 20 30 40 50
80
75
70
65
60
55
1 2 3 4 5 6 7
160
150
140
130
120
110
![]()
![]()
a>0
a<0
Zależność liniowa ujemna
Zależność liniowa dodatnia
![]()
![]()
![]()
![]()
![]()
Zmienność ogólna
Zmienność wyjaśniona regresją
Zmienność resztowa (niewyjaśniona regresją)
X Y
Y X
a0
b0
Stat. i dem. 1
Stat. i dem. 2
Stat. i dem. 3
Stat. i dem. 4
Stat. i dem. 5
Stat. i dem. 6
Stat. i dem. 7
Stat. i dem. 8
Stat. i dem. 9
Stat. i dem. 10
Stat. i dem. 11
Stat. i dem. 12
Wyszukiwarka