1. Metody określania ciśnienia statycznego górotworu.

1.1. Hipoteza sklepieniowa Cymbarewicza

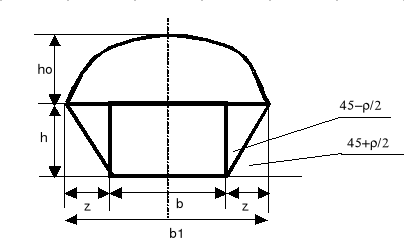
Hipoteza Cymbarewicza jest unowocześnioną hipotezą Protodiakonowa Cymbarewicza bierze pod uwagę niszczenie ociosów wyrobiska, które Protodiakonow traktował jako niezniszczalne. Według niego rozpiętość strefy odprężonej powstałej w warstwie stropowej wyrobiska poszerzają powstałe wzdłuż jego ociosów kliny odłamu. Skały położone w tym obszarze obciążają obudowę dając obciążenie w kierunku poziomym i pionowym. Obciążenie pionowe stanowi ciężar skał zawartych w wycinku paraboli, poziome zaś jest wynikiem zsuwania się skał wzdłuż założonej granicznej powierzchni ścięcia pod wpływem ciężaru warstw nadległych.

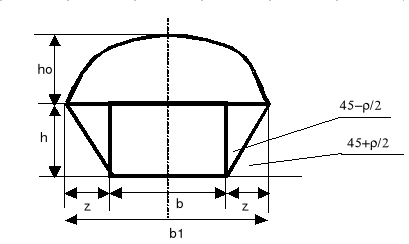
Rys. 5. Schemat dla modelu Cymbarewicza

Gdzie:

h-wysokość wyrobiska [m],

b-szerokość wyrobiska[m],

z-maksymalny zasięg zniszczenia [m]

Warunki :

• zachowanie stateczności ociosów,

• zachowanie stateczności sklepienia,

Zasięg zniszczenia oblicza się ze wzoru:

Zasięg strefy odprężonej oblicza się ze wzoru:

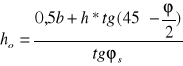
ϕ-pozorny kąt tarcia wewnętrznego skał ociosowych,

ϕs- pozorny kąt tarcia wewnętrznego skał w stropie

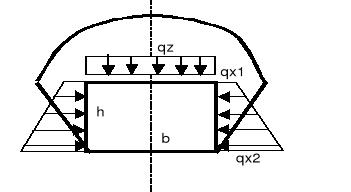
Rys.1. Schemat obciążeń wyrobiska:

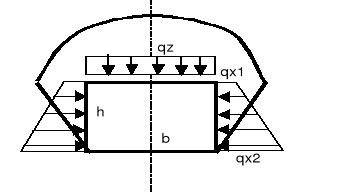
model cymbarewicza należy przyjmować dla wyrobisk zlokalizowanych w górotworze, w którym nad wyrobiskiem wytwarza się sklepienie odciążające,a ociosy nie przejmują w pełni ciężaru nadkładu, przy czym ciśnienie deformacyjne nie występuje lub jest praktycznie pomijane.

obciążenie pionowe: q_z=h_o*λ

obciążęnia poziome na krańcach ociosów:

q_x1=q_z*λ ,

q_x2=(q_z+h*γ_o)*λ ,

gdzie :

ho- zasięg strefy odprężonej [m],

γ- ciężar objętościowy [MN/m3],

h- wysokość wyrobiska w swietle włomu [m],

γo- średnia ciężaru objętościowego skał ociosowych [MN/m3],

ϕo-pozorny kąt tarcia wewnętrznego w ociosach [°],

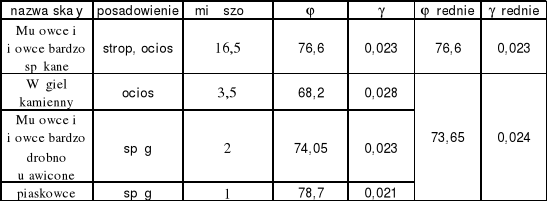
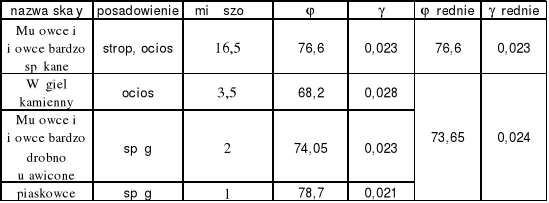
Tabela 14.Obliczenie parametrów średnich stropu i ociosów.

Wymiary wyrobiska:

b=5,5 m

h=4,0 m

Zasięg strefy odprężonej:

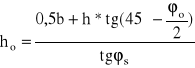
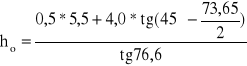
=0,8m

obciążenie pionowe: q_z=h_o*γ

γ=0,023 [MN/m³] z tabeli,(ciężar objętościowy skał stropowych).

q_z=h_o*γ=0,8*0,023=0,0182 [MN/m²]

Obciążenie poziome na krańcach ociosów :

Przy stropie:

λ=tg²(45-ϕ/2)=tg²(45-73,65/2)

λ=0,0206

q_z=0,0182 [MN/m²]

q_x1=q_z*λ=0,0182*0,0206=0,00037492 [Mpa]

dla spągu: q_x2=(q_z+h*γ_o)*λ

λ=0,0206

q_z=0,0182 [MN/m²]

h=4,0m,

γ_o=0,024 [MN/m³]

q_x2=(q_z+h*γ_o)*λ=(0,0182+4,0*0,024)*0,0206=0,00235252[Mpa]

Hipoteza sklepieniowa wyrobisk korytarzowych Cymbarewicza jest najlepsza spośród pozostałych, ponieważ autor uwzględnia zniszczenia nie tylko w stropie, ale również w ociosach wyrobiska. Cymbarewicz korzysta z doświadczeń Protodiakonowa, które wzbogaca i uzupełnia o swoje obserwacje poczynione w kopalniach bliższych czasom współczesnym. Uwzględnia większe głębokości posadowienia wyrobisk.

1.3. Zmodyfikowana hipoteza Sałustowicza.

Założeniem Sałustowicza było przyjęcie ośrodka sprężystego. Sałustowicz założył, że jeżeli w stropie lub spągu wyrobiska prostokątnego przekroczona zostanie wytrzymałość na rozciąganie która w tym ośrodku jest miarą zniszczenia, to wyrobisko samo będzie dążyć do przybrania przekroju eliptycznego, w którym maksymalne naprężenie rozciągające, nie przekracza wytrzymałości na rozciąganie. Nad stropem wyrobiska wytworzy się strefa odprężeniowa. Hipoteza ta jest bardzo ciekawa, ale modyfikacja Kłeczka ulepsza ją i uzupełnia. Kłeczek twierdzi, że ociosy się zniszczą. Płaszczyzny ścięcia pozostaną w ociosach pod kątem 45°-ϕ_oc/2 natomiast maksymalna strefa spękań w ociosach wynosi:

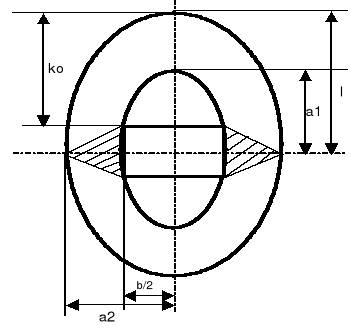
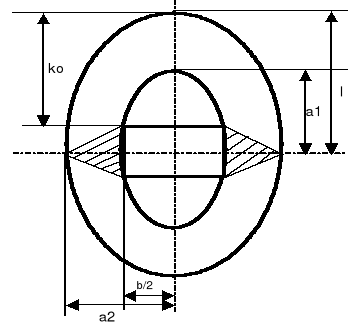
Rys.7. Schemat do hipotezy Sałstowicza

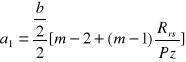
m - odwrotność liczby Poissona,

Rr- wytrzymałość na rozciąganie, [Mpa]

b,h- szerokość i wysokość wyrobiska, [m]

ϕ- pozorny kąt tarcia wewnętrznego, [°]

Pz- naprężenie pionowe pierwotne, [Mpa]

Dla warstwy mułowców i iłowców bardzo spękanych warstwa 26

ν=0,23

Rr=2,7 MPa,

Pz=16,42 MPa,

ϕ=76,6°

γ=0,023

m=4,34

b=5,5m

h=4,0m

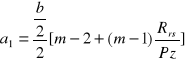
=1,375[4,34-2+3,34*2,7/16,42]=3,97m

=2,75+2*[tg45-76,6/2]=2,98m

=1,5[2,34+3,34*2,7/16,42]=3,33m

=3,33-2=1,33 m

1,33*0,023=0,03059 MPa

Obciążenie poziome na krańcach ociosów :

Przy stropie:

λ=tg²(45-ϕ/2)=tg²(45-76,6/2)

λ=0,0138

q_z=0,03059 [MN/m²]

q_x1=q_z*λ=0,03059*0,0138=0,000422142 [Mpa]

dla spągu: q_x2=(q_z+h*γ_o)*λ

λ=0,0138

q_z=0,03059 [MN/m²]

h=4,0m,

γ_o=0,023 [MN/m³]

q_x2=(q_z+h*γ_o)*λ=(0,03059+4,0*0,023)*0,0138=0,001691742[Mpa]

Analiza i wybór metody obliczeń

Do oceny obciążeń wybraliśmy hipotezę Cymbarewicza i Sałustowicza. Powołując się na Kłeczka, stwierdzono, że najbardziej zbliżone do rzeczywistości rezultaty uzyskuje się przy zastosowaniu hipotezy Cymbarewicza, jednak wyniki otrzymane w metodzie Sałustowicza są bardzo zbliżone:

Przy zastosowaniu hipotezy Cymbarewicza:

h_o=0,8 m

obciążenie pionowe:

q_z=0,0182 [MN/m²]

q_x1=0,00037492 [Mpa]

q_x2=0,00235252[Mpa]

Przy zastosowaniu hipotezy Sałustowicza:

h_o=1,33 m

obciążenie pionowe:

q_z=0,03059 [MN/m²]

q_x1= 0,000422142 [Mpa]

q_x2=0,001691742[Mpa]

---