§10. Szeregi potęgowe.

Dane są funkcje rzeczywiste f₁,f₂, ..................f określone na niepustym zbiorze ΩεR. Mówimy, że ciąg funkcyjny (f_n(x)), xεΩ, jest zbieżny punktowo do funkcji granicznej f jeżeli:
. Definicja: Mówimy, że ciąg funkcyjny (f₁(x)) xεΩ jest zbieżny jednostajnie względem xεΩ do funkcji granicznej f jeżeli

Definicja: Szereg funkcyjny
jest zbieżny punktowo do sumy f(x), xεΩ jeżeli
Szereg funkcyjny
, jest zbieżny jednostajnie do sumy f(x) xεΩ jeżeli ciąg sum częściowych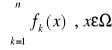
jest zbieżny jednostajnie względem xεΩ do f(x) tzn.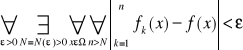

Twierdzenie 1. (Kryterium Weierstrassa)

Jeżeli dla szeregu funkcyjnego
zachodzą nierówności
dla każdego xεΩ oraz szereg liczbowy
jest zbieżny, to szereg
jest zbieżny jednostajnie względem xεΩ.

Szeregi funkcyjne postaci
gdzie a₀, xεR nazywamy szeregiem potęgowym.

Twierdzenie 2:

a) Jeżeli szereg
jest zbieżny, gdzie
to szereg potęgowy
jest zbieżny dla każdego x takiego, że |x|<|x₀| przy czym dla każdego ε ε(0,|x₀|) szereg ten jest zbieżny jednostajnie w zbiorze tych x, które spełniają nierówność

2. Jeżeli szereg
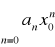
   jest rozbieżny to szereg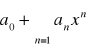
   jest rozbieżny dla x takich, że |x|>|x₀|Promieniem zbieżności szeregu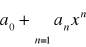
   nazywamy kres górny, czyli supremum R zbioru tych |x| dla których szereg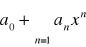
   jest zbieżny. Jeżeli zbiór ten jest nieograniczony, to przyjmujemy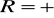
   . Przedział (skończony lub nieskończony) (-R,R) nazywamy przedziałem zbieżności szeregu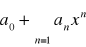
   o promieniu zbieżności R. Twierdzenie 3: (Twierdzenie Cauchyego -Hadamarda)

Niech
wtedy promień zbieżności szeregu
jest równy
gdy
przy czym gdy
przyjmujemy
gdy
przyjmujemy R=0.

Twierdzenie 4: Jeżeli
dla n=1,2,3,........ oraz ciąg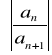
posiada granicę g (skończoną lub nieskończoną) to promień zbieżności szeregu
jest równy g. Jeżeli we wzorze Taylora
przyjąć x₀=0 ε ε<a,b>, to otrzymamy tzw. wzór Maclaurina w postaci

Twierdzenie 5: (O rozwijaniu funkcji w szereg Taylora lub szereg Maclaurina)

Jeżeli:funkcja f ma pochodne wszystkich rzędów w przedziale <a,b>

a)reszta w postaci Schlomilcha
dąży do zera przy
to dla x_0, x₀+h, ε <a,b> mamy

Jeżeli podstawimy h=x-x₀ to otrzymujemy
jest to tzw. szereg taylora dla funkcji f. W przypadku gdy x₀=0 otrzymujemy tzw. szereg Maclaurina w funkcji f

§ 11. WYZNACZANIE WYRAŻEŃ NIEOZNACZONYCH PRZY POMOCY POCHODNYCH.

WYRAŻENIA NIEOZNACZONE TYPU

TWIERDZENIE 1:

Jeżeli:

a)Funkcje f, g są określone na przedziale <a,b>

b)

c)istnieje skończona pochodna

to:
.

DOWÓD:Ponieważ istnieją skończone pochodne
więc funkcje f, g są ciągłe w x₀.

Zatem:

Ponieważ
więc ze wzoru, Taylora wynika, że istnieje taki otoczenie

Stąd dla
mamy: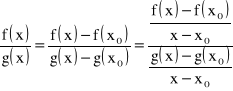
.

Przy
otrzymujemy:

Zachodzi również twierdzenie ogólniejsze:

TWIERDZENIE 2:

Jeżeli:

a)funkcje f, g są określone na przedziale <a,b>

b)

c)na przedziale <a,b> istnieje skończona pochodna
, przy czym

d)istnieje skończona pochodna

to: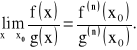

TWIERDZENIE 3:Jeżeli:funkcje f, g są określone na przedziale

1. 
   

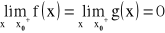
2. na przedziale
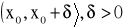
   istnieje skończona pochodna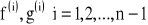
   , przy czym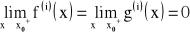
   

3. na przedziale
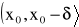
   istnieją skończone pochodne n-tego rzędu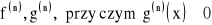
   oraz istnieje granica właściwa lub niewłaściwa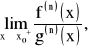
   

to: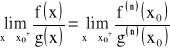
.

W twierdzeniu powyższym można również rozważać lewostronne otoczenie punktu x₀.

W przypadku, gdy
stosujemy:

TWIERDZENIE 4:

Jeżeli:

1. funkcje f, g są określone na przedziale
   

2. 
   
   

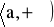
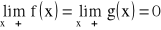
3. na przedziale
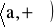
   istnieje skończona pochodna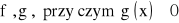
   oraz istnieje granica skończona lub nieskończona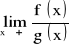
   ,

to:
. Do badania wyrażeń nieoznaczonych typu
stosujemy:

TWIERDZENIE 5:

Jeżeli:

1. funkcje f, g są określone na przedziale
   

2. 
   

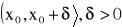
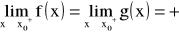
3. na przedziale
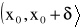
   istnieje skończona pochodna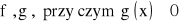
   oraz istnieje granica właściwa lub niewłaściwa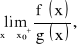
   

to:
.

Twierdzenie 5 można sformułować również w przypadku lewostronnego otoczenia x₀ oraz gdy
.

UWAGA!!!

Jeżeli funkcje f, g dążą do
, to zamiast badać wyrażenie typu
można badać wyrażenie typu
, pisząc tożsamość.

WYRAŻENIA NIEOZNACZONE TYPU

Wyrażenie typu
można sprowadzić do postaci
lub
pisząc tożsamość. Jeżeli
to można napisać :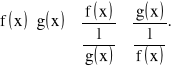

Jeżeli
, to badając wyrażenie
, można napisać tożsamość: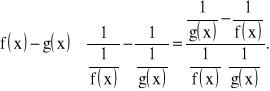

Jeżeli funkcja
jest przy
wyrażeniem nieoznaczonym typu
to (*) logarytmujemy obustronnie:
.

Jeżeli
, to
.

§ 12. CAŁKA NIEOZNACZONA

DEFINICJA:Funkcję F nazywamy funkcją pierwotną funkcji rzeczywistej f, określonej na przedziale otwartym (skończonym lub nieskończonym) X przyjmującej wartości rzeczywiste, jeżeli:

.

Jeżeli funkcja f jest określona na przedziale domkniętym<a,b>, to funkcję F nazywamy funkcją pierwotną funkcji f, jeżeli:

,

Niech C₁ oznacza dowolną stałą. Jeżeli F jest funkcją pierwotną funkcji f to zwg na to, że
, funkcja G, gdzie
, jest również funkcją pierwotną funkcji f.

Na odwrót, jeżeli
są funkcjami pierwotnymi funkcji f, to
, czyli na podstawie twierdzenia o wartości średniej:
, gdzie
jest odpowiednio dobraną stałą.

Zatem wyrażenie
, gdzie C jest dowolnie ustaloną stałą oraz
dla
jest ogólną postacią funkcji pierwotnej dla funkcji f.

DEFINICJA:Rodziną wszystkich funkcji pierwotnych funkcji f nazywamy całką nieoznaczoną z f i oznaczamy przy pomocy symbolu:
. Jeżeli funkcja f posiada całkę nieoznaczoną dla
, to mówimy, że f jest całkowalna dla
.

Zatem:
,

gdzie
dla każdego
, c-dowolne, ustalona stała. Wtedy funkcję f nazywamy funkcją podcałkową. Obliczanie całek nieoznaczonych nazywamy całkowaniem:

.

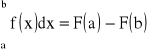
TWIERDZENIE 1:

Jeżeli funkcja f posiada funkcję pierwotną na przedziale (a,b) to dla każdego punktu
, gdzie
istnieje dokładnie jedna funkcja pierwotna F, taka, że:
.

TWIERDZENIE 2:

Jeżeli funkcja f jest ciągła na przedziale (a,b) to posiada na tym przedziale funkcje pierwotną.

TWIERDZENIE 3:

Jeżeli funkcje f, g są całkowalne dla
to:

, gdzie
-stałe.

DOWÓD:Ponieważ:

więc dla

UWAGA!:

Wzór z tezy twierdzenia 3 należy rozumieć następująco:

Dla dowolnych, ustalonych stałych c_f, c_g odpowiadających całkom:

, można dobrać stałą
odpowiadającą całce:
tak by zachodziła równość:
.

PODSTAWOWE METODY CAŁKOWANIA:

1. całkowanie przez podstawianie:

TWIERDZENIE 4:

Jeżeli:

1. funkcja f jest ciągła na przedziale (a,b)

2. funkcja
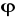
   ma ciągłą pochodną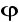
   na przedziale, (a,b)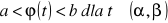
   
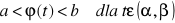
   to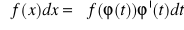
   gdzie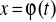
   dla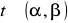
   

DOWÓD:

Niech:

Funkcja złożona
jest określona dla
. Z twierdzenia o pochodnej funkcji złożonej otrzymujemy:

(t)

.

Przyjmując
mamy:

.

2. całkowanie przez części („per partes”)

TWIERDZENIE 5:

Jeżeli funkcje
posiadają skończone pochodne
na przedziale (a,b) to dla każdego
zachodzi równość:

przy założeniu istnienia obu całek>

DOWÓD:Dla
zachodzi równość

,

stąd po obustronnym scałkowaniu otrzymujemy:

.

CAŁKI NIEOZNACZONE FUNKCJI ELEMENTARNEJ:

WZORY REKURENCYJNE:

1. 
   

2. 
   dla n=2,3,...

3. 
   

4.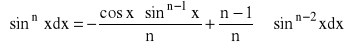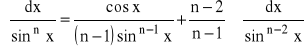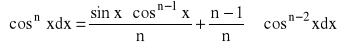 
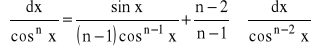
   dla n=2,3,...

CAŁKOWANIE FUNKCJI WYMIERNYCH:

Jeżeli funkcja podcałkowa jest funkcją wymierną tzn. ma postać
, gdzie P, Q są wielomianami algebraicznymi, to w przypadku, gdy stopień wielomianu P jest większy lub równy stopniowi wielomianu Q, wykonujemy dzielenie
. Otrzymujemy wielomian R(x) oraz resztę postaci
, przy czym stopień
jest większy niż stopień
.

Funkcją wymierną, dla której stopień licznika jest niższy od stopnia mianownika nazywamy ułamkiem właściwym.

Niech funkcja podcałkowa będzie ułamkiem właściwym
. Jeżeli wielomian Q ma pierwiastki rzeczywiste
odpowiednio rzędów
oraz pierwiastki zespolone
odpowiednio rzędów
to wielomian Q ma postać:

gdzie
jest liczbą sprzężoną do
.

Ponieważ:

,

gdzie
oraz

więc:

Funkcje wymierne postaci:

,
,

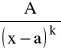
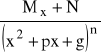
gdzie
nazywamy ułamkiem prostym.

TWIERDZENIE 6:

Każda funkcja wymierna
, gdzie stopień wielomianu P jest mniejszy niż stopień wielomianu Q oraz wielomian Q ma postać (1), rozkłada się jednoznacznie na sumę ułamków prostych:

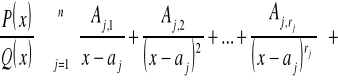
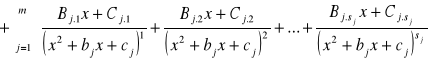
Całki ułamków prostych obliczamy w następujący sposób:

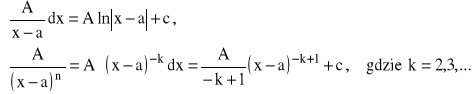
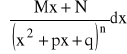
zakładamy, że

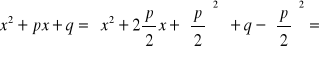
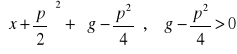
Podstawiamy:

Wtedy: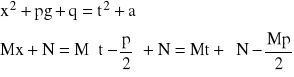

Zatem:

Podobnie podstawiając obliczamy całkę:

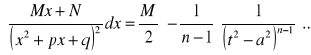
W dalszym ciągu stosujemy wzór rekurencyjny e):

.

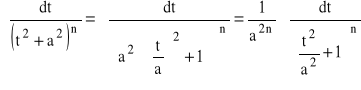
CAŁKOWANIE PEWNYCH FUNKCJI NIEWYMIERNYCH:

1. Podstawienia Eulera

Niech W=W(x,y) będzie funkcją wymierną dwóch zmiennych tzn.
, gdzie P, Q są wielomianami algebraicznymi zmiennych x, y.Rozważmy całkę:
.

Przy pomocy tzw. podstawień Eulera można zawsze sprowadzić wyrażenie:

do postaci funkcji wymiernej.

1. Jeżeli a>0 to podstawiamy:

lub

Wtedy otrzymujemy:

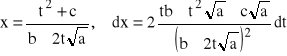
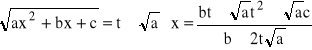
2. Jeżeli c>0 to podstawiamy:

wtedy:

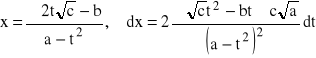
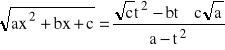
3. Jeżeli trójmian kwadratowy
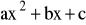
   posiada dwa różne pierwiastki x₁, x₂ tzn.:

to podstawiamy:

, gdzie i=1 lub i=2.

Wtedy np. przy i=1 otrzymujemy:

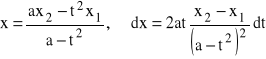
2. Niech
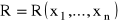
   będzie iloczynem sum skończonych postaci:

,

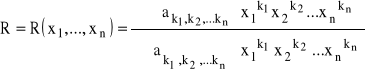
gdzie
-liczby całkowite nieujemne,

-stałe rzeczywiste.

1. Całkowanie wyrażeń:

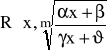
gdzie m-liczba naturalna, -stałe rzeczywiste.

Podstawiamy:

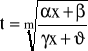
otrzymujemy: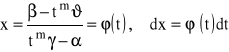

gdzie
jest funkcją wymierną.

W przypadku całki postaci:

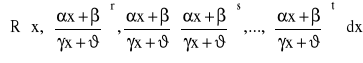
gdzie r,s,...t są liczbami dodatnimi. Wykładniki r,s,...,t sprowadzamy do wspólnego mianownika: m i podstawiamy:

.

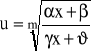
3. Całkowanie różniczek dwuwymiernych.

Różniczką dwuwymierną nazywamy wyrażenie:

gdzie m,n,p są liczbami wymiernymi
.

Całkę różniczki dwuwymiernej:

gdzie
,

można sprowadzić do całki z funkcji wymiernej wtedy, gdy co najmniej jedna z liczb:

jest całkowita.

1. Jeżeli p-liczba całkowita, to podstawiamy:

gdzie
najmniejsza wspólna wielokrotność mianowników liczb wymiernych m,n.

2. Jeżeli
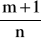
   -liczba całkowita, to podstawiamy:

gdzie
-mianownik liczby wymiernej p.

3. Jeżeli
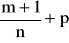
   -liczba całkowita, to podstawiamy:

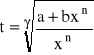
gdzie
mianownik liczby wymiernej p.

CAŁKOWANIE WYRAŻEŃ ZAWIERAJĄCYCH FUNKCJE TRYGONOMETRYCZNE:

1.Podstawienie uniwersalne:

a)Różniczka postaci:
,

gdzie funkcja dwóch zmiennych
jest

określona wcześniej, można sprowadzić do funkcji wymiernej stosując podstawienie

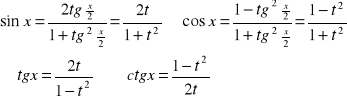
b)Jeżeli:

to podstawiamy:
.

Jeżeli:

to podstawiamy:
.

Jeżeli:

to podstawiamy:
.

c)Jeżeli wyrażenie podcałkowe ma postać:

gdzie
liczby wymierne
, to podstawiamy:
.

Wtedy:

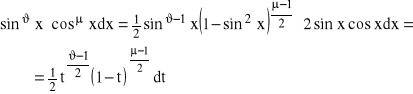
30

---