Wrocław, 15grudzień 2009
Politechnika Wrocławska
Laboratorium inżynierii bioreaktorów
Ćwiczenie 4: Rozkład czasu przybywania w reaktorach
Roksana Kowalik
Alicja Ulecka
Cel ćwiczenia:
Wyznaczenie rzeczywistego rozkładu czasu przebywania w kolumnie ze złożem upakowanym oraz w reaktorze mieszalnikowym i ich porównanie z modelem idealnym.
Dla przykładowych wartości obliczano kolejno:
a) Czas pobrania próbek ∆t [min] : ∆t= tn-t(n-1)
b) Objętościowe natężenie przepływu:
c) Średnie objętościowe natężenie przepływu:
śr =
d) przewodnośćλp [μS] : λp=λ.R
e) Ilość skł.A (na) [μS ml] : nA=λpVp ; n0A = ΣnA
na*∆t [μS ml min] : Σ na*.∆t
f) Funkcja rozkładu czasu przebywania: F(θ)=F(t) =
g) Średni czas bilansowy: τbilans =
h) Względny czas przebywania: θ =
i) Idealny rozkład czasu przebywania: Fid(t)=Fid(θ) =
j) Średni czas przebywania: τśr =
k) Całkowita objętość potrzebna do rozruchu reaktora: Vc =
l) Krotność wymiany: n =
Etap 1
Kolumna ze złożem upakowanym - metoda impulsowa
Metodyka: bezosobowa forma!!!!
1.Uruchomiłyśmy pompę. (uruchomiono pompę)
2.Zmierzyłyśmy strumień przepływu cieczy przez reaktor ze złożem upakowanym.
3.Jednorazowo wprowadziłyśmy na szczyt kolumny 0,5 ml 0,5 M roztworu KCl i uruchomiłyśmy stoper.
4.Pobierałyśmy próbki( po 2 ml, 5 ml), następnie notowałyśmy czas i przygotowywałyśmy rozcieńczenia (15x i 10x)
5.Na końcu mierzyłyśmy przewodność (konduktometrem ) na wyjściu z reaktora .
Opracowanie wyników:
Objętość , czas i rozcieńczenia próbek zestawiono w tabeli:
Lp próbek. |
Obj. Vp [ml] |
Czas trwania procesu t [min] |
Przeliczony czas procesu [min] |
Rozcieńczenie R |
1 |
2 |
0,59 |
0,98 |
15 |
2 |
2 |
2,16 |
2,27 |
15 |
3 |
2 |
3,36 |
3,60 |
15 |
4 |
2 |
4,52 |
4,87 |
15 |
5 |
2 |
6,17 |
6,28 |
15 |
6 |
2 |
7,38 |
7,63 |
15 |
7 |
2 |
9,08 |
9,13 |
15 |
8 |
2 |
10,36 |
10,60 |
15 |
9 |
2 |
12,08 |
12,13 |
15 |
10 |
2 |
13,36 |
13,60 |
15 |
11 |
2 |
15,15 |
15,25 |
15 |
12 |
2 |
16,5 |
16,08 |
15 |
13 |
2 |
18,35 |
18,58 |
15 |
14 |
2 |
20,12 |
20,20 |
15 |
15 |
2 |
22,01 |
22,02 |
15 |
16 |
5 |
26,17 |
26,28 |
10 |
17 |
5 |
30,57 |
30,95 |
10 |
18 |
5 |
35,4 |
35,07 |
10 |
19 |
5 |
38,31 |
38,52 |
10 |
v reaktora[ml]- 36 ml |
Dla kolumny ze złożem upakowanym obliczyłyśmy funkcję gęstości czasu przebywania E(t) oraz E(θ):
Gdzie:
E(Ө)= τ bilans E(t)
Lp. |
Czas pobrania próbek ∆t [min] |
Strumień [ml/min] |
Przewodność λp [μS] |
Przewodność Rzeczywista ( R*λp) [μS] |
Ilość skł.A nA [μSml] |
na*.∆t [μS ml min] |
E(t) |
E(θ) |
θ |
1 |
1,50 |
1,33 |
1,17 |
17,6 |
35 |
53 |
0,00108 |
0,0293 |
0,036 |
2 |
1,57 |
1,27 |
18 |
270,0 |
540 |
848 |
0,01669 |
0,4515 |
0,084 |
3 |
1,20 |
1,67 |
80 |
1200,0 |
2400 |
2880 |
0,07419 |
2,0067 |
0,133 |
4 |
1,16 |
1,72 |
98 |
1470,0 |
2940 |
3410 |
0,09088 |
2,4582 |
0,180 |
5 |
1,65 |
1,21 |
104 |
1560,0 |
3120 |
5148 |
0,09644 |
2,6087 |
0,232 |
6 |
1,21 |
1,65 |
96 |
1440,0 |
2880 |
3485 |
0,08902 |
2,4081 |
0,282 |
7 |
1,70 |
1,18 |
93 |
1395,0 |
2790 |
4743 |
0,08624 |
2,3328 |
0,338 |
8 |
1,28 |
1,56 |
75 |
1125,0 |
2250 |
2880 |
0,06955 |
1,8813 |
0,392 |
9 |
1,72 |
1,16 |
53 |
795,0 |
1590 |
2735 |
0,04915 |
1,3295 |
0,449 |
10 |
1,28 |
1,56 |
26 |
390,0 |
780 |
998 |
0,02411 |
0,6522 |
0,503 |
11 |
1,79 |
1,12 |
20 |
300,0 |
600 |
1074 |
0,01855 |
0,5017 |
0,564 |
12 |
1,35 |
1,48 |
12 |
180,0 |
360 |
486 |
0,01113 |
0,3010 |
0,595 |
13 |
1,85 |
1,08 |
8 |
120,0 |
240 |
444 |
0,00742 |
0,2007 |
0,687 |
14 |
1,77 |
1,13 |
6 |
90,0 |
180 |
319 |
0,00556 |
0,1505 |
0,747 |
15 |
1,89 |
1,06 |
4,5 |
67,5 |
135 |
255 |
0,00417 |
0,1129 |
0,814 |
16 |
4,16 |
1,20 |
4,5 |
45,0 |
225 |
936 |
0,00278 |
0,0753 |
0,972 |
17 |
4,40 |
1,14 |
4,5 |
45,0 |
225 |
990 |
0,00278 |
0,0753 |
1,144 |
18 |
4,83 |
1,04 |
2,7 |
27,0 |
135 |
652 |
0,00167 |
0,0452 |
1,296 |
19 |
2,91 |
1,72 |
2,05 |
20,5 |
103 |
298 |
0,00127 |
0,0343 |
1,424 |
Vc |
|
|
|
|
n0A |
ΣnA*∆t ._t |
τbilans |
τśr |
t max |
|
|
1,33 |
|
|
21528 |
32634 |
27,05 |
1,52 |
6,28 |
ułamek wprowadzonej masy znacznika przebywającej w aparacie w przedziale czasu ( t, t+ dt) E(t)
Charakter funkcji wyjścia pozwala ocenić stopień oddalenia od stanu idealnego przepływu. (?)
Zestawiając dwa wykresy t= f(nA) z obiczonym czasem bilansowym ( =27,05 jednoskta!!!)(?)
Podsumowanie:
→ idealny przepływ tłokowy z sygnałem impulsowym jest opisany zależnościami:
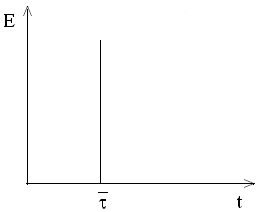
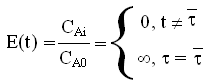
Na rysunkach przedstawiono funkcje na wejściu i odpowiedzi układu na wyjściu dla reaktora rurowego dla metody impulsowej:
- w reaktorze tłokowym barwnik pojawił się w strumieniu wyjściowym w postaci takiego samego sygnału, jak w wejściowym.
-przewodność wzrasta, pózniej opada. Możemy wnioskować , że układ dąży do osiągnięcia stanu stacjonarnego, w którym nie występuje zmiana stężeń składników w czasie.
-strumienie objętościowe zasilające i opuszczające układ reakcyjny muszą być sobie równe aby objętość układu pozostała niezmieniona.
-podczas przepływu tłokowego,warunkiem koniecznym i wystarczającym jest stwierdzenie, że czas przebywania w reaktorze wszystkich elementów płynu jest taki sam. Parametry płynu zmieniają się wzdłuż reaktora.
-rzeczywisty czas przebywania cząstek w reaktorze przepływowym zależy od charakteru przepływu. Przy przepływie tłokowym miałyśmy warunki rzeczywiste a nie idealne zatem wraz ze zmianą czasu przebywania składników w kolumnie stężenie cząstek zaczęło maleć( na wykresie zauważamy ten spadek).
-model przepływu tłokowego jest wyidealizowany i znacznie różni się od przepływu przebiegającego w warunkach rzeczywistych,gdzie nie ma tylko i wyłącznie przemieszania poprzecznego, ale występuje też w pewnym stopniu przemieszanie wzdłużne.
-t max=6,28 [min] w tym czasie, stężenie znacznika osiąga wartość maksymalną w przypadku rzeczywistym
Etap 2
Reaktor zbiornikowy - metoda skokowa (barwnik Acid Red 27, C=0.05 mg/ml)
Metodyka:
1.Zmierzyłyśmy absorbancję przygotowanego barwnika (Abs0) przy długości fali 523 nm.
2.Włączyłyśmy stoper w chwili rozpoczęcia dozowania barwnika lub wody (uruchomiłyśmy pompy).
3.Z wylotu reaktora pobierałyśmy frakcje o objętości 100 ml, każdorazowo mierząc strumień. 4.Pomiędzy frakcjami pobierałyśmy próbkę o objętości około 2 ml, mierzyłyśmy jej absorbancję na spektrofotometrze przy długości fali 523 nm wobec wody destylowanej jako kontroli.
Opracowanie wyników:
v reaktora [ml] |
370 |
abs0A |
1,463 |
Objętość , czas i absorbancję próbek zestawiono w tabeli:
Lp próbek. |
Obj. Vp [ml] |
Czas napełniania cylindra na 100ml ∆t [min] |
Czas trwania procesu t [min] |
Abs
λ=523 nm |
1 |
100 |
2,08 |
2,08 |
1,246 |
2 |
100 |
2,30 |
4,30 |
0,942 |
3 |
100 |
1,93 |
6,42 |
0,703 |
4 |
100 |
1,93 |
7,80 |
0,549 |
5 |
100 |
1,92 |
10,23 |
0,406 |
6 |
100 |
1,87 |
12,37 |
0,302 |
7 |
100 |
1,95 |
14,48 |
0,228 |
8 |
100 |
1,88 |
16,52 |
0,168 |
9 |
100 |
1,93 |
18,57 |
0,126 |
10 |
100 |
1,88 |
20,60 |
0,095 |
11 |
100 |
1,55 |
29,47 |
0,079 |
12 |
100 |
1,43 |
31,00 |
0,051 |
13 |
100 |
1,92 |
33,00 |
0,038 |
14 |
100 |
1,87 |
35,03 |
0,028 |
15 |
100 |
1,85 |
37,02 |
0,021 |
16 |
100 |
2,20 |
39,37 |
0,016 |
17 |
100 |
2,40 |
41,92 |
0,011 |
18 |
100 |
1,28 |
43,25 |
0,009 |
19 |
100 |
1,88 |
45,27 |
0,007 |
20 |
100 |
1,92 |
47,37 |
0,005 |
Z uzyskanych eksperymentalnie wyników obliczyłyśmy funkcję rozkładu czasu przebywania F(t) oraz F(θ):
Lp. |
Strumień [ml/min] |
F(θ)=F(t) |
θ |
Fid(t)=Fid(θ) |
τśr |
1 |
48,00 |
0,1483 |
-0,30 |
0,257 |
1,7459 |
2 |
43,48 |
0,3561 |
-0,61 |
0,455 |
1,4037 |
3 |
51,72 |
0,5195 |
-0,91 |
0,596 |
0,7496 |
4 |
51,72 |
0,6247 |
-1,09 |
0,662 |
0,5854 |
5 |
52,17 |
0,7225 |
-1,47 |
0,771 |
0,4301 |
6 |
53,57 |
0,7936 |
-1,77 |
0,830 |
0,3138 |
7 |
51,28 |
0,8442 |
-2,07 |
0,874 |
0,2447 |
8 |
53,10 |
0,8852 |
-2,37 |
0,906 |
0,1757 |
9 |
51,72 |
0,9139 |
-2,66 |
0,930 |
0,1344 |
10 |
53,10 |
0,9351 |
-2,96 |
0,948 |
0,0987 |
11 |
64,52 |
0,946 |
-4,25 |
0,986 |
0,0718 |
12 |
69,77 |
0,9651 |
-4,50 |
0,989 |
0,0439 |
13 |
52,17 |
0,974 |
-4,79 |
0,992 |
0,0403 |
14 |
53,57 |
0,9809 |
-5,08 |
0,994 |
0,0291 |
15 |
54,05 |
0,9856 |
-5,37 |
0,995 |
0,0217 |
16 |
45,45 |
0,9891 |
-5,69 |
0,997 |
0,0232 |
17 |
41,67 |
0,9925 |
-6,03 |
0,998 |
0,0168 |
18 |
77,92 |
0,9938 |
-6,26 |
0,998 |
0,0072 |
19 |
53,10 |
0,9952 |
-6,56 |
0,999 |
0,0073 |
20 |
52,17 |
0,9966 |
-6,86 |
0,999 |
0,0053 |
Vc |
|
τbilans |
τśr |
n |
|
2536 |
53,71 |
6,89 |
6,1486 |
6,86 |
|
Wykres F(t), Fid(t) = f(tp)
Podsumowanie:
Wykresy funkcji F(t) i E(t) dla reaktora z pełnym przemieszaniem z sygnałem skokowym w bardzo dużym stopniu przypominają wykresy F(t) i E(t) dla przepływów idealnych.
Wnioski
We wszystkich przypadkach udało się zmierzyć średni czas przebywania.
W reaktorach zbiornikowych rzeczywisty czas przebywania cząsteczek jest wielkością zmienna rozkładającą się według określonej funkcji statystycznej przy założeniach idealnych.
Druga metoda pod względem porównania średniego czasu przebywania cząstek w reaktorze z czasem bilansowym jest lepsza ponieważ wyniki są zbliżone. Zauważamy to na wykresie F(t), Fid(t) = f(tp), gdzie odchylenie od warunków idealnych jest nieznaczne.
Wyszukiwarka